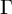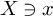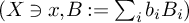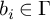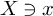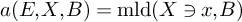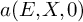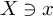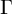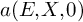1 Introduction
We work over an algebraically closed field of arbitrary characteristic.
The minimal log discrepancy (MLD) introduced by Vyacheslav Shokurov is an important invariant in birational geometry. Shokurov conjectured that the set of MLDs should satisfy the ascending chain condition (ACC) [Reference Shokurov18, Problem 5], and proved that the conjecture on termination of flips in the minimal model program (MMP) in characteristic
![]() $0$
follows from two conjectures on MLDs: the ACC conjecture for MLDs and the lower-semicontinuity conjecture for MLDs [Reference Shokurov21].
$0$
follows from two conjectures on MLDs: the ACC conjecture for MLDs and the lower-semicontinuity conjecture for MLDs [Reference Shokurov21].
The ACC conjecture for MLDs in dimension 2 was proved by Alexeev [Reference Alexeev1] and Shokurov [Reference Shokurov19] independently. We refer readers to [Reference Chen and Han5, Lemma 4.5, Theorems B.1 and B.4] and [Reference Han and Luo9, Theorem 1.5, Appendix A] for detailed proofs following Alexeev’s and Shokurov’s arguments, respectively, see also [Reference Chen, Gongyo and Nakamura6, Theorem 1.5]. The ACC conjecture for MLDs is still widely open in dimension 3 in general. We refer readers to [Reference Han, Liu and Shokurov8] and references therein for a brief history and related progress.
In order to study this conjecture for the case when
![]() $X\ni x$
is a fixed kawamata log terminal (klt) germ, Nakamura proposed conjecture 1.1. It is proved by Mustaţǎ-Nakamura [Reference Mustaţǎ and Nakamura17, Theorem 1.5] and Kawakita [Reference Kawakita13, Theorem 4.6] that Conjecture 1.1 is equivalent to the ACC conjecture for MLDs in this case.
$X\ni x$
is a fixed kawamata log terminal (klt) germ, Nakamura proposed conjecture 1.1. It is proved by Mustaţǎ-Nakamura [Reference Mustaţǎ and Nakamura17, Theorem 1.5] and Kawakita [Reference Kawakita13, Theorem 4.6] that Conjecture 1.1 is equivalent to the ACC conjecture for MLDs in this case.
Conjecture 1.1 ([Reference Mustaţǎ and Nakamura17, Conjecture 1.1])
Let
![]() ${\Gamma }\subseteq [0,1]$
be a finite set and
${\Gamma }\subseteq [0,1]$
be a finite set and
![]() $X\ni x$
a klt germ. Then there exists an integer N depending only on
$X\ni x$
a klt germ. Then there exists an integer N depending only on
![]() $X\ni x$
and
$X\ni x$
and
![]() ${\Gamma }$
satisfying the following.
${\Gamma }$
satisfying the following.
Let
![]() $(X\ni x,B)$
be an lc germ, such that
$(X\ni x,B)$
be an lc germ, such that
![]() $B\in {\Gamma }$
. Then there exists a prime divisor E over
$B\in {\Gamma }$
. Then there exists a prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
$a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
![]() $a(E,X,0)\le N.$
$a(E,X,0)\le N.$
When
![]() $\dim X=2$
, Conjecture 1.1 is proved by Mustaţǎ-Nakamura [Reference Mustaţǎ and Nakamura17, Theorem 1.3] in characteristic zero. Alexeev proved it when
$\dim X=2$
, Conjecture 1.1 is proved by Mustaţǎ-Nakamura [Reference Mustaţǎ and Nakamura17, Theorem 1.3] in characteristic zero. Alexeev proved it when
![]() ${\Gamma }$
satisfies the descending chain condition (DCC) [Reference Alexeev1, Lemma 3.7] as one of key steps in his proof of the ACC for MLDs for surfaces. See [Reference Chen and Han5, Theorem B.1] for a proof of Alexeev’s result in detail. Very recently, Ishii gave another proof of Conjecture 1.1 in dimension 2 [Reference Ishii11, Theorem 1.4] that works in any characteristic. Kawakita proved Conjecture 1.1 for the case when
${\Gamma }$
satisfies the descending chain condition (DCC) [Reference Alexeev1, Lemma 3.7] as one of key steps in his proof of the ACC for MLDs for surfaces. See [Reference Chen and Han5, Theorem B.1] for a proof of Alexeev’s result in detail. Very recently, Ishii gave another proof of Conjecture 1.1 in dimension 2 [Reference Ishii11, Theorem 1.4] that works in any characteristic. Kawakita proved Conjecture 1.1 for the case when
![]() $\dim X=3$
, X is smooth,
$\dim X=3$
, X is smooth,
![]() ${\Gamma }\subseteq \mathbb {Q}$
and
${\Gamma }\subseteq \mathbb {Q}$
and
![]() $(X\ni x,B)$
is canonical [Reference Kawakita13, Theorem 1.3] in characteristic zero.
$(X\ni x,B)$
is canonical [Reference Kawakita13, Theorem 1.3] in characteristic zero.
Naturally, one may ask whether Nakamura’s conjecture holds or not when
![]() $X\ni x$
is not necessarily fixed and
$X\ni x$
is not necessarily fixed and
![]() ${\Gamma }$
satisfies the DCC. If the answer is yes, not only the ACC conjecture for MLDs will hold for fixed germs
${\Gamma }$
satisfies the DCC. If the answer is yes, not only the ACC conjecture for MLDs will hold for fixed germs
![]() $X\ni x$
as we mentioned before, but also both the boundedness conjecture of MLDs and the ACC conjecture for MLDs for terminal threefolds
$X\ni x$
as we mentioned before, but also both the boundedness conjecture of MLDs and the ACC conjecture for MLDs for terminal threefolds
![]() $(X\ni x,B)$
will be immediate corollaries. One of main goals of this paper is to give a positive answer to this question in dimension 2.
$(X\ni x,B)$
will be immediate corollaries. One of main goals of this paper is to give a positive answer to this question in dimension 2.
Theorem 1.2. Let
![]() ${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC. Then there exists an integer N depending only on
${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC. Then there exists an integer N depending only on
![]() ${\Gamma }$
satisfying the following.
${\Gamma }$
satisfying the following.
Let
![]() $(X\ni x, B)$
be an lc surface germ, such that
$(X\ni x, B)$
be an lc surface germ, such that
![]() $B\in {\Gamma }$
. Then there exists a prime divisor E over
$B\in {\Gamma }$
. Then there exists a prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
$a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
![]() $a(E,X,0)\leq N$
.
$a(E,X,0)\leq N$
.
Theorem 1.2 implies that for any surface germ
![]() $(X\ni x,B)$
, such that
$(X\ni x,B)$
, such that
![]() $B\in {\Gamma }$
, there exists a prime divisor E, which could compute
$B\in {\Gamma }$
, there exists a prime divisor E, which could compute
![]() $\mathrm {mld}(X\ni x,B)$
and is ‘weakly bounded’, in the sense that
$\mathrm {mld}(X\ni x,B)$
and is ‘weakly bounded’, in the sense that
![]() $a(E,X,0)$
is uniformly bounded from above, among all divisorial valuations.
$a(E,X,0)$
is uniformly bounded from above, among all divisorial valuations.
A natural idea to prove Theorem 1.2 is to take the minimal resolution
![]() $\widetilde {f}:\widetilde {X}\to X$
, and apply Conjecture 1.1 in dimension 2. However, the coefficients of
$\widetilde {f}:\widetilde {X}\to X$
, and apply Conjecture 1.1 in dimension 2. However, the coefficients of
![]() $B_{\widetilde {X}}$
may not belong to a DCC set anymore, where
$B_{\widetilde {X}}$
may not belong to a DCC set anymore, where
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}:=\widetilde {f}^*(K_X+B)$
. In order to resolve this difficulty, we need to show Nakamura’s conjecture for the smooth surface germ, while the set of coefficients
$K_{\widetilde {X}}+B_{\widetilde {X}}:=\widetilde {f}^*(K_X+B)$
. In order to resolve this difficulty, we need to show Nakamura’s conjecture for the smooth surface germ, while the set of coefficients
![]() ${\Gamma }$
does not necessarily satisfy the DCC. It would be interesting to ask if similar approaches could be applied to solve some questions in birational geometry in high dimensions, that is, we solve these questions in a more general setting of coefficients on a terminalisation of X.
${\Gamma }$
does not necessarily satisfy the DCC. It would be interesting to ask if similar approaches could be applied to solve some questions in birational geometry in high dimensions, that is, we solve these questions in a more general setting of coefficients on a terminalisation of X.
Theorem 1.3. Let
![]() $\gamma \in (0,1]$
be a real number. Then
$\gamma \in (0,1]$
be a real number. Then
![]() $N_0:=\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
satisfies the following.
$N_0:=\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
satisfies the following.
Let
![]() $(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
$(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
![]() $X\ni x$
is smooth, and
$X\ni x$
is smooth, and
![]() $B_i$
are distinct prime divisors. Suppose that
$B_i$
are distinct prime divisors. Suppose that
![]() $\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Then there exists a prime divisor E over X, such that
$\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Then there exists a prime divisor E over X, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x,B)$
, and
$a(E,X,B)=\mathrm {mld}(X\ni x,B)$
, and
![]() $a(E,X,0)\leq 2^{N_0}$
.
$a(E,X,0)\leq 2^{N_0}$
.
We remark that for any DCC set
![]() ${\Gamma }$
, there exists a positive real number
${\Gamma }$
, there exists a positive real number
![]() $\gamma $
, such that
$\gamma $
, such that
![]() $\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0},b_i\in {\Gamma }\}\subseteq [\gamma ,+\infty )$
(see Lemma 2.2). However, the converse is not true. For example, the set
$\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0},b_i\in {\Gamma }\}\subseteq [\gamma ,+\infty )$
(see Lemma 2.2). However, the converse is not true. For example, the set
![]() ${\Gamma }:=[\frac {1}{2}+\frac {\gamma }{2},1]$
satisfies our assumption, but it is not a DCC set. It is also worthwhile to remark that all previous works we mentioned before did not give any effective bound even when
${\Gamma }:=[\frac {1}{2}+\frac {\gamma }{2},1]$
satisfies our assumption, but it is not a DCC set. It is also worthwhile to remark that all previous works we mentioned before did not give any effective bound even when
![]() ${\Gamma }$
is a finite set.
${\Gamma }$
is a finite set.
Theorem 1.3 indicates that there are some differences between Conjecture 1.1 and the ACC conjecture for MLDs, as the latter does not hold for such kind of sets.
When we strengthen the assumption ‘
![]() $\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
’ to ‘
$\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
’ to ‘
![]() $\{\sum _i n_ib_i-1\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
’, we may even give an explicit upper bound for
$\{\sum _i n_ib_i-1\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
’, we may even give an explicit upper bound for
![]() $a(E,X,0)$
for all prime divisors E over
$a(E,X,0)$
for all prime divisors E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $\mathrm {mld}(X\ni x,B)=a(E,X,B)$
. Theorem 1.4 is another main result in this paper.
$\mathrm {mld}(X\ni x,B)=a(E,X,B)$
. Theorem 1.4 is another main result in this paper.
Theorem 1.4. Let
![]() $\gamma \in (0,1]$
be a real number. Then
$\gamma \in (0,1]$
be a real number. Then
![]() $N_0:=\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
satisfies the following.
$N_0:=\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
satisfies the following.
Let
![]() $(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, such that
$(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, such that
![]() $X\ni x$
is smooth, where
$X\ni x$
is smooth, where
![]() $B_i$
are distinct prime divisors. Suppose that
$B_i$
are distinct prime divisors. Suppose that
![]() $\{\sum _i n_ib_i-1\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Then:
$\{\sum _i n_ib_i-1\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Then:
-
(1)
 $|S|\le N_0$
, where
$|S|\le N_0$
, where
 $S:=\{E\mid E\text { is a prime divisor over } X\ni x, a(E,X,B)=\mathrm {mld}(X\ni x,B)\}$
and
$S:=\{E\mid E\text { is a prime divisor over } X\ni x, a(E,X,B)=\mathrm {mld}(X\ni x,B)\}$
and -
(2)
 $a(E,X,0)\le 2^{N_0}$
for any
$a(E,X,0)\le 2^{N_0}$
for any
 $E\in S$
.
$E\in S$
.
Theorem 1.4 is a much deeper result than Theorem 1.3. To the best of the authors’ knowledge, such types of boundedness that result for
![]() $a(E,X,0)$
about all prime divisors which compute MLDs were never formulated in any literature before.
$a(E,X,0)$
about all prime divisors which compute MLDs were never formulated in any literature before.
We remark that
![]() ${\Gamma }:=[\frac {1}{2}+\frac {\gamma }{2},1)$
satisfies the assumption in Theorem 1.4, while
${\Gamma }:=[\frac {1}{2}+\frac {\gamma }{2},1)$
satisfies the assumption in Theorem 1.4, while
![]() ${\Gamma }:=[\frac {1}{2}+\frac {\gamma }{2},1]$
does not. It is clear that
${\Gamma }:=[\frac {1}{2}+\frac {\gamma }{2},1]$
does not. It is clear that
![]() $(\mathbf {A}^2,B_1+B_2)$
satisfies the assumptions in Theorem 1.3, but
$(\mathbf {A}^2,B_1+B_2)$
satisfies the assumptions in Theorem 1.3, but
![]() $|S|=+\infty $
, where
$|S|=+\infty $
, where
![]() $B_1$
and
$B_1$
and
![]() $B_2$
are defined by
$B_2$
are defined by
![]() $x=0$
and
$x=0$
and
![]() $y=0$
, respectively. For klt germs
$y=0$
, respectively. For klt germs
![]() $(X,B)$
, we always have
$(X,B)$
, we always have
![]() $|S|<+\infty $
. In this case, Example 3.3 shows that Theorem 1.3 does not hold for the set
$|S|<+\infty $
. In this case, Example 3.3 shows that Theorem 1.3 does not hold for the set
![]() ${\Gamma }:=\{\frac {1}{2}\}\cup \{\frac {1}{2}+\frac {1}{k+1}\mid k\in \mathbb {Z}_{\ge 0}\}$
, and Example 5.8 shows Theorem 1.4 may fail when
${\Gamma }:=\{\frac {1}{2}\}\cup \{\frac {1}{2}+\frac {1}{k+1}\mid k\in \mathbb {Z}_{\ge 0}\}$
, and Example 5.8 shows Theorem 1.4 may fail when
![]() $b_i=\frac {1}{2}$
for any i, that is why the equality for ‘
$b_i=\frac {1}{2}$
for any i, that is why the equality for ‘
![]() $\sum _i n_ib_i-1\geq 0$
’ is necessary. These examples also indicate that the assumptions in Theorems 1.3 and 1.4 might be optimal.
$\sum _i n_ib_i-1\geq 0$
’ is necessary. These examples also indicate that the assumptions in Theorems 1.3 and 1.4 might be optimal.
We also give an effective bound for Theorem 1.3 (respectively, Theorem 1.4) when
![]() $X\ni x$
is a fixed lc surface germ (respectively,
$X\ni x$
is a fixed lc surface germ (respectively,
![]() $X\ni x$
is a fixed klt surface germ), see Theorem 5.4 (respectively, Theorem 5.5).
$X\ni x$
is a fixed klt surface germ), see Theorem 5.4 (respectively, Theorem 5.5).
Postscript. Together with Jihao Liu, the authors proved the ACC for MLDs of terminal threefolds [Reference Han, Liu and Luo7, Theorem 1.1]. The proof is intertwined with Theorem 1.2 for terminal threefolds. Bingyi Chen informed the authors that he improved the upper bound
![]() $2^{N_0}$
given in Theorem 1.3 when the characteristic of the algebraically field is zero (see [Reference Chen4, Theorem 1.3]).
$2^{N_0}$
given in Theorem 1.3 when the characteristic of the algebraically field is zero (see [Reference Chen4, Theorem 1.3]).
2 Preliminaries
We adopt the standard notation and definitions in [Reference Kollár and Mori15], and will freely use them.
2.1 Arithmetic of sets
Definition 2.1 DCC and ACC sets
We say that
![]() ${\Gamma }\subseteq \mathbb {R}$
satisfies the DCC or
${\Gamma }\subseteq \mathbb {R}$
satisfies the DCC or
![]() ${\Gamma }$
is a DCC set if any decreasing sequence
${\Gamma }$
is a DCC set if any decreasing sequence
![]() $a_{1} \ge a_{2} \ge \cdots $
in
$a_{1} \ge a_{2} \ge \cdots $
in
![]() ${\Gamma }$
stabilises. We say that
${\Gamma }$
stabilises. We say that
![]() ${\Gamma }$
satisfies the ACC or
${\Gamma }$
satisfies the ACC or
![]() ${\Gamma }$
is an ACC set if any increasing sequence in
${\Gamma }$
is an ACC set if any increasing sequence in
![]() ${\Gamma }$
stabilises.
${\Gamma }$
stabilises.
Lemma 2.2. Let
![]() ${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC, and n a nonnegative integer. There exists a positive real number
${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC, and n a nonnegative integer. There exists a positive real number
![]() $\gamma $
which only depends on n and
$\gamma $
which only depends on n and
![]() ${\Gamma }$
, such that:
${\Gamma }$
, such that:
 $$ \begin{align*}\left\{\sum_i n_ib_i-n>0\mid b_i\in {\Gamma}, n_i\in \mathbb{Z}_{\geq 0}\right\}\subseteq [\gamma,+\infty).\end{align*} $$
$$ \begin{align*}\left\{\sum_i n_ib_i-n>0\mid b_i\in {\Gamma}, n_i\in \mathbb{Z}_{\geq 0}\right\}\subseteq [\gamma,+\infty).\end{align*} $$
Definition 2.3. Let
![]() $\epsilon \in \mathbb {R}, I\in \mathbb {R}\backslash \{0\}$
and
$\epsilon \in \mathbb {R}, I\in \mathbb {R}\backslash \{0\}$
and
![]() ${\Gamma }\subseteq \mathbb {R}$
be a set of real numbers. We define
${\Gamma }\subseteq \mathbb {R}$
be a set of real numbers. We define
![]() ${\Gamma }_\epsilon :=\cup _{b\in {\Gamma }} [b-\epsilon , b]$
and
${\Gamma }_\epsilon :=\cup _{b\in {\Gamma }} [b-\epsilon , b]$
and
![]() $\frac {1}{I}{\Gamma }:=\{\frac {b}{I}\mid b\in {\Gamma }\}$
.
$\frac {1}{I}{\Gamma }:=\{\frac {b}{I}\mid b\in {\Gamma }\}$
.
Lemma 2.4. Let
![]() ${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC. Then there exist positive real numbers
${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC. Then there exist positive real numbers
![]() $\epsilon ,\delta \leq 1$
, such that:
$\epsilon ,\delta \leq 1$
, such that:
 $$ \begin{align*}\left\{\sum_i n_ib_i'-1>0\mid b_i'\in {\Gamma}_{\epsilon}\cap[0,1], n_i\in \mathbb{Z}_{\geq 0}\right\}\subseteq [\delta,+\infty).\end{align*} $$
$$ \begin{align*}\left\{\sum_i n_ib_i'-1>0\mid b_i'\in {\Gamma}_{\epsilon}\cap[0,1], n_i\in \mathbb{Z}_{\geq 0}\right\}\subseteq [\delta,+\infty).\end{align*} $$
Proof. We may assume that
![]() ${\Gamma }\setminus \{0\}\neq \emptyset $
, otherwise we may take
${\Gamma }\setminus \{0\}\neq \emptyset $
, otherwise we may take
![]() $\epsilon =\delta =1$
.
$\epsilon =\delta =1$
.
Since
![]() ${\Gamma }$
satisfies the DCC, by Lemma 2.2, there exists a real number
${\Gamma }$
satisfies the DCC, by Lemma 2.2, there exists a real number
![]() $\gamma \in (0,1]$
, such that
$\gamma \in (0,1]$
, such that
![]() ${\Gamma }\setminus \{0\}\subseteq (\gamma ,1]$
, and
${\Gamma }\setminus \{0\}\subseteq (\gamma ,1]$
, and
![]() $\{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\ge 0}, b_i\in {\Gamma }\}\subseteq [\gamma , +\infty )$
. It suffices to prove that there exist
$\{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\ge 0}, b_i\in {\Gamma }\}\subseteq [\gamma , +\infty )$
. It suffices to prove that there exist
![]() $0<\epsilon ,\delta <\frac {\gamma }{2}$
, such that the set
$0<\epsilon ,\delta <\frac {\gamma }{2}$
, such that the set
![]() $\{\sum _i n_ib_i'-1\in (0,1]\mid b_i'\in {\Gamma }_{\epsilon }\cap [0,1], n_i\in \mathbb {Z}_{\geq 0}\}$
is bounded from below by
$\{\sum _i n_ib_i'-1\in (0,1]\mid b_i'\in {\Gamma }_{\epsilon }\cap [0,1], n_i\in \mathbb {Z}_{\geq 0}\}$
is bounded from below by
![]() $\delta $
, or equivalently:
$\delta $
, or equivalently:
 $$ \begin{align*}\left\{\sum_{i} n_ib_i'-1>0\mid b_i'\in {\Gamma}_{\epsilon}\cap[0,1], n_i\in \mathbb{Z}_{\ge0},\sum_{i} n_i\le \frac{4}{\gamma}\right\}\subseteq [\delta,+\infty).\end{align*} $$
$$ \begin{align*}\left\{\sum_{i} n_ib_i'-1>0\mid b_i'\in {\Gamma}_{\epsilon}\cap[0,1], n_i\in \mathbb{Z}_{\ge0},\sum_{i} n_i\le \frac{4}{\gamma}\right\}\subseteq [\delta,+\infty).\end{align*} $$
We claim that
![]() $\epsilon =\frac {\gamma ^2}{8}, \delta =\frac {\gamma }{2}$
have the desired property. Let
$\epsilon =\frac {\gamma ^2}{8}, \delta =\frac {\gamma }{2}$
have the desired property. Let
![]() $b_i'\in {\Gamma }_{\epsilon }\cap [0,1]$
and
$b_i'\in {\Gamma }_{\epsilon }\cap [0,1]$
and
![]() $n_i\in \mathbb {Z}_{\ge 0}$
, such that
$n_i\in \mathbb {Z}_{\ge 0}$
, such that
![]() $\sum _i n_ib_i'-1>0$
and
$\sum _i n_ib_i'-1>0$
and
![]() $\sum _{i} n_i\le \frac {4}{\gamma }$
. We may find
$\sum _{i} n_i\le \frac {4}{\gamma }$
. We may find
![]() $b_i\in {\Gamma }$
, such that
$b_i\in {\Gamma }$
, such that
![]() $0\le b_i-b_i'\leq \epsilon $
for any i. In particular,
$0\le b_i-b_i'\leq \epsilon $
for any i. In particular,
![]() $\sum _i n_ib_i-1>0$
. By the choice of
$\sum _i n_ib_i-1>0$
. By the choice of
![]() $\gamma $
,
$\gamma $
,
![]() $\sum _i n_ib_i-1\geq \gamma $
. Thus:
$\sum _i n_ib_i-1\geq \gamma $
. Thus:
 $$ \begin{align*}\sum_i n_ib_i'-1=\left(\sum_i n_ib_i-1\right)-\sum_i n_i(b_i-b_i') \geq \gamma-\frac{4}{\gamma}\epsilon=\frac{\gamma}{2}. \\[-42pt] \end{align*} $$
$$ \begin{align*}\sum_i n_ib_i'-1=\left(\sum_i n_ib_i-1\right)-\sum_i n_i(b_i-b_i') \geq \gamma-\frac{4}{\gamma}\epsilon=\frac{\gamma}{2}. \\[-42pt] \end{align*} $$
We will use the following lemma frequently without citing it in this paper.
Lemma 2.5. Let
![]() ${\Gamma }\subseteq [0,1]$
be a set, and
${\Gamma }\subseteq [0,1]$
be a set, and
![]() $\gamma \in (0,1]$
be a real number. If
$\gamma \in (0,1]$
be a real number. If
![]() $\{\sum _i n_ib_i-1>0\mid b_i\in {\Gamma }, n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma , +\infty )$
, then
$\{\sum _i n_ib_i-1>0\mid b_i\in {\Gamma }, n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma , +\infty )$
, then
![]() ${\Gamma }\setminus \{0\}\subseteq [\gamma ,1]$
.
${\Gamma }\setminus \{0\}\subseteq [\gamma ,1]$
.
Proof. Otherwise, we may find
![]() $b\in {\Gamma }$
, such that
$b\in {\Gamma }$
, such that
![]() $0<b<\gamma $
. Then
$0<b<\gamma $
. Then
![]() $0<(\lfloor \frac {1}{b}\rfloor +1)\cdot b-1\le b<\gamma $
, a contradiction.
$0<(\lfloor \frac {1}{b}\rfloor +1)\cdot b-1\le b<\gamma $
, a contradiction.
2.2 Singularities of pairs
Definition 2.6. A pair
![]() $(X,B)$
consists of a normal quasiprojective variety X and an
$(X,B)$
consists of a normal quasiprojective variety X and an
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $B\ge 0$
, such that
$B\ge 0$
, such that
![]() $K_X+B$
is
$K_X+B$
is
![]() $\mathbb {R}$
-Cartier. A germ
$\mathbb {R}$
-Cartier. A germ
![]() $(X\ni x, B:=\sum _i b_iB_i)$
consists of a pair
$(X\ni x, B:=\sum _i b_iB_i)$
consists of a pair
![]() $(X,B)$
, and a closed point
$(X,B)$
, and a closed point
![]() $x\in X$
, such that
$x\in X$
, such that
![]() $b_i>0$
, and
$b_i>0$
, and
![]() $B_i$
are distinct prime divisors on X with
$B_i$
are distinct prime divisors on X with
![]() $x\in \cap _i \operatorname {Supp} B_i$
. We call it a surface germ if
$x\in \cap _i \operatorname {Supp} B_i$
. We call it a surface germ if
![]() $\dim X=2$
.
$\dim X=2$
.
![]() $(X\ni x,B)$
is called an lc (respectively, klt, canonical, purely log terminal (plt), terminal) surface germ if
$(X\ni x,B)$
is called an lc (respectively, klt, canonical, purely log terminal (plt), terminal) surface germ if
![]() $(X\ni x,B)$
is a surface germ, and
$(X\ni x,B)$
is a surface germ, and
![]() $(X,B)$
is lc (respectively, klt, canonical, plt, terminal) near x.
$(X,B)$
is lc (respectively, klt, canonical, plt, terminal) near x.
Let
![]() $X\ni x$
be a germ. A birational morphism
$X\ni x$
be a germ. A birational morphism
![]() $f: Y\to X\ni x$
is a birational morphism from Y to X, such that all the exceptional divisors on Y are centered at x.
$f: Y\to X\ni x$
is a birational morphism from Y to X, such that all the exceptional divisors on Y are centered at x.
Definition 2.7. Let X be a normal quasiprojective surface and
![]() $x\in X$
a closed point. Then a birational morphism
$x\in X$
a closed point. Then a birational morphism
![]() $f: Y\to X$
(respectively,
$f: Y\to X$
(respectively,
![]() $f: Y\to X\ni x$
) is called a minimal resolution of X (respectively,
$f: Y\to X\ni x$
) is called a minimal resolution of X (respectively,
![]() $X\ni x$
) if Y is smooth (respectively, smooth over a neighborhood of
$X\ni x$
) if Y is smooth (respectively, smooth over a neighborhood of
![]() $x\in X$
) and there is no
$x\in X$
) and there is no
![]() $(-1)$
-curve on Y (respectively, over a neighborhood of
$(-1)$
-curve on Y (respectively, over a neighborhood of
![]() $x\in X$
).
$x\in X$
).
Note that the existence of resolutions of singularities for surfaces (see [Reference Lipman16]) and the minimal model program for surfaces (see [Reference Tanaka22] and [Reference Tanaka24]) are all known in positive characteristic. In particular, for any surface X (respectively, surface germ
![]() $X\ni x$
), we can construct a minimal resolution
$X\ni x$
), we can construct a minimal resolution
![]() $\tilde {f}: \widetilde {X}\to X$
(respectively,
$\tilde {f}: \widetilde {X}\to X$
(respectively,
![]() $\widetilde {f}: \widetilde {X} \to X\ni x$
).
$\widetilde {f}: \widetilde {X} \to X\ni x$
).
Definition 2.8. Let
![]() $(X\ni x,B)$
be an lc germ. We say a prime divisor E is over
$(X\ni x,B)$
be an lc germ. We say a prime divisor E is over
![]() $X\ni x$
if E is over X and
$X\ni x$
if E is over X and
![]() $\operatorname {center}_X E=x$
.
$\operatorname {center}_X E=x$
.
The minimal log discrepancy of
![]() $(X\ni x,B)$
is defined as:
$(X\ni x,B)$
is defined as:
Let
![]() $f:Y\to X$
be a projective birational morphism, we denote it by
$f:Y\to X$
be a projective birational morphism, we denote it by
![]() $f: Y\to X\ni x$
if
$f: Y\to X\ni x$
if
![]() $\operatorname {center}_{X}E=x$
for any f-exceptional divisor E.
$\operatorname {center}_{X}E=x$
for any f-exceptional divisor E.
Let
![]() $\widetilde {f}: \widetilde {X} \to X\ni x$
be the minimal resolution of
$\widetilde {f}: \widetilde {X} \to X\ni x$
be the minimal resolution of
![]() $X\ni x$
, and we may write
$X\ni x$
, and we may write
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}+\sum _{i} (1-a_i)E_i= \widetilde {f}^{*}(K_{X}+B),$
where
$K_{\widetilde {X}}+B_{\widetilde {X}}+\sum _{i} (1-a_i)E_i= \widetilde {f}^{*}(K_{X}+B),$
where
![]() $B_{\widetilde {X}}$
is the strict transform of B,
$B_{\widetilde {X}}$
is the strict transform of B,
![]() $E_i$
are
$E_i$
are
![]() $\widetilde {f}$
-exceptional prime divisors and
$\widetilde {f}$
-exceptional prime divisors and
![]() $a_i:=a(E_i,X,B)$
for all i. The partial log discrepancy (PLD) of
$a_i:=a(E_i,X,B)$
for all i. The partial log discrepancy (PLD) of
![]() $(X\ni x,B)$
,
$(X\ni x,B)$
,
![]() $\operatorname {pld}(X\ni x,B)$
, is defined as follows.
$\operatorname {pld}(X\ni x,B)$
, is defined as follows.
 $$ \begin{align*}\operatorname{pld}(X\ni x,B):=\left\{ \begin{array}{lcl} \min_{i}\{a_i\} &{\text{if }x\in X \text{ is a singular point,}}\\ +\infty &{\text{if } x\in X \text{ is a smooth point.}} \end{array} \right.\end{align*} $$
$$ \begin{align*}\operatorname{pld}(X\ni x,B):=\left\{ \begin{array}{lcl} \min_{i}\{a_i\} &{\text{if }x\in X \text{ is a singular point,}}\\ +\infty &{\text{if } x\in X \text{ is a smooth point.}} \end{array} \right.\end{align*} $$
The following result is known as the ACC for PLDs (for surfaces).
Theorem 2.9 ([Reference Alexeev1, Theorem 3.2],[Reference Han and Luo9, Theorem 2.2])
Let
![]() ${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC. Then:
${\Gamma }\subseteq [0,1]$
be a set which satisfies the DCC. Then:
satisfies the ACC.
2.3 Dual graphs
Definition 2.10 (c.f. [Reference Kollár and Mori15, Definition 4.6])
Let
![]() $C=\cup _i C_i$
be a collection of proper curves on a smooth surface U. We define the dual graph
$C=\cup _i C_i$
be a collection of proper curves on a smooth surface U. We define the dual graph
![]() ${\mathcal {DG}}$
of C as follows.
${\mathcal {DG}}$
of C as follows.
-
(1) The vertices of
 ${\mathcal {DG}}$
are the curves
${\mathcal {DG}}$
are the curves
 $C_j$
.
$C_j$
. -
(2) Each vertex is labelled by the negative self intersection of the corresponding curve on U, we call it the weight of the vertex (curve).
-
(3) The vertices
 $C_i,C_j$
are connected with
$C_i,C_j$
are connected with
 $C_i\cdot C_j$
edges.
$C_i\cdot C_j$
edges.
Let
![]() $f: Y\to X\ni x$
be a projective birational morphism with exceptional divisors
$f: Y\to X\ni x$
be a projective birational morphism with exceptional divisors
![]() $\{E_i\}_{1\leq i\leq m}$
, such that Y is smooth. Then the dual graph
$\{E_i\}_{1\leq i\leq m}$
, such that Y is smooth. Then the dual graph
![]() ${\mathcal {DG}}$
of f is defined as the dual graph of
${\mathcal {DG}}$
of f is defined as the dual graph of
![]() $E=\cup _{1\leq i\leq m} E_i$
. In particular,
$E=\cup _{1\leq i\leq m} E_i$
. In particular,
![]() ${\mathcal {DG}}$
is a connected graph.
${\mathcal {DG}}$
is a connected graph.
Definition 2.11. A cycle is a graph whose vertices and edges can be ordered
![]() $v_1,\ldots ,v_m$
and
$v_1,\ldots ,v_m$
and
![]() $e_1,\ldots ,e_m (m\ge 2)$
, such that
$e_1,\ldots ,e_m (m\ge 2)$
, such that
![]() $e_i$
connects
$e_i$
connects
![]() $v_i$
and
$v_i$
and
![]() $v_{i+1}$
for
$v_{i+1}$
for
![]() $1\leq i\leq m$
, where
$1\leq i\leq m$
, where
![]() $v_{m+1}=v_1$
.
$v_{m+1}=v_1$
.
Let
![]() ${\mathcal {DG}}$
be a dual graph with vertices
${\mathcal {DG}}$
be a dual graph with vertices
![]() $\{C_i\}_{1\leq i\leq m}$
. We call
$\{C_i\}_{1\leq i\leq m}$
. We call
![]() ${\mathcal {DG}}$
a tree if:
${\mathcal {DG}}$
a tree if:
-
(1)
 ${\mathcal {DG}}$
does not contain a subgraph which is a cycle and
${\mathcal {DG}}$
does not contain a subgraph which is a cycle and -
(2)
 $C_i\cdot C_j\leq 1$
for all
$C_i\cdot C_j\leq 1$
for all
 $1\leq i\neq j\leq m$
.
$1\leq i\neq j\leq m$
.
Moreover, if C is a vertex of
![]() ${\mathcal {DG}}$
that is adjacent to more than three vertices, then we call C a fork of
${\mathcal {DG}}$
that is adjacent to more than three vertices, then we call C a fork of
![]() ${\mathcal {DG}}$
. If
${\mathcal {DG}}$
. If
![]() ${\mathcal {DG}}$
contains no fork, then we call it a chain.
${\mathcal {DG}}$
contains no fork, then we call it a chain.
Lemma 2.12. Let
![]() $X\ni x$
be a surface germ. Let
$X\ni x$
be a surface germ. Let
![]() $Y,Y'$
be smooth surfaces, and let
$Y,Y'$
be smooth surfaces, and let
![]() $f: Y\to X\ni x$
and
$f: Y\to X\ni x$
and
![]() $f':Y'\to X\ni x$
be two projective birational morphisms, such that
$f':Y'\to X\ni x$
be two projective birational morphisms, such that
![]() $f'$
factors through f. If the dual graph of f is a tree whose vertices are all smooth rational curves, then the dual graph of
$f'$
factors through f. If the dual graph of f is a tree whose vertices are all smooth rational curves, then the dual graph of
![]() $f'$
is a tree whose vertices are all smooth rational curves.
$f'$
is a tree whose vertices are all smooth rational curves.
Proof. Let
![]() $g: Y'\to Y$
be the projective birational morphism, such that
$g: Y'\to Y$
be the projective birational morphism, such that
![]() $f\circ g=f'$
. Since g is a composition of blow-ups at smooth closed points, by induction on the number of blow-ups, we may assume that g is a single blow-up of Y at a smooth closed point
$f\circ g=f'$
. Since g is a composition of blow-ups at smooth closed points, by induction on the number of blow-ups, we may assume that g is a single blow-up of Y at a smooth closed point
![]() $y\in Y$
.
$y\in Y$
.
Let
![]() $E'$
be the g-exceptional divisor on
$E'$
be the g-exceptional divisor on
![]() $Y'$
,
$Y'$
,
![]() $\{E_i\}_{1\leq i\leq m}$
the set of distinct exceptional curves of f on Y and
$\{E_i\}_{1\leq i\leq m}$
the set of distinct exceptional curves of f on Y and
![]() $\{E_i'\}_{1\leq i\leq m}$
their strict transforms on
$\{E_i'\}_{1\leq i\leq m}$
their strict transforms on
![]() $Y'$
. By assumption,
$Y'$
. By assumption,
![]() $E_i'\cdot E_j'\leq g^{*}E_i\cdot E_j'=E_i\cdot E_j\leq 1$
for
$E_i'\cdot E_j'\leq g^{*}E_i\cdot E_j'=E_i\cdot E_j\leq 1$
for
![]() $1\leq i\neq j\leq m$
. Since
$1\leq i\neq j\leq m$
. Since
![]() $E_i$
is smooth,
$E_i$
is smooth,
![]() $0=g^{*}E_i\cdot E'\ge (E_i'+E')\cdot E'$
. It follows that
$0=g^{*}E_i\cdot E'\ge (E_i'+E')\cdot E'$
. It follows that
![]() $E'\cdot E_i'\leq 1$
for
$E'\cdot E_i'\leq 1$
for
![]() $1\leq i\leq m$
.
$1\leq i\leq m$
.
If the dual graph of
![]() $f'$
contains a cycle, then
$f'$
contains a cycle, then
![]() $E'$
must be a vertex of this cycle. Let
$E'$
must be a vertex of this cycle. Let
![]() $E',E_{i_1}',\ldots ,E_{i_k}'$
be the vertices of this cycle,
$E',E_{i_1}',\ldots ,E_{i_k}'$
be the vertices of this cycle,
![]() $1\leq k\leq m$
. Then the vertex-induced subgraph by
$1\leq k\leq m$
. Then the vertex-induced subgraph by
![]() $E_{i_1},\ldots ,E_{i_k}$
of the dual graph of f is a cycle, a contradiction.
$E_{i_1},\ldots ,E_{i_k}$
of the dual graph of f is a cycle, a contradiction.
The following lemma maybe well known to experts (c.f. [Reference Chen and Han5, Lemma 4.2]). For the reader’s convenience, we include the proof here.
Lemma 2.13. Let
![]() $\epsilon _0 \in (0,1]$
be a real number. Let
$\epsilon _0 \in (0,1]$
be a real number. Let
![]() $(X\ni x, B)$
be an lc surface germ, Y a smooth surface and
$(X\ni x, B)$
be an lc surface germ, Y a smooth surface and
![]() $f:Y\to X\ni x$
a projective birational morphism with the dual graph
$f:Y\to X\ni x$
a projective birational morphism with the dual graph
![]() ${\mathcal {DG}}$
. Let
${\mathcal {DG}}$
. Let
![]() $\{E_k\}_{1\leq k\leq m}$
be the set of vertices of
$\{E_k\}_{1\leq k\leq m}$
be the set of vertices of
![]() $\mathcal {DG}$
, and
$\mathcal {DG}$
, and
![]() $w_k:=-E_k\cdot E_k$
,
$w_k:=-E_k\cdot E_k$
,
![]() $a_k:=a(E_k,X,B)$
for each k. Suppose that
$a_k:=a(E_k,X,B)$
for each k. Suppose that
![]() $a_k\leq 1$
for any
$a_k\leq 1$
for any
![]() $1\leq k\leq m$
, then we have the following:
$1\leq k\leq m$
, then we have the following:
-
(1)
 $w_k\leq \frac {2}{a_k}$
if
$w_k\leq \frac {2}{a_k}$
if
 $a_k>0$
, and in particular,
$a_k>0$
, and in particular,
 $w_k\leq \frac {2}{\epsilon _0}$
for
$w_k\leq \frac {2}{\epsilon _0}$
for
 $1\leq k\leq m$
if
$1\leq k\leq m$
if
 $\mathrm {mld}(X\ni x, B)\geq \epsilon _0$
.
$\mathrm {mld}(X\ni x, B)\geq \epsilon _0$
. -
(2) If
 $w_k\geq 2$
for some k, then for any
$w_k\geq 2$
for some k, then for any
 $E_{k_1},E_{k_2}$
which are adjacent to
$E_{k_1},E_{k_2}$
which are adjacent to
 $E_k$
, we have
$E_k$
, we have
 $2a_k\leq a_{k_1}+a_{k_2}$
. Moreover, if the equality holds, then
$2a_k\leq a_{k_1}+a_{k_2}$
. Moreover, if the equality holds, then
 $f_*^{-1}B\cdot E_k=0$
, and either
$f_*^{-1}B\cdot E_k=0$
, and either
 $w_k=2$
or
$w_k=2$
or
 $a_k=a_{k_1}=a_{k_2}=0$
.
$a_k=a_{k_1}=a_{k_2}=0$
. -
(3) If
 $E_{k_0}$
is a fork, then for any
$E_{k_0}$
is a fork, then for any
 $E_{k_1}, E_{k_2}, E_{k_3}$
which are adjacent to
$E_{k_1}, E_{k_2}, E_{k_3}$
which are adjacent to
 $E_{k_0}$
with
$E_{k_0}$
with
 $w_{k_i}\geq 2$
for
$w_{k_i}\geq 2$
for
 $0\leq i\leq 2$
,
$0\leq i\leq 2$
,
 $a_{k_3}\geq a_{k_0}$
. Moreover, if the equality holds, then
$a_{k_3}\geq a_{k_0}$
. Moreover, if the equality holds, then
 $w_{k_i}=2$
and
$w_{k_i}=2$
and
 $f_*^{-1}B\cdot E_{k_i}=0$
for
$f_*^{-1}B\cdot E_{k_i}=0$
for
 $0\leq i\leq 2$
.
$0\leq i\leq 2$
. -
(4) Let
 $E_{k_0},E_{k_1},E_{k_2}$
be three vertices, such that
$E_{k_0},E_{k_1},E_{k_2}$
be three vertices, such that
 $E_{k_1},E_{k_2}$
are adjacent to
$E_{k_1},E_{k_2}$
are adjacent to
 $E_{k_0}$
. Assume that
$E_{k_0}$
. Assume that
 $a_{k_1}\geq a_{k_2}$
,
$a_{k_1}\geq a_{k_2}$
,
 $a_{k_1}\geq \epsilon _0$
, and
$a_{k_1}\geq \epsilon _0$
, and
 $w_{k_0}\geq 3$
, then
$w_{k_0}\geq 3$
, then
 $a_{k_1}-a_{k_0}\geq \frac {\epsilon _0}{3}$
.
$a_{k_1}-a_{k_0}\geq \frac {\epsilon _0}{3}$
. -
(5) If
 $E_{k_0}$
is a fork, and there exist three vertices
$E_{k_0}$
is a fork, and there exist three vertices
 $E_{k_1}, E_{k_2}, E_{k_3}$
which are adjacent to
$E_{k_1}, E_{k_2}, E_{k_3}$
which are adjacent to
 $E_{k_0}$
with
$E_{k_0}$
with
 $w_{k_i}\geq 2$
for
$w_{k_i}\geq 2$
for
 $0\leq i\leq 3$
, then
$0\leq i\leq 3$
, then
 $a(E,X,B)\geq a_{k_0}$
for any vertex E of
$a(E,X,B)\geq a_{k_0}$
for any vertex E of
 ${\mathcal {DG}}$
.
${\mathcal {DG}}$
. -
(6) Let
 $\{E_{k_i}\}_{0\leq i\leq m'}$
be a set of distinct vertices, such that
$\{E_{k_i}\}_{0\leq i\leq m'}$
be a set of distinct vertices, such that
 $E_{k_i}$
is adjacent to
$E_{k_i}$
is adjacent to
 $E_{k_{i+1}}$
for
$E_{k_{i+1}}$
for
 $0\leq i\leq m'-1$
, where
$0\leq i\leq m'-1$
, where
 $m'\geq 2$
. If
$m'\geq 2$
. If
 $a_{k_0}=a_{k_{m'}}=\mathrm {mld}(X\ni x, B)>0$
and
$a_{k_0}=a_{k_{m'}}=\mathrm {mld}(X\ni x, B)>0$
and
 $w_{k_i}\geq 2$
for
$w_{k_i}\geq 2$
for
 $1\leq i\leq m'-1$
, then
$1\leq i\leq m'-1$
, then
 $a_{k_0}=a_{k_1}=\cdots =a_{k_{m'}}$
and
$a_{k_0}=a_{k_1}=\cdots =a_{k_{m'}}$
and
 $w_{k_i}=2$
for
$w_{k_i}=2$
for
 $1\leq i\leq m'-1$
.
$1\leq i\leq m'-1$
.
Proof. For (1), we may write
![]() $K_Y+f_*^{-1}B+\sum _{1\leq i\leq m}(1-a_i)E_i=f^*(K_X+B).$
For each
$K_Y+f_*^{-1}B+\sum _{1\leq i\leq m}(1-a_i)E_i=f^*(K_X+B).$
For each
![]() $1\leq k\leq m$
, we have
$1\leq k\leq m$
, we have
![]() $0=(K_Y+f_*^{-1}B+\sum _{1\leq i\leq m}(1-a_i)E_i)\cdot E_k,$
or equivalently,
$0=(K_Y+f_*^{-1}B+\sum _{1\leq i\leq m}(1-a_i)E_i)\cdot E_k,$
or equivalently,
So
![]() $a_kw_k\le 2$
, and
$a_kw_k\le 2$
, and
![]() $w_k\le \frac {2}{a_k}$
.
$w_k\le \frac {2}{a_k}$
.
For (2), by (2.1),
![]() $2a_k\leq a_kw_k\le a_{k_1}+a_{k_2}-f_*^{-1}B\cdot E_k\leq a_{k_1}+a_{k_2}.$
If
$2a_k\leq a_kw_k\le a_{k_1}+a_{k_2}-f_*^{-1}B\cdot E_k\leq a_{k_1}+a_{k_2}.$
If
![]() $2a_k=a_{k_1}+a_{k_2}$
, then
$2a_k=a_{k_1}+a_{k_2}$
, then
![]() $f_*^{-1}B\cdot E_k=0$
, and either
$f_*^{-1}B\cdot E_k=0$
, and either
![]() $w_k=2$
or
$w_k=2$
or
![]() $a_k=a_{k_1}=a_{k_2}=0$
.
$a_k=a_{k_1}=a_{k_2}=0$
.
For (3), let
![]() $k=k_i$
in (2.1) for
$k=k_i$
in (2.1) for
![]() $i=1,2$
,
$i=1,2$
,
 $$ \begin{align*}a_{k_i}w_{k_i}\leq 1+a_{k_0}-\left(\sum_{j\neq k_0,k_i}(1-a_j)E_j\cdot E_{k_i}+f_*^{-1}B\cdot E_{k_i}\right)\leq 1+a_{k_0},\end{align*} $$
$$ \begin{align*}a_{k_i}w_{k_i}\leq 1+a_{k_0}-\left(\sum_{j\neq k_0,k_i}(1-a_j)E_j\cdot E_{k_i}+f_*^{-1}B\cdot E_{k_i}\right)\leq 1+a_{k_0},\end{align*} $$
or
![]() $a_{k_i}\le \frac {1+a_{k_0}}{w_{k_i}}$
. Thus, let
$a_{k_i}\le \frac {1+a_{k_0}}{w_{k_i}}$
. Thus, let
![]() $k=k_0$
in (2.1), we have:
$k=k_0$
in (2.1), we have:
 $$ \begin{align*} a_{k_3}\ge a_{k_0}w_{k_0}+1-a_{k_1}-a_{k_2}+f_*^{-1}B\cdot E_{k_0} &\ge a_{k_0}\left(w_{k_0}-\frac{1}{w_{k_1}}-\frac{1}{w_{k_2}}\right)+\left(1-\frac{1}{w_{k_1}}-\frac{1}{w_{k_2}}\right) \\ &\geq a_{k_0}. \end{align*} $$
$$ \begin{align*} a_{k_3}\ge a_{k_0}w_{k_0}+1-a_{k_1}-a_{k_2}+f_*^{-1}B\cdot E_{k_0} &\ge a_{k_0}\left(w_{k_0}-\frac{1}{w_{k_1}}-\frac{1}{w_{k_2}}\right)+\left(1-\frac{1}{w_{k_1}}-\frac{1}{w_{k_2}}\right) \\ &\geq a_{k_0}. \end{align*} $$
If the equality holds, then
![]() $w_{k_i}=2$
and
$w_{k_i}=2$
and
![]() $f_*^{-1}B\cdot E_i=0$
for
$f_*^{-1}B\cdot E_i=0$
for
![]() $0\leq i\leq 2$
.
$0\leq i\leq 2$
.
For (4), by (2.1), we have
![]() $a_{k_0}w_{k_0}\leq a_{k_1}+a_{k_2}-d$
, where
$a_{k_0}w_{k_0}\leq a_{k_1}+a_{k_2}-d$
, where
![]() $d:=f^{-1}_{*}B\cdot E_{k_0}+\sum _{j\neq k_1,k_2,{k_0}}(1-a_j)E_j\cdot E_{k_0}$
. Hence:
$d:=f^{-1}_{*}B\cdot E_{k_0}+\sum _{j\neq k_1,k_2,{k_0}}(1-a_j)E_j\cdot E_{k_0}$
. Hence:
 $$ \begin{align*} a_{k_1}-a_{k_0}\ge \frac{(w_{k_0}-1) a_{k_1}-a_{k_2}+d}{w_{k_0}}\geq \frac{(w_{k_0}-2)a_{k_1}}{w_{k_0}}\geq \frac{\epsilon_0}{3}. \end{align*} $$
$$ \begin{align*} a_{k_1}-a_{k_0}\ge \frac{(w_{k_0}-1) a_{k_1}-a_{k_2}+d}{w_{k_0}}\geq \frac{(w_{k_0}-2)a_{k_1}}{w_{k_0}}\geq \frac{\epsilon_0}{3}. \end{align*} $$
For (5), we may assume that
![]() $E\neq E_{k_0}$
. There exist
$E\neq E_{k_0}$
. There exist
![]() $m'+1$
distinct vertices
$m'+1$
distinct vertices
![]() $\{F_i\}_{0\leq i\leq m'}$
of
$\{F_i\}_{0\leq i\leq m'}$
of
![]() ${\mathcal {DG}}$
, such that:
${\mathcal {DG}}$
, such that:
-
•
 $F_0=E_{k_0}$
,
$F_0=E_{k_0}$
,
 $F_{m'}=E$
and
$F_{m'}=E$
and -
•
 $F_i$
is adjacent to
$F_i$
is adjacent to
 $F_{i+1}$
for
$F_{i+1}$
for
 $0\leq i\leq m'-1$
.
$0\leq i\leq m'-1$
.
Denote
![]() $a_i':=a(F_i,X,B)$
for
$a_i':=a(F_i,X,B)$
for
![]() $0\leq i\leq m'$
. By (3), we have
$0\leq i\leq m'$
. By (3), we have
![]() $a_1'\geq a_0'$
, and by (2),
$a_1'\geq a_0'$
, and by (2),
![]() $a_{i+1}'-a_{i}'\geq a_{i}'-a_{i-1}'$
for
$a_{i+1}'-a_{i}'\geq a_{i}'-a_{i-1}'$
for
![]() $1\leq i\leq m'-1$
. Thus,
$1\leq i\leq m'-1$
. Thus,
![]() $a_m'-a_0'\geq 0$
.
$a_m'-a_0'\geq 0$
.
For (6), by (2)
![]() $a_{k_0}\leq a_{k_1}\leq \ldots \leq a_{k_{m'-1}}\leq a_{k_{m'}}$
. Thus,
$a_{k_0}\leq a_{k_1}\leq \ldots \leq a_{k_{m'-1}}\leq a_{k_{m'}}$
. Thus,
![]() $a_{k_0}=\ldots =a_{k_{m'}}$
. By (2) again,
$a_{k_0}=\ldots =a_{k_{m'}}$
. By (2) again,
![]() $w_{k_i}=2$
for
$w_{k_i}=2$
for
![]() $1\leq i\leq m'-1$
.
$1\leq i\leq m'-1$
.
Lemma 2.14. Let
![]() $(X\ni x, B)$
be an lc surface germ. Let Y be a smooth surface and
$(X\ni x, B)$
be an lc surface germ. Let Y be a smooth surface and
![]() $f:Y\to X\ni x$
a birational morphism with the dual graph
$f:Y\to X\ni x$
a birational morphism with the dual graph
![]() ${\mathcal {DG}}$
. If
${\mathcal {DG}}$
. If
![]() ${\mathcal {DG}}$
contains a
${\mathcal {DG}}$
contains a
![]() $(-1)$
-curve
$(-1)$
-curve
![]() $E_0$
, then:
$E_0$
, then:
-
(1)
 $E_0$
can not be adjacent to two
$E_0$
can not be adjacent to two
 $(-2)$
-curves in
$(-2)$
-curves in
 ${\mathcal {DG}}$
,
${\mathcal {DG}}$
, -
(2) if either
 $\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
or
$\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
or
 $\mathrm {mld}(X\ni x, B)>0$
, then
$\mathrm {mld}(X\ni x, B)>0$
, then
 $E_0$
is not a fork in
$E_0$
is not a fork in
 ${\mathcal {DG}}$
and
${\mathcal {DG}}$
and -
(3) if
 $E,E_0,\ldots ,E_m$
are distinct vertices of
$E,E_0,\ldots ,E_m$
are distinct vertices of
 ${\mathcal {DG}}$
, such that E is adjacent to
${\mathcal {DG}}$
, such that E is adjacent to
 $E_0$
,
$E_0$
,
 $E_i$
is adjacent to
$E_i$
is adjacent to
 $E_{i+1}$
for
$E_{i+1}$
for
 $0\leq i\leq m-1$
, and
$0\leq i\leq m-1$
, and
 $-E_i\cdot E_i=2$
for
$-E_i\cdot E_i=2$
for
 $1\leq i\leq m$
, then
$1\leq i\leq m$
, then
 $m+1<-E\cdot E=w$
.
$m+1<-E\cdot E=w$
.
Proof. For (1), if
![]() $E_0$
is adjacent to two
$E_0$
is adjacent to two
![]() $(-2)$
-curves
$(-2)$
-curves
![]() $E_{k_1}$
and
$E_{k_1}$
and
![]() $E_{k_2}$
in
$E_{k_2}$
in
![]() ${\mathcal {DG}}$
, then we may contract
${\mathcal {DG}}$
, then we may contract
![]() $E_0$
and get a smooth model
$E_0$
and get a smooth model
![]() $f':Y'\to X\ni x$
over X, whose dual graph contains two adjacent
$f':Y'\to X\ni x$
over X, whose dual graph contains two adjacent
![]() $(-1)$
-curves, this contradicts the negativity lemma.
$(-1)$
-curves, this contradicts the negativity lemma.
By [Reference Kollár and Mori15, Theorem 4.7] and the assumptions in (2), the dual graph of the minimal resolution of
![]() $X\ni x$
is a tree. If
$X\ni x$
is a tree. If
![]() $E_0$
is a fork, we may contract
$E_0$
is a fork, we may contract
![]() $E_0$
and get a smooth model
$E_0$
and get a smooth model
![]() $f': Y'\to X\ni x$
, whose dual graph contains a cycle, this contradicts Lemma 2.12.
$f': Y'\to X\ni x$
, whose dual graph contains a cycle, this contradicts Lemma 2.12.
For (3), we will construct a sequence of contractions of
![]() $(-1)$
-curve
$(-1)$
-curve
![]() $X_0:=X\to X_1\to \ldots X_m\to X_{m+1}$
inductively. Let
$X_0:=X\to X_1\to \ldots X_m\to X_{m+1}$
inductively. Let
![]() $E_{X_k}$
be the strict transform of E on
$E_{X_k}$
be the strict transform of E on
![]() $X_k$
, and
$X_k$
, and
![]() $w_{X_k}:=-E_{X_k}\cdot E_{X_k}$
. For simplicity, we will always denote the strict transform of
$w_{X_k}:=-E_{X_k}\cdot E_{X_k}$
. For simplicity, we will always denote the strict transform of
![]() $E_k$
on
$E_k$
on
![]() $X_j$
by
$X_j$
by
![]() $E_k$
for all
$E_k$
for all
![]() $k,j$
. Let
$k,j$
. Let
![]() $f_1: X_0\to X_1$
be the contraction of
$f_1: X_0\to X_1$
be the contraction of
![]() $E_0$
on
$E_0$
on
![]() $X_0$
, then
$X_0$
, then
![]() $w_{X_1}=w-1$
, and
$w_{X_1}=w-1$
, and
![]() $E_1\cdot E_1=-1$
on
$E_1\cdot E_1=-1$
on
![]() $X_1$
. Let
$X_1$
. Let
![]() $f_2: X_1\to X_2$
be the contraction of
$f_2: X_1\to X_2$
be the contraction of
![]() $E_1$
on
$E_1$
on
![]() $X_1$
, then
$X_1$
, then
![]() $w_{X_2}=w_{X_1}-1=w-2$
, and
$w_{X_2}=w_{X_1}-1=w-2$
, and
![]() $E_2\cdot E_2=-1$
on
$E_2\cdot E_2=-1$
on
![]() $X_2$
. Repeating this procedure, we have
$X_2$
. Repeating this procedure, we have
![]() $f_k: X_{k-1}\to X_k$
the contraction of
$f_k: X_{k-1}\to X_k$
the contraction of
![]() $E_{k-1}$
, and
$E_{k-1}$
, and
![]() $w_{X_k}=w-k$
,
$w_{X_k}=w-k$
,
![]() $E_k\cdot E_k=-1$
on
$E_k\cdot E_k=-1$
on
![]() $X_k$
for
$X_k$
for
![]() $1\leq k\leq m+1$
. By the negativity lemma,
$1\leq k\leq m+1$
. By the negativity lemma,
![]() $w_{X_{m+1}}=w-(m+1)>0$
, and we are done.
$w_{X_{m+1}}=w-(m+1)>0$
, and we are done.
Lemma 2.15. Let
![]() $\gamma \in (0,1]$
be a real number. Let
$\gamma \in (0,1]$
be a real number. Let
![]() $(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
$(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
![]() $B_i$
are distinct prime divisors. Let Y be a smooth surface and
$B_i$
are distinct prime divisors. Let Y be a smooth surface and
![]() $f: Y\to X\ni x$
a birational morphism with the dual graph
$f: Y\to X\ni x$
a birational morphism with the dual graph
![]() ${\mathcal {DG}}$
. Let
${\mathcal {DG}}$
. Let
![]() $\{E_k\}_{0\leq k\leq m}$
be a vertex-induced subchain of
$\{E_k\}_{0\leq k\leq m}$
be a vertex-induced subchain of
![]() ${\mathcal {DG}}$
, such that
${\mathcal {DG}}$
, such that
![]() $E_k$
is adjacent to
$E_k$
is adjacent to
![]() $E_{k+1}$
for
$E_{k+1}$
for
![]() $0\leq k\leq m-1$
, and let
$0\leq k\leq m-1$
, and let
![]() $w_k:=-E_k\cdot E_k$
,
$w_k:=-E_k\cdot E_k$
,
![]() $a_k:=a(E_k,X,B)$
for all k. Suppose that
$a_k:=a(E_k,X,B)$
for all k. Suppose that
![]() $w_0=1$
,
$w_0=1$
,
![]() $E_0$
is adjacent to only one vertex
$E_0$
is adjacent to only one vertex
![]() $E_1$
of
$E_1$
of
![]() ${\mathcal {DG}}$
,
${\mathcal {DG}}$
,
![]() $a_k\leq 1$
, and
$a_k\leq 1$
, and
![]() $w_k\geq 2$
for each
$w_k\geq 2$
for each
![]() $k\geq 1$
, then:
$k\geq 1$
, then:
-
(1) if
 $\{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
, and
$\{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
, and
 $a_0<a_1$
, then
$a_0<a_1$
, then
 $m\leq \frac {1}{\gamma }$
,
$m\leq \frac {1}{\gamma }$
, -
(2) if
 $\sum _i n_ib_i-1\neq 0$
for all
$\sum _i n_ib_i-1\neq 0$
for all
 $n_i\in \mathbb {Z}_{\geq 0}$
, and
$n_i\in \mathbb {Z}_{\geq 0}$
, and
 $a_0\leq a_1$
, then
$a_0\leq a_1$
, then
 $a_0<a_1$
and
$a_0<a_1$
and -
(3) if
 $\{\sum _i n_ib_i-1\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
, and
$\{\sum _i n_ib_i-1\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
, and
 $a_0\leq a_1$
, then
$a_0\leq a_1$
, then
 $m\leq \frac {1}{\gamma }$
.
$m\leq \frac {1}{\gamma }$
.
Proof. We may write
![]() $K_Y+f_*^{-1}B+\sum _i (1-a_i)E_i=f^*(K_X+B)$
, then:
$K_Y+f_*^{-1}B+\sum _i (1-a_i)E_i=f^*(K_X+B)$
, then:
Since
![]() $E_0$
is adjacent to only one vertex
$E_0$
is adjacent to only one vertex
![]() $E_1$
of
$E_1$
of
![]() ${\mathcal {DG}}$
, by (2.2), we have:
${\mathcal {DG}}$
, by (2.2), we have:
For (1), since
![]() $1\ge a_1>a_0$
, it follows that
$1\ge a_1>a_0$
, it follows that
![]() $f_*^{-1}B\cdot E_0-1\in \{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Thus,
$f_*^{-1}B\cdot E_0-1\in \{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Thus,
![]() $a_1-a_0\geq \gamma $
. By Lemma 2.13(2), we have
$a_1-a_0\geq \gamma $
. By Lemma 2.13(2), we have
![]() $a_{i+1}-a_i\geq a_1-a_0\geq \gamma $
for any
$a_{i+1}-a_i\geq a_1-a_0\geq \gamma $
for any
![]() $0\leq i\leq m-1$
, and
$0\leq i\leq m-1$
, and
![]() $1\geq a_m\ge \gamma m$
. So
$1\geq a_m\ge \gamma m$
. So
![]() $m\leq \frac {1}{\gamma }$
.
$m\leq \frac {1}{\gamma }$
.
For (2), since
![]() $f_*^{-1}B\cdot E_0-1=\sum _i n_ib_i-1\neq 0$
for some
$f_*^{-1}B\cdot E_0-1=\sum _i n_ib_i-1\neq 0$
for some
![]() $n_i\in \mathbb {Z}_{\geq 0}$
,
$n_i\in \mathbb {Z}_{\geq 0}$
,
![]() $a_0<a_1$
,
$a_0<a_1$
,
(3) follows immediately from (1) and (2).
2.4 Sequence of blow-ups
Definition 2.16. Let
![]() $X\ni x$
be a smooth surface germ. We say
$X\ni x$
be a smooth surface germ. We say
![]() $X_n\to X_{n-1}\to \cdots \to X_1\to X_0:=X$
is a sequence of blow-ups with the data
$X_n\to X_{n-1}\to \cdots \to X_1\to X_0:=X$
is a sequence of blow-ups with the data
![]() $(f_i,F_i,x_i\in X_i)$
if:
$(f_i,F_i,x_i\in X_i)$
if:
-
•
 $f_i: X_i\to X_{i-1}$
is the blow-up of
$f_i: X_i\to X_{i-1}$
is the blow-up of
 $X_{i-1}$
at a closed point
$X_{i-1}$
at a closed point
 $x_{i-1}\in X_{i-1}$
, with the exceptional divisor
$x_{i-1}\in X_{i-1}$
, with the exceptional divisor
 $F_i$
for any
$F_i$
for any
 $1\leq i\leq n$
, where
$1\leq i\leq n$
, where
 $x_0:=x$
and
$x_0:=x$
and -
•
 $x_i\in F_i$
for any
$x_i\in F_i$
for any
 $1\leq i\leq n-1$
.
$1\leq i\leq n-1$
.
In particular,
![]() $F_n$
is the only exceptional
$F_n$
is the only exceptional
![]() $(-1)$
-curve over X.
$(-1)$
-curve over X.
For convenience, we will always denote the strict transform of
![]() $F_i$
on
$F_i$
on
![]() $X_j$
by
$X_j$
by
![]() $F_i$
for any
$F_i$
for any
![]() $n\ge j\ge i$
.
$n\ge j\ge i$
.
The following lemma is well known. For a proof, see for example, [Reference Han and Luo9, Lemma 3.15].
Lemma 2.17. Let
![]() $(X\ni x,B)$
be an lc surface germ, such that
$(X\ni x,B)$
be an lc surface germ, such that
![]() $\mathrm {mld}(X\ni x, B)>1$
, then
$\mathrm {mld}(X\ni x, B)>1$
, then
![]() $\mathrm {mld}(X\ni x, B)=2-\operatorname {mult}_x B$
, and there is exactly one prime divisor E over
$\mathrm {mld}(X\ni x, B)=2-\operatorname {mult}_x B$
, and there is exactly one prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x,B)$
.
$a(E,X,B)=\mathrm {mld}(X\ni x,B)$
.
Lemma 2.18 ([Reference Mustaţǎ and Nakamura17, Lemma 4.2])
Let
![]() $X\ni x$
be a smooth surface germ, and
$X\ni x$
be a smooth surface germ, and
![]() $X_{l_0}\to \cdots \to X_1\to X_0:=X$
a sequence of blow-ups with the data
$X_{l_0}\to \cdots \to X_1\to X_0:=X$
a sequence of blow-ups with the data
![]() $(f_i,E_i,x_i\in X_i)$
, then
$(f_i,E_i,x_i\in X_i)$
, then
![]() $a(E_{l_0},X,0)\leq 2^{l_0}$
.
$a(E_{l_0},X,0)\leq 2^{l_0}$
.
2.5 Extracting divisors computing MLDs
Lemma 2.19. Let
![]() $(X\ni x,B)$
be an lc surface germ. Let
$(X\ni x,B)$
be an lc surface germ. Let
![]() $h: W\to (X,B)$
be a log resolution, and
$h: W\to (X,B)$
be a log resolution, and
![]() $S=\{E_j\}$
a finite set of valuations of h-exceptional prime divisors over
$S=\{E_j\}$
a finite set of valuations of h-exceptional prime divisors over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E_j,X,B)\leq 1$
for all j. Then there exist a smooth surface Y and a projective birational morphism
$a(E_j,X,B)\leq 1$
for all j. Then there exist a smooth surface Y and a projective birational morphism
![]() $f: Y\to X\ni x$
with the following properties.
$f: Y\to X\ni x$
with the following properties.
-
(1)
 $K_Y+B_Y=f^*(K_X+B)$
for some
$K_Y+B_Y=f^*(K_X+B)$
for some
 $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
 $B_Y\ge 0$
on Y,
$B_Y\ge 0$
on Y, -
(2) each valuation in S corresponds to some f-exceptional divisor on Y and
-
(3) each f-exceptional
 $(-1)$
-curve corresponds to some valuation in S.
$(-1)$
-curve corresponds to some valuation in S.
Proof.
where
![]() $B_{W}\ge 0$
and
$B_{W}\ge 0$
and
![]() $F_W\ge 0$
are
$F_W\ge 0$
are
![]() $\mathbb {R}$
-divisors with no common components. We construct a sequence of
$\mathbb {R}$
-divisors with no common components. We construct a sequence of
![]() $(K_{W}+B_{W})$
-MMP over X as follows. Each time we will contract a
$(K_{W}+B_{W})$
-MMP over X as follows. Each time we will contract a
![]() $(-1)$
-curve whose support is contained in
$(-1)$
-curve whose support is contained in
![]() $F_W$
. Suppose that
$F_W$
. Suppose that
![]() $K_{W}+B_{W}$
is not nef over X, then
$K_{W}+B_{W}$
is not nef over X, then
![]() $F_W\neq 0$
. By the negativity lemma, there exists a h-exceptional irreducible curve
$F_W\neq 0$
. By the negativity lemma, there exists a h-exceptional irreducible curve
![]() $C\subseteq \operatorname {Supp} F_W$
, such that
$C\subseteq \operatorname {Supp} F_W$
, such that
![]() $F_W\cdot C=(K_{W}+B_{W})\cdot C<0$
. Since
$F_W\cdot C=(K_{W}+B_{W})\cdot C<0$
. Since
![]() $B_{W}\cdot C\ge 0$
,
$B_{W}\cdot C\ge 0$
,
![]() $K_{W}\cdot C<0$
. Thus, C is a h-exceptional
$K_{W}\cdot C<0$
. Thus, C is a h-exceptional
![]() $(-1)$
-curve. We may contract C and get a smooth surface
$(-1)$
-curve. We may contract C and get a smooth surface
![]() $Y_0:=W\to Y_1$
over X. We may continue this process, and finally reach a smooth model
$Y_0:=W\to Y_1$
over X. We may continue this process, and finally reach a smooth model
![]() $Y_k$
on which
$Y_k$
on which
![]() $K_{Y_k}+B_{Y_k}$
is nef over X, where
$K_{Y_k}+B_{Y_k}$
is nef over X, where
![]() $B_{Y_k}$
is the strict transform of
$B_{Y_k}$
is the strict transform of
![]() $B_{W}$
on
$B_{W}$
on
![]() $Y_k$
. By the negativity lemma,
$Y_k$
. By the negativity lemma,
![]() $F_W$
is contracted in the MMP, thus
$F_W$
is contracted in the MMP, thus
![]() $K_{Y_k}+B_{Y_k}=h_k^{*}(K_X+B)$
, where
$K_{Y_k}+B_{Y_k}=h_k^{*}(K_X+B)$
, where
![]() $h_k:Y_k\to X$
, since
$h_k:Y_k\to X$
, since
![]() $a(E_j,X,B)\le 1$
,
$a(E_j,X,B)\le 1$
,
![]() $E_j$
is not contracted in the MMP for any
$E_j$
is not contracted in the MMP for any
![]() $E_j\in S$
.
$E_j\in S$
.
We now construct a sequence of smooth models over X,
![]() $Y_k\to Y_{k+1}\to \cdots $
, by contracting a curve
$Y_k\to Y_{k+1}\to \cdots $
, by contracting a curve
![]() $C'$
satisfying the following conditions in each step.
$C'$
satisfying the following conditions in each step.
-
•
 $C'$
is an exceptional
$C'$
is an exceptional
 $(-1)$
-curve over X and
$(-1)$
-curve over X and -
•
 $C'\notin S$
.
$C'\notin S$
.
Since each time the Picard number of the variety will drop by one, after finitely many steps, we will reach a smooth model Y over X, such that
![]() $f:Y\to X$
and
$f:Y\to X$
and
![]() $(Y,B_Y)$
satisfy (1)–(3), where
$(Y,B_Y)$
satisfy (1)–(3), where
![]() $B_Y$
is the strict transform of
$B_Y$
is the strict transform of
![]() $B_{Y_k}$
on Y.
$B_{Y_k}$
on Y.
We will need Lemma 2.20 to prove our main results. It may be well known to experts. Lemma 2.20(1)–(4) could be proved by constructing a sequence of blow-ups (c.f. [Reference Chen and Han5, Lemma 4.3]). We give another proof here.
We remark that Lemma 2.20(5) will only be applied to prove Theorem 1.2.
Lemma 2.20. Let
![]() $(X\ni x,B)$
be an lc surface germ, such that
$(X\ni x,B)$
be an lc surface germ, such that
![]() $1\geq \mathrm {mld}(X\ni x,B)\neq \operatorname {pld}(X\ni x,B)$
. There exist a smooth surface Y and a projective birational morphism
$1\geq \mathrm {mld}(X\ni x,B)\neq \operatorname {pld}(X\ni x,B)$
. There exist a smooth surface Y and a projective birational morphism
![]() $f: Y\to X$
with the dual graph
$f: Y\to X$
with the dual graph
![]() ${\mathcal {DG}}$
, such that:
${\mathcal {DG}}$
, such that:
-
(1)
 $K_Y+B_Y=f^*(K_X+B)$
for some
$K_Y+B_Y=f^*(K_X+B)$
for some
 $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
 $B_Y\ge 0$
on Y,
$B_Y\ge 0$
on Y, -
(2) there is only one f-exceptional divisor
 $E_0$
, such that
$E_0$
, such that
 $a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
,
$a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
, -
(3)
 $E_0$
is the only
$E_0$
is the only
 $(-1)$
-curve of
$(-1)$
-curve of
 ${\mathcal {DG}}$
and
${\mathcal {DG}}$
and -
(4)
 ${\mathcal {DG}}$
is a chain.
${\mathcal {DG}}$
is a chain.
Moreover, if
![]() $X\ni x$
is not smooth, let
$X\ni x$
is not smooth, let
![]() $\widetilde {f}: \widetilde {X}\to X\ni x$
be the minimal resolution of
$\widetilde {f}: \widetilde {X}\to X\ni x$
be the minimal resolution of
![]() $X\ni x$
, and let
$X\ni x$
, and let
![]() $g: Y\to \widetilde {X}$
be the morphism, such that
$g: Y\to \widetilde {X}$
be the morphism, such that
![]() $\widetilde {f}\circ g=f$
, then:
$\widetilde {f}\circ g=f$
, then:
-
(5) there exist a
 $\widetilde {f}$
-exceptional prime divisor
$\widetilde {f}$
-exceptional prime divisor
 $\widetilde {E}$
on
$\widetilde {E}$
on
 $\widetilde {X}$
and a closed point
$\widetilde {X}$
and a closed point
 $\widetilde {x}\in \widetilde {E}$
, such that
$\widetilde {x}\in \widetilde {E}$
, such that
 $a(\widetilde {E},X,B)=\operatorname {pld}(X\ni x, B)$
, and
$a(\widetilde {E},X,B)=\operatorname {pld}(X\ni x, B)$
, and
 $\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for all g-exceptional divisors E.
$\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for all g-exceptional divisors E.
Proof. By Lemma 2.19, we can find a smooth surface
![]() $Y_0$
and a birational morphism
$Y_0$
and a birational morphism
![]() $h:Y_0\to X\ni x$
, such that
$h:Y_0\to X\ni x$
, such that
![]() $a(E_0',X,B)=\mathrm {mld}(X\ni x, B)$
for some h-exceptional divisor
$a(E_0',X,B)=\mathrm {mld}(X\ni x, B)$
for some h-exceptional divisor
![]() $E_0'$
, and
$E_0'$
, and
![]() $K_{Y_0}+B_{Y_0}=h^*(K_X+B)$
for some
$K_{Y_0}+B_{Y_0}=h^*(K_X+B)$
for some
![]() $B_{Y_0}\ge 0$
on
$B_{Y_0}\ge 0$
on
![]() $Y_0$
.
$Y_0$
.
We now construct a sequence of smooth models over X,
![]() $Y_0\to Y_{1}\to \cdots $
, by contracting a curve
$Y_0\to Y_{1}\to \cdots $
, by contracting a curve
![]() $C'$
satisfying the following conditions in each step.
$C'$
satisfying the following conditions in each step.
-
•
 $C'$
is an exceptional
$C'$
is an exceptional
 $(-1)$
-curve over X and
$(-1)$
-curve over X and -
• there exists
 $C''\neq C'$
over X, such that
$C''\neq C'$
over X, such that
 $a(C'',X,B)=\mathrm {mld}(X\ni x, B)$
.
$a(C'',X,B)=\mathrm {mld}(X\ni x, B)$
.
Since each time the Picard number of the variety will drop by one, after finitely many steps, we will reach a smooth model Y over X, such that
![]() $f:Y\to X$
and
$f:Y\to X$
and
![]() $(Y,B_Y)$
satisfy (1), where
$(Y,B_Y)$
satisfy (1), where
![]() $B_Y$
is the strict transform of
$B_Y$
is the strict transform of
![]() $B_{Y_0}$
on Y. Since
$B_{Y_0}$
on Y. Since
![]() $\mathrm {mld}(X\ni x,B)\neq \operatorname {pld}(X\ni x,B)$
, by the construction of Y, there exists a curve
$\mathrm {mld}(X\ni x,B)\neq \operatorname {pld}(X\ni x,B)$
, by the construction of Y, there exists a curve
![]() $E_0$
on Y satisfying (2)–(3).
$E_0$
on Y satisfying (2)–(3).
For (4), by [Reference Kollár and Mori15, Theorem 4.7], the dual graph of the minimal resolution
![]() $\widetilde {f}:\widetilde {X}\to X\ni x$
is a tree whose vertices are smooth rational curves. Since Y is smooth, f factors through
$\widetilde {f}:\widetilde {X}\to X\ni x$
is a tree whose vertices are smooth rational curves. Since Y is smooth, f factors through
![]() $\widetilde {f}$
. By Lemma 2.12, the dual graph
$\widetilde {f}$
. By Lemma 2.12, the dual graph
![]() ${\mathcal {DG}}$
of f is a tree whose vertices are smooth rational curves. It suffices to show that there is no fork in
${\mathcal {DG}}$
of f is a tree whose vertices are smooth rational curves. It suffices to show that there is no fork in
![]() ${\mathcal {DG}}$
. By Lemma 2.14(2),
${\mathcal {DG}}$
. By Lemma 2.14(2),
![]() $E_0$
is not a fork. Suppose that
$E_0$
is not a fork. Suppose that
![]() ${\mathcal {DG}}$
contains a fork
${\mathcal {DG}}$
contains a fork
![]() $E'\neq E_0$
, by (3) and (5) of Lemma 2.13, we have
$E'\neq E_0$
, by (3) and (5) of Lemma 2.13, we have
![]() $a(E',X,B)\leq a(E_0,X,B)$
, this contradicts (2). Thus,
$a(E',X,B)\leq a(E_0,X,B)$
, this contradicts (2). Thus,
![]() ${\mathcal {DG}}$
is a chain.
${\mathcal {DG}}$
is a chain.
For (5), since there exists only one f-exceptional
![]() $(-1)$
-curve, there is at most one closed point
$(-1)$
-curve, there is at most one closed point
![]() $\widetilde {x}\in \widetilde {X}$
, such that
$\widetilde {x}\in \widetilde {X}$
, such that
![]() $\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for all g-exceptional divisors E. Thus, the dual graph of g, which is denoted by
$\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for all g-exceptional divisors E. Thus, the dual graph of g, which is denoted by
![]() ${\mathcal {DG}}'$
, is a vertex-induced connected subchain of
${\mathcal {DG}}'$
, is a vertex-induced connected subchain of
![]() ${\mathcal {DG}}$
by all g-exceptional divisors. Since
${\mathcal {DG}}$
by all g-exceptional divisors. Since
![]() $\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
, we have
$\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
, we have
![]() ${\mathcal {DG}}'\subsetneq {\mathcal {DG}}$
.
${\mathcal {DG}}'\subsetneq {\mathcal {DG}}$
.
We may index the vertices of
![]() ${\mathcal {DG}}$
as
${\mathcal {DG}}$
as
![]() $\{E_i\}_{-n_1\leq i\leq n_2}$
for
$\{E_i\}_{-n_1\leq i\leq n_2}$
for
![]() $n_1,n_2\in \mathbb {Z}_{\geq 0}$
, such that
$n_1,n_2\in \mathbb {Z}_{\geq 0}$
, such that
![]() $E_i$
is adjacent to
$E_i$
is adjacent to
![]() $E_{i+1}$
, and
$E_{i+1}$
, and
![]() $a_i:=a(E_i,X,B)$
for all possible i. We may assume that the set of vertices of
$a_i:=a(E_i,X,B)$
for all possible i. We may assume that the set of vertices of
![]() ${\mathcal {DG}} '$
is
${\mathcal {DG}} '$
is
![]() $\{E_j\}_{-n_1'\leq j\leq n_2'}$
, where
$\{E_j\}_{-n_1'\leq j\leq n_2'}$
, where
![]() $0\leq n_1'\leq n_1$
and
$0\leq n_1'\leq n_1$
and
![]() $0\leq n_2'\leq n_2$
(see Figure 1). If
$0\leq n_2'\leq n_2$
(see Figure 1). If
![]() $n_1>n_1'$
, then by Lemma 2.13(2),
$n_1>n_1'$
, then by Lemma 2.13(2),
![]() $a_{k}-a_{-n_1'-1}\geq \min \{0,a_{-1}-a_{0}\}\geq 0$
for all
$a_{k}-a_{-n_1'-1}\geq \min \{0,a_{-1}-a_{0}\}\geq 0$
for all
![]() $-n_1\leq k<-n_1' $
. If
$-n_1\leq k<-n_1' $
. If
![]() $n_2>n_2'$
, then again by Lemma 2.13(2),
$n_2>n_2'$
, then again by Lemma 2.13(2),
![]() $a_{k'}-a_{n_2'+1}\geq \min \{0,a_{1}-a_{0}\}\geq 0$
for all
$a_{k'}-a_{n_2'+1}\geq \min \{0,a_{1}-a_{0}\}\geq 0$
for all
![]() $n_2'< k'\leq n_2$
. Set
$n_2'< k'\leq n_2$
. Set
![]() $a_{-n_1-1}=1, E_{-n_1-1}=E_{-n_1}$
if
$a_{-n_1-1}=1, E_{-n_1-1}=E_{-n_1}$
if
![]() $n_1=n_1'$
, and set
$n_1=n_1'$
, and set
![]() $a_{n_2+1}=1,E_{n_2+1}=E_{n_2}$
if
$a_{n_2+1}=1,E_{n_2+1}=E_{n_2}$
if
![]() $n_2=n_2'$
. Then
$n_2=n_2'$
. Then
![]() $\min \{a_{n_2+1}, a_{-n_1-1}\}=\operatorname {pld}(X\ni x, B)$
, and
$\min \{a_{n_2+1}, a_{-n_1-1}\}=\operatorname {pld}(X\ni x, B)$
, and
![]() $\widetilde {x}= g(E_{-n_1'-1})\cap g(E_{n_2+1})\in \widetilde {E}$
, where
$\widetilde {x}= g(E_{-n_1'-1})\cap g(E_{n_2+1})\in \widetilde {E}$
, where
![]() $a(\widetilde {E},X,B)=\operatorname {pld}(X\ni x, B)$
.
$a(\widetilde {E},X,B)=\operatorname {pld}(X\ni x, B)$
.

Figure 1 The dual graph of f.
The following lemma gives an upper bound for number of vertices of a certain kind of
![]() ${\mathcal {DG}}$
constructed in Lemma 2.20, with the additional assumption that
${\mathcal {DG}}$
constructed in Lemma 2.20, with the additional assumption that
![]() $\mathrm {mld}(X\ni x, B)$
is bounded from below by a positive real number.
$\mathrm {mld}(X\ni x, B)$
is bounded from below by a positive real number.
Lemma 2.21. Let
![]() $\epsilon _0\in (0,1]$
be a real number. Then
$\epsilon _0\in (0,1]$
be a real number. Then
![]() $N_0':=\lfloor \frac {8}{\epsilon _0}\rfloor $
satisfies the following properties.
$N_0':=\lfloor \frac {8}{\epsilon _0}\rfloor $
satisfies the following properties.
Let
![]() $(X\ni x,B:=\sum b_iB_i)$
be an lc surface germ, such that
$(X\ni x,B:=\sum b_iB_i)$
be an lc surface germ, such that
![]() $\mathrm {mld}(X\ni x,B)\geq \epsilon _0$
, where
$\mathrm {mld}(X\ni x,B)\geq \epsilon _0$
, where
![]() $B_i$
are distinct prime divisors. Let Y be a smooth surface, and
$B_i$
are distinct prime divisors. Let Y be a smooth surface, and
![]() $f: Y\to X\ni x$
a birational morphism with the dual graph
$f: Y\to X\ni x$
a birational morphism with the dual graph
![]() ${\mathcal {DG}}$
, such that:
${\mathcal {DG}}$
, such that:
-
•
 $K_Y+B_Y=f^*(K_X+B)$
for some
$K_Y+B_Y=f^*(K_X+B)$
for some
 $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
 $B_Y\geq 0$
on Y,
$B_Y\geq 0$
on Y, -
•
 ${\mathcal {DG}}$
is a chain with only one
${\mathcal {DG}}$
is a chain with only one
 $(-1)$
-curve
$(-1)$
-curve
 $E_0$
,
$E_0$
, -
•
 $a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
and
$a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
and -
•
 $E_0$
is adjacent to two vertices of
$E_0$
is adjacent to two vertices of
 ${\mathcal {DG}}$
.
${\mathcal {DG}}$
.
Then the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $N_0'$
.
$N_0'$
.
Proof. Let
![]() $\{E_i\}_{-n_1\leq i\leq n_2}$
be the vertices of
$\{E_i\}_{-n_1\leq i\leq n_2}$
be the vertices of
![]() ${\mathcal {DG}}$
, such that
${\mathcal {DG}}$
, such that
![]() $E_i$
is adjacent to
$E_i$
is adjacent to
![]() $E_{i+1}$
for
$E_{i+1}$
for
![]() $-n_1\leq i\leq n_2-1$
, and
$-n_1\leq i\leq n_2-1$
, and
![]() $w_i:=-(E_i\cdot E_i), a_i:=a(E_i,X,B)$
for all i. We may assume that
$w_i:=-(E_i\cdot E_i), a_i:=a(E_i,X,B)$
for all i. We may assume that
![]() $E_0$
is adjacent to two vertices
$E_0$
is adjacent to two vertices
![]() $E_{-1}, E_1$
of
$E_{-1}, E_1$
of
![]() ${\mathcal {DG}}$
.
${\mathcal {DG}}$
.

By Lemma 2.14(1), we may assume that
![]() $w_{-1}>2$
. By (2) and (4) of Lemma 2.13,
$w_{-1}>2$
. By (2) and (4) of Lemma 2.13,
![]() $a_{i-1}-a_i\geq \frac {\epsilon _0}{3}$
for any
$a_{i-1}-a_i\geq \frac {\epsilon _0}{3}$
for any
![]() $-n_1+1\leq i\leq -1$
, and
$-n_1+1\leq i\leq -1$
, and
![]() $a_{-1}\geq \frac {\epsilon _0}{3}$
. Since
$a_{-1}\geq \frac {\epsilon _0}{3}$
. Since
![]() $a_{-n_1}\leq 1$
,
$a_{-n_1}\leq 1$
,
![]() $n_1\leq \frac {3}{\epsilon _0}$
. Similarly,
$n_1\leq \frac {3}{\epsilon _0}$
. Similarly,
![]() $n_2-n'\le \frac {3}{\epsilon _0}$
, where
$n_2-n'\le \frac {3}{\epsilon _0}$
, where
![]() $n'$
is the largest nonnegative integer, such that
$n'$
is the largest nonnegative integer, such that
![]() $w_i=2$
for any
$w_i=2$
for any
![]() $1\le i\le n'$
. By Lemma 2.13(1),
$1\le i\le n'$
. By Lemma 2.13(1),
![]() $w_{-1}\leq \frac {2}{\epsilon _0}$
, and by Lemma 2.14(3),
$w_{-1}\leq \frac {2}{\epsilon _0}$
, and by Lemma 2.14(3),
![]() $n'<\frac {2}{\epsilon _0}-1$
. Hence,
$n'<\frac {2}{\epsilon _0}-1$
. Hence,
![]() $n_1+n_2+1$
, the number of vertices of
$n_1+n_2+1$
, the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $\frac {8}{\epsilon _0}$
.
$\frac {8}{\epsilon _0}$
.
3 Proof of Theorem 1.3
Lemma 3.1 is crucial in the proof of Theorem 1.3. Before providing the proof, we introduce some notations first.
Notation
![]() $(\star ).$
Let
$(\star ).$
Let
![]() $X\ni x$
be a smooth surface germ, and let
$X\ni x$
be a smooth surface germ, and let
![]() $g: X_n\to X_{n-1}\to \cdots \to X_1\to X_0:=X$
be a sequence of blow-ups with the data
$g: X_n\to X_{n-1}\to \cdots \to X_1\to X_0:=X$
be a sequence of blow-ups with the data
![]() $(f_i,F_i,x_i\in X_i)$
. Let
$(f_i,F_i,x_i\in X_i)$
. Let
![]() $\mathcal {DG}$
be the dual graph of g, and assume that
$\mathcal {DG}$
be the dual graph of g, and assume that
![]() ${\mathcal {DG}}$
is a chain.
${\mathcal {DG}}$
is a chain.
Let
![]() $n_3\geq 2$
be the largest integer, such that
$n_3\geq 2$
be the largest integer, such that
![]() $x_i\in F_{i}\setminus F_{i-1}$
for any
$x_i\in F_{i}\setminus F_{i-1}$
for any
![]() $1\leq i\leq n_3-1$
, where we set
$1\leq i\leq n_3-1$
, where we set
![]() $F_0:=\emptyset $
. Let
$F_0:=\emptyset $
. Let
![]() $\{E_j\}_{-n_1\le j\le n_2}$
be the vertices of
$\{E_j\}_{-n_1\le j\le n_2}$
be the vertices of
![]() ${\mathcal {DG}}$
, such that
${\mathcal {DG}}$
, such that
![]() $E_0:=F_n$
is the only g-exceptional
$E_0:=F_n$
is the only g-exceptional
![]() $(-1)$
-curve on
$(-1)$
-curve on
![]() $X_n$
,
$X_n$
,
![]() $E_{n_2}:=F_1$
, and
$E_{n_2}:=F_1$
, and
![]() $E_i$
is adjacent to
$E_i$
is adjacent to
![]() $E_{i+1}$
for any
$E_{i+1}$
for any
![]() $-n_1\le i\le n_2-1$
(see Figure 2).
$-n_1\le i\le n_2-1$
(see Figure 2).

Figure 2 The dual graph of g.
We define
![]() $n_i(g):=n_i$
for
$n_i(g):=n_i$
for
![]() $1\le i\le 3$
,
$1\le i\le 3$
,
![]() $n(g)=n$
,
$n(g)=n$
,
![]() $w_j(g):=-E_j\cdot E_j$
for all j and
$w_j(g):=-E_j\cdot E_j$
for all j and
![]() $W_1(g):=\sum _{j<0}w_j(g)$
and
$W_1(g):=\sum _{j<0}w_j(g)$
and
![]() $W_2(g):=\sum _{j>0}w_j(g)$
.
$W_2(g):=\sum _{j>0}w_j(g)$
.
Lemma 3.1. With Notation
![]() $(\star )$
. Then:
$(\star )$
. Then:
In particular,
![]() $n(g)=n_1(g)+n_2(g)+1\leq n_3(g)+\min \{W_1(g),W_2(g)\}$
.
$n(g)=n_1(g)+n_2(g)+1\leq n_3(g)+\min \{W_1(g),W_2(g)\}$
.
Proof. For simplicity, let
![]() $n:=n(g)$
,
$n:=n(g)$
,
![]() $n_i:=n_i(g)$
for
$n_i:=n_i(g)$
for
![]() $1\le i\le 3$
,
$1\le i\le 3$
,
![]() $w_j:=w_j(g)=-E_j\cdot E_j$
for all j and
$w_j:=w_j(g)=-E_j\cdot E_j$
for all j and
![]() $W_j:=W_j(g)$
for
$W_j:=W_j(g)$
for
![]() $j=1,2$
.
$j=1,2$
.
We prove (3.1) by induction on the nonnegative integer
![]() $n-n_3$
.
$n-n_3$
.
If
![]() $n=n_3$
, then
$n=n_3$
, then
![]() $n_1=W_1=0$
,
$n_1=W_1=0$
,
![]() $n_2=n_3-1$
and
$n_2=n_3-1$
and
![]() $W_2=2n_3-2$
, thus, (3.1) holds (see Figure 3). If
$W_2=2n_3-2$
, thus, (3.1) holds (see Figure 3). If
![]() $n=n_3+1$
, then
$n=n_3+1$
, then
![]() $x_{n_3}\in F_{n_3}\cap F_{n_3-1}$
. In this case,
$x_{n_3}\in F_{n_3}\cap F_{n_3-1}$
. In this case,
![]() $n_1=1$
,
$n_1=1$
,
![]() $W_1=2$
,
$W_1=2$
,
![]() $n_2=n_3-1$
and
$n_2=n_3-1$
and
![]() $W_2=2n_3-1$
, thus, (3.1) holds (see Figure 3).
$W_2=2n_3-1$
, thus, (3.1) holds (see Figure 3).

Figure 3 The dual graph for the case
![]() $n=n_3$
and
$n=n_3$
and
![]() $n=n_3+1$
.
$n=n_3+1$
.
In general, suppose (3.1) holds for any sequence of blow-ups g, as in Notation
![]() $(\star )$
with positive integers
$(\star )$
with positive integers
![]() $n,n_3$
satisfying
$n,n_3$
satisfying
![]() $1\leq n-n_3\leq k$
. For the case when
$1\leq n-n_3\leq k$
. For the case when
![]() $n-n_3=k+1$
, we may contract the
$n-n_3=k+1$
, we may contract the
![]() $(-1)$
-curve on
$(-1)$
-curve on
![]() $X_n$
, and consider
$X_n$
, and consider
![]() $g':X_{n-1}\to \cdots \to X_0:= X$
, a subsequence of blow-ups of g with the data
$g':X_{n-1}\to \cdots \to X_0:= X$
, a subsequence of blow-ups of g with the data
![]() $(f_i,F_i,x_i\in X_i)$
for
$(f_i,F_i,x_i\in X_i)$
for
![]() $0\leq i\leq n-1$
. Denote
$0\leq i\leq n-1$
. Denote
![]() $n_i':=n_i(g')$
for any
$n_i':=n_i(g')$
for any
![]() $1\le i\le 3$
, and
$1\le i\le 3$
, and
![]() $W_j':=W_j(g')$
for any
$W_j':=W_j(g')$
for any
![]() $1\le j\le 2$
. By Lemma 2.14(1), either
$1\le j\le 2$
. By Lemma 2.14(1), either
![]() $w_{-1}=2$
or
$w_{-1}=2$
or
![]() $w_1$
=2. In the former case,
$w_1$
=2. In the former case,
![]() $W_1'=W_1-2, W_2'=W_2-1, n_1'=n_1-1$
,
$W_1'=W_1-2, W_2'=W_2-1, n_1'=n_1-1$
,
![]() $n_2'=n_2$
and
$n_2'=n_2$
and
![]() $n_3'=n_3$
. In the latter case,
$n_3'=n_3$
. In the latter case,
![]() $W_1'=W_1-1, W_2'=W_2-2, n_1'=n_1,n_2'=n_2-1$
and
$W_1'=W_1-1, W_2'=W_2-2, n_1'=n_1,n_2'=n_2-1$
and
![]() $n_3'=n_3$
. In both cases, by induction,
$n_3'=n_3$
. In both cases, by induction,
Hence, we finish the induction, and (3.1) is proved.
Since
![]() $w_j\geq 2$
for
$w_j\geq 2$
for
![]() $j\neq 0$
, we have
$j\neq 0$
, we have
![]() $W_1=\sum _{-n_1\leq j\leq -1} w_j\geq 2n_1$
and
$W_1=\sum _{-n_1\leq j\leq -1} w_j\geq 2n_1$
and
![]() $W_2=\sum _{1\leq j\leq n_2} w_j\geq 2n_2$
. By (3.1),
$W_2=\sum _{1\leq j\leq n_2} w_j\geq 2n_2$
. By (3.1),
and
which imply that
![]() $n=n_1+n_2+1\le n_3+\min \{W_1,W_2\}$
.
$n=n_1+n_2+1\le n_3+\min \{W_1,W_2\}$
.
We will need Lemma 3.2 to prove Theorems 1.3 and 1.4.
Lemma 3.2. Let
![]() $\gamma \in (0,1]$
be a real number. Let
$\gamma \in (0,1]$
be a real number. Let
![]() $N_0:= \lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor ,$
then we have the following.
$N_0:= \lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor ,$
then we have the following.
Let
![]() $(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, such that
$(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, such that
![]() $X\ni x$
is smooth and
$X\ni x$
is smooth and
![]() $B_i$
are distinct prime divisors. Suppose that
$B_i$
are distinct prime divisors. Suppose that
![]() $\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Let Y be a smooth surface and
$\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Let Y be a smooth surface and
![]() $f: Y\to X\ni x$
be a birational morphism with the dual graph
$f: Y\to X\ni x$
be a birational morphism with the dual graph
![]() ${\mathcal {DG}}$
, such that:
${\mathcal {DG}}$
, such that:
-
•
 $K_Y+B_Y=f^*(K_X+B)$
for some
$K_Y+B_Y=f^*(K_X+B)$
for some
 $B_Y\geq 0$
on Y,
$B_Y\geq 0$
on Y, -
•
 ${\mathcal {DG}}$
is a chain that contains only one
${\mathcal {DG}}$
is a chain that contains only one
 $(-1)$
-curve
$(-1)$
-curve
 $E_0$
,
$E_0$
, -
•
 $E_0$
is adjacent to two vertices of
$E_0$
is adjacent to two vertices of
 ${\mathcal {DG}}$
and
${\mathcal {DG}}$
and -
• either
 $E_0$
is the only vertex of
$E_0$
is the only vertex of
 ${\mathcal {DG}}$
, such that
${\mathcal {DG}}$
, such that
 $a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
, or
$a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
, or
 $a(E_0,X,B)=\mathrm {mld}(X\ni x, B)>0$
and
$a(E_0,X,B)=\mathrm {mld}(X\ni x, B)>0$
and
 $\sum _i n_i b_i\neq 1$
for all
$\sum _i n_i b_i\neq 1$
for all
 $n_i\in \mathbb {Z}_{\geq 0}$
.
$n_i\in \mathbb {Z}_{\geq 0}$
.
Then the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $N_0$
.
$N_0$
.
Proof. By Lemma 2.5,
![]() $b_i\geq \gamma $
for all i.
$b_i\geq \gamma $
for all i.
If
![]() $\mathrm {mld}(X\ni x, B)\geq \frac {\gamma }{2}$
, then by Lemma 2.21 with
$\mathrm {mld}(X\ni x, B)\geq \frac {\gamma }{2}$
, then by Lemma 2.21 with
![]() $\epsilon _0=\frac {\gamma }{2}$
, the number of vertices of
$\epsilon _0=\frac {\gamma }{2}$
, the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $\frac {16}{\gamma }$
.
$\frac {16}{\gamma }$
.
Thus, we may assume that
![]() $0\leq \mathrm {mld}(X\ni x,B)\leq \frac {\gamma }{2}$
. We may index the vertices of
$0\leq \mathrm {mld}(X\ni x,B)\leq \frac {\gamma }{2}$
. We may index the vertices of
![]() ${\mathcal {DG}}$
as
${\mathcal {DG}}$
as
![]() $\{E_j\}_{-n_1\leq j\leq n_2}$
for some positive integer
$\{E_j\}_{-n_1\leq j\leq n_2}$
for some positive integer
![]() $n_1,n_2$
, where
$n_1,n_2$
, where
![]() $E_j$
is adjacent to
$E_j$
is adjacent to
![]() $E_{j+1}$
for
$E_{j+1}$
for
![]() $-n_1\leq j\leq n_2-1$
. Let
$-n_1\leq j\leq n_2-1$
. Let
![]() $w_j:=-E_j\cdot E_j$
and
$w_j:=-E_j\cdot E_j$
and
![]() $a_j:=a(E_j,X\ni x, B)$
for all j.
$a_j:=a(E_j,X\ni x, B)$
for all j.
For all
![]() $-n_1\leq k\leq n_2$
, we have:
$-n_1\leq k\leq n_2$
, we have:
 $$ \begin{align} \left(K_Y+f^{-1}_* B+\sum_j (1-a_j)E_j\right)\cdot E_k=f^*(K_X+B)\cdot E_k=0. \end{align} $$
$$ \begin{align} \left(K_Y+f^{-1}_* B+\sum_j (1-a_j)E_j\right)\cdot E_k=f^*(K_X+B)\cdot E_k=0. \end{align} $$
Let
![]() $k=0$
, (3.2) becomes
$k=0$
, (3.2) becomes
![]() $0=-2+f^{-1}_* B\cdot E_0+(1-a_{-1})+(1-a_1)+w_0a_0$
, thus:
$0=-2+f^{-1}_* B\cdot E_0+(1-a_{-1})+(1-a_1)+w_0a_0$
, thus:
By the last assumption in the lemma, either
![]() $(a_{-1}-a_0)+(a_1-a_0)>0$
or
$(a_{-1}-a_0)+(a_1-a_0)>0$
or
![]() $a_0>0$
, thus,
$a_0>0$
, thus,
![]() $f_*^{-1}B\cdot E_0>0$
in both cases. Hence,
$f_*^{-1}B\cdot E_0>0$
in both cases. Hence,
![]() $f_*^{-1}B\cdot E_0-a_0\geq \gamma -\frac {\gamma }{2}=\frac {\gamma }{2}$
. Possibly switching
$f_*^{-1}B\cdot E_0-a_0\geq \gamma -\frac {\gamma }{2}=\frac {\gamma }{2}$
. Possibly switching
![]() $E_j (j<0)$
with
$E_j (j<0)$
with
![]() $E_j (j>0)$
, we may assume that
$E_j (j>0)$
, we may assume that
![]() $a_{-1}-a_0\geq \frac {\gamma }{4}$
.
$a_{-1}-a_0\geq \frac {\gamma }{4}$
.
By Lemma 2.13(2),
![]() $a_{-j}-a_{-j+1}\geq a_{-1}-a_0\geq \frac {\gamma }{4}$
for
$a_{-j}-a_{-j+1}\geq a_{-1}-a_0\geq \frac {\gamma }{4}$
for
![]() $1\leq j\leq n_1$
, thus,
$1\leq j\leq n_1$
, thus,
![]() $n_1\cdot \frac {\gamma }{4}\leq a_{-n_1}\leq 1$
, and
$n_1\cdot \frac {\gamma }{4}\leq a_{-n_1}\leq 1$
, and
![]() $n_1\leq \frac {4}{\gamma }$
. Since
$n_1\leq \frac {4}{\gamma }$
. Since
![]() $a_j\geq \frac {\gamma }{4}$
for all
$a_j\geq \frac {\gamma }{4}$
for all
![]() $-n_1\leq j\leq -1$
, by Lemma 2.13(1),
$-n_1\leq j\leq -1$
, by Lemma 2.13(1),
![]() $w_j\leq \frac {8}{\gamma }$
for all
$w_j\leq \frac {8}{\gamma }$
for all
![]() $-n_1\leq j\leq -1$
. Thus,
$-n_1\leq j\leq -1$
. Thus,
![]() $\sum _{j=-1}^{-n_1} w_j\leq n_1\cdot \frac {8}{\gamma }\leq \frac {32}{\gamma ^2}$
. Note that
$\sum _{j=-1}^{-n_1} w_j\leq n_1\cdot \frac {8}{\gamma }\leq \frac {32}{\gamma ^2}$
. Note that
![]() $X\ni x$
is smooth and
$X\ni x$
is smooth and
![]() ${\mathcal {DG}}$
has only one
${\mathcal {DG}}$
has only one
![]() $(-1)$
-curve, thus,
$(-1)$
-curve, thus,
![]() $f: Y\to X$
is a sequence of blow-ups as in Definition 2.16. Moreover,
$f: Y\to X$
is a sequence of blow-ups as in Definition 2.16. Moreover,
![]() ${\mathcal {DG}}$
is a chain, thus, by Lemma 3.1,
${\mathcal {DG}}$
is a chain, thus, by Lemma 3.1,
![]() $1+n_1+n_2\le n_3+\frac {32}{\gamma ^2}$
, where
$1+n_1+n_2\le n_3+\frac {32}{\gamma ^2}$
, where
![]() $n_3=n_3(f)$
is defined as in Notation
$n_3=n_3(f)$
is defined as in Notation
![]() $(\star )$
.
$(\star )$
.
It suffices to show that
![]() $n_3$
is bounded, we may assume that
$n_3$
is bounded, we may assume that
![]() $n_3>2$
. By the definition of
$n_3>2$
. By the definition of
![]() $n_3$
, there exists a sequence of blow-ups
$n_3$
, there exists a sequence of blow-ups
![]() $X_{n_3}\to \ldots X_1\to X_0:=X$
with the data
$X_{n_3}\to \ldots X_1\to X_0:=X$
with the data
![]() $(f_i,F_i,x_i\in X_i)$
, such that
$(f_i,F_i,x_i\in X_i)$
, such that
![]() $x_i\in F_i\setminus F_{i-1}$
for any
$x_i\in F_i\setminus F_{i-1}$
for any
![]() $1\leq i\leq n_3-1$
. Here,
$1\leq i\leq n_3-1$
. Here,
![]() $F_0:=\emptyset $
.
$F_0:=\emptyset $
.
Let
![]() $B_{X_i}$
be the strict transform of B on
$B_{X_i}$
be the strict transform of B on
![]() $X_i$
for
$X_i$
for
![]() $0\leq i\leq n_3$
, and let
$0\leq i\leq n_3$
, and let
![]() $a_i':=a(F_i,X,B)$
for
$a_i':=a(F_i,X,B)$
for
![]() $1\leq i\leq n_3$
, and
$1\leq i\leq n_3$
, and
![]() $a_0':=1$
. Since
$a_0':=1$
. Since
![]() $x_i\in F_i\setminus F_{i-1}$
,
$x_i\in F_i\setminus F_{i-1}$
,
![]() $a_{i}'-a_{i+1}'=\mathrm {mult}_{x_i}B_{X_i}-1$
for any
$a_{i}'-a_{i+1}'=\mathrm {mult}_{x_i}B_{X_i}-1$
for any
![]() $n_3-1\ge i\ge 0$
. By Lemma 2.13(2),
$n_3-1\ge i\ge 0$
. By Lemma 2.13(2),
![]() $a_{i}'-a_{i+1}'\geq \min \{a_1-a_0, a_{-1}-a_0\}\geq 0$
for
$a_{i}'-a_{i+1}'\geq \min \{a_1-a_0, a_{-1}-a_0\}\geq 0$
for
![]() $1\leq i\leq n_3-2$
(see Figure 2). Thus, by the last assumption in the lemma, either
$1\leq i\leq n_3-2$
(see Figure 2). Thus, by the last assumption in the lemma, either
![]() $\min \{a_1-a_0, a_{-1}-a_0\}>0$
or
$\min \{a_1-a_0, a_{-1}-a_0\}>0$
or
![]() $\mathrm {mult}_{x_i}B_{X_i}-1>0$
, in both cases, we have
$\mathrm {mult}_{x_i}B_{X_i}-1>0$
, in both cases, we have
![]() $a_{i}'-a_{i+1}'=\mathrm {mult}_{x_i}B_{X_i}-1>0$
. Hence,
$a_{i}'-a_{i+1}'=\mathrm {mult}_{x_i}B_{X_i}-1>0$
. Hence,
![]() $a_{i}'-a_{i+1}'=\mathrm {mult}_{x_i}B_{X_i}-1\geq \gamma $
for any
$a_{i}'-a_{i+1}'=\mathrm {mult}_{x_i}B_{X_i}-1\geq \gamma $
for any
![]() $1\leq i\leq n_3-2$
as
$1\leq i\leq n_3-2$
as
![]() $\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Therefore,
$\{\sum _i n_ib_i-1> 0\mid n_i\in \mathbb {Z}_{\geq 0}\}\subseteq [\gamma ,+\infty )$
. Therefore,
 $$ \begin{align*}0\leq a_{n_3-1}'=a_0'+\sum_{i=0}^{n_3-2}(a_{i+1}'-a_i')\leq 1-(n_3-1)\gamma,\end{align*} $$
$$ \begin{align*}0\leq a_{n_3-1}'=a_0'+\sum_{i=0}^{n_3-2}(a_{i+1}'-a_i')\leq 1-(n_3-1)\gamma,\end{align*} $$
and
![]() $n_3\leq 1+\frac {1}{\gamma }$
.
$n_3\leq 1+\frac {1}{\gamma }$
.
To sum up, the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
.
$\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
.
Now we are ready to prove Theorem 1.3.
Proof of Theorem 1.3
By Lemma 2.17, we may assume that
![]() $\mathrm {mld}(X\ni x, B)\leq 1$
.
$\mathrm {mld}(X\ni x, B)\leq 1$
.
Let
![]() $f: Y\to X\ni x$
be the birational morphism constructed in Lemma 2.20 with the dual graph
$f: Y\to X\ni x$
be the birational morphism constructed in Lemma 2.20 with the dual graph
![]() ${\mathcal {DG}}$
. We claim that the number of vertices of
${\mathcal {DG}}$
. We claim that the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $N_0:= \lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
.
$N_0:= \lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
.
Assume the claim holds, then by Lemma 2.18,
![]() $a(E,X,0)\leq 2^{N_0}$
for some exceptional divisor E, such that
$a(E,X,0)\leq 2^{N_0}$
for some exceptional divisor E, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni X,B)$
, we are done. It suffices to show the claim.
$a(E,X,B)=\mathrm {mld}(X\ni X,B)$
, we are done. It suffices to show the claim.
If the f-exceptional
![]() $(-1)$
-curve is adjacent to only one vertex of
$(-1)$
-curve is adjacent to only one vertex of
![]() ${\mathcal {DG}}$
, then by Lemma 2.15(1), the number of vertices of
${\mathcal {DG}}$
, then by Lemma 2.15(1), the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $ 1+\frac {1}{\gamma }$
.
$ 1+\frac {1}{\gamma }$
.
If the f-exceptional
![]() $(-1)$
-curve is adjacent to two vertices of
$(-1)$
-curve is adjacent to two vertices of
![]() ${\mathcal {DG}}$
, then by Lemma 3.2, the number of vertices of
${\mathcal {DG}}$
, then by Lemma 3.2, the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
. Thus, we finish the proof.
$\lfloor 1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }\rfloor $
. Thus, we finish the proof.
To end this section, we provide an example which shows that Theorem 1.3 does not hold if we do not assume that
![]() $\{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\geq 0}\}$
is bounded from below by a positive real number.
$\{\sum _i n_ib_i-1>0\mid n_i\in \mathbb {Z}_{\geq 0}\}$
is bounded from below by a positive real number.
Example 3.3. Let
![]() $\{(\mathbf {A}^2\ni 0, B_k)\}_{k\geq 2}$
be a sequence of klt surface germs, such that
$\{(\mathbf {A}^2\ni 0, B_k)\}_{k\geq 2}$
be a sequence of klt surface germs, such that
![]() $B_k:=\frac {1}{2}B_{k,1}+(\frac {1}{2}+\frac {1}{k+1})B_{k,2}$
, and
$B_k:=\frac {1}{2}B_{k,1}+(\frac {1}{2}+\frac {1}{k+1})B_{k,2}$
, and
![]() $B_{k,1}$
(respectively,
$B_{k,1}$
(respectively,
![]() $B_{k,2}$
) is defined by the equation
$B_{k,2}$
) is defined by the equation
![]() $x=0$
(respectively,
$x=0$
(respectively,
![]() $x-y^k=0$
) at
$x-y^k=0$
) at
![]() $0\in \mathbf {A}^2$
.
$0\in \mathbf {A}^2$
.
For each k, we may construct a sequence of blow-ups
![]() $X_{k}\to X_{k-1}\to \cdots \to X_{1}\to X_{0}:=X$
with the data
$X_{k}\to X_{k-1}\to \cdots \to X_{1}\to X_{0}:=X$
with the data
![]() $(f_i,F_i,x_i\in X_i)$
, such that
$(f_i,F_i,x_i\in X_i)$
, such that
![]() $x_{i-1}\in F_{i-1}$
is the intersection of the strict transforms of
$x_{i-1}\in F_{i-1}$
is the intersection of the strict transforms of
![]() $B_{k,1}$
and
$B_{k,1}$
and
![]() $B_{k,2}$
on
$B_{k,2}$
on
![]() $F_{i-1}$
for
$F_{i-1}$
for
![]() $1\le i\le k$
. Let
$1\le i\le k$
. Let
![]() $g_k: X_k\to X$
be the natural morphism induced by
$g_k: X_k\to X$
be the natural morphism induced by
![]() $\{f_i\}_{1\leq i\leq k}$
, we have
$\{f_i\}_{1\leq i\leq k}$
, we have
![]() $K_{X_k}+B_{X_k}=g_k^*(K_X+B_k)$
for some snc divisor
$K_{X_k}+B_{X_k}=g_k^*(K_X+B_k)$
for some snc divisor
![]() $B_{X_k}\geq 0$
on
$B_{X_k}\geq 0$
on
![]() $X_k$
, and the coefficients of
$X_k$
, and the coefficients of
![]() $B_{X_k}$
are no more than
$B_{X_k}$
are no more than
![]() $\frac {k}{k+1}$
. Thus, we will need at least k blow-ups as constructed above to extract an exceptional divisor
$\frac {k}{k+1}$
. Thus, we will need at least k blow-ups as constructed above to extract an exceptional divisor
![]() $F_k$
, such that
$F_k$
, such that
![]() $a(F_k,\mathbf {A}^2,B_k)=\mathrm {mld}(\mathbf {A}^2\ni 0, B_k)=\frac {1}{k+1}$
, and
$a(F_k,\mathbf {A}^2,B_k)=\mathrm {mld}(\mathbf {A}^2\ni 0, B_k)=\frac {1}{k+1}$
, and
![]() $a(F_k, \mathbf {A}^2,0)\geq k$
.
$a(F_k, \mathbf {A}^2,0)\geq k$
.
4 Proof of Theorem 1.2
Proof of Theorem 1.2
We may assume that
![]() ${\Gamma }\setminus \{0\}\neq \emptyset $
.
${\Gamma }\setminus \{0\}\neq \emptyset $
.
Let
![]() $(X\ni x, B)$
be an lc surface germ with
$(X\ni x, B)$
be an lc surface germ with
![]() $B\in {\Gamma }$
. By Lemma 2.17, we may assume that
$B\in {\Gamma }$
. By Lemma 2.17, we may assume that
![]() $\mathrm {mld}(X\ni x, B)\leq 1$
. By Theorem 1.3, it suffices to show the case when
$\mathrm {mld}(X\ni x, B)\leq 1$
. By Theorem 1.3, it suffices to show the case when
![]() $X\ni x$
is not smooth.
$X\ni x$
is not smooth.
If
![]() $\mathrm {mld}(X\ni x, B)=\operatorname {pld}(X\ni x, B)$
, then
$\mathrm {mld}(X\ni x, B)=\operatorname {pld}(X\ni x, B)$
, then
![]() $a(E,X,0)\leq 1$
for some prime divisor E over
$a(E,X,0)\leq 1$
for some prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x, B)$
. So we may assume that
$a(E,X,B)=\mathrm {mld}(X\ni x, B)$
. So we may assume that
![]() $\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
.
$\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
.
By Lemma 2.20, there exists a birational morphism
![]() $f: Y\to X\ni x$
which satisfies Lemma 2.20(1)–(5). Let
$f: Y\to X\ni x$
which satisfies Lemma 2.20(1)–(5). Let
![]() $\widetilde {f}:\widetilde {X}\to X$
be the minimal resolution of
$\widetilde {f}:\widetilde {X}\to X$
be the minimal resolution of
![]() $X\ni x$
,
$X\ni x$
,
![]() $g: Y\to \widetilde {X}\ni \widetilde {x}$
the birational morphism, such that
$g: Y\to \widetilde {X}\ni \widetilde {x}$
the birational morphism, such that
![]() $\widetilde {f}\circ g=f$
, where
$\widetilde {f}\circ g=f$
, where
![]() $\widetilde {x}\in \widetilde {X}$
is chosen as in Lemma 2.20(5), and there exists an
$\widetilde {x}\in \widetilde {X}$
is chosen as in Lemma 2.20(5), and there exists an
![]() $\widetilde {f}$
-exceptional prime divisor
$\widetilde {f}$
-exceptional prime divisor
![]() $\widetilde {E}$
over
$\widetilde {E}$
over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(\widetilde {E},X,B)=\operatorname {pld}(X\ni x, B)$
and
$a(\widetilde {E},X,B)=\operatorname {pld}(X\ni x, B)$
and
![]() $\widetilde {x}\in \widetilde {E}$
. Moreover, there is at most one other vertex
$\widetilde {x}\in \widetilde {E}$
. Moreover, there is at most one other vertex
![]() $\widetilde {E'}$
of
$\widetilde {E'}$
of
![]() $\widetilde {{\mathcal {DG}}}$
, such that
$\widetilde {{\mathcal {DG}}}$
, such that
![]() $\widetilde {x}\in \widetilde {E'}$
.
$\widetilde {x}\in \widetilde {E'}$
.
Let
![]() $\widetilde {{\mathcal {DG}}}$
be the dual graph of
$\widetilde {{\mathcal {DG}}}$
be the dual graph of
![]() $\widetilde {f}$
and
$\widetilde {f}$
and
![]() $\{F_i\}_{-n_1\leq i\leq n_2}$
the vertices of
$\{F_i\}_{-n_1\leq i\leq n_2}$
the vertices of
![]() $\widetilde {{\mathcal {DG}}}$
, such that
$\widetilde {{\mathcal {DG}}}$
, such that
![]() $n_1,n_2\in \mathbb {Z}_{\geq 0}$
,
$n_1,n_2\in \mathbb {Z}_{\geq 0}$
,
![]() $F_i$
is adjacent to
$F_i$
is adjacent to
![]() $F_{i+1}$
,
$F_{i+1}$
,
![]() $w_i:=-F_i\cdot F_i, a_i:=a(F_i,X,B)$
for all i, and
$w_i:=-F_i\cdot F_i, a_i:=a(F_i,X,B)$
for all i, and
![]() $F_0:=\widetilde {E}, F_1:=\widetilde {E'}$
(see Figure 4). We may write
$F_0:=\widetilde {E}, F_1:=\widetilde {E'}$
(see Figure 4). We may write
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
, where
$K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
, where
![]() $B_{\widetilde {X}}:=\widetilde {f}^{-1}_*{B}+\sum _i (1-a_i)F_i$
, and we define
$B_{\widetilde {X}}:=\widetilde {f}^{-1}_*{B}+\sum _i (1-a_i)F_i$
, and we define
![]() $\widetilde {B}:=\widetilde {f}^{-1}_*{B}+\sum _{\widetilde {x}\in F_i} (1-a_i)F_i$
.
$\widetilde {B}:=\widetilde {f}^{-1}_*{B}+\sum _{\widetilde {x}\in F_i} (1-a_i)F_i$
.

Figure 4 Cases when
![]() $\widetilde {x}\in F_0\cap F_1$
and when
$\widetilde {x}\in F_0\cap F_1$
and when
![]() $\widetilde {x}\notin F_i$
for
$\widetilde {x}\notin F_i$
for
![]() $i\neq 0$
.
$i\neq 0$
.
If
![]() $\widetilde {x}\notin F_i$
for all
$\widetilde {x}\notin F_i$
for all
![]() $i\neq 0$
, then we consider the surface germ
$i\neq 0$
, then we consider the surface germ
![]() $(\widetilde {X}\ni \widetilde {x}, \widetilde {B}=\widetilde {f}^{-1}_* B+(1-a_0)F_0)$
, where
$(\widetilde {X}\ni \widetilde {x}, \widetilde {B}=\widetilde {f}^{-1}_* B+(1-a_0)F_0)$
, where
![]() $\widetilde {B}\in {\Gamma }':={\Gamma }\cup \{1-a\mid a\in \mathrm {Pld}(2,{\Gamma })\}$
. By Lemma 2.9,
$\widetilde {B}\in {\Gamma }':={\Gamma }\cup \{1-a\mid a\in \mathrm {Pld}(2,{\Gamma })\}$
. By Lemma 2.9,
![]() ${\Gamma }'$
satisfies the DCC. Thus, by Theorem 1.3, we may find a positive integer
${\Gamma }'$
satisfies the DCC. Thus, by Theorem 1.3, we may find a positive integer
![]() $N_1$
which only depends on
$N_1$
which only depends on
![]() ${\Gamma }$
, and a prime divisor E over
${\Gamma }$
, and a prime divisor E over
![]() $\widetilde {X}\ni \widetilde {x}$
, such that
$\widetilde {X}\ni \widetilde {x}$
, such that
![]() $a(E,\widetilde {X}, \widetilde {B})=a(E,X,B)=\mathrm {mld}(X\ni x,B)$
, and
$a(E,\widetilde {X}, \widetilde {B})=a(E,X,B)=\mathrm {mld}(X\ni x,B)$
, and
![]() $a(E,X,0)\leq a(E,\widetilde {X},0)\leq N_1$
.
$a(E,X,0)\leq a(E,\widetilde {X},0)\leq N_1$
.
So we may assume that
![]() $\widetilde {x}=F_0\cap F_1$
. By Lemma 2.4, there exist positive real numbers
$\widetilde {x}=F_0\cap F_1$
. By Lemma 2.4, there exist positive real numbers
![]() $\epsilon ,\delta \leq 1$
depending only on
$\epsilon ,\delta \leq 1$
depending only on
![]() ${\Gamma }$
, such that
${\Gamma }$
, such that
![]() $\{\sum _i n_ib_i-1>0\mid b_i\in {\Gamma }^{\prime }_{\epsilon }\cap [0,1], n_i\in \mathbb {Z}_{\ge 0}\}\subseteq [\delta ,+\infty )$
. Recall that
$\{\sum _i n_ib_i-1>0\mid b_i\in {\Gamma }^{\prime }_{\epsilon }\cap [0,1], n_i\in \mathbb {Z}_{\ge 0}\}\subseteq [\delta ,+\infty )$
. Recall that
![]() ${\Gamma }^{\prime }_\epsilon =\cup _{b'\in {\Gamma }'} [b'-\epsilon , b']$
.
${\Gamma }^{\prime }_\epsilon =\cup _{b'\in {\Gamma }'} [b'-\epsilon , b']$
.
If
![]() $a_1-a_0\leq \epsilon $
, then we consider the surface germ
$a_1-a_0\leq \epsilon $
, then we consider the surface germ
![]() $(\widetilde {X}\ni \widetilde {x},\widetilde {B}=\widetilde {f}^{-1}_*B+(1-a_0)F_0+(1-a_1)F_1)$
, where
$(\widetilde {X}\ni \widetilde {x},\widetilde {B}=\widetilde {f}^{-1}_*B+(1-a_0)F_0+(1-a_1)F_1)$
, where
![]() $\widetilde {B}\in {\Gamma }^{\prime }_{\epsilon }\cap [0,1]$
. By Theorem 1.3, there exist a positive integer
$\widetilde {B}\in {\Gamma }^{\prime }_{\epsilon }\cap [0,1]$
. By Theorem 1.3, there exist a positive integer
![]() $N_2$
which only depends on
$N_2$
which only depends on
![]() ${\Gamma }$
, and a prime divisor E over
${\Gamma }$
, and a prime divisor E over
![]() $\widetilde {X}\ni \widetilde {x}$
, such that
$\widetilde {X}\ni \widetilde {x}$
, such that
![]() $a(E,\widetilde {X}, \widetilde {B})=a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
$a(E,\widetilde {X}, \widetilde {B})=a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
![]() $a(E,X,0)\leq a(E,\widetilde {X},0)\le N_2$
.
$a(E,X,0)\leq a(E,\widetilde {X},0)\le N_2$
.
If
![]() $a_1-a_0\geq \epsilon $
, then we claim that there exists a DCC set
$a_1-a_0\geq \epsilon $
, then we claim that there exists a DCC set
![]() ${\Gamma }''$
depending only on
${\Gamma }''$
depending only on
![]() ${\Gamma }$
, such that
${\Gamma }$
, such that
![]() $1-a_1\in {\Gamma }''$
.
$1-a_1\in {\Gamma }''$
.

Figure 5 Cases when
![]() $a_1-a_0\geq \epsilon $
.
$a_1-a_0\geq \epsilon $
.
Assume the claim holds, then we consider the surface germ
![]() $(\widetilde {X}\ni \widetilde {x},\widetilde {B}=\widetilde {f}^{-1}_*B+(1-a_0)F_0+(1-a_1)F_1)$
, where
$(\widetilde {X}\ni \widetilde {x},\widetilde {B}=\widetilde {f}^{-1}_*B+(1-a_0)F_0+(1-a_1)F_1)$
, where
![]() $\widetilde {B}\in {\Gamma }''\cup {\Gamma }'$
. By Theorem 1.3, we may find a positive integer
$\widetilde {B}\in {\Gamma }''\cup {\Gamma }'$
. By Theorem 1.3, we may find a positive integer
![]() $N_3$
which only depends on
$N_3$
which only depends on
![]() ${\Gamma }$
, and a prime divisor E over
${\Gamma }$
, and a prime divisor E over
![]() $\widetilde {X}\ni \widetilde {x}$
, such that
$\widetilde {X}\ni \widetilde {x}$
, such that
![]() $a(E,\widetilde {X}, \widetilde {B})=a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
$a(E,\widetilde {X}, \widetilde {B})=a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
![]() $a(E,X,0)\leq a(E,\widetilde {X},0)\le N_3$
. Let
$a(E,X,0)\leq a(E,\widetilde {X},0)\le N_3$
. Let
![]() $N:=\max \{N_1,N_2,N_3\}$
, and we are done.
$N:=\max \{N_1,N_2,N_3\}$
, and we are done.
It suffices to show the claim. By Lemma 2.13(1),
![]() $w_i\leq \frac {2}{\epsilon }$
for any
$w_i\leq \frac {2}{\epsilon }$
for any
![]() $0<i\leq n_2$
. Since
$0<i\leq n_2$
. Since
![]() $1\geq a_{n_2}=a_0+\sum _{i=0}^{n_2-1} (a_{i+1}-a_i)\geq n_2\epsilon $
,
$1\geq a_{n_2}=a_0+\sum _{i=0}^{n_2-1} (a_{i+1}-a_i)\geq n_2\epsilon $
,
![]() $n_2\leq \frac {1}{\epsilon }$
. We may write:
$n_2\leq \frac {1}{\epsilon }$
. We may write:
For each
![]() $1\leq j\leq n_2$
, we have:
$1\leq j\leq n_2$
, we have:
which implies
![]() $\sum _{-n_1\leq i\leq n_2} (a_i-1)F_i\cdot F_j=-{F_j}^2-2+{\widetilde {f}}^{-1}_{*}B \cdot F_j$
, or equivalently,
$\sum _{-n_1\leq i\leq n_2} (a_i-1)F_i\cdot F_j=-{F_j}^2-2+{\widetilde {f}}^{-1}_{*}B \cdot F_j$
, or equivalently,
 $$ \begin{align*}\begin{pmatrix} F_1\cdot F_1&\cdots &F_{n_2}\cdot F_1 \\ \vdots&\ddots & \vdots \\ F_1\cdot F_{n_2}&\cdots &F_{n_2}\cdot F_{n_2} \\ \end{pmatrix} \begin{pmatrix} a_1-1 \\ \vdots \\ a_{n_2}-1 \\ \end{pmatrix} = \begin{pmatrix} w_{1}-2+\widetilde{f}^{-1}_*B\cdot F_1+(1-a_0)\\ \vdots\\ w_{n_2}-2+\widetilde{f}^{-1}_*B\cdot F_{n_2}\\ \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} F_1\cdot F_1&\cdots &F_{n_2}\cdot F_1 \\ \vdots&\ddots & \vdots \\ F_1\cdot F_{n_2}&\cdots &F_{n_2}\cdot F_{n_2} \\ \end{pmatrix} \begin{pmatrix} a_1-1 \\ \vdots \\ a_{n_2}-1 \\ \end{pmatrix} = \begin{pmatrix} w_{1}-2+\widetilde{f}^{-1}_*B\cdot F_1+(1-a_0)\\ \vdots\\ w_{n_2}-2+\widetilde{f}^{-1}_*B\cdot F_{n_2}\\ \end{pmatrix}.\end{align*} $$
By assumption,
![]() $w_j-2+\widetilde {f}^{-1}_*B\cdot F_j$
belongs to a DCC set, and by Lemma 2.9,
$w_j-2+\widetilde {f}^{-1}_*B\cdot F_j$
belongs to a DCC set, and by Lemma 2.9,
![]() $1-a_0$
belongs to the DCC set
$1-a_0$
belongs to the DCC set
![]() $\{1-a\mid a\in \mathrm {Pld}(2,{\Gamma })\}$
.
$\{1-a\mid a\in \mathrm {Pld}(2,{\Gamma })\}$
.
By [Reference Kollár and Mori15, Lemma 3.40],
![]() $(F_i\cdot F_j)_{1\le i,j\le n_2}$
is a negative definite matrix. Let
$(F_i\cdot F_j)_{1\le i,j\le n_2}$
is a negative definite matrix. Let
![]() $(s_{ij})_{n_2\times n_2}$
be the inverse matrix of
$(s_{ij})_{n_2\times n_2}$
be the inverse matrix of
![]() $(F_i\cdot F_j)_{1\le i,j\le n_2}$
. By [Reference Kollár and Mori15, Lemma 3.41],
$(F_i\cdot F_j)_{1\le i,j\le n_2}$
. By [Reference Kollár and Mori15, Lemma 3.41],
![]() $s_{ij}<0$
for any
$s_{ij}<0$
for any
![]() $1\le i,j\le n_2$
, thus:
$1\le i,j\le n_2$
, thus:
 $$ \begin{align*}1-a_1=-s_{11}(w_{1}-2+\widetilde{f}^{-1}_*B\cdot F_1+(1-a_0))-\sum_{j=2}^{n_2}s_{1j}(w_j-2+\widetilde{f}^{-1}_*B\cdot F_j)\end{align*} $$
$$ \begin{align*}1-a_1=-s_{11}(w_{1}-2+\widetilde{f}^{-1}_*B\cdot F_1+(1-a_0))-\sum_{j=2}^{n_2}s_{1j}(w_j-2+\widetilde{f}^{-1}_*B\cdot F_j)\end{align*} $$
belongs to a DCC set.
5 Proof of Theorem 1.4
In this section, we will first show Theorem 1.4, then we will generalise Theorems 1.3 and 1.4 (see Theorems 5.4 and 5.5).
Lemma 5.1. Let
![]() $(X\ni x, B:=\sum _i b_iB_i)$
be an lc surface germ, where
$(X\ni x, B:=\sum _i b_iB_i)$
be an lc surface germ, where
![]() $B_i$
are distinct prime divisors. Let
$B_i$
are distinct prime divisors. Let
![]() $h: W\to X\ni x$
be a log resolution of
$h: W\to X\ni x$
be a log resolution of
![]() $(X\ni x,B)$
, and let
$(X\ni x,B)$
, and let
![]() $S=\{E_j\}$
be a finite set of valuations of h-exceptional prime divisors, such that
$S=\{E_j\}$
be a finite set of valuations of h-exceptional prime divisors, such that
![]() $a(E_j,X,B)=\mathrm {mld} (X\ni x, B)$
for all j. Suppose that
$a(E_j,X,B)=\mathrm {mld} (X\ni x, B)$
for all j. Suppose that
![]() $\sum _i n_ib_i\neq 1$
for any
$\sum _i n_ib_i\neq 1$
for any
![]() $n_i\in \mathbb {Z}_{\geq 0}$
,
$n_i\in \mathbb {Z}_{\geq 0}$
,
![]() $\mathrm {mld}(X\ni x, B)\in (0,1]$
, and
$\mathrm {mld}(X\ni x, B)\in (0,1]$
, and
![]() $E_j$
is exceptional over
$E_j$
is exceptional over
![]() $\tilde {X}$
for some j, where
$\tilde {X}$
for some j, where
![]() $\tilde {X}\to X$
is the minimal resolution of
$\tilde {X}\to X$
is the minimal resolution of
![]() $X\ni x$
. Then there exist a smooth surface Y and a birational morphism
$X\ni x$
. Then there exist a smooth surface Y and a birational morphism
![]() $f: Y\to X\ni x$
with the dual graph
$f: Y\to X\ni x$
with the dual graph
![]() ${\mathcal {DG}}$
, such that:
${\mathcal {DG}}$
, such that:
-
(1)
 $K_Y+B_Y=f^*(K_X+B)$
for some
$K_Y+B_Y=f^*(K_X+B)$
for some
 $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
 $B_Y\geq 0$
on Y,
$B_Y\geq 0$
on Y, -
(2) each valuation in S corresponds to some vertex of
 ${\mathcal {DG}}$
,
${\mathcal {DG}}$
, -
(3)
 ${\mathcal {DG}}$
contains only one
${\mathcal {DG}}$
contains only one
 $(-1)$
-curve
$(-1)$
-curve
 $E_0$
, and it corresponds to a valuation in S and
$E_0$
, and it corresponds to a valuation in S and -
(4)
 ${\mathcal {DG}}$
is a chain.
${\mathcal {DG}}$
is a chain.
Proof. By Lemma 2.19, there exist a smooth surface Y and a birational morphism
![]() $f:Y\to X\ni x$
with the dual graph of
$f:Y\to X\ni x$
with the dual graph of
![]() ${\mathcal {DG}}$
which satisfy (1)–(2), and each f-exceptional
${\mathcal {DG}}$
which satisfy (1)–(2), and each f-exceptional
![]() $(-1)$
-curve corresponds to some valuation in S.
$(-1)$
-curve corresponds to some valuation in S.
For (3), by the assumption on S,
![]() ${\mathcal {DG}}$
contains at least one
${\mathcal {DG}}$
contains at least one
![]() $(-1)$
-curve
$(-1)$
-curve
![]() $E_0$
. If there exist two
$E_0$
. If there exist two
![]() $(-1)$
-curves
$(-1)$
-curves
![]() $E_0'\neq E_0$
, then
$E_0'\neq E_0$
, then
![]() $a(E_0,X,B)=a(E_0',X,B)=\mathrm {mld}(X\ni x, B)>0$
by construction, and there exists a set of distinct vertices
$a(E_0,X,B)=a(E_0',X,B)=\mathrm {mld}(X\ni x, B)>0$
by construction, and there exists a set of distinct vertices
![]() $\{C_k\}_{0\leq k \leq n}$
of
$\{C_k\}_{0\leq k \leq n}$
of
![]() ${\mathcal {DG}}$
, such that
${\mathcal {DG}}$
, such that
![]() $n\ge 2$
,
$n\ge 2$
,
![]() $C_{n}:=E_0'$
,
$C_{n}:=E_0'$
,
![]() $C_0$
is a
$C_0$
is a
![]() $(-1)$
-curve,
$(-1)$
-curve,
![]() $-C_k\cdot C_k\ge -2$
for
$-C_k\cdot C_k\ge -2$
for
![]() $1\le k\le n-1$
and
$1\le k\le n-1$
and
![]() $C_k$
is adjacent to
$C_k$
is adjacent to
![]() $C_{k+1}$
for
$C_{k+1}$
for
![]() $0\leq k\leq n-1$
. Since
$0\leq k\leq n-1$
. Since
![]() $a(C_0,X,B)=a(C_{n},X,B)=\mathrm {mld}(X\ni x, B)>0$
, by Lemma 2.13(6),
$a(C_0,X,B)=a(C_{n},X,B)=\mathrm {mld}(X\ni x, B)>0$
, by Lemma 2.13(6),
![]() $-C_k\cdot C_k=2$
for
$-C_k\cdot C_k=2$
for
![]() $1\leq k\leq n-1$
. Let
$1\leq k\leq n-1$
. Let
![]() $E:=\sum _{k=0}^{n} C_k$
, then
$E:=\sum _{k=0}^{n} C_k$
, then
![]() $E\cdot E=0$
, which contradicts the negativity lemma.
$E\cdot E=0$
, which contradicts the negativity lemma.
For (4), suppose that
![]() ${\mathcal {DG}}$
contains a fork F. Since
${\mathcal {DG}}$
contains a fork F. Since
![]() $E_0$
is a
$E_0$
is a
![]() $(-1)$
-curve, by Lemma 2.14(2),
$(-1)$
-curve, by Lemma 2.14(2),
![]() $E_0\neq F$
. By (3) and (5) of Lemma 2.13, we have
$E_0\neq F$
. By (3) and (5) of Lemma 2.13, we have
![]() $a(E_0,X,B)\geq a(F,X,B)\geq \mathrm {mld}(X\ni x, B)$
, thus,
$a(E_0,X,B)\geq a(F,X,B)\geq \mathrm {mld}(X\ni x, B)$
, thus,
![]() $a(E_0,X,B)= a(F,X,B)=\mathrm {mld}(X\ni x, B)>0$
. There exists a set of distinct vertices
$a(E_0,X,B)= a(F,X,B)=\mathrm {mld}(X\ni x, B)>0$
. There exists a set of distinct vertices
![]() $\{C_i'\}_{0\leq i\leq m}$
, such that
$\{C_i'\}_{0\leq i\leq m}$
, such that
![]() $C_0':=E_0$
,
$C_0':=E_0$
,
![]() $C_m':= F$
, and
$C_m':= F$
, and
![]() $C_i'$
is adjacent to
$C_i'$
is adjacent to
![]() $C_{i+1}'$
for
$C_{i+1}'$
for
![]() $0\leq i\leq m-1$
. We may denote
$0\leq i\leq m-1$
. We may denote
![]() $w_i':=-C_i'\cdot C_i'$
and
$w_i':=-C_i'\cdot C_i'$
and
![]() $a_i':=a(C_i',X,B)$
for
$a_i':=a(C_i',X,B)$
for
![]() $0\leq i\leq m$
. By Lemma 2.13(6), we have
$0\leq i\leq m$
. By Lemma 2.13(6), we have
![]() $a_0'=\cdots =a_m'$
, and
$a_0'=\cdots =a_m'$
, and
![]() $w_k'=2$
for
$w_k'=2$
for
![]() $1\leq k\leq m-1$
. Since
$1\leq k\leq m-1$
. Since
![]() $C_{m}'$
is a fork and
$C_{m}'$
is a fork and
![]() $a_{m-1}'=a_m'$
, by Lemma 2.13(3),
$a_{m-1}'=a_m'$
, by Lemma 2.13(3),
![]() $w_m'=2$
.
$w_m'=2$
.
If
![]() $C_0'$
is adjacent to only one vertex of
$C_0'$
is adjacent to only one vertex of
![]() ${\mathcal {DG}}$
, which is
${\mathcal {DG}}$
, which is
![]() $C_1'$
by our construction, then since
$C_1'$
by our construction, then since
![]() $\sum _i n_ib_i\neq 1$
for any
$\sum _i n_ib_i\neq 1$
for any
![]() $n_i\in \mathbb {Z}_{\geq 0}$
,
$n_i\in \mathbb {Z}_{\geq 0}$
,
![]() $a_0'\neq a_1'$
by Lemma 2.15(2), a contradiction.
$a_0'\neq a_1'$
by Lemma 2.15(2), a contradiction.

Figure 6
![]() $C_0'$
is adjacent to
$C_0'$
is adjacent to
![]() $C_{-1}'$
and
$C_{-1}'$
and
![]() $C_1'$
.
$C_1'$
.
Thus, we may assume that
![]() $C_0'$
is adjacent to a vertex
$C_0'$
is adjacent to a vertex
![]() $C_{-1}'$
of
$C_{-1}'$
of
![]() ${\mathcal {DG}}$
other than
${\mathcal {DG}}$
other than
![]() $C_1'$
(see Figure 6). We may contract
$C_1'$
(see Figure 6). We may contract
![]() $C_k'$
for
$C_k'$
for
![]() $0\leq k\leq m-1$
step by step, and will end up with a fork which is a
$0\leq k\leq m-1$
step by step, and will end up with a fork which is a
![]() $(-1)$
-curve, this contradicts Lemma 2.14(2).
$(-1)$
-curve, this contradicts Lemma 2.14(2).
Lemma 5.2. Let
![]() $(X\ni x, B:=\sum _i b_iB_i)$
be an lc surface germ, where
$(X\ni x, B:=\sum _i b_iB_i)$
be an lc surface germ, where
![]() $B_i$
are distinct prime divisors. Suppose that
$B_i$
are distinct prime divisors. Suppose that
![]() $X\ni x$
is a klt surface germ,
$X\ni x$
is a klt surface germ,
![]() $\mathrm {mld}(X\ni x, B)=0$
, and
$\mathrm {mld}(X\ni x, B)=0$
, and
![]() $\sum _i n_ib_i\neq 1$
for any
$\sum _i n_ib_i\neq 1$
for any
![]() $n_i\in \mathbb {Z}_{\ge 0}$
. Then there is only one prime divisor E over
$n_i\in \mathbb {Z}_{\ge 0}$
. Then there is only one prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=0$
.
$a(E,X,B)=0$
.
Proof. By [Reference Birkar2, Lemma 2.7] (this holds for surfaces in any characteristic), we can find a plt blow up
![]() $g: Y\to X\ni x$
, such that:
$g: Y\to X\ni x$
, such that:
-
•
 $K_Y+B_Y=g^*(K_X+B)$
for some
$K_Y+B_Y=g^*(K_X+B)$
for some
 $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
 $B_Y\geq 0$
on Y,
$B_Y\geq 0$
on Y, -
• there is only one g-exceptional prime divisor E,
-
•
 $\operatorname {Supp} E\subseteq \lfloor B_Y \rfloor $
and
$\operatorname {Supp} E\subseteq \lfloor B_Y \rfloor $
and -
•
 $(Y, E)$
is plt.
$(Y, E)$
is plt.
Since the relative Kawamata-Viehweg vanishing theorem holds for birational morphisms between surfaces in any characteristic (see [Reference Tanaka23, Theorem 0.5]), by a similar argument as in [Reference Hacon and Xu10, Proposition 4.1], E is normal. By the adjunction formula ([Reference Shokurov20, §3], [14, §16]),
![]() $K_E+B_E:=(K_Y+B_Y)|_E$
, where:
$K_E+B_E:=(K_Y+B_Y)|_E$
, where:
 $$ \begin{align*}B_E=\sum_i \frac{m_i-1+\sum_j n_{i,j}b_j}{m_i}p_i\end{align*} $$
$$ \begin{align*}B_E=\sum_i \frac{m_i-1+\sum_j n_{i,j}b_j}{m_i}p_i\end{align*} $$
for some distinct closed points
![]() $p_i$
on E and some
$p_i$
on E and some
![]() $m_i\in \mathbb {Z}_{>0}$
and
$m_i\in \mathbb {Z}_{>0}$
and
![]() $n_{i,j}\in \mathbb {Z}_{\geq 0}$
, such that
$n_{i,j}\in \mathbb {Z}_{\geq 0}$
, such that
![]() $\sum _j n_{i,j} b_j\leq 1$
for all i. By assumption,
$\sum _j n_{i,j} b_j\leq 1$
for all i. By assumption,
![]() $\sum _j n_{i,j} b_j\neq 1$
, thus,
$\sum _j n_{i,j} b_j\neq 1$
, thus,
![]() $\sum _j n_{i,j} b_j< 1$
for all i, which implies
$\sum _j n_{i,j} b_j< 1$
for all i, which implies
![]() $\lfloor B_E \rfloor =0$
, thus,
$\lfloor B_E \rfloor =0$
, thus,
![]() $(E, B_E)$
is klt. By the inversion of adjunction for surfaces (which is well known in any characteristic),
$(E, B_E)$
is klt. By the inversion of adjunction for surfaces (which is well known in any characteristic),
![]() $(Y, B_Y)$
is plt, and we are done.
$(Y, B_Y)$
is plt, and we are done.
Proof of Theorem 1.4
By Lemma 2.17, we may assume that
![]() $\mathrm {mld}(X\ni x, B)\leq 1$
.
$\mathrm {mld}(X\ni x, B)\leq 1$
.
If
![]() $\mathrm {mld}(X\ni x, B)=0$
, since
$\mathrm {mld}(X\ni x, B)=0$
, since
![]() $X\ni x$
is smooth, then by Lemma 5.2, there exists a unique prime divisor E over
$X\ni x$
is smooth, then by Lemma 5.2, there exists a unique prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=0$
. By Theorem 1.3,
$a(E,X,B)=0$
. By Theorem 1.3,
![]() $a(E,X,0)\leq 2^{N_0}$
. Thus, we may assume that
$a(E,X,0)\leq 2^{N_0}$
. Thus, we may assume that
![]() $\mathrm {mld}(X\ni x, B)>0$
.
$\mathrm {mld}(X\ni x, B)>0$
.
We may apply Lemma 5.1 to S, there exist a smooth surface Y and a birational morphism
![]() $f: Y\to X\ni x$
with the dual graph
$f: Y\to X\ni x$
with the dual graph
![]() ${\mathcal {DG}}$
, which satisfy Lemma 5.1(1)–(4). Let
${\mathcal {DG}}$
, which satisfy Lemma 5.1(1)–(4). Let
![]() $E_0$
be the unique
$E_0$
be the unique
![]() $(-1)$
-curve in
$(-1)$
-curve in
![]() ${\mathcal {DG}}$
. It suffices to give an upper bound for the number of vertices of
${\mathcal {DG}}$
. It suffices to give an upper bound for the number of vertices of
![]() ${\mathcal {DG}}$
.
${\mathcal {DG}}$
.
If
![]() $E_0$
is adjacent to only one vertex of
$E_0$
is adjacent to only one vertex of
![]() ${\mathcal {DG}}$
, then by Lemma 2.15(2)–(3), the number of vertices of
${\mathcal {DG}}$
, then by Lemma 2.15(2)–(3), the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $1+\frac {1}{\gamma }$
, and
$1+\frac {1}{\gamma }$
, and
![]() $|S|=1$
.
$|S|=1$
.
If
![]() $E_0$
is adjacent to two vertices of
$E_0$
is adjacent to two vertices of
![]() ${\mathcal {DG}}$
, then by Lemma 3.2, the number of vertices of
${\mathcal {DG}}$
, then by Lemma 3.2, the number of vertices of
![]() ${\mathcal {DG}}$
is bounded from above by
${\mathcal {DG}}$
is bounded from above by
![]() $1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }$
. Thus,
$1+\frac {32}{\gamma ^2}+\frac {1}{\gamma }$
. Thus,
![]() $|S|\leq N_0$
, and by Lemma 2.18,
$|S|\leq N_0$
, and by Lemma 2.18,
![]() $a(E,X,0)\le 2^{N_0}$
for any
$a(E,X,0)\le 2^{N_0}$
for any
![]() $E\in S$
.
$E\in S$
.
Now we are going to introduce and prove Theorems 5.4 and 5.5. First, we need to introduce the following definition.
Definition 5.3. Let
![]() $X\ni x$
be a klt surface germ. Let
$X\ni x$
be a klt surface germ. Let
![]() $\widetilde {f}: \widetilde {X}\to X\ni x$
be the minimal resolution and
$\widetilde {f}: \widetilde {X}\to X\ni x$
be the minimal resolution and
![]() $\{E_i\}_{1\leq i\leq n}$
the set of
$\{E_i\}_{1\leq i\leq n}$
the set of
![]() $\widetilde {f}$
-exceptional prime divisors. The determinant of
$\widetilde {f}$
-exceptional prime divisors. The determinant of
![]() $X\ni x$
is defined by:
$X\ni x$
is defined by:
 $$ \begin{align*}\det(X\ni x):=\left\{ \begin{array}{lcl} |\mathrm{det} (E_i\cdot E_j)_{1\leq i,j\leq n}| &{\text{if }x\in X \text{ is a singular point,}}\\ 1 &{\text{if }x\in X \text{ is a smooth point.}} \end{array} \right.\end{align*} $$
$$ \begin{align*}\det(X\ni x):=\left\{ \begin{array}{lcl} |\mathrm{det} (E_i\cdot E_j)_{1\leq i,j\leq n}| &{\text{if }x\in X \text{ is a singular point,}}\\ 1 &{\text{if }x\in X \text{ is a smooth point.}} \end{array} \right.\end{align*} $$
Theorem 5.4. Let
![]() $\gamma \in (0,1]$
be a real number and I a positive integer. Then
$\gamma \in (0,1]$
be a real number and I a positive integer. Then
![]() $N_0:=\lfloor 1+\frac {32I^2}{\gamma ^2}+\frac {I}{\gamma }\rfloor $
satisfies the following.
$N_0:=\lfloor 1+\frac {32I^2}{\gamma ^2}+\frac {I}{\gamma }\rfloor $
satisfies the following.
Let
![]() $(X\ni x,B:=\sum _{i} b_iB_i)$
be an lc surface germ, where
$(X\ni x,B:=\sum _{i} b_iB_i)$
be an lc surface germ, where
![]() $B_i$
are distinct prime divisors. Suppose that
$B_i$
are distinct prime divisors. Suppose that
![]() $\det (X\ni x)\mid I$
, and
$\det (X\ni x)\mid I$
, and
![]() $\{\sum _i n_ib_i-t>0\mid n_i\in \mathbb {Z}_{\geq 0}, t\in \mathbb {Z}\cap [1,I]\}\subseteq [\gamma ,+\infty )$
. Then there exists a prime divisor E over
$\{\sum _i n_ib_i-t>0\mid n_i\in \mathbb {Z}_{\geq 0}, t\in \mathbb {Z}\cap [1,I]\}\subseteq [\gamma ,+\infty )$
. Then there exists a prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
$a(E,X,B)=\mathrm {mld}(X\ni x,B)$
and
![]() $a(E,X,0)\leq 2^{N_0}$
.
$a(E,X,0)\leq 2^{N_0}$
.
Theorem 5.5. Let
![]() $\gamma \in (0,1]$
be a real number and
$\gamma \in (0,1]$
be a real number and
![]() $X\ni x$
a klt surface germ. Let N be the number of vertices of the dual graph of the minimal resolution of
$X\ni x$
a klt surface germ. Let N be the number of vertices of the dual graph of the minimal resolution of
![]() $X\ni x$
and
$X\ni x$
and
![]() $I:=\det (X\ni x)$
. Then
$I:=\det (X\ni x)$
. Then
![]() $N_0:=\lfloor 1+\frac {32I^2}{\gamma ^2}+\frac {I}{\gamma }\rfloor +N$
satisfies the following.
$N_0:=\lfloor 1+\frac {32I^2}{\gamma ^2}+\frac {I}{\gamma }\rfloor +N$
satisfies the following.
Let
![]() $(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
$(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
![]() $B_i$
are distinct prime divisors. Let
$B_i$
are distinct prime divisors. Let
![]() $S:=\{E\mid E\text { is a prime divisor over } X\ni x, a(E,X,B)=\mathrm {mld}(X\ni x,B)\}$
. Suppose that
$S:=\{E\mid E\text { is a prime divisor over } X\ni x, a(E,X,B)=\mathrm {mld}(X\ni x,B)\}$
. Suppose that
![]() $\{\sum _i n_ib_i-t\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}, t\in \mathbb {Z}\cap [1,I]\}\subseteq [\gamma ,+\infty )$
. Then
$\{\sum _i n_ib_i-t\geq 0\mid n_i\in \mathbb {Z}_{\geq 0}, t\in \mathbb {Z}\cap [1,I]\}\subseteq [\gamma ,+\infty )$
. Then
![]() $|S|\le N_0$
, and
$|S|\le N_0$
, and
![]() $a(E,X,0)\le 2^{N_0}$
for any
$a(E,X,0)\le 2^{N_0}$
for any
![]() $E\in S$
.
$E\in S$
.
Remark 5.6. It is easy to see that Theorem 5.5 does not hold if
![]() $X\ni x$
is not klt. Also it does not hold if we only bound
$X\ni x$
is not klt. Also it does not hold if we only bound
![]() $\det (X\ni x)$
as in Theorem 5.4 (see Example 5.9).
$\det (X\ni x)$
as in Theorem 5.4 (see Example 5.9).
Theorem 5.4 follows from Theorem 1.3, and Theorem 5.5 follows from Theorems 1.4 and 5.4. We will need the following lemma to prove the above theorems.
Lemma 5.7. Let
![]() $(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
$(X\ni x,B:=\sum _i b_iB_i)$
be an lc surface germ, where
![]() $B_i$
are distinct prime divisors. Let
$B_i$
are distinct prime divisors. Let
![]() $\widetilde {f}: \widetilde {X}\to X\ni x$
be the minimal resolution, and we may write
$\widetilde {f}: \widetilde {X}\to X\ni x$
be the minimal resolution, and we may write
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
for some
$K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
for some
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $B_{\widetilde {X}}:=\sum _j \widetilde {b_j}\widetilde {B_j}\geq 0$
, where
$B_{\widetilde {X}}:=\sum _j \widetilde {b_j}\widetilde {B_j}\geq 0$
, where
![]() $\widetilde {B_j}$
are distinct prime divisors on
$\widetilde {B_j}$
are distinct prime divisors on
![]() $\widetilde {X}$
. Let
$\widetilde {X}$
. Let
![]() $I\in \mathbb {Z}_{>0}$
, such that
$I\in \mathbb {Z}_{>0}$
, such that
![]() $\det (X\ni x)\mid I$
, then:
$\det (X\ni x)\mid I$
, then:
-
(1)
 $\{\sum _j n_j'\widetilde {b_j}-1>0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t>0 \mid n_i\in \mathbb {Z}_{\geq 0}, t\leq I\}$
and
$\{\sum _j n_j'\widetilde {b_j}-1>0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t>0 \mid n_i\in \mathbb {Z}_{\geq 0}, t\leq I\}$
and -
(2)
 $\{\sum _j n_j'\widetilde {b_j}-1\geq 0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t\ge 0 \mid n_i\in \mathbb {Z}_{\geq 0},\sum _i n_i>0, t\leq I\}$
.
$\{\sum _j n_j'\widetilde {b_j}-1\geq 0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t\ge 0 \mid n_i\in \mathbb {Z}_{\geq 0},\sum _i n_i>0, t\leq I\}$
.
Proof. Let
![]() ${\mathcal {DG}}$
be the dual graph of
${\mathcal {DG}}$
be the dual graph of
![]() $\widetilde {f}$
. Let
$\widetilde {f}$
. Let
![]() $\{E_i\}_{1 \leq i\leq m}$
be the set of
$\{E_i\}_{1 \leq i\leq m}$
be the set of
![]() $\widetilde {f}$
-exceptional divisors and
$\widetilde {f}$
-exceptional divisors and
![]() $w_i:=-E_i\cdot E_i$
,
$w_i:=-E_i\cdot E_i$
,
![]() $a_i:=a(E_i,X\ni x,B)$
for all i.
$a_i:=a(E_i,X\ni x,B)$
for all i.
For each
![]() $1\leq j\leq m$
,
$1\leq j\leq m$
,
![]() $(K_Y+f^{-1}_*B+\sum _{i=1}^m (1-a_i)E_i)\cdot E_{j}=0$
, which implies that
$(K_Y+f^{-1}_*B+\sum _{i=1}^m (1-a_i)E_i)\cdot E_{j}=0$
, which implies that
![]() $\sum _{i=1}^m (a_i-1)E_i\cdot E_{j}=-{E_{j}}^2-2+\widetilde {f}^{-1}_* B \cdot E_{j}$
.
$\sum _{i=1}^m (a_i-1)E_i\cdot E_{j}=-{E_{j}}^2-2+\widetilde {f}^{-1}_* B \cdot E_{j}$
.
By [Reference Kollár and Mori15, Lemma 3.40],
![]() $(E_i\cdot E_{j})_{1\le i,j\le m}$
is a negative definite matrix. Let
$(E_i\cdot E_{j})_{1\le i,j\le m}$
is a negative definite matrix. Let
![]() $(s_{ij})_{m\times m}$
be the inverse matrix of
$(s_{ij})_{m\times m}$
be the inverse matrix of
![]() $(E_i\cdot E_{j})_{1\le i,j\le m}$
. By [Reference Kollár and Mori15, Lemma 3.41] and the assumption on I, we have
$(E_i\cdot E_{j})_{1\le i,j\le m}$
. By [Reference Kollár and Mori15, Lemma 3.41] and the assumption on I, we have
![]() $Is_{ij}\in \mathbb {Z}_{<0}$
for
$Is_{ij}\in \mathbb {Z}_{<0}$
for
![]() $1\leq i,j\leq m$
. Thus, for all i,
$1\leq i,j\leq m$
. Thus, for all i,
 $$ \begin{align} 1-a_i=\frac{1}{I}\sum_{j=1}^m (-Is_{ij})\cdot(w_{j}-2+\widetilde{f}^{-1}_* B\cdot E_{j}). \end{align} $$
$$ \begin{align} 1-a_i=\frac{1}{I}\sum_{j=1}^m (-Is_{ij})\cdot(w_{j}-2+\widetilde{f}^{-1}_* B\cdot E_{j}). \end{align} $$
Since
![]() $w_{j}\geq 2$
for all j, (1) and (2) follow immediately from (5.1) and the equation
$w_{j}\geq 2$
for all j, (1) and (2) follow immediately from (5.1) and the equation
![]() $B_{\widetilde {X}}=\sum _j \widetilde {b_j}\widetilde {B_j}=\widetilde {f}^{-1}_* B+\sum _{i=1}^m (1-a_i)E_i$
.
$B_{\widetilde {X}}=\sum _j \widetilde {b_j}\widetilde {B_j}=\widetilde {f}^{-1}_* B+\sum _{i=1}^m (1-a_i)E_i$
.
Proof of Theorem 5.4
By Lemma 2.17, we may assume that
![]() $\mathrm {mld}(X\ni x, B)\leq 1$
.
$\mathrm {mld}(X\ni x, B)\leq 1$
.
If
![]() $\mathrm {mld}(X\ni x, B)=\operatorname {pld}(X\ni x, B)$
, then
$\mathrm {mld}(X\ni x, B)=\operatorname {pld}(X\ni x, B)$
, then
![]() $a(E,X,0)\leq 1$
for some prime divisor E over
$a(E,X,0)\leq 1$
for some prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=\mathrm {mld}(X\ni x, B)$
. So we may assume that
$a(E,X,B)=\mathrm {mld}(X\ni x, B)$
. So we may assume that
![]() $\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
.
$\mathrm {mld}(X\ni x, B)\neq \operatorname {pld}(X\ni x, B)$
.
By Lemma 2.20, there exists a birational morphism
![]() $f: Y\to X\ni x$
, which satisfies Lemma 2.20(1)–(4). Let
$f: Y\to X\ni x$
, which satisfies Lemma 2.20(1)–(4). Let
![]() $\widetilde {f}:\widetilde {X}\to X$
be the minimal resolution of
$\widetilde {f}:\widetilde {X}\to X$
be the minimal resolution of
![]() $X\ni x$
and
$X\ni x$
and
![]() $g: Y\to \widetilde {X}$
the natural morphism induced by f. We may write
$g: Y\to \widetilde {X}$
the natural morphism induced by f. We may write
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
for some
$K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
for some
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $B_{\widetilde {X}}:= \sum _j \widetilde {b_j}\widetilde {B_{j}}\ge 0$
on
$B_{\widetilde {X}}:= \sum _j \widetilde {b_j}\widetilde {B_{j}}\ge 0$
on
![]() $\widetilde {X}$
, where
$\widetilde {X}$
, where
![]() $\widetilde {B_j}$
are distinct prime divisors.
$\widetilde {B_j}$
are distinct prime divisors.
By Lemma 5.7(1), we have
![]() $\{\sum _j n_j'\widetilde {b_j}-1>0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t>0 \mid n_i\in \mathbb {Z}_{\geq 0}, t\leq I\}\subseteq [\frac {\gamma }{I},\infty )$
by the assumption. Since the dual graph
$\{\sum _j n_j'\widetilde {b_j}-1>0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t>0 \mid n_i\in \mathbb {Z}_{\geq 0}, t\leq I\}\subseteq [\frac {\gamma }{I},\infty )$
by the assumption. Since the dual graph
![]() ${\mathcal {DG}}$
of f contains only one
${\mathcal {DG}}$
of f contains only one
![]() $(-1)$
-curve, there exists a closed point
$(-1)$
-curve, there exists a closed point
![]() $\widetilde {x}\in \widetilde {X}$
, such that
$\widetilde {x}\in \widetilde {X}$
, such that
![]() $\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for any g-exceptional divisor E. Apply Theorem 1.3 to the surface germ
$\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for any g-exceptional divisor E. Apply Theorem 1.3 to the surface germ
![]() $(\widetilde {X}\ni \widetilde {x}, B_{\widetilde {X}})$
, we are done.
$(\widetilde {X}\ni \widetilde {x}, B_{\widetilde {X}})$
, we are done.
Proof of Theorem 5.5
By Lemma 2.17, we may assume that
![]() $\mathrm {mld}(X\ni x, B)\leq 1$
.
$\mathrm {mld}(X\ni x, B)\leq 1$
.
We may assume that
![]() $B\neq 0$
, otherwise, we may take
$B\neq 0$
, otherwise, we may take
![]() $\widetilde {f}:\widetilde {X}\to X\ni x$
as the minimal resolution, and
$\widetilde {f}:\widetilde {X}\to X\ni x$
as the minimal resolution, and
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*K_X$
, where
$K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*K_X$
, where
![]() $B_{\widetilde {X}}$
is an snc divisor. Since
$B_{\widetilde {X}}$
is an snc divisor. Since
![]() $X\ni x$
is klt, all elements in S are on
$X\ni x$
is klt, all elements in S are on
![]() $\widetilde {X}$
, thus,
$\widetilde {X}$
, thus,
![]() $|S|\leq N$
, and
$|S|\leq N$
, and
![]() $a(E,X,0)\leq 1$
for all
$a(E,X,0)\leq 1$
for all
![]() $E\in S$
. For the same reason, we may assume that not all elements of S are on the minimal resolution
$E\in S$
. For the same reason, we may assume that not all elements of S are on the minimal resolution
![]() $\widetilde {X}$
of
$\widetilde {X}$
of
![]() $X\ni x$
.
$X\ni x$
.
If
![]() $\mathrm {mld}(X\ni x, B)=0$
, then by Lemma 5.2, there exists a unique exceptional divisor E over
$\mathrm {mld}(X\ni x, B)=0$
, then by Lemma 5.2, there exists a unique exceptional divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)=0$
. By Theorem 5.4,
$a(E,X,B)=0$
. By Theorem 5.4,
![]() $a(E,X,0)\leq 2^{\lfloor 1+\frac {32{I^2}}{\gamma ^2}+\frac {I}{\gamma }\rfloor }$
. Thus, we may assume that
$a(E,X,0)\leq 2^{\lfloor 1+\frac {32{I^2}}{\gamma ^2}+\frac {I}{\gamma }\rfloor }$
. Thus, we may assume that
![]() $\mathrm {mld}(X\ni x, B)>0$
from now on. Since
$\mathrm {mld}(X\ni x, B)>0$
from now on. Since
![]() $\sum _i n_ib_i\neq 1$
for any
$\sum _i n_ib_i\neq 1$
for any
![]() $n_i\in \mathbb {Z}_{\ge 0}$
, we have
$n_i\in \mathbb {Z}_{\ge 0}$
, we have
![]() $\lfloor B\rfloor =0$
, and
$\lfloor B\rfloor =0$
, and
![]() $(X,B)$
is klt near
$(X,B)$
is klt near
![]() $x\in X$
, hence, by [Reference Kollár and Mori15, Proposition 2.36], S is a finite set.
$x\in X$
, hence, by [Reference Kollár and Mori15, Proposition 2.36], S is a finite set.
Now, we may apply Lemma 5.1 to the set S, there exists a birational morphism
![]() $f: Y\to X\ni x$
that satisfies Lemma 5.1(1)–(4). Let
$f: Y\to X\ni x$
that satisfies Lemma 5.1(1)–(4). Let
![]() $\widetilde {f}:\widetilde {X}\to X$
be the minimal resolution of
$\widetilde {f}:\widetilde {X}\to X$
be the minimal resolution of
![]() $X\ni x$
and
$X\ni x$
and
![]() $g: Y\to \widetilde {X}$
the natural morphism induced by f. We may write
$g: Y\to \widetilde {X}$
the natural morphism induced by f. We may write
![]() $K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
for some
$K_{\widetilde {X}}+B_{\widetilde {X}}=\widetilde {f}^*(K_X+B)$
for some
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $B_{\widetilde {X}}:= \sum _j \widetilde {b_j}\widetilde {B_{j}}\ge 0$
on
$B_{\widetilde {X}}:= \sum _j \widetilde {b_j}\widetilde {B_{j}}\ge 0$
on
![]() $\widetilde {X}$
, where
$\widetilde {X}$
, where
![]() $\widetilde {B_j}$
are distinct prime divisors on
$\widetilde {B_j}$
are distinct prime divisors on
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
By Lemma 5.7(2), we have
![]() $\{\sum _j n_j'\widetilde {b_j}-1\geq 0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t\geq 0 \mid n_i\in \mathbb {Z}_{\geq 0}, \sum _i n_i>0 ,t\leq I\}\subseteq [\frac {\gamma }{I},\infty )$
. Since the dual graph
$\{\sum _j n_j'\widetilde {b_j}-1\geq 0 \mid n_j'\in \mathbb {Z}_{\geq 0}\}\subseteq \frac {1}{I}\{\sum _i n_ib_i-t\geq 0 \mid n_i\in \mathbb {Z}_{\geq 0}, \sum _i n_i>0 ,t\leq I\}\subseteq [\frac {\gamma }{I},\infty )$
. Since the dual graph
![]() ${\mathcal {DG}}$
of f contains only one
${\mathcal {DG}}$
of f contains only one
![]() $(-1)$
-curve, there exists a closed point
$(-1)$
-curve, there exists a closed point
![]() $\widetilde {x}\in \widetilde {X}$
, such that
$\widetilde {x}\in \widetilde {X}$
, such that
![]() $\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for any g-exceptional divisor E. Apply Theorem 1.4 to the surface germ
$\operatorname {center}_{\widetilde {X}} E=\widetilde {x}$
for any g-exceptional divisor E. Apply Theorem 1.4 to the surface germ
![]() $(\widetilde {X}\ni \widetilde {x}, B_{\widetilde {X}})$
, we are done.
$(\widetilde {X}\ni \widetilde {x}, B_{\widetilde {X}})$
, we are done.
To end this section, we provide some examples.
The following example shows that Theorem 1.4 does not hold if
![]() $\sum _i n_i b_i=1$
for some
$\sum _i n_i b_i=1$
for some
![]() $n_i\in \mathbb {Z}_{\geq 0}$
.
$n_i\in \mathbb {Z}_{\geq 0}$
.
Example 5.8. Let
![]() $\{b_i\}_{1\leq i\leq m}\subseteq (0,1]$
, such that
$\{b_i\}_{1\leq i\leq m}\subseteq (0,1]$
, such that
![]() $\sum _{i=1}^m n_ib_i=1$
for some
$\sum _{i=1}^m n_ib_i=1$
for some
![]() $n_i\in \mathbb {Z}_{>0}$
.
$n_i\in \mathbb {Z}_{>0}$
.
Let
![]() $(X\ni x):=(\mathbf {A}^2\ni 0)$
,
$(X\ni x):=(\mathbf {A}^2\ni 0)$
,
![]() $D_{m,n}$
the Cartier divisor, which is defined by the equation
$D_{m,n}$
the Cartier divisor, which is defined by the equation
![]() $x-y^m-y^{m+n}=0$
and
$x-y^m-y^{m+n}=0$
and
![]() $B_k:=\sum _{i=1}^m b_i\sum _{j=1}^{n_i} D_{k+i,j}$
for any positive integer k, where
$B_k:=\sum _{i=1}^m b_i\sum _{j=1}^{n_i} D_{k+i,j}$
for any positive integer k, where
![]() $D_{k+i,j}$
is defined by
$D_{k+i,j}$
is defined by
![]() $x-y^{k+i}-y^{k+i+j}=0$
. Then
$x-y^{k+i}-y^{k+i+j}=0$
. Then
![]() $(X\ni x, B_k)$
is canonical near x for any k as
$(X\ni x, B_k)$
is canonical near x for any k as
![]() $\operatorname {mult}_{x}B_k\le 1$
.
$\operatorname {mult}_{x}B_k\le 1$
.
For each k, we may construct a sequence of blow-ups
![]() $X_{k}\to X_{k-1}\to \cdots \to X_{1}\to X_{0}:=X$
with the data
$X_{k}\to X_{k-1}\to \cdots \to X_{1}\to X_{0}:=X$
with the data
![]() $(f_i,F_i,x_i\in X_i)$
, such that
$(f_i,F_i,x_i\in X_i)$
, such that
![]() $x_{i-1}\in F_{i-1}$
is the intersection of the strict transforms of these
$x_{i-1}\in F_{i-1}$
is the intersection of the strict transforms of these
![]() $D_{k+i,j}$
on
$D_{k+i,j}$
on
![]() $F_{i-1}$
for all
$F_{i-1}$
for all
![]() $i,j$
. Then
$i,j$
. Then
![]() $a(F_i,X,B_k)=1=\mathrm {mld}(X\ni x, B_k)$
for any k and
$a(F_i,X,B_k)=1=\mathrm {mld}(X\ni x, B_k)$
for any k and
![]() $1\le i\le k$
. Thus, both
$1\le i\le k$
. Thus, both
![]() $|S_k|$
and
$|S_k|$
and
![]() $\sup _{E\in S_k}\{a(E,X,0)\}$
are not bounded from above as
$\sup _{E\in S_k}\{a(E,X,0)\}$
are not bounded from above as
![]() $|S_k|\geq k$
, and
$|S_k|\geq k$
, and
![]() $a(F_k,X,0)\ge k$
for each k.
$a(F_k,X,0)\ge k$
for each k.
The following example shows that Theorem 5.5 does not hold if we do not fix the germ, even when we bound the determinant of the surface germs.
Example 5.9. Let
![]() $\{(X_k\ni x_k)\}_{k\geq 1}$
be a sequence of surface germs, such that each
$\{(X_k\ni x_k)\}_{k\geq 1}$
be a sequence of surface germs, such that each
![]() $X_k\ni x_k$
is a Du Val singularity of type
$X_k\ni x_k$
is a Du Val singularity of type
![]() $D_{k+3}$
([Reference Kollár and Mori15, Theorem 4.22]). We have
$D_{k+3}$
([Reference Kollár and Mori15, Theorem 4.22]). We have
![]() $\det (X_k\ni x_k)=4$
for all
$\det (X_k\ni x_k)=4$
for all
![]() $k\geq 4$
, but
$k\geq 4$
, but
![]() $|S_k|=k+3$
for
$|S_k|=k+3$
for
![]() $k\geq 1$
is not bounded from above.
$k\geq 1$
is not bounded from above.
6 An equivalent conjecture for MLDs on a fixed germ
Definition 6.1. Let X be a normal variety and
![]() $B:=\sum b_iB_i$
an
$B:=\sum b_iB_i$
an
![]() $\mathbb {R}$
-divisor on X, where
$\mathbb {R}$
-divisor on X, where
![]() $B_i$
are distinct prime divisors. We define
$B_i$
are distinct prime divisors. We define
![]() $||B||:=\max _i\{|b_i|\}$
. Let E be a prime divisor over X and
$||B||:=\max _i\{|b_i|\}$
. Let E be a prime divisor over X and
![]() $Y\to X$
a birational model, such that E is on Y. We define
$Y\to X$
a birational model, such that E is on Y. We define
![]() $\operatorname {mult}_E B_i$
to be the multiplicity of the strict transform of
$\operatorname {mult}_E B_i$
to be the multiplicity of the strict transform of
![]() $B_i$
on Y along E for each i, and
$B_i$
on Y along E for each i, and
![]() $\operatorname {mult}_E B:=\sum _i b_i\operatorname {mult}_E B_i$
.
$\operatorname {mult}_E B:=\sum _i b_i\operatorname {mult}_E B_i$
.
Conjecture 6.2 could be regarded as an inversion of stability type conjecture for divisors which compute MLDs, see [Reference Birkar and Shokurov3, Main Proposition 2.1], [Reference Chen and Han5, Theorem 5.10] for other inversion of stability type results.
Conjecture 6.2. Let
![]() ${\Gamma }\subseteq [0,1]$
be a finite set, X a normal quasiprojective variety and
${\Gamma }\subseteq [0,1]$
be a finite set, X a normal quasiprojective variety and
![]() $x\in X$
a closed point. Then there exists a positive real number
$x\in X$
a closed point. Then there exists a positive real number
![]() $\tau $
depending only on
$\tau $
depending only on
![]() ${\Gamma }$
and
${\Gamma }$
and
![]() $x\in X$
satisfying the following.
$x\in X$
satisfying the following.
Assume that
![]() $(X\ni x,B)$
and
$(X\ni x,B)$
and
![]() $(X\ni x,B')$
are two lc germs, such that:
$(X\ni x,B')$
are two lc germs, such that:
-
(1)
 $B'\le B$
,
$B'\le B$
,
 $||B-B'||<\tau ,B\in {\Gamma }$
and
$||B-B'||<\tau ,B\in {\Gamma }$
and -
(2)
 $a(E,X,B')=\mathrm {mld}(X\ni x,B')$
for some prime divisor E over
$a(E,X,B')=\mathrm {mld}(X\ni x,B')$
for some prime divisor E over
 $X\ni x$
.
$X\ni x$
.
Then
![]() $a(E,X,B)=\mathrm {mld}(X\ni x,B)$
.
$a(E,X,B)=\mathrm {mld}(X\ni x,B)$
.
Conjecture 6.2 does not hold for surface germs
![]() $(X\ni x,B)$
, in general, if either
$(X\ni x,B)$
, in general, if either
![]() ${\Gamma }$
is a DCC set (see [Reference Han and Luo9, Example 7.5]) or we do not fix
${\Gamma }$
is a DCC set (see [Reference Han and Luo9, Example 7.5]) or we do not fix
![]() $X\ni x$
(see [Reference Han and Luo9, Example 7.6]).
$X\ni x$
(see [Reference Han and Luo9, Example 7.6]).
Proposition 6.3. For any fixed
![]() $\mathbb {Q}$
-Gorenstein germ
$\mathbb {Q}$
-Gorenstein germ
![]() $X\ni x$
over an algebraically closed field of characteristic zero, Conjecture 6.2 is equivalent to Conjecture 1.1, thus, Conjecture 6.2 is equivalent to the ACC conjecture for MLDs.
$X\ni x$
over an algebraically closed field of characteristic zero, Conjecture 6.2 is equivalent to Conjecture 1.1, thus, Conjecture 6.2 is equivalent to the ACC conjecture for MLDs.
Remark 6.4. We need to work in characteristic zero since we need to apply [Reference Kawakita12, Theorem 1.1].
Proof. Suppose that Conjecture 6.2 holds. Let
![]() $t:=\min \{1,\tau \}>0$
. Then
$t:=\min \{1,\tau \}>0$
. Then
![]() $||(1-t)B-B||<\tau $
. Let E be a prime divisor over
$||(1-t)B-B||<\tau $
. Let E be a prime divisor over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,(1-t)B)=\mathrm {mld}(X\ni x,(1-t)B)$
. Then:
$a(E,X,(1-t)B)=\mathrm {mld}(X\ni x,(1-t)B)$
. Then:
and
![]() $\operatorname {mult}_{E}B\le \frac {1}{t}\mathrm {mld}(X\ni x,0).$
$\operatorname {mult}_{E}B\le \frac {1}{t}\mathrm {mld}(X\ni x,0).$
By assumption,
![]() $\mathrm {mld}(X\ni x,0)\ge \mathrm {mld}(X\ni x,B)=a(E,X,B)=a(E,X,0)-\operatorname {mult}_{E}B$
. Hence:
$\mathrm {mld}(X\ni x,0)\ge \mathrm {mld}(X\ni x,B)=a(E,X,B)=a(E,X,0)-\operatorname {mult}_{E}B$
. Hence:
 $$ \begin{align*}a(E,X,0)\le \left(1+\frac{1}{t}\right)\mathrm{mld}(X\ni x,0),\end{align*} $$
$$ \begin{align*}a(E,X,0)\le \left(1+\frac{1}{t}\right)\mathrm{mld}(X\ni x,0),\end{align*} $$
and Conjecture 1.1 holds.
Suppose that Conjecture 1.1 holds, then there exists a positive real number N which only depends on
![]() ${\Gamma }$
and
${\Gamma }$
and
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E_0,X,0)\le N$
for some
$a(E_0,X,0)\le N$
for some
![]() $E_0$
satisfying
$E_0$
satisfying
![]() $a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
. In particular,
$a(E_0,X,B)=\mathrm {mld}(X\ni x,B)$
. In particular,
![]() $\operatorname {mult}_{E_0}B=-a(E_0,X,B)+a(E_0,X,0)\le N$
.
$\operatorname {mult}_{E_0}B=-a(E_0,X,B)+a(E_0,X,0)\le N$
.
By [Reference Kawakita12, Theorem 1.1], there exists a positive real number
![]() $\delta $
, which only depends on
$\delta $
, which only depends on
![]() ${\Gamma }$
and
${\Gamma }$
and
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B)\ge \mathrm {mld}(X\ni x,B)+\delta $
for any
$a(E,X,B)\ge \mathrm {mld}(X\ni x,B)+\delta $
for any
![]() $(X\ni x,B)$
and prime divisor E over
$(X\ni x,B)$
and prime divisor E over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $B\in {\Gamma }$
and
$B\in {\Gamma }$
and
![]() $a(E,X,B)>\mathrm {mld}(X\ni x,B)$
.
$a(E,X,B)>\mathrm {mld}(X\ni x,B)$
.
We may assume that
![]() ${\Gamma }\setminus \{0\}\neq \emptyset $
. Let
${\Gamma }\setminus \{0\}\neq \emptyset $
. Let
![]() $t:=\frac {\delta }{2N}$
and
$t:=\frac {\delta }{2N}$
and
![]() $\tau :=t\cdot \min \{{\Gamma }\setminus \{0\}\}$
. We claim that
$\tau :=t\cdot \min \{{\Gamma }\setminus \{0\}\}$
. We claim that
![]() $\tau $
has the required properties.
$\tau $
has the required properties.
For any
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() $B'$
, such that
$B'$
, such that
![]() $||B'-B||<\tau $
, we have
$||B'-B||<\tau $
, we have
![]() $B-B'<tB$
. Let E be a prime divisor over
$B-B'<tB$
. Let E be a prime divisor over
![]() $X\ni x$
, such that
$X\ni x$
, such that
![]() $a(E,X,B')=\mathrm {mld} (X\ni x,B')$
. Suppose that
$a(E,X,B')=\mathrm {mld} (X\ni x,B')$
. Suppose that
![]() $a(E,X,B)>\mathrm {mld}(X\ni x,B)$
. Then
$a(E,X,B)>\mathrm {mld}(X\ni x,B)$
. Then
![]() $a(E,X,B)\ge \mathrm {mld}(X\ni x,B)+\delta =a(E_0,X,B)+\delta $
. Thus:
$a(E,X,B)\ge \mathrm {mld}(X\ni x,B)+\delta =a(E_0,X,B)+\delta $
. Thus:
 $$ \begin{align*} a(E_0,X,0)-\operatorname{mult}_{E_0}B'&=a(E_0,X,B')\ge a(E,X,B')\ge a(E,X,B)\\ &\ge a(E_0,X,B)+\delta=a(E_0,X,0)-\operatorname{mult}_{E_0}B+\delta. \end{align*} $$
$$ \begin{align*} a(E_0,X,0)-\operatorname{mult}_{E_0}B'&=a(E_0,X,B')\ge a(E,X,B')\ge a(E,X,B)\\ &\ge a(E_0,X,B)+\delta=a(E_0,X,0)-\operatorname{mult}_{E_0}B+\delta. \end{align*} $$
Hence,
![]() $\delta \le \operatorname {mult}_{E_0}(B-B')\le t\operatorname {mult}_{E_0} B\le tN=\frac {\delta }{2},$
a contradiction.
$\delta \le \operatorname {mult}_{E_0}(B-B')\le t\operatorname {mult}_{E_0} B\le tN=\frac {\delta }{2},$
a contradiction.
Proposition 6.5. For any fixed
![]() $\mathbb {Q}$
-Gorenstein germ
$\mathbb {Q}$
-Gorenstein germ
![]() $X\ni x$
over an algebraically closed field of characteristic zero, Conjecture 1.1 implies Conjecture 6.2 holds for any DCC set
$X\ni x$
over an algebraically closed field of characteristic zero, Conjecture 1.1 implies Conjecture 6.2 holds for any DCC set
![]() ${\Gamma }$
when B has only one component.
${\Gamma }$
when B has only one component.
Proof. Otherwise, there exist two sequence of germs
![]() $\{(X\ni x,t_iB_i)\}_i$
and
$\{(X\ni x,t_iB_i)\}_i$
and
![]() $\{(X\ni x,t_i'B_i)\}_i$
, and prime divisors
$\{(X\ni x,t_i'B_i)\}_i$
, and prime divisors
![]() $E_i$
over
$E_i$
over
![]() $X\ni x$
, such that:
$X\ni x$
, such that:
-
• for each i,
 $B_i$
is a prime divisor on X,
$B_i$
is a prime divisor on X,
 $t_i\in {\Gamma }$
is increasing and
$t_i\in {\Gamma }$
is increasing and
 $t_i'<t_i$
,
$t_i'<t_i$
, -
•
 $t:=\lim _{i\to \infty } t_i=\lim _{i\to \infty }t_i'$
,
$t:=\lim _{i\to \infty } t_i=\lim _{i\to \infty }t_i'$
, -
•
 $a(E_i,X, t_i'B_i)=\mathrm {mld}(X\ni x, t_i'B_i)$
and
$a(E_i,X, t_i'B_i)=\mathrm {mld}(X\ni x, t_i'B_i)$
and -
•
 $a(E_i,X,t_iB_i)\neq \mathrm {mld} (X\ni x,t_iB_i)$
.
$a(E_i,X,t_iB_i)\neq \mathrm {mld} (X\ni x,t_iB_i)$
.
By Proposition 6.3, there exists a positive real number
![]() $\tau $
, which only depends on t and
$\tau $
, which only depends on t and
![]() $X\ni x$
, such that if
$X\ni x$
, such that if
![]() $|t-t_i'|<\tau $
, then
$|t-t_i'|<\tau $
, then
![]() $a(E_i,X,tB_i)=\mathrm {mld}(X\ni x,tB_i)$
. Since
$a(E_i,X,tB_i)=\mathrm {mld}(X\ni x,tB_i)$
. Since
![]() $a(E_i,X,t_{*}B_i)$
is a linear function with respect to the variable
$a(E_i,X,t_{*}B_i)$
is a linear function with respect to the variable
![]() $t_{*}$
, we have
$t_{*}$
, we have
![]() $a(E_i,X,t_iB_i)=\mathrm {mld}(X\ni x,t_iB_i)$
, a contradiction.
$a(E_i,X,t_iB_i)=\mathrm {mld}(X\ni x,t_iB_i)$
, a contradiction.
To end this section, we ask the following:
Conjecture 6.6. Let
![]() ${\Gamma }\subseteq [0,1]$
be a finite set and
${\Gamma }\subseteq [0,1]$
be a finite set and
![]() $X\ni x$
a klt germ. Then there exists a positive real number
$X\ni x$
a klt germ. Then there exists a positive real number
![]() $\tau $
depending only on
$\tau $
depending only on
![]() ${\Gamma }$
and
${\Gamma }$
and
![]() $X\ni x$
satisfying the following.
$X\ni x$
satisfying the following.
Assume that:
-
(1)
 $B'\le B$
,
$B'\le B$
,
 $||B-B'||<\tau ,B\in {\Gamma }$
and
$||B-B'||<\tau ,B\in {\Gamma }$
and -
(2)
 $K_X+B'$
is
$K_X+B'$
is
 $\mathbb {R}$
-Cartier.
$\mathbb {R}$
-Cartier.
Then
![]() $K_X+B$
is
$K_X+B$
is
![]() $\mathbb {R}$
-Cartier.
$\mathbb {R}$
-Cartier.
Acknowledgements
We would like to thank Guodu Chen, Jihao Liu, Wenfei Liu, Yuchen Liu and Yusuke Nakmura for their interests and and helpful comments. We would also like to thank Paolo Cascini, Chenyang Xu and Lei Zhang for answering our questions about characteristic p. The first named author was supported by a grant from the Simons Foundation (Grant number 814268, Mathematical Sciences Research Institute (MSRI)) and Start-up Grant no. JIH1414011Y of Fudan University. We thank the referees for useful suggestions and comments.
Competing Interests
None.