Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-04T21:15:58.838Z Has data issue: false hasContentIssue false
  • English
  • Français

NONCOMMUTATIVE REAL ALGEBRAIC GEOMETRY OF KAZHDAN’S PROPERTY (T)

Part of: Special aspects of infinite or finite groups Selfadjoint operator algebras Locally compact groups and their algebras

Published online by Cambridge University Press:  30 July 2014

Narutaka Ozawa
Narutaka Ozawa*
Affiliation:
RIMS, Kyoto University, 606-8502, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that a finitely generated group ${\rm\Gamma}$ has Kazhdan’s property (T) if and only if the Laplacian element 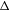${\rm\Delta}$ in 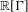$\mathbb{R}[{\rm\Gamma}]$ has a spectral gap. In this paper, we prove that this phenomenon is witnessed in 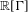$\mathbb{R}[{\rm\Gamma}]$. Namely, ${\rm\Gamma}$ has property (T) if and only if there exist a constant 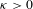${\it\kappa}>0$ and a finite sequence 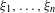${\it\xi}_{1},\ldots ,{\it\xi}_{n}$ in 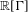$\mathbb{R}[{\rm\Gamma}]$ such that 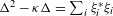${\rm\Delta}^{2}-{\it\kappa}{\rm\Delta}=\sum _{i}{\it\xi}_{i}^{\ast }{\it\xi}_{i}$. This result suggests the possibility of finding new examples of property (T) groups by solving equations in 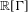$\mathbb{R}[{\rm\Gamma}]$, possibly with the assistance of computers.

Keywords

Kazhdan’s property (T)Positivstellensätzspectral gap

MSC classification

Primary: 46L89: Other “noncommutative” mathematics based on $C^*$-algebra theory 22D10: Unitary representations of locally compact groups 20F10: Word problems, other decision problems, connections with logic and automata
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 1 , January 2016 , pp. 85 - 90
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ballmann, W. and Świątkowski, J., On L 2 -cohomology and property (T) for automorphism groups of polyhedral cell complexes, Geom. Funct. Anal. 7 (1997), 615–645.Google Scholar
Barvinok, A., A course in convexity, Graduate Studies in Mathematics, Volume 54, x+366pp. (American Mathematical Society, Providence, RI, 2002).Google Scholar
Bekka, B., de la Harpe, P. and Valette, A., Kazhdan’s property (T), New Mathematical Monographs, Volume 11, xiv+472pp. (Cambridge University Press, Cambridge, 2008).Google Scholar
Brown, N. and Ozawa, N., C∗ -algebras and finite-dimensional approximations, Graduate Studies in Mathematics, Volume 88 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Netzer, T. and Thom, A., Real closed separation theorems and applications to group algebras, Pacific J. Math. 263 (2013), 435–452.Google Scholar
Ozawa, N., About the Connes embedding conjecture: algebraic approaches, Jpn. J. Math. 8 (2013), 147–183.Google Scholar
Schmüdgen, K., Noncommutative real algebraic geometry—some basic concepts and first ideas, in Emerging applications of algebraic geometry, The IMA Volumes in Mathematics and its Applications, Volume 149, pp. 325–350 (Springer, New York, 2009).CrossRefGoogle Scholar
Shalom, Y., Rigidity of commensurators and irreducible lattices, Invent. Math. 141 (2000), 1–54.Google Scholar
Silberman, L., Lectures at ‘Metric geometry, algorithms and groups’ at IHP in 2011.http://metric2011.wordpress.com/tag/lior-silbermans-lectures/.Google Scholar
Valette, A., Minimal projections, integrable representations and property (T), Arch. Math. (Basel) 43 (1984), 397–406.CrossRefGoogle Scholar
Żuk, A., Property (T) and Kazhdan constants for discrete groups, Geom. Funct. Anal. 13 (2003), 643–670.Google Scholar