No CrossRef data available.
Published online by Cambridge University Press: 02 April 2024
Clausen a prédit que le groupe des classes d’idèles de Chevalley d’un corps de nombres F apparaît comme le premier K-groupe de la catégorie des F-espaces vectoriels localement compacts. Cela s’est avéré vrai, et se généralise même aux groupes K supérieurs dans un sens approprié. Nous remplaçons F par une 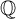 $\mathbb {Q}$-algèbre semi-simple, et obtenons le groupe des classes d’idèles noncommutatif de Fröhlich de manière analogue, modulo les éléments de norme réduite une. Même dans le cas du corps de nombres, notre preuve est plus simple que celle existante, et repose sur le théorème de localisation pour des sous-catégories percolées. Enfin, en utilisant la théorie des corps de classes, nous interprétons la loi de réciprocité d’Hilbert (ainsi qu’une variante noncommutative) en termes de nos résultats.
$\mathbb {Q}$-algèbre semi-simple, et obtenons le groupe des classes d’idèles noncommutatif de Fröhlich de manière analogue, modulo les éléments de norme réduite une. Même dans le cas du corps de nombres, notre preuve est plus simple que celle existante, et repose sur le théorème de localisation pour des sous-catégories percolées. Enfin, en utilisant la théorie des corps de classes, nous interprétons la loi de réciprocité d’Hilbert (ainsi qu’une variante noncommutative) en termes de nos résultats.
Clausen predicted that Chevalley’s idèle class group of a number field F appears as the first K-group of the category of locally compact F-vector spaces. This has turned out to be true and even generalizes to the higher K-groups in a suitable sense. We replace F by a semisimple 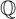 $\mathbb {Q}$-algebra and obtain Fröhlich’s noncommutative idèle class group in an analogous fashion, modulo the reduced norm one elements. Even in the number field case, our proof is simpler than the existing one and based on the localization theorem for percolating subcategories. Finally, using class field theory as input, we interpret Hilbert’s reciprocity law (as well as a noncommutative variant) in terms of our results.
$\mathbb {Q}$-algebra and obtain Fröhlich’s noncommutative idèle class group in an analogous fashion, modulo the reduced norm one elements. Even in the number field case, our proof is simpler than the existing one and based on the localization theorem for percolating subcategories. Finally, using class field theory as input, we interpret Hilbert’s reciprocity law (as well as a noncommutative variant) in terms of our results.
The first author was supported by DFG GK1821 “Cohomological Methods in Geometry”. The third author was supported by FWO (12.M33.16N)