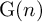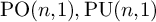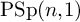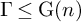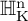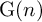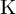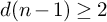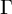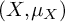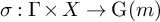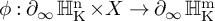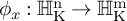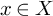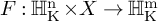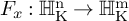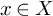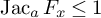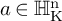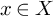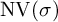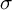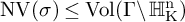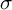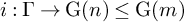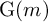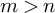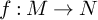1 Introduction
Let
![]() $(M,g)$
be a compact Riemannian n-manifold which admits a locally symmetric Riemannian metric
$(M,g)$
be a compact Riemannian n-manifold which admits a locally symmetric Riemannian metric
![]() $g_0$
. The minimal entropy conjecture states that the functional given by the volume entropy suitably rescaled by the volume of g – that is,
$g_0$
. The minimal entropy conjecture states that the functional given by the volume entropy suitably rescaled by the volume of g – that is,
![]() $(h_{\textrm {vol}}(g))^n\operatorname {\mathrm {\textrm {Vol}}}(M,g)$
– is minimised uniquely by the locally symmetric structure(s) on M, up to a possible homothety ([Reference Gromov32]). A positive answer for surfaces is given by Besson, Curtois and Gallot [Reference Boland and Connell5], but in this case one has to notice that there exist infinitely many inequivalent hyperbolic structures. On the contrary, when
$(h_{\textrm {vol}}(g))^n\operatorname {\mathrm {\textrm {Vol}}}(M,g)$
– is minimised uniquely by the locally symmetric structure(s) on M, up to a possible homothety ([Reference Gromov32]). A positive answer for surfaces is given by Besson, Curtois and Gallot [Reference Boland and Connell5], but in this case one has to notice that there exist infinitely many inequivalent hyperbolic structures. On the contrary, when
![]() $n \geq 3$
, there exists a unique locally symmetric structure on a compact manifold of rank 1. For those, a proof of the conjecture is given by Besson, Courtois and Gallot [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] with the introduction of the so-called natural maps, whereas in the higher rank case the conjecture is still open.
$n \geq 3$
, there exists a unique locally symmetric structure on a compact manifold of rank 1. For those, a proof of the conjecture is given by Besson, Courtois and Gallot [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] with the introduction of the so-called natural maps, whereas in the higher rank case the conjecture is still open.
Natural maps revealed a very powerful tool and, for this reason, they have been used in the study of many other different problems. For instance Boland, Connell and Souto [Reference Boland, Connell and Souto10] applied them to the study of volume rigidity of nonuniform real hyperbolic lattices. Another example was given by Francaviglia and Klaff. In [Reference Francaviglia25, Reference Fisher, Morris and Whyte24] the authors exploited the notion of natural map to study the rigidity of representations of real hyperbolic lattices. Given a torsion-free lattice
![]() $\Gamma \leq \operatorname {\mathrm {{\rm PO}}}^\circ (n,1)$
and a representation
$\Gamma \leq \operatorname {\mathrm {{\rm PO}}}^\circ (n,1)$
and a representation
![]() $\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm PO}}}(m,1)$
with
$\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm PO}}}(m,1)$
with
![]() $m \geq n \geq 3$
, they showed the existence of a smooth
$m \geq n \geq 3$
, they showed the existence of a smooth
![]() $\rho $
-equivariant map
$\rho $
-equivariant map
![]() $F: \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}}}^m_{\operatorname {\mathrm {\mathbb {R}}}}$
which satisfies
$F: \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}}}^m_{\operatorname {\mathrm {\mathbb {R}}}}$
which satisfies
![]() $\operatorname {\mathrm {\textrm {Jac}}} _a F \leq 1$
for every
$\operatorname {\mathrm {\textrm {Jac}}} _a F \leq 1$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}}$
. Additionally, when
$a \in \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}}$
. Additionally, when
![]() $\Gamma $
is nonuniform, they introduced a family of differentiable maps
$\Gamma $
is nonuniform, they introduced a family of differentiable maps
![]() $F^\varepsilon :\operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}}}^m_{\operatorname {\mathrm {\mathbb {R}}}}$
depending on
$F^\varepsilon :\operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}}}^m_{\operatorname {\mathrm {\mathbb {R}}}}$
depending on
![]() $\varepsilon>0$
, which are still
$\varepsilon>0$
, which are still
![]() $\rho $
-equivariant, properly ending and satisfy
$\rho $
-equivariant, properly ending and satisfy
![]() $\operatorname {\mathrm {\textrm {Jac}}}_a F^\varepsilon \leq (1+\varepsilon )$
for every
$\operatorname {\mathrm {\textrm {Jac}}}_a F^\varepsilon \leq (1+\varepsilon )$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}}$
(the properly ending property can be interpreted as a compatibility condition of the map on the peripheral subgroups of
$a \in \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}}$
(the properly ending property can be interpreted as a compatibility condition of the map on the peripheral subgroups of
![]() $\Gamma $
). The constructions described above allow the introduction of the notion of volume
$\Gamma $
). The constructions described above allow the introduction of the notion of volume
![]() $\operatorname {\mathrm {\textrm {Vol}}}(\rho )$
of the representation
$\operatorname {\mathrm {\textrm {Vol}}}(\rho )$
of the representation
![]() $\rho $
by considering the infimum over all possible volumes
$\rho $
by considering the infimum over all possible volumes
![]() $\operatorname {\mathrm {\textrm {Vol}}}(D)$
, where D is a smooth
$\operatorname {\mathrm {\textrm {Vol}}}(D)$
, where D is a smooth
![]() $\rho $
-equivariant map (which properly ends in the nonunifom case).
$\rho $
-equivariant map (which properly ends in the nonunifom case).
Volume of representations remains unchanged under the conjugation by an element
![]() $g \in \operatorname {\mathrm {{\rm PO}}}(m,1)$
and it satisfies a Milnor–Wood type inequality. Indeed, we have that
$g \in \operatorname {\mathrm {{\rm PO}}}(m,1)$
and it satisfies a Milnor–Wood type inequality. Indeed, we have that
![]() $\operatorname {\mathrm {\textrm {Vol}}}(\rho ) \leq \operatorname {\mathrm {\textrm {Vol}}}(\Gamma \backslash \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}})$
and the equality is attained if and only if the representation is conjugated by an element of
$\operatorname {\mathrm {\textrm {Vol}}}(\rho ) \leq \operatorname {\mathrm {\textrm {Vol}}}(\Gamma \backslash \operatorname {\mathrm {\mathbb {H}}}^n_{\operatorname {\mathrm {\mathbb {R}}}})$
and the equality is attained if and only if the representation is conjugated by an element of
![]() $\operatorname {\mathrm {{\rm PO}}}(m,1)$
to the standard lattice embedding
$\operatorname {\mathrm {{\rm PO}}}(m,1)$
to the standard lattice embedding
![]() $i:\Gamma \rightarrow \operatorname {\mathrm {{\rm PO}}}(n,1) \leq \operatorname {\mathrm {{\rm PO}}}(m,1)$
, modulo possibly a compact subgroup when
$i:\Gamma \rightarrow \operatorname {\mathrm {{\rm PO}}}(n,1) \leq \operatorname {\mathrm {{\rm PO}}}(m,1)$
, modulo possibly a compact subgroup when
![]() $m> n$
. Here
$m> n$
. Here
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1)$
is realised as a subgroup of
$\operatorname {\mathrm {{\rm PO}}}(n,1)$
is realised as a subgroup of
![]() $\operatorname {\mathrm {{\rm PO}}}(m,1)$
via the upper-left corner embedding.
$\operatorname {\mathrm {{\rm PO}}}(m,1)$
via the upper-left corner embedding.
Notice that when
![]() $n=m=3$
the volume of a representation coincides with the definition given independently by Dunfield [Reference Dunfield20] and by Francaviglia [Reference Frigerio and Moraschini23] in terms of pseudo-developing maps (both definitions generalise the notion of volume of a hyperbolic structure reported, for instance, in [Reference Nicholls40]). It is worth mentioning that similar rigidity results have been obtained by Bucher, Burger and Iozzi [Reference Burger and Iozzi12] in the case
$n=m=3$
the volume of a representation coincides with the definition given independently by Dunfield [Reference Dunfield20] and by Francaviglia [Reference Frigerio and Moraschini23] in terms of pseudo-developing maps (both definitions generalise the notion of volume of a hyperbolic structure reported, for instance, in [Reference Nicholls40]). It is worth mentioning that similar rigidity results have been obtained by Bucher, Burger and Iozzi [Reference Burger and Iozzi12] in the case
![]() $n=m$
. However, their approach to the problem is completely different and their definition of volume of representations relies on the study of the bounded cohomology groups of
$n=m$
. However, their approach to the problem is completely different and their definition of volume of representations relies on the study of the bounded cohomology groups of
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1)$
.
$\operatorname {\mathrm {{\rm PO}}}(n,1)$
.
In the context of rank-1 torsion-free lattices, similar questions have been studied for complex and quaternionic lattices. Given a nonuniform torsion-free lattice
![]() $\Gamma \leq \operatorname {\mathrm {{\rm PU}}}(n,1)$
and a representation
$\Gamma \leq \operatorname {\mathrm {{\rm PU}}}(n,1)$
and a representation
![]() $\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm PU}}}(m,1)$
with
$\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm PU}}}(m,1)$
with
![]() $m \geq n \geq 2$
, Koziarz and Maubon [Reference Kneser34] proved a rigidity result analogous to the one described above but using the theory of harmonic maps. In [Reference Burger and Mozes13] Burger and Iozzi obtained the same statement for both uniform and nonuniform lattices using jointly bounded cohomology and
$m \geq n \geq 2$
, Koziarz and Maubon [Reference Kneser34] proved a rigidity result analogous to the one described above but using the theory of harmonic maps. In [Reference Burger and Mozes13] Burger and Iozzi obtained the same statement for both uniform and nonuniform lattices using jointly bounded cohomology and
![]() $\operatorname {\mathrm {\textrm {L}}}^2$
-cohomology. Regarding the study of quaternionic lattices, it is worth mentioning the superrigidity result that Corlette obtained in [Reference Corlette17].
$\operatorname {\mathrm {\textrm {L}}}^2$
-cohomology. Regarding the study of quaternionic lattices, it is worth mentioning the superrigidity result that Corlette obtained in [Reference Corlette17].
Recently the author has shown in [Reference Francaviglia26, Reference Savini44] a stronger rigidity phenomenon for the volume function. Indeed, volume of representations of any rank-1 torsion-free nonuniform lattice is rigid at the ideal points of the character variety. For instance, if
![]() $\Gamma $
is a torsion-free nonuniform real hyperbolic lattice, the character variety
$\Gamma $
is a torsion-free nonuniform real hyperbolic lattice, the character variety
![]() $X(\Gamma ,\operatorname {\mathrm {{\rm PO}}}(m,1))$
is an algebraic set of positive dimension and a divergent sequence of representations cannot eventually maximise the volume. The same result can be suitably adapted to the context of complex and quaternionic lattices. To sum up, one could say that for rank-1 torsion-free lattices the volume of representations is asymptotically rigid.
$X(\Gamma ,\operatorname {\mathrm {{\rm PO}}}(m,1))$
is an algebraic set of positive dimension and a divergent sequence of representations cannot eventually maximise the volume. The same result can be suitably adapted to the context of complex and quaternionic lattices. To sum up, one could say that for rank-1 torsion-free lattices the volume of representations is asymptotically rigid.
As already noted, the minimal entropy conjecture is still open in the higher rank case. However, it is worth mentioning some efforts which move towards the direction of a proof. In [Reference Connell and Farb16] Connell and Farb succeeded in extending the construction of natural maps to lattices in products of rank-1 Lie groups of noncompact type. The key point is that they proved an estimate on the Jacobian of the natural map which is still sharp. Similarly, they obtained a uniform, but not sharp, Jacobian estimate for more general higher rank symmetric spaces ([Reference Connell and Farb15]).
Other interesting applications of natural maps have been found for foliations of Riemannian manifolds with locally symmetric negatively curved leaves ([Reference Besson, Courtois and Gallot9]) and for Finsler/Benoist manifolds ([Reference Bader, Furman and Sauer11, Reference Adeboye, Bray and Constantine1, Reference Savini46]).
In this article, we want to extend the notion of natural map to the setting of Zimmer’s cocycles theory in order to study rigidity phenomena. Recently this kind of study has been developed by the author and Moraschini using the theory of bounded cohomology (see, for instance, [Reference Savini47, Reference Savini45, Reference Moraschini and Savini36, Reference Moraschini and Savini37]). Here we want to give a differentiable approach to this subject. More precisely, denote by
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
either
$\operatorname {\mathrm {{\rm G}}}(n)$
either
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
$\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
![]() $\operatorname {\mathrm {\textrm {PSp}}}(n,1)$
and let
$\operatorname {\mathrm {\textrm {PSp}}}(n,1)$
and let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice. Since it is well-known that the Riemannian symmetric space associated to
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice. Since it is well-known that the Riemannian symmetric space associated to
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
is a hyperbolic space on a suitable division algebra
$\operatorname {\mathrm {{\rm G}}}(n)$
is a hyperbolic space on a suitable division algebra
![]() $\operatorname {\mathrm {{\rm K}}}$
, we denote it by
$\operatorname {\mathrm {{\rm K}}}$
, we denote it by
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. If we denote by
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. If we denote by
![]() $d=\textrm {dim}_{\operatorname {\mathrm {\mathbb {R}}}} \operatorname {\mathrm {{\rm K}}}$
the real dimension of the division algebra
$d=\textrm {dim}_{\operatorname {\mathrm {\mathbb {R}}}} \operatorname {\mathrm {{\rm K}}}$
the real dimension of the division algebra
![]() $\operatorname {\mathrm {{\rm K}}}$
, we will need to assume
$\operatorname {\mathrm {{\rm K}}}$
, we will need to assume
![]() $d(n-1) \geq 2$
. Fix now a standard Borel probability
$d(n-1) \geq 2$
. Fix now a standard Borel probability
![]() $\Gamma $
-space
$\Gamma $
-space
![]() $(X,\mu _X)$
without atoms. Suppose
$(X,\mu _X)$
without atoms. Suppose
![]() $m \geq n$
and consider a Zimmer’s cocycle
$m \geq n$
and consider a Zimmer’s cocycle
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
with an essentially unique
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
with an essentially unique
![]() $\sigma $
-equivariant measurable map
$\sigma $
-equivariant measurable map
![]() $\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. The boundary map
$\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. The boundary map
![]() $\phi $
allows us to define for almost every
$\phi $
allows us to define for almost every
![]() $x \in X$
the slice
$x \in X$
the slice
![]() $\phi _x:\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
given by
$\phi _x:\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
given by
![]() $\phi _x(\xi ):=\phi (\xi ,x)$
. Notice that for almost every
$\phi _x(\xi ):=\phi (\xi ,x)$
. Notice that for almost every
![]() $x \in X$
the slice
$x \in X$
the slice
![]() $\phi _x$
is measurable since X is standard Borel ([Reference Feldman and Moore22, Lemma 2.6]). Supposing that for almost every slice
$\phi _x$
is measurable since X is standard Borel ([Reference Feldman and Moore22, Lemma 2.6]). Supposing that for almost every slice
![]() $\phi _x$
the push-forward of the Patterson–Sullivan measure is atom-free (hence the slice is atomless), we can apply the barycenter construction to get the desired natural map. In this way we obtain the following.
$\phi _x$
the push-forward of the Patterson–Sullivan measure is atom-free (hence the slice is atomless), we can apply the barycenter construction to get the desired natural map. In this way we obtain the following.
Theorem 1.1. Let
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
be either
$\operatorname {\mathrm {{\rm G}}}(n)$
be either
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
$\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
![]() $\operatorname {\mathrm {\textrm {PSp}}}(n,1)$
and denote by
$\operatorname {\mathrm {\textrm {PSp}}}(n,1)$
and denote by
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the associated hyperbolic space over the division algebra
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the associated hyperbolic space over the division algebra
![]() $\operatorname {\mathrm {{\rm K}}}$
of dimension
$\operatorname {\mathrm {{\rm K}}}$
of dimension
![]() $d=\dim _{\operatorname {\mathrm {\mathbb {R}}}} \operatorname {\mathrm {{\rm K}}}$
. Let
$d=\dim _{\operatorname {\mathrm {\mathbb {R}}}} \operatorname {\mathrm {{\rm K}}}$
. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
![]() $(X,\mu _X)$
a standard Borel probability
$(X,\mu _X)$
a standard Borel probability
![]() $\Gamma $
-space. Suppose
$\Gamma $
-space. Suppose
![]() $d(n-1) \geq 2$
and take
$d(n-1) \geq 2$
and take
![]() $m \geq n$
. Given a measurable cocycle
$m \geq n$
. Given a measurable cocycle
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, assume there exists an essentially unique boundary map
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, assume there exists an essentially unique boundary map
![]() $\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with atomless slices. Then there exists a measurable map
$\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with atomless slices. Then there exists a measurable map
![]() $F: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
which is
$F: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
which is
![]() $\sigma $
-equivariant. Additionally, for almost every
$\sigma $
-equivariant. Additionally, for almost every
![]() $x \in X$
the slice
$x \in X$
the slice
![]() $F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is smooth and we have
$F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is smooth and we have
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The equality is attained if and only if the map
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The equality is attained if and only if the map
![]() $D_aF_x: T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow T_{F_x(a)} \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is an isometric embedding.
$D_aF_x: T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow T_{F_x(a)} \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is an isometric embedding.
Since the map
![]() $F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is a clear generalisation of the natural map defined by Besson, Courtois and Gallot to the context of Zimmer’s cocycles, we are going to say that F is the natural map associated to the cocycle
$F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is a clear generalisation of the natural map defined by Besson, Courtois and Gallot to the context of Zimmer’s cocycles, we are going to say that F is the natural map associated to the cocycle
![]() $\sigma $
. Even if the condition on the slices of the boundary map may seem quite restrictive, natural maps exist for measurable cocycles coming from couplings, as shown by Bader, Furman and Sauer [Reference Bucher, Burger and Iozzi4, Lemma 3.6] and by the author [Reference Savini48, Lemma 3.1].
$\sigma $
. Even if the condition on the slices of the boundary map may seem quite restrictive, natural maps exist for measurable cocycles coming from couplings, as shown by Bader, Furman and Sauer [Reference Bucher, Burger and Iozzi4, Lemma 3.6] and by the author [Reference Savini48, Lemma 3.1].
We are also going to define the notion of volume associated to
![]() $\sigma $
. Our definition will differ from the one given by Francaviglia and Klaff for representations. Indeed, here we are going to concentrate our attention only to the natural map associated to a fixed cocycle, without taking any infimum over all possible volumes of equivariant maps.
$\sigma $
. Our definition will differ from the one given by Francaviglia and Klaff for representations. Indeed, here we are going to concentrate our attention only to the natural map associated to a fixed cocycle, without taking any infimum over all possible volumes of equivariant maps.
Given any
![]() $\sigma $
-equivariant measurable map
$\sigma $
-equivariant measurable map
![]() $\Phi : \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with differentiable slice
$\Phi : \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with differentiable slice
![]() $\Phi _x: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
for almost every
$\Phi _x: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
for almost every
![]() $x \in X$
, we can consider the volume form associated to the pullback metric
$x \in X$
, we can consider the volume form associated to the pullback metric
![]() $(\omega _x)_a(u_1,\ldots ,u_p):=\sqrt { \det g_m(D_a\Phi _x(u_i),D_a\Phi _x(u_j))}$
, where
$(\omega _x)_a(u_1,\ldots ,u_p):=\sqrt { \det g_m(D_a\Phi _x(u_i),D_a\Phi _x(u_j))}$
, where
![]() $u_1,\ldots ,u_p \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
$u_1,\ldots ,u_p \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
![]() $g_m$
is the standard Riemannian metric on
$g_m$
is the standard Riemannian metric on
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. When
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. When
![]() $\Phi $
satisfies the essential boundedness condition, we obtain a measurable family of differential forms
$\Phi $
satisfies the essential boundedness condition, we obtain a measurable family of differential forms
![]() $\{ \omega _x \}_{x \in X}$
on
$\{ \omega _x \}_{x \in X}$
on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(see Section 4). Hence, by considering its integral over X, we obtain a differential form on
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(see Section 4). Hence, by considering its integral over X, we obtain a differential form on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which is
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which is
![]() $\Gamma $
-invariant by the equivariance of the map
$\Gamma $
-invariant by the equivariance of the map
![]() $\Phi $
. Thus, we have a differential form on
$\Phi $
. Thus, we have a differential form on
![]() $\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and we can take its integral. This number will be the volume associated to the measurable map
$\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and we can take its integral. This number will be the volume associated to the measurable map
![]() $\Phi $
. If we specialise to the case of the natural map, which is essentially bounded, we call it the natural volume
$\Phi $
. If we specialise to the case of the natural map, which is essentially bounded, we call it the natural volume
![]() $\operatorname {\mathrm {\textrm {NV}}}(\sigma )$
of
$\operatorname {\mathrm {\textrm {NV}}}(\sigma )$
of
![]() $\sigma $
.
$\sigma $
.
Clearly, the natural volume of a cocycle will be invariant by the conjugation action of
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
on the space of cocycles. Moreover, this volume satisfies a Milnor–Wood inequality type similar to the one obtained by Bucher, Burger and Iozzi [Reference Burger and Iozzi12] for representations, by Bader, Furman and Sauer [Reference Bucher, Burger and Iozzi4] for self-couplings and by the author and Moraschini [Reference Moraschini and Savini36, Reference Moraschini and Savini37] for cocycles. Notice that the result obtained in [Reference Moraschini and Savini36] is valid for
$\operatorname {\mathrm {{\rm G}}}(m)$
on the space of cocycles. Moreover, this volume satisfies a Milnor–Wood inequality type similar to the one obtained by Bucher, Burger and Iozzi [Reference Burger and Iozzi12] for representations, by Bader, Furman and Sauer [Reference Bucher, Burger and Iozzi4] for self-couplings and by the author and Moraschini [Reference Moraschini and Savini36, Reference Moraschini and Savini37] for cocycles. Notice that the result obtained in [Reference Moraschini and Savini36] is valid for
![]() $n=m$
, whereas here we can also consider the case
$n=m$
, whereas here we can also consider the case
![]() $m>n$
.
$m>n$
.
The Milnor–Wood inequality obtained here will be crucial to prove the following rigidity result.
Theorem 1.2. Let
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
be either
$\operatorname {\mathrm {{\rm G}}}(n)$
be either
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
$\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
![]() $\operatorname {\mathrm {{\rm PSp}}}(n,1)$
and denote by
$\operatorname {\mathrm {{\rm PSp}}}(n,1)$
and denote by
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the associated hyperbolic space over the division algebra
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the associated hyperbolic space over the division algebra
![]() $\operatorname {\mathrm {{\rm K}}}$
of dimension
$\operatorname {\mathrm {{\rm K}}}$
of dimension
![]() $d=\dim _{\operatorname {\mathrm {\mathbb {R}}}} \operatorname {\mathrm {{\rm K}}}$
. Let
$d=\dim _{\operatorname {\mathrm {\mathbb {R}}}} \operatorname {\mathrm {{\rm K}}}$
. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
![]() $(X,\mu _X)$
a standard Borel probability
$(X,\mu _X)$
a standard Borel probability
![]() $\Gamma $
-space. Suppose
$\Gamma $
-space. Suppose
![]() $d(n-1) \geq 2$
and take
$d(n-1) \geq 2$
and take
![]() $m \geq n$
. Given a measurable cocycle
$m \geq n$
. Given a measurable cocycle
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, assume there exists an essentially unique boundary map
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, assume there exists an essentially unique boundary map
![]() $\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with atomless slices. Then
$\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with atomless slices. Then
and the equality holds if and only if
![]() $\sigma $
is cohomologous to the cocycle induced by the standard lattice embedding
$\sigma $
is cohomologous to the cocycle induced by the standard lattice embedding
![]() $i:\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(n) \leq \operatorname {\mathrm {{\rm G}}}(m)$
, modulo possibly a compact subgroup of
$i:\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(n) \leq \operatorname {\mathrm {{\rm G}}}(m)$
, modulo possibly a compact subgroup of
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
when
$\operatorname {\mathrm {{\rm G}}}(m)$
when
![]() $m>n$
. Here
$m>n$
. Here
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
is realised into
$\operatorname {\mathrm {{\rm G}}}(n)$
is realised into
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
via the upper-left corner embedding.
$\operatorname {\mathrm {{\rm G}}}(m)$
via the upper-left corner embedding.
First notice that for both Theorem 1.1 and Theorem 1.2 the hypothesis of uniformity of the lattice
![]() $\Gamma $
is not crucial. Hence, the same results can also be generalised to nonuniform lattices. A suitable variation of Theorem 1.2 has been exploited by the author [Reference Savini48] to show that the group
$\Gamma $
is not crucial. Hence, the same results can also be generalised to nonuniform lattices. A suitable variation of Theorem 1.2 has been exploited by the author [Reference Savini48] to show that the group
![]() $\operatorname {\mathrm {{\rm PU}}}(n,1)$
is
$\operatorname {\mathrm {{\rm PU}}}(n,1)$
is
![]() $1$
-taut in the sense of Bader, Furman and Sauer [Reference Bucher, Burger and Iozzi4]. That problem was an open conjecture whose proof allows us to classify finitely generated groups that are integrable measure equivalent to a complex hyperbolic lattice.
$1$
-taut in the sense of Bader, Furman and Sauer [Reference Bucher, Burger and Iozzi4]. That problem was an open conjecture whose proof allows us to classify finitely generated groups that are integrable measure equivalent to a complex hyperbolic lattice.
The proof of Theorem 1.2 relies on the sharpness on the estimate of the Jacobian of the slices of F. More precisely, one can see that if the volume of
![]() $\sigma $
is maximal, then for almost every
$\sigma $
is maximal, then for almost every
![]() $x \in X$
the Jacobian must satisfy
$x \in X$
the Jacobian must satisfy
![]() $\operatorname {\mathrm {\textrm {Jac}}}_a F_x=1$
for almost every
$\operatorname {\mathrm {\textrm {Jac}}}_a F_x=1$
for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. In particular, the slice
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. In particular, the slice
![]() $F_x$
coincides essentially with a totally geodesic embedding and hence it is essentially equal to an element
$F_x$
coincides essentially with a totally geodesic embedding and hence it is essentially equal to an element
![]() $F_x=f(x) \in \operatorname {\mathrm {{\rm G}}}(m)$
. In this way, we obtain a map
$F_x=f(x) \in \operatorname {\mathrm {{\rm G}}}(m)$
. In this way, we obtain a map
![]() $f: X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
whose measurability is guaranteed by [Reference Feldman and Moore22, Lemma 2.6]. We conclude the proof applying the strategy exposed in [Reference Bucher, Burger and Iozzi4, Proposition 3.2] and adding a measurable function into a compact subgroup of
$f: X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
whose measurability is guaranteed by [Reference Feldman and Moore22, Lemma 2.6]. We conclude the proof applying the strategy exposed in [Reference Bucher, Burger and Iozzi4, Proposition 3.2] and adding a measurable function into a compact subgroup of
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
, when
$\operatorname {\mathrm {{\rm G}}}(m)$
, when
![]() $m>n$
.
$m>n$
.
The notion of volume is also useful to study the mapping degree of continuous maps between closed hyperbolic manifolds of the same dimension. The mapping degree theorem, first stated by Kneser [Reference Koziarz and Maubon33] for surfaces and then extended by Thurston [Reference Thurston50] in the higher dimensional case, states that given a continuous map
![]() $f:M \rightarrow N$
between closed real hyperbolic manifolds of the same dimension, it must hold that
$f:M \rightarrow N$
between closed real hyperbolic manifolds of the same dimension, it must hold that
 $$ \begin{align*}|\deg(f)| \leq \frac{\operatorname{\mathrm{{\rm Vol}}}(M)}{\operatorname{\mathrm{{\rm Vol}}}(N)} . \\[-16pt]\end{align*} $$
$$ \begin{align*}|\deg(f)| \leq \frac{\operatorname{\mathrm{{\rm Vol}}}(M)}{\operatorname{\mathrm{{\rm Vol}}}(N)} . \\[-16pt]\end{align*} $$
Additionally, the strict version [Reference Thurston50, Theorem 6.4] of the theorem characterises local isometries as those maps satisfying the equality.
Several proofs of the mapping degree theorem have been given so far. For instance, Thurston [Reference Thurston50] and Gromov [Reference Gromov31] used
![]() $\ell ^1$
-homology and the notion of simplicial volume. Besson, Courtois and Gallot [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] obtained a proof based on their concept of natural map (generalised later by Connell and Farb [Reference Connell and Farb16, Reference Connell and Farb15] to the higher rank case). For real hyperbolic manifolds, it is worth mentioning the approach of Bucher, Burger and Iozzi [Reference Burger and Iozzi12] based on the study of bounded cohomology groups of
$\ell ^1$
-homology and the notion of simplicial volume. Besson, Courtois and Gallot [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] obtained a proof based on their concept of natural map (generalised later by Connell and Farb [Reference Connell and Farb16, Reference Connell and Farb15] to the higher rank case). For real hyperbolic manifolds, it is worth mentioning the approach of Bucher, Burger and Iozzi [Reference Burger and Iozzi12] based on the study of bounded cohomology groups of
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1)$
. Similarly, the author and Moraschini [Reference Moraschini and Savini36] obtained an analogous proof by studying the notion of maximal Zimmer cocycles.
$\operatorname {\mathrm {{\rm PO}}}(n,1)$
. Similarly, the author and Moraschini [Reference Moraschini and Savini36] obtained an analogous proof by studying the notion of maximal Zimmer cocycles.
The interest in the relation between the mapping degree of continuous maps and the volume of manifolds led to a rich and fruitful literature [Reference Löh and Kotschick35, Reference Neofitydis38, Reference Neofitydis39, Reference Francaviglia and Savini27]. Derbez et al. [Reference Douady and Earle18, Proposition 3.1] were able to express the volume of the pullback of a representation
![]() $\rho $
along a continuous map f as the product of the mapping degree of f with the volume of
$\rho $
along a continuous map f as the product of the mapping degree of f with the volume of
![]() $\rho $
. The same has been done in [Reference Moraschini and Savini36] in the case of maximal cocycles. Here we want to generalise this result to the context of measurable maps with smooth slices which are equivariant with respect to a fixed measurable cocycle. Given a continuous map
$\rho $
. The same has been done in [Reference Moraschini and Savini36] in the case of maximal cocycles. Here we want to generalise this result to the context of measurable maps with smooth slices which are equivariant with respect to a fixed measurable cocycle. Given a continuous map
![]() $f:M \rightarrow N$
and a measurable equivariant map
$f:M \rightarrow N$
and a measurable equivariant map
![]() $\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
, one can suitably define the notion of pullback map
$\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
, one can suitably define the notion of pullback map
![]() $f^\ast \Phi $
along the continuous map f (see Section 5). Then we have the following version of the mapping degree theorem.
$f^\ast \Phi $
along the continuous map f (see Section 5). Then we have the following version of the mapping degree theorem.
Proposition 1.3. Let
![]() $\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Set
$\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Set
![]() $M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
,
$M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
,
![]() $N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and let
$N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and let
![]() $f:M \rightarrow N$
be a continuous map with nonvanishing degree. Fix a standard Borel probability
$f:M \rightarrow N$
be a continuous map with nonvanishing degree. Fix a standard Borel probability
![]() $\Lambda $
-space
$\Lambda $
-space
![]() $(X,\mu _X)$
and consider a measurable cocycle
$(X,\mu _X)$
and consider a measurable cocycle
![]() $\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
. Given any measurable
$\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
. Given any measurable
![]() $\sigma $
-equivariant map
$\sigma $
-equivariant map
![]() $\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with essentially bounded smooth slices, we have that
$\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
with essentially bounded smooth slices, we have that
 $$ \begin{align*}|\deg(f)| \leq \frac{\operatorname{\mathrm{{\rm Vol}}}(f^\ast \Phi)}{\operatorname{\mathrm{{\rm Vol}}}(\Phi)} . \\[-16pt]\end{align*} $$
$$ \begin{align*}|\deg(f)| \leq \frac{\operatorname{\mathrm{{\rm Vol}}}(f^\ast \Phi)}{\operatorname{\mathrm{{\rm Vol}}}(\Phi)} . \\[-16pt]\end{align*} $$
Additionally, if f is homotopic to a local isometry, then the equality is attained.
The proof of the latter statement will rely essentially on both the co-area formula and on Thurston’s strict version of mapping degree theorem. If in the previous proposition we consider the particular case when
![]() $\Phi $
is the natural map associated to
$\Phi $
is the natural map associated to
![]() $\sigma $
, then we get an inequality which relates the volume of
$\sigma $
, then we get an inequality which relates the volume of
![]() $f^\ast \Phi $
and the natural volume of
$f^\ast \Phi $
and the natural volume of
![]() $\sigma $
; that is,
$\sigma $
; that is,
 $$ \begin{align*}|\deg(f)| \leq \frac{ \operatorname{\mathrm{{\rm Vol}}}(f^\ast \Phi)}{\operatorname{\mathrm{{\rm NV}}}(\sigma)} . \end{align*} $$
$$ \begin{align*}|\deg(f)| \leq \frac{ \operatorname{\mathrm{{\rm Vol}}}(f^\ast \Phi)}{\operatorname{\mathrm{{\rm NV}}}(\sigma)} . \end{align*} $$
It is worth noticing that a priori we do not know if
![]() $f^\ast \Phi $
is the natural map associated to
$f^\ast \Phi $
is the natural map associated to
![]() $f^\ast \sigma $
, so we cannot push any further our reasoning. Nevertheless, the above estimate allows us to characterise maps homotopic to local isometries in terms of naturally maximal cocycles; that is, cocycles with maximal natural volume (compare with [Reference Moraschini and Savini36, Proposition 1.3]).
$f^\ast \sigma $
, so we cannot push any further our reasoning. Nevertheless, the above estimate allows us to characterise maps homotopic to local isometries in terms of naturally maximal cocycles; that is, cocycles with maximal natural volume (compare with [Reference Moraschini and Savini36, Proposition 1.3]).
Plan of the article
Section 2 is devoted to recall the main definitions and results that we will need in the article. More precisely, in Subsection 2.1 we briefly recall Zimmer’s cocycles theory. We move then to the definition of barycenter for atom-free probability measures on the boundary at infinity
![]() $\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, described in Subsection 2.2. Then in Subsection 2.3 we expose the notion of the Patterson–Sullivan density associated to a lattice and the construction of the Besson–Courtois–Gallot natural map. The crucial definition of natural map associated to a Zimmer cocycle appears in Section 3, where we also discuss all of its properties. We show that it can be suitably interpreted as a generalisation of the natural map for representations (Proposition 3.3). Additionally, we show how natural maps vary along the
$\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, described in Subsection 2.2. Then in Subsection 2.3 we expose the notion of the Patterson–Sullivan density associated to a lattice and the construction of the Besson–Courtois–Gallot natural map. The crucial definition of natural map associated to a Zimmer cocycle appears in Section 3, where we also discuss all of its properties. We show that it can be suitably interpreted as a generalisation of the natural map for representations (Proposition 3.3). Additionally, we show how natural maps vary along the
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class (Proposition 3.4).
$\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class (Proposition 3.4).
We move to Section 4. Here we introduce the notion of volume of a measurable equivariant map with essentially bounded differentiable slices and subsequently the notion of natural volume of measurable cocycles (see Definitions 4.1 and 4.3). Then the main rigidity result is proved.
We conclude with Section 5, where we prove our version of mapping degree theorem; some comments about natural volume and naturally maximal cocycles follow.
2 Preliminary definitions and results
In this section we are going to recall briefly all of the notions we will need in the article in order to define the natural map associated to a Zimmer cocycle. For this reason, we first discuss the notion of measurable cocycle and we will see how representation theory fits into this wider context. Then we focus our attention on some elements of boundary theory, in particular on the notion of generalised boundary map. We conclude this digression by talking about the Patterson–Sullivan measures and the barycenter construction. We will need both to construct our natural map. Indeed, we are going to apply the barycenter to the push-foward of the Patterson–Sullivan measures with respect to the slices of the boundary map associated to a measurable cocycle.
2.1 Zimmer’s cocycle theory
For the material in the following section we mainly refer to the work of both Furstenberg [Reference Furstenberg29, Reference Furstenberg30] and Zimmer [Reference Zimmer52].
Let
![]() $G,H$
be two locally compact second countable groups endowed both with their natural Haar measure. Consider a standard Borel measure space
$G,H$
be two locally compact second countable groups endowed both with their natural Haar measure. Consider a standard Borel measure space
![]() $(X,\mu )$
on which G acts via measure-preserving transformations. We are going to call the space
$(X,\mu )$
on which G acts via measure-preserving transformations. We are going to call the space
![]() $(X,\mu )$
satisfying the hypothesis above a standard Borel measure G-space. If additionally
$(X,\mu )$
satisfying the hypothesis above a standard Borel measure G-space. If additionally
![]() $(X,\mu )$
is a probability space without atoms, we are going to say that
$(X,\mu )$
is a probability space without atoms, we are going to say that
![]() $(X,\mu )$
is a standard Borel probability G-space.
$(X,\mu )$
is a standard Borel probability G-space.
Given another measure space
![]() $(Y,\nu )$
, we are going to denote by
$(Y,\nu )$
, we are going to denote by
![]() $\textrm {Meas}(X,Y)$
the space of measurable functions from X to Y, endowed with the topology of the convergence in measure.
$\textrm {Meas}(X,Y)$
the space of measurable functions from X to Y, endowed with the topology of the convergence in measure.
Definition 2.1. Let
![]() $\sigma :G \times X \rightarrow H$
be a measurable function. We call
$\sigma :G \times X \rightarrow H$
be a measurable function. We call
![]() $\sigma $
a measurable cocycle (or Zimmer cocycle or simply cocycle) if the associated map
$\sigma $
a measurable cocycle (or Zimmer cocycle or simply cocycle) if the associated map
is continuous and it holds that
for every
![]() $g_1,g_2 \in G$
and almost every
$g_1,g_2 \in G$
and almost every
![]() $x \in X$
.
$x \in X$
.
In the previous definition we preferred to stress the action of G on X using the dot, but from now on we will omit this symbol.
At first sight the notion of measurable cocycle might seem quite mysterious to the reader who is not familiar with this theory. One could interpret Equation (1) either as a suitable generalisation of the chain rule for derivatives or as the classic Eilenberg–MacLane condition for Borel
![]() $1$
-cocycle (see [Reference Francaviglia and Klaff21, Reference Zimmer53]). The latter interpretation comes from viewing the cocycle as an element
$1$
-cocycle (see [Reference Francaviglia and Klaff21, Reference Zimmer53]). The latter interpretation comes from viewing the cocycle as an element
![]() $\sigma \in \textrm {Meas}(G,\textrm {Meas}(X,H))$
. Following the line of this interpretation, it is natural to also define the notion of cohomologous cocycles.
$\sigma \in \textrm {Meas}(G,\textrm {Meas}(X,H))$
. Following the line of this interpretation, it is natural to also define the notion of cohomologous cocycles.
Definition 2.2. Let
![]() $\sigma _1,\sigma _2:G \times X \rightarrow H$
be two measurable cocycles and let
$\sigma _1,\sigma _2:G \times X \rightarrow H$
be two measurable cocycles and let
![]() $f:X \rightarrow H$
be a measurable function. Then the cocycle defined by
$f:X \rightarrow H$
be a measurable function. Then the cocycle defined by
is the twisted cocycle associated to
![]() $\sigma $
and f. The two cocycles
$\sigma $
and f. The two cocycles
![]() $\sigma _1$
and
$\sigma _1$
and
![]() $\sigma _2$
are cohomologous (or equivalent) if
$\sigma _2$
are cohomologous (or equivalent) if
for some measurable function
![]() $f:X \rightarrow H$
.
$f:X \rightarrow H$
.
Measurable cocycles are quite ubiquitous in mathematics. Indeed, one can find them in several different contexts, such as differential geometry (the differentiation cocycle; see [Reference Zimmer52, Example 4.2.2]) or measure theory (the Radon–Nikodym cocycle; see [Reference Zimmer52, Example 4.2.3]). In our case, we are going to focus on a large family of cocycles coming from representation theory.
Definition 2.3. Let
![]() $\rho :G \rightarrow H$
be a continuous representation and let
$\rho :G \rightarrow H$
be a continuous representation and let
![]() $(X,\mu )$
be any standard Borel measure G-space. We define the cocycle associated to the representation
$(X,\mu )$
be any standard Borel measure G-space. We define the cocycle associated to the representation
![]() $\rho $
as follows:
$\rho $
as follows:
for every
![]() $g \in G$
and almost every
$g \in G$
and almost every
![]() $x \in X$
.
$x \in X$
.
From the definition it should be clear that any continuous representation naturally determines a measurable cocycle once we have fixed a suitable standard Borel measure G-space. Notice that even if the variable
![]() $x \in X$
does not arise in the definition above, the cocycle
$x \in X$
does not arise in the definition above, the cocycle
![]() $\sigma _\rho $
actually depends on both the representation
$\sigma _\rho $
actually depends on both the representation
![]() $\rho $
and the space X. Nevertheless, we prefer to omit the latter dependence to avoid a heavy notation. Notice also that when G is a discrete group, any representation is continuous and hence we can always define an associated measurable cocycle.
$\rho $
and the space X. Nevertheless, we prefer to omit the latter dependence to avoid a heavy notation. Notice also that when G is a discrete group, any representation is continuous and hence we can always define an associated measurable cocycle.
Another key tool we will need later is the concept of boundary map associated to a measurable cocycle. Here we are going to introduce directly the notion of generalised boundary map, even if we will not need it in its full generality. Assume first that G admits a Furstenberg–Poisson boundary
![]() $B(G)$
(see [Reference Furstenberg28] for a precise definition). A well-known example of this situation is when G is a center-free semisimple Lie group without compact factors. In this case the Furstenberg–Poisson boundary
$B(G)$
(see [Reference Furstenberg28] for a precise definition). A well-known example of this situation is when G is a center-free semisimple Lie group without compact factors. In this case the Furstenberg–Poisson boundary
![]() $B(G)$
can be identified with the homogeneous space
$B(G)$
can be identified with the homogeneous space
![]() $G/P$
, where
$G/P$
, where
![]() $P \leq G$
is any minimal parabolic subgroup. If we denote by
$P \leq G$
is any minimal parabolic subgroup. If we denote by
![]() $\operatorname {\mathrm {\mathcal {X}}}_G$
the Riemannian symmetric space associated to G, then usually the Furstenberg–Poisson boundary
$\operatorname {\mathrm {\mathcal {X}}}_G$
the Riemannian symmetric space associated to G, then usually the Furstenberg–Poisson boundary
![]() $B(G)$
is strictly contained in the boundary at infinity
$B(G)$
is strictly contained in the boundary at infinity
![]() $\partial _\infty \operatorname {\mathrm {\mathcal {X}}}_G$
. However, when G has real rank 1, the two coincide since it holds that
$\partial _\infty \operatorname {\mathrm {\mathcal {X}}}_G$
. However, when G has real rank 1, the two coincide since it holds that
Endow now
![]() $B(G)$
with its natural Borel structure coming from the Haar sigma-algebra on G and suppose that H acts measurably on a compact completely metrisable space Y.
$B(G)$
with its natural Borel structure coming from the Haar sigma-algebra on G and suppose that H acts measurably on a compact completely metrisable space Y.
Definition 2.4. Let
![]() $\sigma :G \times X \rightarrow H$
be a measurable cocycle. A measurable map
$\sigma :G \times X \rightarrow H$
be a measurable cocycle. A measurable map
![]() $\phi :B(G) \times X \rightarrow Y$
is
$\phi :B(G) \times X \rightarrow Y$
is
![]() $\sigma $
-equivariant if it holds that
$\sigma $
-equivariant if it holds that
for all
![]() $g \in G$
and almost every
$g \in G$
and almost every
![]() $\xi \in B(G)$
and
$\xi \in B(G)$
and
![]() $x \in X$
. A generalised boundary map (or simply boundary map) is the datum of a measurable map
$x \in X$
. A generalised boundary map (or simply boundary map) is the datum of a measurable map
![]() $\phi $
which is
$\phi $
which is
![]() $\sigma $
-equivariant.
$\sigma $
-equivariant.
The existence and the uniqueness of boundary maps for a measurable cocycle
![]() $\sigma $
usually rely on the properties of the cocycle. For instance, the proximality of the cocycle guarantees the existence of such a map. We are not going to define proximality here and we refer the reader to [Reference Furstenberg30] for a detailed exposition.
$\sigma $
usually rely on the properties of the cocycle. For instance, the proximality of the cocycle guarantees the existence of such a map. We are not going to define proximality here and we refer the reader to [Reference Furstenberg30] for a detailed exposition.
Since we introduce the notion of cohomologous cocycles, it is natural to show how boundary maps change along the H-cohomology class of a fixed cocycle.
Definition 2.5. Let
![]() $\sigma :G \times X \rightarrow H$
be a measurable cocycle with (generalised) boundary map
$\sigma :G \times X \rightarrow H$
be a measurable cocycle with (generalised) boundary map
![]() $\phi :B(G) \times X \rightarrow Y$
. Let
$\phi :B(G) \times X \rightarrow Y$
. Let
![]() $f:X \rightarrow H$
be a measurable map. The boundary map associated to the twisted cocycle
$f:X \rightarrow H$
be a measurable map. The boundary map associated to the twisted cocycle
![]() $\sigma ^f$
is given by
$\sigma ^f$
is given by
for almost every
![]() $\xi \in B(G)$
and
$\xi \in B(G)$
and
![]() $x \in X$
.
$x \in X$
.
We conclude this section by introducing the notion of slice associated to a boundary map. We will need this definition since we are going to assume the atomless property of the slices of a boundary map in order to construct our natural map.
Definition 2.6. Let
![]() $\sigma :G \times X \rightarrow H$
be a measurable cocycle and let
$\sigma :G \times X \rightarrow H$
be a measurable cocycle and let
![]() $\phi :B(G) \times X \rightarrow Y$
be a (generalised) boundary map. For almost every
$\phi :B(G) \times X \rightarrow Y$
be a (generalised) boundary map. For almost every
![]() $x \in X$
we define the slice associated to the point x as follows:
$x \in X$
we define the slice associated to the point x as follows:
for almost every
![]() $\xi \in B(G)$
.
$\xi \in B(G)$
.
By the equivariance of the map
![]() $\phi $
the slices are related by the following equation:
$\phi $
the slices are related by the following equation:
for every
![]() $g \in G$
and almost every
$g \in G$
and almost every
![]() $x \in X$
.
$x \in X$
.
It is worth noticing that for almost every
![]() $x \in X$
the slice
$x \in X$
the slice
![]() $\phi _x$
is measurable. Indeed, since we assumed that X is a standard Borel space, we know that the function
$\phi _x$
is measurable. Indeed, since we assumed that X is a standard Borel space, we know that the function
![]() $\widehat {\phi }:X \rightarrow \textrm {Meas}(B(G),Y), \hspace {5pt} \widehat {\phi }(x):=\phi _x,$
is well-defined and measurable by [Reference Feldman and Moore22, Lemma 2.6].
$\widehat {\phi }:X \rightarrow \textrm {Meas}(B(G),Y), \hspace {5pt} \widehat {\phi }(x):=\phi _x,$
is well-defined and measurable by [Reference Feldman and Moore22, Lemma 2.6].
2.2 Barycenter of a probability measure
In this section we are going to recall the barycenter construction introduced by Douady and Earle in their paper [Reference Derbez, Liu, Sun and Wang19]. As in the classic case of Besson, Courtois and Gallot, this machinery will be crucial to constructing our natural map.
Before giving the definition of the barycenter, we first need to recall the notion of Busemann function. Let
![]() $b \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
a fixed basepoint. The Busemann function pointed at b is the function given by
$b \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
a fixed basepoint. The Busemann function pointed at b is the function given by
where
![]() $c:[0,\infty ) \rightarrow \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
is a geodesic ray starting at
$c:[0,\infty ) \rightarrow \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
is a geodesic ray starting at
![]() $c(0)=b$
and ending at
$c(0)=b$
and ending at
![]() $\xi $
. The distance d is the one induced by the standard Riemannian structure on the hyperbolic space
$\xi $
. The distance d is the one induced by the standard Riemannian structure on the hyperbolic space
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Fix now a basepoint
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Fix now a basepoint
![]() $o \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. By an abuse of notation we will use the same symbol for the basepoint o in hyperbolic spaces of different dimensions. We are going to denote by
$o \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. By an abuse of notation we will use the same symbol for the basepoint o in hyperbolic spaces of different dimensions. We are going to denote by
![]() $\beta _o(x,\xi )$
the Busemann function pointed at the basepoint
$\beta _o(x,\xi )$
the Busemann function pointed at the basepoint
![]() $o \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
.
$o \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
.
Given any topological space X, denote by
![]() $\operatorname {\mathrm {\mathcal {M}}}^1(X)$
the space of positive probability measures on X. Consider now any positive probability measure
$\operatorname {\mathrm {\mathcal {M}}}^1(X)$
the space of positive probability measures on X. Consider now any positive probability measure
![]() $\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
on the boundary at infinity of the hyperbolic space. For our purposes, it will be sufficient to consider the case when
$\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
on the boundary at infinity of the hyperbolic space. For our purposes, it will be sufficient to consider the case when
![]() $\nu $
does not contain any atom. A crucial property of Busemann functions is given by their convexity (see [Reference Papadopoulos42, Chapter 8]). Using this property we get immediately that the function
$\nu $
does not contain any atom. A crucial property of Busemann functions is given by their convexity (see [Reference Papadopoulos42, Chapter 8]). Using this property we get immediately that the function
 $$ \begin{align*}\Lambda_\nu: \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}} \rightarrow \operatorname{\mathrm{\mathbb{R}}}, \hspace{5pt} \Lambda_\nu(x):=\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \beta_o(x,\xi)d\nu(\xi) \end{align*} $$
$$ \begin{align*}\Lambda_\nu: \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}} \rightarrow \operatorname{\mathrm{\mathbb{R}}}, \hspace{5pt} \Lambda_\nu(x):=\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \beta_o(x,\xi)d\nu(\xi) \end{align*} $$
is convex. Moreover, since the following condition holds,
the function
![]() $\Lambda _\nu $
attains its minimum inside
$\Lambda _\nu $
attains its minimum inside
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The uniqueness of such minimum is guaranteed by the fact that
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The uniqueness of such minimum is guaranteed by the fact that
![]() $\nu $
does not have any atom. We refer the reader to either [Reference Besson, Courtois and Gallot6, Appendix A] or [Reference Besson, Courtois and Gallot8, Proposition 3.7].
$\nu $
does not have any atom. We refer the reader to either [Reference Besson, Courtois and Gallot6, Appendix A] or [Reference Besson, Courtois and Gallot8, Proposition 3.7].
Definition 2.7. Let
![]() $\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
be a positive probability measure which does not contain any atom. The barycenter of the measure
$\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
be a positive probability measure which does not contain any atom. The barycenter of the measure
![]() $\nu $
is defined as
$\nu $
is defined as
Notice that the subscript
![]() $\operatorname {\mathrm {\mathcal {B}}}$
we used in the definition emphasises the dependence of the barycenter construction on the Busemann functions.
$\operatorname {\mathrm {\mathcal {B}}}$
we used in the definition emphasises the dependence of the barycenter construction on the Busemann functions.
Under the assumptions we made on the probability measure
![]() $\nu $
, its barycenter
$\nu $
, its barycenter
![]() $\operatorname {\mathrm {\textrm {bar}_{\mathcal {B}}}}(\nu )$
will be a point in
$\operatorname {\mathrm {\textrm {bar}_{\mathcal {B}}}}(\nu )$
will be a point in
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which satisfies the following properties:
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which satisfies the following properties:
-
(i): the barycenter is continuous with respect to the weak-
 ${}^*$
topology on the space
${}^*$
topology on the space
 $\operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
. More precisely, if
$\operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
. More precisely, if
 $\nu _k \rightarrow \nu $
in the weak-
$\nu _k \rightarrow \nu $
in the weak-
 ${}^*$
topology, it holds that
${}^*$
topology, it holds that  $$ \begin{align*}\lim_{k \to \infty} \operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu_k)=\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu) \; \end{align*} $$
$$ \begin{align*}\lim_{k \to \infty} \operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu_k)=\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu) \; \end{align*} $$
-
(ii): the barycenter is
 $\operatorname {\mathrm {{\rm G}}}(n)$
-equivariant. Recall first that
$\operatorname {\mathrm {{\rm G}}}(n)$
-equivariant. Recall first that
 $\operatorname {\mathrm {{\rm G}}}(n)$
is the isometry group of the Riemannian symmetric space
$\operatorname {\mathrm {{\rm G}}}(n)$
is the isometry group of the Riemannian symmetric space
 $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Then for every
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Then for every
 $g \in \operatorname {\mathrm {{\rm G}}}(n)$
we have that for every
$g \in \operatorname {\mathrm {{\rm G}}}(n)$
we have that for every $$ \begin{align*}\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(g_*\nu)=g\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu) \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(g_*\nu)=g\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu) \end{align*} $$
 $\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
. The symbol
$\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
. The symbol
 $g_*\nu $
stands for the push-forward measure of
$g_*\nu $
stands for the push-forward measure of
 $\nu $
with respect to the isometry g;
$\nu $
with respect to the isometry g;
-
(iii): the barycenter satisfies an implicit equation given by
(4)where $$ \begin{align} \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu),\xi)}( \cdot )d\nu(\xi)=0 , \end{align} $$
$$ \begin{align} \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\nu),\xi)}( \cdot )d\nu(\xi)=0 , \end{align} $$
 $\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
and
$\nu \in \operatorname {\mathrm {\mathcal {M}}}^1(\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
and
 $d\beta _o$
denotes the differential of the Busemann function pointed at
$d\beta _o$
denotes the differential of the Busemann function pointed at
 $o \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. This property will be crucial to proving the smoothness of the slices of our natural map and to obtaining the estimate on the Jacobian.
$o \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. This property will be crucial to proving the smoothness of the slices of our natural map and to obtaining the estimate on the Jacobian.
2.3 Family of Patterson–Sullivan measures and BCG natural map
In this section we are going to recall the definition of Patterson–Sullivan measures and the notion of natural map associated to a representation. We refer the reader to [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8, Reference Francaviglia25, Reference Fisher, Morris and Whyte24] for a more detailed exposition about these notions.
Let
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
be equal to either
$\operatorname {\mathrm {{\rm G}}}(n)$
be equal to either
![]() $\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
$\operatorname {\mathrm {{\rm PO}}}(n,1),\operatorname {\mathrm {{\rm PU}}}(n,1)$
or
![]() $\operatorname {\mathrm {{\rm PSp}}}(n,1)$
. It is well-known that the Riemannian symmetric space associated to the rank 1 Lie group
$\operatorname {\mathrm {{\rm PSp}}}(n,1)$
. It is well-known that the Riemannian symmetric space associated to the rank 1 Lie group
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
is the hyperbolic space
$\operatorname {\mathrm {{\rm G}}}(n)$
is the hyperbolic space
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
on a suitable division algebra
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
on a suitable division algebra
![]() $\operatorname {\mathrm {{\rm K}}}$
. More precisely, we have that
$\operatorname {\mathrm {{\rm K}}}$
. More precisely, we have that
![]() $\operatorname {\mathrm {{\rm K}}}=\operatorname {\mathrm {\mathbb {R}}}$
if
$\operatorname {\mathrm {{\rm K}}}=\operatorname {\mathrm {\mathbb {R}}}$
if
![]() $\operatorname {\mathrm {{\rm G}}}(n)=\operatorname {\mathrm {{\rm PO}}}(n,1)$
,
$\operatorname {\mathrm {{\rm G}}}(n)=\operatorname {\mathrm {{\rm PO}}}(n,1)$
,
![]() $\operatorname {\mathrm {{\rm K}}}=\operatorname {\mathrm {\mathbb {C}}}$
if
$\operatorname {\mathrm {{\rm K}}}=\operatorname {\mathrm {\mathbb {C}}}$
if
![]() $\operatorname {\mathrm {{\rm G}}}(n)=\operatorname {\mathrm {{\rm PU}}}(n,1)$
and
$\operatorname {\mathrm {{\rm G}}}(n)=\operatorname {\mathrm {{\rm PU}}}(n,1)$
and
![]() $\operatorname {\mathrm {{\rm K}}}=\operatorname {\mathrm {\mathbb {H}}}$
if
$\operatorname {\mathrm {{\rm K}}}=\operatorname {\mathrm {\mathbb {H}}}$
if
![]() $\operatorname {\mathrm {{\rm G}}}(n)=\operatorname {\mathrm {{\rm PSp}}}(n,1)$
. In all of these cases, we are going to normalise the Riemannian metric on
$\operatorname {\mathrm {{\rm G}}}(n)=\operatorname {\mathrm {{\rm PSp}}}(n,1)$
. In all of these cases, we are going to normalise the Riemannian metric on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
so that the sectional curvature has maximum value equal to
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
so that the sectional curvature has maximum value equal to
![]() $-1$
. Denote by
$-1$
. Denote by
![]() $d=\dim _{\operatorname {\mathrm {\mathbb {R}}}}\operatorname {\mathrm {{\rm K}}}$
and assume that
$d=\dim _{\operatorname {\mathrm {\mathbb {R}}}}\operatorname {\mathrm {{\rm K}}}$
and assume that
![]() $d(n-1)\geq 2$
.
$d(n-1)\geq 2$
.
Fix now a torsion-free (uniform) lattice
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
.
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
.
Definition 2.8. Let
![]() $x \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
be any point and let
$x \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
be any point and let
![]() $s>0$
be a real number. The s-Poincaré series pointed at x is given by the following sum:
$s>0$
be a real number. The s-Poincaré series pointed at x is given by the following sum:
where d stands for the distance induced by the fixed Riemannian structure on the space
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The critical exponent associated to the lattice
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The critical exponent associated to the lattice
![]() $\Gamma $
is defined as
$\Gamma $
is defined as
The definition of critical exponent does not depend on the choice of the particular point
![]() $x \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
we fixed.
$x \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
we fixed.
The critical exponent associated to a torsion-free (uniform) lattice in a rank-1 Lie group is always finite and equal to
as shown, for instance, in [Reference Albuquerque2, Theorem 2]. We remind the reader that when
![]() $s=\delta _\Gamma $
the Poincaré series
$s=\delta _\Gamma $
the Poincaré series
![]() $\operatorname {\mathrm {\mathcal {P}}}(s;x)$
diverges – that is,
$\operatorname {\mathrm {\mathcal {P}}}(s;x)$
diverges – that is,
![]() $\operatorname {\mathrm {\mathcal {P}}}(\delta _\Gamma ;x)=+\infty $
[Reference Sullivan49, Reference Boland and Newberger14, Reference Yue51] – and for this reason we call
$\operatorname {\mathrm {\mathcal {P}}}(\delta _\Gamma ;x)=+\infty $
[Reference Sullivan49, Reference Boland and Newberger14, Reference Yue51] – and for this reason we call
![]() $\Gamma $
a group of divergence type.
$\Gamma $
a group of divergence type.
Now we are ready to give the definition of Patterson–Sullivan measures. This notion fits into a more general concept of conformal density.
Definition 2.9. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free (uniform) lattice. Fix a positive real number
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free (uniform) lattice. Fix a positive real number
![]() $\alpha>0$
. An
$\alpha>0$
. An
![]() $\alpha $
-conformal density for the lattice
$\alpha $
-conformal density for the lattice
![]() $\Gamma $
is a measurable map
$\Gamma $
is a measurable map
which satisfies the following conditions:
-
(i): it is
 $\Gamma $
-equivariant; that is,
$\Gamma $
-equivariant; that is,
 $\nu _{\gamma a}=\gamma _\ast \nu _a$
for every
$\nu _{\gamma a}=\gamma _\ast \nu _a$
for every
 $\gamma \in \Gamma $
and every
$\gamma \in \Gamma $
and every
 $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The symbol
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. The symbol
 $\gamma _\ast $
stands for the push-forward measure with respect to
$\gamma _\ast $
stands for the push-forward measure with respect to
 $\gamma $
.
$\gamma $
. -
(ii): given two different points
 $a,b \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, the measure
$a,b \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, the measure
 $\nu _a$
is absolutely continuous with respect to
$\nu _a$
is absolutely continuous with respect to
 $\nu _b$
and the Radon–Nikodym derivative is given by where
$\nu _b$
and the Radon–Nikodym derivative is given by where $$ \begin{align*}\frac{d\nu_a}{d\nu_b}(\xi)=e^{-\alpha \beta_b(a,\xi)} , \end{align*} $$
$$ \begin{align*}\frac{d\nu_a}{d\nu_b}(\xi)=e^{-\alpha \beta_b(a,\xi)} , \end{align*} $$
 $\xi \in \partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
$\xi \in \partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
 $\beta _b(a,\xi )$
is the Busemann function pointed at b.
$\beta _b(a,\xi )$
is the Busemann function pointed at b.
When
![]() $\alpha $
is equal to the critical exponent
$\alpha $
is equal to the critical exponent
![]() $\delta _\Gamma $
, the
$\delta _\Gamma $
, the
![]() $\delta _\Gamma $
-conformal density associated to
$\delta _\Gamma $
-conformal density associated to
![]() $\Gamma $
is called the Patterson–Sullivan density.
$\Gamma $
is called the Patterson–Sullivan density.
Given a lattice
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
, there always exists a Patterson–Sullivan density associated to it. Moreover, it is essentially unique by the doubly ergodic action of
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
, there always exists a Patterson–Sullivan density associated to it. Moreover, it is essentially unique by the doubly ergodic action of
![]() $\Gamma $
on the boundary at infinity
$\Gamma $
on the boundary at infinity
![]() $\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(see, for instance, [Reference Sullivan49, Reference Neumann and Zagier41, Reference Boland and Newberger14, Reference Roblin43, Reference Fisher, Morris and Whyte24]). It is worth mentioning that the construction of the Patterson–Sullivan density has been extended by Albuquerque [Reference Albuquerque2, Reference Albuquerque3] to higher rank lattices in a semisimple Lie group G of noncompact type. In the higher rank case the support of the measures is strictly smaller than the boundary at infinity of symmetric space
$\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(see, for instance, [Reference Sullivan49, Reference Neumann and Zagier41, Reference Boland and Newberger14, Reference Roblin43, Reference Fisher, Morris and Whyte24]). It is worth mentioning that the construction of the Patterson–Sullivan density has been extended by Albuquerque [Reference Albuquerque2, Reference Albuquerque3] to higher rank lattices in a semisimple Lie group G of noncompact type. In the higher rank case the support of the measures is strictly smaller than the boundary at infinity of symmetric space
![]() $\operatorname {\mathrm {\mathcal {X}}}_G$
associated to G. Indeed, the support can be identified with the Furstenberg–Poisson boundary
$\operatorname {\mathrm {\mathcal {X}}}_G$
associated to G. Indeed, the support can be identified with the Furstenberg–Poisson boundary
![]() $B(G)$
(see Subsection 2.1 for the definition).
$B(G)$
(see Subsection 2.1 for the definition).
We conclude the section by recalling briefly the construction of the natural map associated to a representation. This can help the reader to understand how we are going to adapt the construction to the case of measurable cocycles. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be as above and consider
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be as above and consider
![]() $\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
a non-elementary representation, with
$\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
a non-elementary representation, with
![]() $d(n-1)\geq 2$
and
$d(n-1)\geq 2$
and
![]() $m \geq n$
. Denote by
$m \geq n$
. Denote by
![]() $\{ \nu _a \}_{a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}}$
the Patterson–Sullivan density of measure (actually its image).
$\{ \nu _a \}_{a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}}$
the Patterson–Sullivan density of measure (actually its image).
Since the representation
![]() $\rho $
is non-elementary, by [Reference Boland and Newberger14, Corollary 3.2] there exists a measurable
$\rho $
is non-elementary, by [Reference Boland and Newberger14, Corollary 3.2] there exists a measurable
![]() $\rho $
-equivariant map
$\rho $
-equivariant map
Additionally, this map is essentially injective by both [Reference Francaviglia26, Lemma 2.3] and [Reference Savini44, Lemma 2.5]. This implies that for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the push-forward measure
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the push-forward measure
![]() $\varphi _\ast (\nu _a)$
has no atom. This condition allows us to define the Besson–Courtois–Gallot natural map associated to
$\varphi _\ast (\nu _a)$
has no atom. This condition allows us to define the Besson–Courtois–Gallot natural map associated to
![]() $\rho $
.
$\rho $
.
Definition 2.10. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a (uniform) lattice and let
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a (uniform) lattice and let
![]() $\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a non-elementary representation, with
$\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a non-elementary representation, with
![]() $d(n-1)\geq 2$
and
$d(n-1)\geq 2$
and
![]() $m \geq n$
. If
$m \geq n$
. If
![]() $\varphi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is the associated measurable map, we define the natural map associated to
$\varphi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is the associated measurable map, we define the natural map associated to
![]() $\rho $
as follows:
$\rho $
as follows:
The map defined above is smooth and
![]() $\rho $
-equivariant; that is,
$\rho $
-equivariant; that is,
![]() $F(\gamma a)=\rho (\gamma )F(a)$
for every
$F(\gamma a)=\rho (\gamma )F(a)$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. For every positive integer
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. For every positive integer
![]() $p \in \operatorname {\mathrm {\mathbb {N}}}$
, we define the p-Jacobian of F at a as
$p \in \operatorname {\mathrm {\mathbb {N}}}$
, we define the p-Jacobian of F at a as
where
![]() $\{ u_1,\ldots ,u_p\}$
is an orthonormal p-frame on the tangent space
$\{ u_1,\ldots ,u_p\}$
is an orthonormal p-frame on the tangent space
![]() $T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
with respect to the standard Riemannian metric
$T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
with respect to the standard Riemannian metric
![]() $g_n$
and
$g_n$
and
![]() $\lVert \ \cdot \ \rVert _m$
stands for the norm induced by
$\lVert \ \cdot \ \rVert _m$
stands for the norm induced by
![]() $g_m$
. When
$g_m$
. When
![]() $p=n \cdot d$
– that is, it is equal to the real dimension of
$p=n \cdot d$
– that is, it is equal to the real dimension of
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
– we are going to denote the p-Jacobian simply by
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
– we are going to denote the p-Jacobian simply by
![]() $\operatorname {\mathrm {\textrm {Jac}}}_aF$
. For the natural map
$\operatorname {\mathrm {\textrm {Jac}}}_aF$
. For the natural map
![]() $F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
it holds that
$F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
it holds that
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and the equality is attained if and only if the map
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and the equality is attained if and only if the map
![]() $D_aF:T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow T_{F(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is an isometric embedding (see [Reference Besson, Courtois and Gallot6, Lemma 7.2] for a proof of the inequality and [Reference Besson, Courtois and Gallot6, Appendix B] for the study of the equality case).
$D_aF:T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow T_{F(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is an isometric embedding (see [Reference Besson, Courtois and Gallot6, Lemma 7.2] for a proof of the inequality and [Reference Besson, Courtois and Gallot6, Appendix B] for the study of the equality case).
Since the natural map is defined using the barycenter and the latter satisfies Equation (4), in this context one can verify that it holds that
 $$ \begin{align} \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F(a),\varphi(\xi))} ( \ \cdot \ )d\nu_a(\xi)=0 . \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F(a),\varphi(\xi))} ( \ \cdot \ )d\nu_a(\xi)=0 . \\[-15pt]\nonumber\end{align} $$
By differentiating the previous equation, for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}, u \in T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}, v \in T_{F(a)} \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
one obtains that
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}, u \in T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}, v \in T_{F(a)} \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
one obtains that
 $$ \begin{align} &\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \nabla d\beta_o|_{(F(a),\varphi(\xi))} (D_aF(u),v)d\nu_a(\xi)=\nonumber\\ &=\delta_\Gamma \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F(a),\varphi(\xi))} (v) d\beta_o|_{(a,\xi)}(u)d\nu_a(\xi) . \\[-15pt]\nonumber\end{align} $$
$$ \begin{align} &\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \nabla d\beta_o|_{(F(a),\varphi(\xi))} (D_aF(u),v)d\nu_a(\xi)=\nonumber\\ &=\delta_\Gamma \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F(a),\varphi(\xi))} (v) d\beta_o|_{(a,\xi)}(u)d\nu_a(\xi) . \\[-15pt]\nonumber\end{align} $$
Here
![]() $\nabla $
is the Levi–Civita connection associated to the natural Riemannian metric on
$\nabla $
is the Levi–Civita connection associated to the natural Riemannian metric on
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. We warn the reader that the Busemann functions that appear in the second line of the equation above refer to hyperbolic spaces of different dimensions (the first is defined on
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. We warn the reader that the Busemann functions that appear in the second line of the equation above refer to hyperbolic spaces of different dimensions (the first is defined on
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
and the second one on
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
and the second one on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
).
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
).
3 Natural maps associated to Zimmer cocycles
In this section we are going to define the natural map associated to a measurable cocycle of a uniform hyperbolic lattice. The key point in the construction will be to consider measurable cocycles which admit a boundary map whose slices are atomless; that is, the push-forward of the Patterson–Sullivan measure has no atom. This assumption will allow us to mimic the techniques used for non-elementary representations.
Proof of Theorem 1.1. Given
![]() $x \in X$
, consider
$x \in X$
, consider
the slice of the boundary map
![]() $\phi $
. For any
$\phi $
. For any
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, let
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, let
![]() $\nu _a$
be the Patterson–Sullivan measure pointed at a. If we consider the push-forward measure
$\nu _a$
be the Patterson–Sullivan measure pointed at a. If we consider the push-forward measure
![]() $(\phi _x)_*(\nu _a)$
, this has no atoms by assumption. Hence, we can apply the barycenter to define our desired map. More precisely, define
$(\phi _x)_*(\nu _a)$
, this has no atoms by assumption. Hence, we can apply the barycenter to define our desired map. More precisely, define
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
![]() $x \in X$
.
$x \in X$
.
Clearly, the map F is well-defined by what we have said so far. Now we prove the
![]() $\sigma $
-equivariance. Notice first that for almost every
$\sigma $
-equivariance. Notice first that for almost every
![]() $x \in X$
we have a map
$x \in X$
we have a map
![]() $F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
given by
$F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
given by
![]() $F_x(a):=F(a,x)$
. We call this map the x-slice of the map F. Additionally, we can suppose that the full-measure subset of X on which the slices of F are defined is
$F_x(a):=F(a,x)$
. We call this map the x-slice of the map F. Additionally, we can suppose that the full-measure subset of X on which the slices of F are defined is
![]() $\Gamma $
-invariant. Hence, given
$\Gamma $
-invariant. Hence, given
![]() $\gamma \in \Gamma $
, it holds that
$\gamma \in \Gamma $
, it holds that
 $$ \begin{align*} F(\gamma a,\gamma x)=&\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}((\phi_{\gamma x})_\ast(\nu_{\gamma a}))=\\ =&\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}((\phi_{\gamma x})_\ast(\gamma_\ast \nu_a))=\\ =&\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\sigma(\gamma,x)_\ast ((\phi_x)_\ast(\nu_a)))=\\ =&\sigma(\gamma,x)\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}((\phi_x)_\ast(\nu_a))=\sigma(\gamma,x)F(a,x) , \end{align*} $$
$$ \begin{align*} F(\gamma a,\gamma x)=&\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}((\phi_{\gamma x})_\ast(\nu_{\gamma a}))=\\ =&\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}((\phi_{\gamma x})_\ast(\gamma_\ast \nu_a))=\\ =&\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}(\sigma(\gamma,x)_\ast ((\phi_x)_\ast(\nu_a)))=\\ =&\sigma(\gamma,x)\operatorname{\mathrm{\textrm{bar}_{\mathcal{B}}}}((\phi_x)_\ast(\nu_a))=\sigma(\gamma,x)F(a,x) , \end{align*} $$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
![]() $x \in X$
. To pass from the first line to the second one we used the
$x \in X$
. To pass from the first line to the second one we used the
![]() $\Gamma $
-equivariance of the Patterson–Sullivan density and to move from the second line to the third one we exploited Equation (3). To conclude we used the fact that the barycenter is
$\Gamma $
-equivariance of the Patterson–Sullivan density and to move from the second line to the third one we exploited Equation (3). To conclude we used the fact that the barycenter is
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
-equivariant. The previous computation shows the
$\operatorname {\mathrm {{\rm G}}}(m)$
-equivariant. The previous computation shows the
![]() $\sigma $
-equivariance of the map F, as desired.
$\sigma $
-equivariance of the map F, as desired.
Since the barycenter is characterised by the implicit Equation (4), for almost every
![]() $x \in X$
we have that the slice
$x \in X$
we have that the slice
![]() $F_x$
satisfies the equation
$F_x$
satisfies the equation
 $$ \begin{align} \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F_x(a),\phi_x(\xi))}(\cdot)d\nu_a(\xi)=0 \end{align} $$
$$ \begin{align} \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F_x(a),\phi_x(\xi))}(\cdot)d\nu_a(\xi)=0 \end{align} $$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. By differentiating with respect to the variable a the previous equation, for almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. By differentiating with respect to the variable a the previous equation, for almost every
![]() $x \in X$
and every
$x \in X$
and every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}, u \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}},v \in T_{F_x(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
we obtain that
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}, u \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}},v \in T_{F_x(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
we obtain that
 $$ \begin{align} &\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \nabla d\beta_o|_{(F_x(a),\phi_x(\xi))} (D_aF_x(u),v)d\nu_a(\xi)=\nonumber\\ &=\delta_\Gamma \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F_x(a),\phi_x(\xi))} (v) d\beta_o|_{(a,\xi)}(u)d\nu_a(\xi) , \end{align} $$
$$ \begin{align} &\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \nabla d\beta_o|_{(F_x(a),\phi_x(\xi))} (D_aF_x(u),v)d\nu_a(\xi)=\nonumber\\ &=\delta_\Gamma \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} d\beta_o|_{(F_x(a),\phi_x(\xi))} (v) d\beta_o|_{(a,\xi)}(u)d\nu_a(\xi) , \end{align} $$
where
![]() $\nabla $
is the Levi–Civita connection on
$\nabla $
is the Levi–Civita connection on
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. Applying the same reasoning of Besson, Courtois and Gallot exposed in [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7] to the equation above one gets that the slice
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. Applying the same reasoning of Besson, Courtois and Gallot exposed in [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7] to the equation above one gets that the slice
![]() $F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is smooth for almost every
$F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is smooth for almost every
![]() $x \in X$
, as claimed.
$x \in X$
, as claimed.
We want to conclude by proving the estimate on the Jacobian of
![]() $F_x$
. Fix an x for which the slice
$F_x$
. Fix an x for which the slice
![]() $F_x$
is smooth. Recall that, for every
$F_x$
is smooth. Recall that, for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, we are allowed to define three quadratic forms, one on the tangent space
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, we are allowed to define three quadratic forms, one on the tangent space
![]() $T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and two on the tangent space
$T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and two on the tangent space
![]() $T_{F(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. More precisely, given
$T_{F(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. More precisely, given
![]() $u \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
$u \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
![]() $v \in T_{F_x(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
we define
$v \in T_{F_x(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
we define
 $$ \begin{align*} h^{\prime}_{a,x}(u,u)&:=\langle H^{\prime}_{a,x}(u),u \rangle_n=\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \left(d\beta_o|_{(a,\xi)}(u)\right)^2d\nu_a(\xi) , \\ h_{a,x}(v,v)&:=\langle H_{a,x}(v),v \rangle_m = \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \left(d\beta_o|_{(F_x(a),\phi_x(\xi))}\right)^2d\nu_a(\xi) , \\ k_{a,x}(v,v)&:=\langle K_{a,x}(v),v \rangle_m = \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \nabla d\beta_o|_{(F_x(a),\phi_x(\xi))}(v,v)d\nu_a(\xi) . \end{align*} $$
$$ \begin{align*} h^{\prime}_{a,x}(u,u)&:=\langle H^{\prime}_{a,x}(u),u \rangle_n=\int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \left(d\beta_o|_{(a,\xi)}(u)\right)^2d\nu_a(\xi) , \\ h_{a,x}(v,v)&:=\langle H_{a,x}(v),v \rangle_m = \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \left(d\beta_o|_{(F_x(a),\phi_x(\xi))}\right)^2d\nu_a(\xi) , \\ k_{a,x}(v,v)&:=\langle K_{a,x}(v),v \rangle_m = \int_{\partial_\infty \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \nabla d\beta_o|_{(F_x(a),\phi_x(\xi))}(v,v)d\nu_a(\xi) . \end{align*} $$
Here
![]() $H^{\prime }_{a,x},H_{a,x}$
and
$H^{\prime }_{a,x},H_{a,x}$
and
![]() $K_{a,x}$
are the endomorphisms associated to the symmetric bilinear forms with respect to the scalar product
$K_{a,x}$
are the endomorphisms associated to the symmetric bilinear forms with respect to the scalar product
![]() $\langle \cdot , \cdot \rangle _n$
(respectively
$\langle \cdot , \cdot \rangle _n$
(respectively
![]() $\langle \cdot ,\cdot \rangle _m$
) associated to the natural Riemannian metric on
$\langle \cdot ,\cdot \rangle _m$
) associated to the natural Riemannian metric on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(respectively
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(respectively
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
). It is worth noticing that both
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
). It is worth noticing that both
![]() $h_{a,x}$
and
$h_{a,x}$
and
![]() $h^{\prime }_{a,x}$
are positive semidefinite bilinear forms; thus, we are allowed to consider their square roots. As a consequence, applying the Cauchy–Schwarz inequality as in [Reference Besson, Courtois and Gallot8, Section 2] to Equation (9), we get
$h^{\prime }_{a,x}$
are positive semidefinite bilinear forms; thus, we are allowed to consider their square roots. As a consequence, applying the Cauchy–Schwarz inequality as in [Reference Besson, Courtois and Gallot8, Section 2] to Equation (9), we get
Let
![]() $V_{a,x}:=D_aF_x(T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
be the image of the tangent space through the derivative at a of the slice
$V_{a,x}:=D_aF_x(T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}})$
be the image of the tangent space through the derivative at a of the slice
![]() $F_x$
. Denote by
$F_x$
. Denote by
![]() $h^V_{a,x},k^V_{a,x}$
the restrictions of the bilinears forms
$h^V_{a,x},k^V_{a,x}$
the restrictions of the bilinears forms
![]() $h_{a,x},k_{a,x}$
to the subspace V. Let
$h_{a,x},k_{a,x}$
to the subspace V. Let
![]() $H^V_{a,x},K^V_{a,x}$
be the associated endomorphisms. Set
$H^V_{a,x},K^V_{a,x}$
be the associated endomorphisms. Set
![]() $p=d \cdot n$
. By taking the determinant of Equation (10), one gets the following sequence of estimates:
$p=d \cdot n$
. By taking the determinant of Equation (10), one gets the following sequence of estimates:
 $$ \begin{align*} \det(K^V_{a,x})\operatorname{\mathrm{\textrm{Jac}}}_aF_x &\leq (\delta_\Gamma)^{p}\left( \det H^V_{a,x} \right)^{\frac{1}{2}} \left( \det H_{a,x}' \right)^{\frac{1}{2}} \leq \\ &\leq (\delta_\Gamma)^{p} \left( \det H^{V}_{a,x} \right)^{\frac{1}{2}} \left( \operatorname{\mathrm{tr}} H^{\prime}_{a,x}/p\right)^{\frac{p}{2}} \leq \\ &\leq p^{-\frac{p}{2}}\cdot (\delta_\Gamma)^{p} \left( \det H^V_{a,x} \right)^{\frac{1}{2}}. \end{align*} $$
$$ \begin{align*} \det(K^V_{a,x})\operatorname{\mathrm{\textrm{Jac}}}_aF_x &\leq (\delta_\Gamma)^{p}\left( \det H^V_{a,x} \right)^{\frac{1}{2}} \left( \det H_{a,x}' \right)^{\frac{1}{2}} \leq \\ &\leq (\delta_\Gamma)^{p} \left( \det H^{V}_{a,x} \right)^{\frac{1}{2}} \left( \operatorname{\mathrm{tr}} H^{\prime}_{a,x}/p\right)^{\frac{p}{2}} \leq \\ &\leq p^{-\frac{p}{2}}\cdot (\delta_\Gamma)^{p} \left( \det H^V_{a,x} \right)^{\frac{1}{2}}. \end{align*} $$
It is worth noticing that the estimate above depends on a suitable choice of basis of both
![]() $T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
$T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
![]() $V_{a,x}$
. We refer the reader to [Reference Besson, Courtois and Gallot8, Lemma 5.3] for more details.
$V_{a,x}$
. We refer the reader to [Reference Besson, Courtois and Gallot8, Lemma 5.3] for more details.
Finally, by applying [Reference Besson, Courtois and Gallot6, Proposition B.1], we obtain that
 $$ \begin{align*}\operatorname{\mathrm{\textrm{Jac}}}_aF_x \leq \frac{ (\delta_\Gamma)^{p} }{p^{-\frac{p}{2}}} \frac{ \left(\det H^V_{a,x} \right)^{\frac{1}{2}}}{\det(K^V_{a,x})} \leq 1 , \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{\textrm{Jac}}}_aF_x \leq \frac{ (\delta_\Gamma)^{p} }{p^{-\frac{p}{2}}} \frac{ \left(\det H^V_{a,x} \right)^{\frac{1}{2}}}{\det(K^V_{a,x})} \leq 1 , \end{align*} $$
and the desired estimate is proved. When the equality is attained, the proof that
![]() $D_aF_x:T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow T_{F_x(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is an isometric embedding is analogous to the one exposed in [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] and hence we omit it.
$D_aF_x:T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow T_{F_x(a)}\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
is an isometric embedding is analogous to the one exposed in [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] and hence we omit it.
Remark 3.1. Notice that in the proof of Theorem 1.1 we never use the uniformity of the lattice
![]() $\Gamma $
. This implies that the same construction can be suitably extended also to torsion-free nonuniform lattices. In the latter case one would like to prove a property similar to the properly ending condition defined in [Reference Francaviglia25, Reference Fisher, Morris and Whyte24]. However, we cannot understand a clear way to do it in this context.
$\Gamma $
. This implies that the same construction can be suitably extended also to torsion-free nonuniform lattices. In the latter case one would like to prove a property similar to the properly ending condition defined in [Reference Francaviglia25, Reference Fisher, Morris and Whyte24]. However, we cannot understand a clear way to do it in this context.
Remark 3.2. One could ask when a boundary map has atomless slices and how restrictive this hypothesis is. When
![]() $\sigma $
is the measurable cocycle associated to a self-coupling of a uniform lattice
$\sigma $
is the measurable cocycle associated to a self-coupling of a uniform lattice
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
, the slices of the boundary map are atomless by either [Reference Bucher, Burger and Iozzi4, Lemma 3.6] or [Reference Savini48, Lemma 3.1]. More generally, if
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
, the slices of the boundary map are atomless by either [Reference Bucher, Burger and Iozzi4, Lemma 3.6] or [Reference Savini48, Lemma 3.1]. More generally, if
![]() $(X,\mu _X)$
is ergodic and the cocycle is Zariski dense, this is sufficient to guarantee atomless slices.
$(X,\mu _X)$
is ergodic and the cocycle is Zariski dense, this is sufficient to guarantee atomless slices.
Recall that in Subsection 2.1 we discussed how to construct a suitable measurable cocycle starting from a representation
![]() $\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
once we fixed a standard Borel probability
$\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
once we fixed a standard Borel probability
![]() $\Gamma $
-space. One could naturally ask whether there exists a relation between the natural map associated to
$\Gamma $
-space. One could naturally ask whether there exists a relation between the natural map associated to
![]() $\rho $
defined in [Reference Francaviglia25, Reference Fisher, Morris and Whyte24] and the natural map we defined in Theorem 1.1. Their link is given by the following.
$\rho $
defined in [Reference Francaviglia25, Reference Fisher, Morris and Whyte24] and the natural map we defined in Theorem 1.1. Their link is given by the following.
Proposition 3.3. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and let
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and let
![]() $\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a non-elementary representation, with
$\rho :\Gamma \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a non-elementary representation, with
![]() $m \geq n$
. Fix a standard Borel probability
$m \geq n$
. Fix a standard Borel probability
![]() $\Gamma $
-space
$\Gamma $
-space
![]() $(X,\mu _X)$
. Denote by
$(X,\mu _X)$
. Denote by
![]() $\widetilde {F}:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
and by
$\widetilde {F}:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
and by
![]() $\sigma _\rho :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
the natural map and the measurable cocycle associated to
$\sigma _\rho :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
the natural map and the measurable cocycle associated to
![]() $\rho $
, respectively. Then the natural map associated to
$\rho $
, respectively. Then the natural map associated to
![]() $\sigma _\rho $
is given by
$\sigma _\rho $
is given by
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
![]() $x \in X$
.
$x \in X$
.
Proof. Since
![]() $\rho $
is non-elementary, by [Reference Boland and Newberger14, Reference Fisher, Morris and Whyte24] there exists a measurable boundary map
$\rho $
is non-elementary, by [Reference Boland and Newberger14, Reference Fisher, Morris and Whyte24] there exists a measurable boundary map
![]() $\widetilde {\varphi }:\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
which is
$\widetilde {\varphi }:\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
which is
![]() $\rho $
-equivariant. Additionally, since the
$\rho $
-equivariant. Additionally, since the
![]() $\Gamma $
action on the boundary
$\Gamma $
action on the boundary
![]() $\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
is doubly ergodic, the map is essentially unique ([Reference Sullivan49, Reference Neumann and Zagier41, Reference Boland and Newberger14, Reference Roblin43, Reference Fisher, Morris and Whyte24]) and essentially injective ([Reference Francaviglia26, Lemma 2.3],[Reference Savini44, Lemma 2.5]).
$\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
is doubly ergodic, the map is essentially unique ([Reference Sullivan49, Reference Neumann and Zagier41, Reference Boland and Newberger14, Reference Roblin43, Reference Fisher, Morris and Whyte24]) and essentially injective ([Reference Francaviglia26, Lemma 2.3],[Reference Savini44, Lemma 2.5]).
The previous map allows one to define an essentially unique boundary map associated to
![]() $\sigma _\rho $
as follows:
$\sigma _\rho $
as follows:
for almost every
![]() $\xi \in X$
and every
$\xi \in X$
and every
![]() $x \in X$
. Moreover, since every slice
$x \in X$
. Moreover, since every slice
![]() $\phi _x$
coincides with the map
$\phi _x$
coincides with the map
![]() $\widetilde {\varphi }$
, every slice is essentially injective. Hence, we are in the hypothesis of Theorem 1.1 and we are allowed to construct the natural map associated to
$\widetilde {\varphi }$
, every slice is essentially injective. Hence, we are in the hypothesis of Theorem 1.1 and we are allowed to construct the natural map associated to
![]() $\sigma _\rho $
. By definition we have that
$\sigma _\rho $
. By definition we have that
and the claim is proved.
We conclude the section by showing how natural maps change in the
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class of a given measurable cocycle.
$\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class of a given measurable cocycle.
Proposition 3.4. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
![]() $(X,\mu _X)$
a standard Borel probability
$(X,\mu _X)$
a standard Borel probability
![]() $\Gamma $
-space. Let
$\Gamma $
-space. Let
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a measurable cocycle which admits a natural map
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a measurable cocycle which admits a natural map
![]() $F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. Given a measurable map
$F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. Given a measurable map
![]() $f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, the natural map associated to the cocycle
$f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, the natural map associated to the cocycle
![]() $\sigma ^f$
is given by
$\sigma ^f$
is given by
Proof. Denote by
![]() $\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
the boundary map associated to
$\phi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
the boundary map associated to
![]() $\sigma $
. Recall by Definitions 2.2 and 2.5 that the twisted cocycle
$\sigma $
. Recall by Definitions 2.2 and 2.5 that the twisted cocycle
admits as boundary map
Notice that f takes values into
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
; hence, if almost every slice of
$\operatorname {\mathrm {{\rm G}}}(m)$
; hence, if almost every slice of
![]() $\phi $
is atomless, the same holds for
$\phi $
is atomless, the same holds for
![]() $\phi ^f$
. By definition of the associated natural map we have
$\phi ^f$
. By definition of the associated natural map we have
Since the barycenter is
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
-equivariant, we obtain
$\operatorname {\mathrm {{\rm G}}}(m)$
-equivariant, we obtain
and the statement follows.
4 Natural volume of Zimmer cocycles
In this section we are going to introduce the notion of natural volume of a measurable cocycle of a uniform hyperbolic lattice. As already discussed in the Introduction, even if we are going to focus our attention only on uniform lattices, the same results of the section will hold also in the nonuniform case. Notice also that the definition we are going to give differs from the one given in [Reference Moraschini and Savini36, Reference Moraschini and Savini37] since ours relies on the differentiability of the slices of essentially bounded equivariant maps (see Definition 4.1). Moreover, the rigidity result we are going to obtain will refer to cocycles associated to lattices of
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
with image into
$\operatorname {\mathrm {{\rm G}}}(n)$
with image into
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
, with m possibly greater than or equal to n.
$\operatorname {\mathrm {{\rm G}}}(m)$
, with m possibly greater than or equal to n.
Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and fix
![]() $(X,\mu _X)$
a standard Borel probability
$(X,\mu _X)$
a standard Borel probability
![]() $\Gamma $
-space. Denote by
$\Gamma $
-space. Denote by
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the hyperbolic space over the division algebra
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the hyperbolic space over the division algebra
![]() $\operatorname {\mathrm {{\rm K}}}$
associated to
$\operatorname {\mathrm {{\rm K}}}$
associated to
![]() $\operatorname {\mathrm {{\rm G}}}(n)$
. Set
$\operatorname {\mathrm {{\rm G}}}(n)$
. Set
![]() $d=\dim _{\operatorname {\mathrm {\mathbb {R}}}}\operatorname {\mathrm {{\rm K}}}$
and assume
$d=\dim _{\operatorname {\mathrm {\mathbb {R}}}}\operatorname {\mathrm {{\rm K}}}$
and assume
![]() $d(n-1) \geq 2$
. Take
$d(n-1) \geq 2$
. Take
![]() $m \geq n$
and consider a measurable cocycle
$m \geq n$
and consider a measurable cocycle
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
which admits a measurable
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
which admits a measurable
![]() $\sigma $
-equivariant map
$\sigma $
-equivariant map
![]() $\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
whose slice
$\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
whose slice
![]() $\Phi _x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}, \hspace {5pt} \Phi _x(a):=\Phi (a,x)$
is differentiable, for almost every
$\Phi _x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}, \hspace {5pt} \Phi _x(a):=\Phi (a,x)$
is differentiable, for almost every
![]() $x \in X$
. This implies that we can consider the determinant associated to the pullback of the metric
$x \in X$
. This implies that we can consider the determinant associated to the pullback of the metric
![]() $g_m$
with respect to the slice
$g_m$
with respect to the slice
![]() $\Phi _x$
. More precisely, if we set
$\Phi _x$
. More precisely, if we set
![]() $p=d \cdot n$
, we can define the p-form
$p=d \cdot n$
, we can define the p-form
for almost every
![]() $x \in X$
, every
$x \in X$
, every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and every
![]() $u_1,\ldots ,u_p \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. In this way, we get a family
$u_1,\ldots ,u_p \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. In this way, we get a family
![]() $\{ \omega _x \}_{x \in X}$
of differential forms on
$\{ \omega _x \}_{x \in X}$
of differential forms on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. For almost every
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. For almost every
![]() $x \in X$
and every
$x \in X$
and every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, we can exploit the Riemannian structure on
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, we can exploit the Riemannian structure on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
to define the norm
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
to define the norm
where the set
![]() $\{ u_1,\ldots , u_p \}$
varies on the set of all the possible orthonormal frames of
$\{ u_1,\ldots , u_p \}$
varies on the set of all the possible orthonormal frames of
![]() $T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. We are going to say that
$T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. We are going to say that
![]() $\Phi $
is essentially bounded (or has essentially bounded slices) if there exists a real number
$\Phi $
is essentially bounded (or has essentially bounded slices) if there exists a real number
![]() $C>0$
such that
$C>0$
such that
for almost every
![]() $x \in X$
and every
$x \in X$
and every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Notice that this condition is not so restrictive, since, for instance, the natural map associated to a measurable cocycle satisfies this property (see Remark 4.2).
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Notice that this condition is not so restrictive, since, for instance, the natural map associated to a measurable cocycle satisfies this property (see Remark 4.2).
Assume now that
![]() $\Phi $
is essentially bounded. We are allowed to integrate with respect to the x-variable and, in this way, we get a well-defined differential form on
$\Phi $
is essentially bounded. We are allowed to integrate with respect to the x-variable and, in this way, we get a well-defined differential form on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
; that is,
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
; that is,
We claim that
![]() $\widetilde {\omega }_X$
is
$\widetilde {\omega }_X$
is
![]() $\Gamma $
-invariant – that is,
$\Gamma $
-invariant – that is,
![]() $\widetilde {\omega }_X \in \Omega ^p(\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})^\Gamma $
– and hence it induces a well-defined differential form
$\widetilde {\omega }_X \in \Omega ^p(\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})^\Gamma $
– and hence it induces a well-defined differential form
![]() $\omega _X \in \Omega ^p(\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})$
. More precisely, let
$\omega _X \in \Omega ^p(\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})$
. More precisely, let
![]() $\gamma \in \Gamma $
. We need to show that
$\gamma \in \Gamma $
. We need to show that
or, equivalently,
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
![]() $u_1,\ldots ,u_p \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. It holds that
$u_1,\ldots ,u_p \in T_a\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. It holds that
 $$ \begin{align*} \gamma^\ast \widetilde{\omega}_X(u_1,\ldots,u_p)&=\omega_X(D_a\gamma(u_1),\ldots,D_a\gamma(u_p))=\\ &=\int_X \omega_x(D_a\gamma (u_1),\ldots,D_a\gamma (u_p))d\mu_X(x)=\\ &=\int_X \omega_{\gamma y}(D_a\gamma (u_1),\ldots,D_a\gamma (u_p))d\mu_X(y) =(\bullet ) \ , \end{align*} $$
$$ \begin{align*} \gamma^\ast \widetilde{\omega}_X(u_1,\ldots,u_p)&=\omega_X(D_a\gamma(u_1),\ldots,D_a\gamma(u_p))=\\ &=\int_X \omega_x(D_a\gamma (u_1),\ldots,D_a\gamma (u_p))d\mu_X(x)=\\ &=\int_X \omega_{\gamma y}(D_a\gamma (u_1),\ldots,D_a\gamma (u_p))d\mu_X(y) =(\bullet ) \ , \end{align*} $$
where we set
![]() $x=\gamma y$
and we used the fact that
$x=\gamma y$
and we used the fact that
![]() $\Gamma $
acts on X via measure-preserving transformations. From the formula above we can argue
$\Gamma $
acts on X via measure-preserving transformations. From the formula above we can argue
 $$ \begin{align*} (\bullet)&=\int_X \sqrt{\det \left( \langle D_{\gamma a}\Phi_{\gamma y}(D_a\gamma(u_i)) ,D_{\gamma a}\Phi_{\gamma y}(D_a\gamma(u_j)) \rangle_m \right)}d\mu_X(y)=\\ &=\int_X \sqrt{\det \left( \langle D_{a}(\Phi_{\gamma y}\circ \gamma)(u_i)) ,D_{a}(\Phi_{\gamma y}\circ \gamma)(u_j)) \rangle_m \right)}d\mu_X(y)=\\ &=\int_X \sqrt{\det \left( \langle D_{a}(\sigma(\gamma,y)\Phi_y)(u_i)) ,D_{a}(\sigma(\gamma,y)\Phi_y)(u_j)) \rangle_m \right)}d\mu_X(y)=\\ &=\int_X \sqrt{\det \left( \langle D_{a}(\Phi_y)(u_i)) ,D_{a}(\Phi_y)(u_j)) \rangle_m \right)}d\mu_X(y)=\widetilde{\omega}_X(u_1,\ldots,u_p) , \end{align*} $$
$$ \begin{align*} (\bullet)&=\int_X \sqrt{\det \left( \langle D_{\gamma a}\Phi_{\gamma y}(D_a\gamma(u_i)) ,D_{\gamma a}\Phi_{\gamma y}(D_a\gamma(u_j)) \rangle_m \right)}d\mu_X(y)=\\ &=\int_X \sqrt{\det \left( \langle D_{a}(\Phi_{\gamma y}\circ \gamma)(u_i)) ,D_{a}(\Phi_{\gamma y}\circ \gamma)(u_j)) \rangle_m \right)}d\mu_X(y)=\\ &=\int_X \sqrt{\det \left( \langle D_{a}(\sigma(\gamma,y)\Phi_y)(u_i)) ,D_{a}(\sigma(\gamma,y)\Phi_y)(u_j)) \rangle_m \right)}d\mu_X(y)=\\ &=\int_X \sqrt{\det \left( \langle D_{a}(\Phi_y)(u_i)) ,D_{a}(\Phi_y)(u_j)) \rangle_m \right)}d\mu_X(y)=\widetilde{\omega}_X(u_1,\ldots,u_p) , \end{align*} $$
where we used the
![]() $\sigma $
-equivariance of
$\sigma $
-equivariance of
![]() $\Phi $
to pass from the second line to the third one and we exploited the fact that the cocycle
$\Phi $
to pass from the second line to the third one and we exploited the fact that the cocycle
![]() $\sigma $
takes value into the isometry group
$\sigma $
takes value into the isometry group
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
to conclude. Hence, we get that
$\operatorname {\mathrm {{\rm G}}}(m)$
to conclude. Hence, we get that
![]() $\widetilde {\omega }_X \in \Omega ^p(\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})^\Gamma $
and so we obtain a well-defined differential form
$\widetilde {\omega }_X \in \Omega ^p(\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})^\Gamma $
and so we obtain a well-defined differential form
![]() $\omega _X \in \Omega ^p(\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})$
.
$\omega _X \in \Omega ^p(\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}};\operatorname {\mathrm {\mathbb {R}}})$
.
Definition 4.1. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
and let
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
and let
![]() $(X,\mu _X)$
be a standard Borel probability
$(X,\mu _X)$
be a standard Borel probability
![]() $\Gamma $
-space. Let
$\Gamma $
-space. Let
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a measurable cocycle, with
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a measurable cocycle, with
![]() $m \geq n$
. Denote by
$m \geq n$
. Denote by
![]() $\mathscr {D}(\sigma )$
the set of essentially bounded
$\mathscr {D}(\sigma )$
the set of essentially bounded
![]() $\sigma $
-equivariant maps with differentiable slices. Given
$\sigma $
-equivariant maps with differentiable slices. Given
![]() $\Phi \in \mathscr {D}(\sigma )$
, we define the volume associated to the map
$\Phi \in \mathscr {D}(\sigma )$
, we define the volume associated to the map
![]() $\Phi $
as
$\Phi $
as
 $$ \begin{align*}\operatorname{\mathrm{{\rm Vol}}}(\Phi):=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \omega_X=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \omega_xd\mu_X(x)=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det(\Phi^\ast_x)g_m} d \mu_X(x) . \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{{\rm Vol}}}(\Phi):=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \omega_X=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \omega_xd\mu_X(x)=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det(\Phi^\ast_x)g_m} d \mu_X(x) . \end{align*} $$
Remark 4.2. Notice that when a measurable cocycle
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
admits a natural map
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
admits a natural map
![]() $F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
, the latter is an essentially bounded
$F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
, the latter is an essentially bounded
![]() $\sigma $
-equivariant map with differentiable slices. The essential boundedness comes from the estimate on that Jacobian of the slices of F. Indeed, the family of differential forms associated to F can be written as
$\sigma $
-equivariant map with differentiable slices. The essential boundedness comes from the estimate on that Jacobian of the slices of F. Indeed, the family of differential forms associated to F can be written as
where
![]() $\omega _n$
is the standard volume form on
$\omega _n$
is the standard volume form on
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. In particular, if we fix an orthonormal frame
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. In particular, if we fix an orthonormal frame
![]() $\{u_1,\ldots ,u_p\}$
of the tangent space
$\{u_1,\ldots ,u_p\}$
of the tangent space
![]() $T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, we have that
$T_a \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
, we have that
and this implies that F is essentially bounded. Hence, the set
![]() $\mathscr {D}(\sigma )$
of essentially bounded
$\mathscr {D}(\sigma )$
of essentially bounded
![]() $\sigma $
-equivariant map with differentiable slices is not empty, since it contains at least F.
$\sigma $
-equivariant map with differentiable slices is not empty, since it contains at least F.
The previous Remark allows us to define the notion of natural volume of a measurable cocycle.
Definition 4.3. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
and let
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
and let
![]() $(X,\mu _X)$
be a standard Borel probability
$(X,\mu _X)$
be a standard Borel probability
![]() $\Gamma $
-space. Let
$\Gamma $
-space. Let
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a measurable cocycle, with
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
be a measurable cocycle, with
![]() $m \geq n$
. Assume that
$m \geq n$
. Assume that
![]() $\sigma $
admits a natural map
$\sigma $
admits a natural map
![]() $F: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. The natural volume of the cocycle
$F: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. The natural volume of the cocycle
![]() $\sigma $
is defined as
$\sigma $
is defined as
Remark 4.4. This definition might seem quite strange to the reader who is confident with the work of Francaviglia and Klaff [Reference Francaviglia25, Reference Fisher, Morris and Whyte24]. If we wanted to follow their theoretical line we should have considered the infimum of the volumes over all possible elements of
![]() $\mathscr {D}(\sigma )$
. However, in that case, we would not be able to prove that the volume of the standard lattice embedding is maximal.
$\mathscr {D}(\sigma )$
. However, in that case, we would not be able to prove that the volume of the standard lattice embedding is maximal.
The first thing we want to show is that the notion of volume we gave is actually invariant along the
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class of a fixed measurable cocycle, analogous to what happens to the volume defined in [Reference Moraschini and Savini36].
$\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class of a fixed measurable cocycle, analogous to what happens to the volume defined in [Reference Moraschini and Savini36].
Proposition 4.5. Let
![]() $\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and let
$\Gamma \leq \operatorname {\mathrm {{\rm G}}}(n)$
be a torsion-free uniform lattice and let
![]() $(X,\mu _X)$
be a standard Borel probability
$(X,\mu _X)$
be a standard Borel probability
![]() $\Gamma $
-space. Consider
$\Gamma $
-space. Consider
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
a measurable cocycle which admits a natural map. Given any measurable map
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
a measurable cocycle which admits a natural map. Given any measurable map
![]() $f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, it holds that
$f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, it holds that
and hence the natural volume in constant along the
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class of
$\operatorname {\mathrm {{\rm G}}}(m)$
-cohomology class of
![]() $\sigma $
.
$\sigma $
.
Proof. Recall that
![]() $\mathscr {D}(\sigma )$
(respectively
$\mathscr {D}(\sigma )$
(respectively
![]() $\mathscr {D}(\sigma ^f)$
) is the set of all possible essentially bounded
$\mathscr {D}(\sigma ^f)$
) is the set of all possible essentially bounded
![]() $\sigma $
-equivariant (respectively
$\sigma $
-equivariant (respectively
![]() $\sigma ^f$
-equivariant) maps with differentiable slices. It is easy to verify that given
$\sigma ^f$
-equivariant) maps with differentiable slices. It is easy to verify that given
![]() $\Phi \in \mathscr {D}(\sigma )$
we can define
$\Phi \in \mathscr {D}(\sigma )$
we can define
and clearly
![]() $\Phi ^f \in \mathscr {D}(\sigma ^f)$
. In this way, we obtain a bijection
$\Phi ^f \in \mathscr {D}(\sigma ^f)$
. In this way, we obtain a bijection
We are going to prove that this bijection preserves the volume; that is,
![]() $\operatorname {\mathrm {\textrm {Vol}}}(\Phi )=\operatorname {\mathrm {\textrm {Vol}}}(\Phi ^f)$
for every
$\operatorname {\mathrm {\textrm {Vol}}}(\Phi )=\operatorname {\mathrm {\textrm {Vol}}}(\Phi ^f)$
for every
![]() $\Phi \in \mathscr {D}(\sigma )$
. Indeed, we have that
$\Phi \in \mathscr {D}(\sigma )$
. Indeed, we have that
 $$ \begin{align*} \operatorname{\mathrm{{\rm Vol}}}(\Phi^f)&=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det ( \Phi^f_x )^\ast g_m} d\mu_X(x)=\\ &=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det (f(x)^{-1}\Phi_x)^\ast g_m}d\mu_X(x)=\\ &=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det (\Phi_x)^\ast g_m}d\mu_X(x)=\operatorname{\mathrm{{\rm Vol}}}(\Phi) , \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{{\rm Vol}}}(\Phi^f)&=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det ( \Phi^f_x )^\ast g_m} d\mu_X(x)=\\ &=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det (f(x)^{-1}\Phi_x)^\ast g_m}d\mu_X(x)=\\ &=\int_{\Gamma \backslash \operatorname{\mathrm{\mathbb{H}^n_{{\rm K}}}}} \int_X \sqrt{\det (\Phi_x)^\ast g_m}d\mu_X(x)=\operatorname{\mathrm{{\rm Vol}}}(\Phi) , \end{align*} $$
where to pass from the second to the third line we used the fact that
![]() $f(x) \in \operatorname {\mathrm {{\rm G}}}(m)$
is an isometry for
$f(x) \in \operatorname {\mathrm {{\rm G}}}(m)$
is an isometry for
![]() $g_m$
.
$g_m$
.
If we now restrict our attention to the case of natural maps, we already proved in Proposition 3.4 that if F is the natural map associated to
![]() $\sigma $
, then
$\sigma $
, then
![]() $F^f$
is the one associated to
$F^f$
is the one associated to
![]() $\sigma ^f$
. From this consideration it follows that
$\sigma ^f$
. From this consideration it follows that
as desired.
After the study of the properties of the volume invariant of a given cocycle, we are now ready to prove our rigidity theorem; that is, Theorem 1.2.
Proof of Theorem 1.2. We are going to show first the Milnor–Wood type inequality. Define
![]() $M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Consider
$M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Consider
![]() $\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
and the associated set
$\sigma :\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
and the associated set
![]() $\mathscr {D}(\sigma )$
. As a consequence of Remark 4.2, we know that the natural map
$\mathscr {D}(\sigma )$
. As a consequence of Remark 4.2, we know that the natural map
![]() $F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
associated to
$F:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
associated to
![]() $\sigma $
is an element of
$\sigma $
is an element of
![]() $\mathscr {D}(\sigma )$
.
$\mathscr {D}(\sigma )$
.
By the estimate on the Jacobian of the slices of F, it follows that
 $$ \begin{align*} \operatorname{\mathrm{{\rm NV}}}(\sigma)&=\operatorname{\mathrm{{\rm Vol}}}(F)= \\ &= \int_{M} \int_X \sqrt{ \det F^\ast_x g_m }d\mu_X(x)=\\ &=\int_{M} \left(\int_X \operatorname{\mathrm{\textrm{Jac}}}_a F_x d\mu_X(x)\right) \omega_M \leq\\ &\leq \int_{M} \left(\int_X d\mu_X(x)\right) \omega_M=\operatorname{\mathrm{{\rm Vol}}}(M) , \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{{\rm NV}}}(\sigma)&=\operatorname{\mathrm{{\rm Vol}}}(F)= \\ &= \int_{M} \int_X \sqrt{ \det F^\ast_x g_m }d\mu_X(x)=\\ &=\int_{M} \left(\int_X \operatorname{\mathrm{\textrm{Jac}}}_a F_x d\mu_X(x)\right) \omega_M \leq\\ &\leq \int_{M} \left(\int_X d\mu_X(x)\right) \omega_M=\operatorname{\mathrm{{\rm Vol}}}(M) , \end{align*} $$
where
![]() $\omega _M$
is the volume form associated to the standard Riemannian metric on M. In this way, we get our desired inequality.
$\omega _M$
is the volume form associated to the standard Riemannian metric on M. In this way, we get our desired inequality.
We now prove the rigidity statement. We first introduce some notation. Denote by
 $$ \begin{align*}i_{n,m}:\operatorname{\mathrm{\textrm{G}}}(n) \rightarrow \operatorname{\mathrm{\textrm{G}}}(m), \hspace{5pt} g \mapsto \left( \begin{array}{cc} g & 0 \\ 0 & \operatorname{\mathrm{\textrm{I}}}_{m-n}\\ \end{array} \right) , \end{align*} $$
$$ \begin{align*}i_{n,m}:\operatorname{\mathrm{\textrm{G}}}(n) \rightarrow \operatorname{\mathrm{\textrm{G}}}(m), \hspace{5pt} g \mapsto \left( \begin{array}{cc} g & 0 \\ 0 & \operatorname{\mathrm{\textrm{I}}}_{m-n}\\ \end{array} \right) , \end{align*} $$
the upper-left corner embedding. Here
![]() $\operatorname {\mathrm {\textrm {I}}}_{m-n}$
stands for the identity matrix of order
$\operatorname {\mathrm {\textrm {I}}}_{m-n}$
stands for the identity matrix of order
![]() $(m-n)$
. Let
$(m-n)$
. Let
![]() $\jmath _{n,m}:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
be the totally geodesic embedding of
$\jmath _{n,m}:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
be the totally geodesic embedding of
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
into
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
into
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
which is
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
which is
![]() $i_{n,m}$
-equivariant.
$i_{n,m}$
-equivariant.
Assume now that
![]() $\operatorname {\mathrm {\textrm {NV}}}(\sigma )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
. By definition it follows that
$\operatorname {\mathrm {\textrm {NV}}}(\sigma )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
. By definition it follows that
where F still denotes the natural map associated to
![]() $\sigma $
. By writing explicitly the equality above we get
$\sigma $
. By writing explicitly the equality above we get
 $$ \begin{align} \operatorname{\mathrm{{\rm Vol}}}(M) = \int_{M} \int_X \sqrt{ \det F^\ast_x g_m }d\mu_X(x) = \int_{M} \left(\int_X \operatorname{\mathrm{\textrm{Jac}}}_a F_x d\mu_X(x)\right) \omega_M . \end{align} $$
$$ \begin{align} \operatorname{\mathrm{{\rm Vol}}}(M) = \int_{M} \int_X \sqrt{ \det F^\ast_x g_m }d\mu_X(x) = \int_{M} \left(\int_X \operatorname{\mathrm{\textrm{Jac}}}_a F_x d\mu_X(x)\right) \omega_M . \end{align} $$
Since
![]() $\operatorname {\mathrm {\textrm {Jac}}}_a F_x \leq 1$
for every
$\operatorname {\mathrm {\textrm {Jac}}}_a F_x \leq 1$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
![]() $x \in X$
, Equation (11) implies that
$x \in X$
, Equation (11) implies that
for almost every point of the
![]() $\Gamma $
-fundamental domain in
$\Gamma $
-fundamental domain in
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and for almost every
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and for almost every
![]() $x \in X$
. By the
$x \in X$
. By the
![]() $\sigma $
-equivariance of F, we have that
$\sigma $
-equivariance of F, we have that
for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
![]() $x \in X$
. Now fix
$x \in X$
. Now fix
![]() $x \in X$
and consider the slice
$x \in X$
and consider the slice
![]() $F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
for which it holds
$F_x:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
for which it holds
![]() $\operatorname {\mathrm {\textrm {Jac}}}_aF_x=1$
for almost every
$\operatorname {\mathrm {\textrm {Jac}}}_aF_x=1$
for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. By [Reference Besson, Courtois and Gallot6, Reference Francaviglia25] it follows that
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. By [Reference Besson, Courtois and Gallot6, Reference Francaviglia25] it follows that
![]() $F_x$
coincides essentially with a totally geodesic embedding of
$F_x$
coincides essentially with a totally geodesic embedding of
![]() $\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
into
$\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
into
![]() $\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. More precisely, there must exist
$\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. More precisely, there must exist
![]() $f(x) \in \operatorname {\mathrm {{\rm G}}}(m)$
such that
$f(x) \in \operatorname {\mathrm {{\rm G}}}(m)$
such that
for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(actually every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
(actually every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
by the differentiability of the slices). In this way, we obtain a map
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
by the differentiability of the slices). In this way, we obtain a map
![]() $f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
. Since by assumption X is a standard Borel space, the function
$f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
. Since by assumption X is a standard Borel space, the function
![]() $\widehat {F}:X \rightarrow \textrm {Meas}(\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}},\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}), \ \widehat {F}(x):=F_x$
is measurable by [Reference Feldman and Moore22, Lemma 2.6], and this implies the measurability of f. In this way, we get a measurable map
$\widehat {F}:X \rightarrow \textrm {Meas}(\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}},\operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}), \ \widehat {F}(x):=F_x$
is measurable by [Reference Feldman and Moore22, Lemma 2.6], and this implies the measurability of f. In this way, we get a measurable map
![]() $f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
which conjugates F to the totally geodesic embedding
$f:X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
which conjugates F to the totally geodesic embedding
![]() $\jmath _{n,m}$
. Following the same strategy exposed in [Reference Bucher, Burger and Iozzi4, Proposition 3.2], we claim that
$\jmath _{n,m}$
. Following the same strategy exposed in [Reference Bucher, Burger and Iozzi4, Proposition 3.2], we claim that
![]() $\sigma $
is cohomologous to the restriction
$\sigma $
is cohomologous to the restriction
![]() $i_{n,m}|_{\Gamma }$
of the upper-left corner embedding to the lattice
$i_{n,m}|_{\Gamma }$
of the upper-left corner embedding to the lattice
![]() $\Gamma $
, modulo possibly a compact subgroup.
$\Gamma $
, modulo possibly a compact subgroup.
Let
be the subgroup of
![]() $\operatorname {\mathrm {{\rm G}}}(m)$
fixing pointwise the image of
$\operatorname {\mathrm {{\rm G}}}(m)$
fixing pointwise the image of
![]() $\jmath _{n,m}$
. This is the trivial group when
$\jmath _{n,m}$
. This is the trivial group when
![]() $n=m$
and it is compact when
$n=m$
and it is compact when
![]() $m>n$
. Fix
$m>n$
. Fix
![]() $\gamma \in \Gamma $
. For almost every
$\gamma \in \Gamma $
. For almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}},x \in X$
, on one hand it holds that
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}},x \in X$
, on one hand it holds that
and on the other hand we have
Hence, it follows that
and the claim is proved.
In contrast, consider the cocycle
![]() $\sigma _{i_{n,m}}:\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
associated to the representation
$\sigma _{i_{n,m}}:\Gamma \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
associated to the representation
![]() $i_{n,m}$
restricted to
$i_{n,m}$
restricted to
![]() $\Gamma $
. It is easy to verify that the natural map associated to this cocycle is given by
$\Gamma $
. It is easy to verify that the natural map associated to this cocycle is given by
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and almost every
![]() $x \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. We have that
$x \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. We have that
 $$ \begin{align*} \operatorname{\mathrm{{\rm NV}}}(\sigma_{i_{n,m}})&=\operatorname{\mathrm{{\rm Vol}}}(F)=\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_aF_x d\mu_X(x) \right)\omega_M=\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a \jmath_{n,m} d\mu_X(x) \right) \omega_M=\\ &=\int_{M} \operatorname{\mathrm{\textrm{Jac}}}_a \jmath_{n,m} \omega_M=\int_M \omega_M=\operatorname{\mathrm{{\rm Vol}}}(M) , \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{{\rm NV}}}(\sigma_{i_{n,m}})&=\operatorname{\mathrm{{\rm Vol}}}(F)=\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_aF_x d\mu_X(x) \right)\omega_M=\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a \jmath_{n,m} d\mu_X(x) \right) \omega_M=\\ &=\int_{M} \operatorname{\mathrm{\textrm{Jac}}}_a \jmath_{n,m} \omega_M=\int_M \omega_M=\operatorname{\mathrm{{\rm Vol}}}(M) , \end{align*} $$
and the statement follows.□
It is worth noticing that all of the results we have shown so far are still valid for nonuniform lattice, since we did not exploit the property of being uniform for the lattice
![]() $\Gamma $
.
$\Gamma $
.
We conclude the section by underling that importance of the previous theorem, since in the particular case when
![]() $n=m$
, it has been exploited by the author [Reference Savini48] to prove the
$n=m$
, it has been exploited by the author [Reference Savini48] to prove the
![]() $1$
-tautness of the group
$1$
-tautness of the group
![]() $\operatorname {\mathrm {{\rm PU}}}(n,1)$
, when
$\operatorname {\mathrm {{\rm PU}}}(n,1)$
, when
![]() $n \geq 2$
.
$n \geq 2$
.
5 Volume of equivariant maps and mapping degree
In this section we are going to show a suitable adaptation of the mapping degree theorem to the context of measurable cocycles associated to uniform lattices of rank-1 Lie groups (see also [Reference Douady and Earle18, Proposition 3.1]). We will introduce the notion of pullback of a measurable cocycle
![]() $\sigma $
with respect to a continuous map between closed manifolds. Since the same can be done for a measurable
$\sigma $
with respect to a continuous map between closed manifolds. Since the same can be done for a measurable
![]() $\sigma $
-equivariant map
$\sigma $
-equivariant map
![]() $\Phi $
with essentially bounded differentiable slices, we are going to show that the volume of the pullback
$\Phi $
with essentially bounded differentiable slices, we are going to show that the volume of the pullback
![]() $f^\ast \Phi $
bounds from above the volume of
$f^\ast \Phi $
bounds from above the volume of
![]() $\Phi $
multiplied by the mapping degree of the continuous map.
$\Phi $
multiplied by the mapping degree of the continuous map.
Let
![]() $\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Denote by
$\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Denote by
![]() $M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
$M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and
![]() $N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the closed hyperbolic manifolds associated to
$N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
the closed hyperbolic manifolds associated to
![]() $\Gamma $
and
$\Gamma $
and
![]() $\Lambda $
, respectively. Consider a continuous map
$\Lambda $
, respectively. Consider a continuous map
![]() $f:M \rightarrow N$
and denote by
$f:M \rightarrow N$
and denote by
![]() $\pi _1(f):\Gamma \rightarrow \Lambda $
the homomorphism induced on the fundamental groups. Let
$\pi _1(f):\Gamma \rightarrow \Lambda $
the homomorphism induced on the fundamental groups. Let
![]() $(X,\mu _X)$
be a standard Borel probability
$(X,\mu _X)$
be a standard Borel probability
![]() $\Lambda $
-space. Following [Reference Moraschini and Savini36, Section 6], given a measurable cocycle
$\Lambda $
-space. Following [Reference Moraschini and Savini36, Section 6], given a measurable cocycle
![]() $\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, we define the pullback cocycle of
$\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
, we define the pullback cocycle of
![]() $\sigma $
with respect to f as follows:
$\sigma $
with respect to f as follows:
Here
![]() $(X,\mu _X)$
is viewed as a
$(X,\mu _X)$
is viewed as a
![]() $\Gamma $
-space with the action induced by the map
$\Gamma $
-space with the action induced by the map
![]() $\pi _1(f)$
. As shown in [Reference Moraschini and Savini36, Lemma 6.1] the map
$\pi _1(f)$
. As shown in [Reference Moraschini and Savini36, Lemma 6.1] the map
![]() $f^\ast \sigma $
is a well-defined cocycle.
$f^\ast \sigma $
is a well-defined cocycle.
Given a continuous map
![]() $f:M \rightarrow N$
with nonzero degree, it is well-known by [Reference Boland and Newberger14, Reference Fisher, Morris and Whyte24] that there exists an essentially unique measurable map
$f:M \rightarrow N$
with nonzero degree, it is well-known by [Reference Boland and Newberger14, Reference Fisher, Morris and Whyte24] that there exists an essentially unique measurable map
![]() $\varphi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which is
$\varphi :\partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \partial _\infty \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which is
![]() $\pi _1(f)$
-equivariant. Hence, by following the approach of [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] there exists a natural map
$\pi _1(f)$
-equivariant. Hence, by following the approach of [Reference Besson, Courtois and Gallot6, Reference Besson, Courtois and Gallot7, Reference Besson, Courtois and Gallot8] there exists a natural map
![]() $\widetilde {F}:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which is smooth and
$\widetilde {F}:\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
which is smooth and
![]() $\pi _1(f)$
-equivariant. This map descends to a smooth map
$\pi _1(f)$
-equivariant. This map descends to a smooth map
![]() $F:M \rightarrow N$
which has the same degree of f. Additionally, we recall the standard bound on the Jacobian of
$F:M \rightarrow N$
which has the same degree of f. Additionally, we recall the standard bound on the Jacobian of
![]() $\widetilde {F}$
; that is,
$\widetilde {F}$
; that is,
![]() $\operatorname {\mathrm {\textrm {Jac}}}_a \widetilde {F} \leq 1$
for every
$\operatorname {\mathrm {\textrm {Jac}}}_a \widetilde {F} \leq 1$
for every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
.
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
.
Now consider a measurable
![]() $\sigma $
-equivariant map
$\sigma $
-equivariant map
![]() $\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. We can define the pullback of the map
$\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
. We can define the pullback of the map
![]() $\Phi $
along the continuous map f as follows:
$\Phi $
along the continuous map f as follows:
where
![]() $\widetilde {F}$
is the lift of the natural map previously described. Having introduced all the notation we need, we are now ready to prove our version of mapping degree theorem.
$\widetilde {F}$
is the lift of the natural map previously described. Having introduced all the notation we need, we are now ready to prove our version of mapping degree theorem.
Proof of Proposition 1.3. Up to changing the orientation to either M or N we can suppose that the degree of the map
![]() $f:M \rightarrow N$
is positive. Denote by
$f:M \rightarrow N$
is positive. Denote by
![]() $\omega _M$
and
$\omega _M$
and
![]() $\omega _N$
the volume forms induced on M and on N by the standard hyperbolic metric, respectively.
$\omega _N$
the volume forms induced on M and on N by the standard hyperbolic metric, respectively.
Let now
![]() $\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
be the equivariant map we have in statement. The following chain of equalities holds:
$\Phi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
be the equivariant map we have in statement. The following chain of equalities holds:
 $$ \begin{align*} \operatorname{\mathrm{{\rm Vol}}}(f^\ast \Phi)&=\int_{M} \int_X \sqrt{ \det (f^\ast \Phi)_x^\ast g_m } d\mu_X(x)=\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a(f^\ast \Phi)_x d\mu_X(x)\right) \omega_M =\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a(\Phi_x \circ \widetilde{F})d\mu_X(x) \right) \omega_M . \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{{\rm Vol}}}(f^\ast \Phi)&=\int_{M} \int_X \sqrt{ \det (f^\ast \Phi)_x^\ast g_m } d\mu_X(x)=\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a(f^\ast \Phi)_x d\mu_X(x)\right) \omega_M =\\ &=\int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a(\Phi_x \circ \widetilde{F})d\mu_X(x) \right) \omega_M . \end{align*} $$
We can now take out from the sign of integration along X the Jacobian of the map
![]() $\widetilde {F}$
(actually of the map F by its equivariance property):
$\widetilde {F}$
(actually of the map F by its equivariance property):
 $$ \begin{align*} \int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a(\Phi_x \circ \widetilde{F})d\mu_X(x) \right) \omega_M&=\int_{M} \operatorname{\mathrm{\textrm{Jac}}}_a F \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_{\widetilde{F}(a)} \Phi_x d\mu_X(x) \right) \omega_M = \\ &=\int_{N} \sum_{a \in F^{-1}(b)}\left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_b \Phi_x d\mu_X(x) \right) \omega_N =\\ &= \int_{N} \operatorname{\mathrm{\mathcal{N}}}(b) \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_b \Phi_x d\mu_X(x) \right) \omega_N \geq \\ &\geq \int_{N} \deg(F) \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_b \Phi_x d\mu_X(x) \right) \omega_N\\ &= \deg(f) \cdot \operatorname{\mathrm{{\rm Vol}}}(\Phi) . \end{align*} $$
$$ \begin{align*} \int_{M} \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_a(\Phi_x \circ \widetilde{F})d\mu_X(x) \right) \omega_M&=\int_{M} \operatorname{\mathrm{\textrm{Jac}}}_a F \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_{\widetilde{F}(a)} \Phi_x d\mu_X(x) \right) \omega_M = \\ &=\int_{N} \sum_{a \in F^{-1}(b)}\left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_b \Phi_x d\mu_X(x) \right) \omega_N =\\ &= \int_{N} \operatorname{\mathrm{\mathcal{N}}}(b) \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_b \Phi_x d\mu_X(x) \right) \omega_N \geq \\ &\geq \int_{N} \deg(F) \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_b \Phi_x d\mu_X(x) \right) \omega_N\\ &= \deg(f) \cdot \operatorname{\mathrm{{\rm Vol}}}(\Phi) . \end{align*} $$
In the computation above, for any
![]() $b \in N$
we defined the number
$b \in N$
we defined the number
![]() $\operatorname {\mathrm {\mathcal {N}}}(b)$
as the cardinality
$\operatorname {\mathrm {\mathcal {N}}}(b)$
as the cardinality
and we used the co-area formula to move from the first line to the second one. Since
![]() $\operatorname {\mathrm {\mathcal {N}}}(b) \geq \deg (F)$
and F has the same degree of f, the desired inequality follows.
$\operatorname {\mathrm {\mathcal {N}}}(b) \geq \deg (F)$
and F has the same degree of f, the desired inequality follows.
Suppose now that f is homotopic to a local isometry. By the strict version of mapping degree theorem (see [Reference Thurston50, Theorem 6.4] for the real hyperbolic case and [Reference Besson, Courtois and Gallot6, Théorèm Principal] for the rank-1 case), it follows that
since F and f have the same degree. We claim that this implies that
![]() $F:M \rightarrow N$
is a local isometry. Indeed, following the same reasoning exposed in [Reference Besson, Courtois and Gallot6, Appendix C], we have that
$F:M \rightarrow N$
is a local isometry. Indeed, following the same reasoning exposed in [Reference Besson, Courtois and Gallot6, Appendix C], we have that
In our particular case, all of the inequalities above are actually equalities and hence
![]() $\operatorname {\mathrm {\mathcal {N}}}(b)=\deg (F)$
and, by the equivariance of
$\operatorname {\mathrm {\mathcal {N}}}(b)=\deg (F)$
and, by the equivariance of
![]() $\widetilde {F}$
, we obtain
$\widetilde {F}$
, we obtain
![]() $\operatorname {\mathrm {\textrm {Jac}}}_a \widetilde {F}=1$
for almost every
$\operatorname {\mathrm {\textrm {Jac}}}_a \widetilde {F}=1$
for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. This means that
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. This means that
![]() $\widetilde {F}: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
coincides essentially with an isometry (hence it is an isometry being differentiable). Thus, the induced map
$\widetilde {F}: \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \rightarrow \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
coincides essentially with an isometry (hence it is an isometry being differentiable). Thus, the induced map
![]() $F:M \rightarrow N$
is a local isometry.
$F:M \rightarrow N$
is a local isometry.
By the conditions on both the cardinality
![]() $\operatorname {\mathrm {\mathcal {N}}}(b)$
and on the Jacobian of F, if we substitute their respective values into the chain of equalities at the beginning of the proof, we get that
$\operatorname {\mathrm {\mathcal {N}}}(b)$
and on the Jacobian of F, if we substitute their respective values into the chain of equalities at the beginning of the proof, we get that
as claimed.□
We would like to apply the proposition above to argue a relation between the degree of the continuous map f and the natural volumes of the cocycles
![]() $\sigma $
and
$\sigma $
and
![]() $f^\ast \sigma $
, respectively. Unfortunately, if
$f^\ast \sigma $
, respectively. Unfortunately, if
![]() $\Psi $
is the natural map associated to
$\Psi $
is the natural map associated to
![]() $\sigma $
, it is not true a priori that
$\sigma $
, it is not true a priori that
![]() $f^\ast \Psi $
is the natural map associated to
$f^\ast \Psi $
is the natural map associated to
![]() $f^\ast \sigma $
. For this reason, a weaker statement is given by the following.
$f^\ast \sigma $
. For this reason, a weaker statement is given by the following.
Corollary 5.1. Let
![]() $\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Set
$\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Set
![]() $M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
,
$M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
,
![]() $N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and let
$N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and let
![]() $f:M \rightarrow N$
be a continuous map with nonvanishing degree. Fix a standard Borel probability
$f:M \rightarrow N$
be a continuous map with nonvanishing degree. Fix a standard Borel probability
![]() $\Lambda $
-space
$\Lambda $
-space
![]() $(X,\mu _X)$
and consider a measurable cocycle
$(X,\mu _X)$
and consider a measurable cocycle
![]() $\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
. Suppose that
$\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
. Suppose that
![]() $\sigma $
admits a natural map
$\sigma $
admits a natural map
![]() $\Psi $
. Then it holds that
$\Psi $
. Then it holds that
 $$ \begin{align*}|\deg(f)| \leq \frac{\operatorname{\mathrm{{\rm Vol}}}(f^\ast\Psi)}{\operatorname{\mathrm{{\rm NV}}}(\sigma)} . \end{align*} $$
$$ \begin{align*}|\deg(f)| \leq \frac{\operatorname{\mathrm{{\rm Vol}}}(f^\ast\Psi)}{\operatorname{\mathrm{{\rm NV}}}(\sigma)} . \end{align*} $$
Additionally, if f is homotopic to a local isometry, then the equality is attained.
Proof. The claim follows immediately by substituting
![]() $\Psi $
in Proposition 1.3 and noticing that we have
$\Psi $
in Proposition 1.3 and noticing that we have
![]() $\operatorname {\mathrm {\textrm {NV}}}(\sigma )=\operatorname {\mathrm {\textrm {Vol}}}(\Psi )$
by definition.
$\operatorname {\mathrm {\textrm {NV}}}(\sigma )=\operatorname {\mathrm {\textrm {Vol}}}(\Psi )$
by definition.
Remark 5.2. In the situation of Corollary 5.1, it is worth noticing that
![]() $\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )$
is bounded from above by
$\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )$
is bounded from above by
![]() $\operatorname {\mathrm {\textrm {Vol}}}(M)$
. Indeed, we have that
$\operatorname {\mathrm {\textrm {Vol}}}(M)$
. Indeed, we have that
 $$ \begin{align} \operatorname{\mathrm{{\rm Vol}}}(f^\ast \Psi) &= \int_M \operatorname{\mathrm{\textrm{Jac}}}_a F \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_{\widetilde{F}(a)}\Psi_x d\mu_X(x) \right) \omega_M \leq \nonumber\\ &\leq \int_M \left( \int_X d\mu_X(x) \right) \omega_M =\operatorname{\mathrm{{\rm Vol}}}(M) , \end{align} $$
$$ \begin{align} \operatorname{\mathrm{{\rm Vol}}}(f^\ast \Psi) &= \int_M \operatorname{\mathrm{\textrm{Jac}}}_a F \left( \int_X \operatorname{\mathrm{\textrm{Jac}}}_{\widetilde{F}(a)}\Psi_x d\mu_X(x) \right) \omega_M \leq \nonumber\\ &\leq \int_M \left( \int_X d\mu_X(x) \right) \omega_M =\operatorname{\mathrm{{\rm Vol}}}(M) , \end{align} $$
where we moved from the first line to the second one using the bound on the Jacobian of both natural maps
![]() $\widetilde F$
and
$\widetilde F$
and
![]() $\Psi $
.
$\Psi $
.
We conclude this section by giving a characterisation of continuous maps homotopic to local isometries in terms of naturally maximal cocycles. A cocycle
![]() $\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
is naturally maximal if it admits a natural map
$\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
is naturally maximal if it admits a natural map
![]() $\Psi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
and it holds that
$\Psi :\operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}} \times X \rightarrow \operatorname {\mathrm {\mathbb {H}^m_{{\rm K}}}}$
and it holds that
Compare the following result with [Reference Moraschini and Savini36, Proposition 1.4].
Corollary 5.3. Let
![]() $\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Set
$\Gamma ,\Lambda \leq \operatorname {\mathrm {{\rm G}}}(n)$
be two torsion-free uniform lattices. Set
![]() $M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
,
$M=\Gamma \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
,
![]() $N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and let
$N=\Lambda \backslash \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
and let
![]() $f:M \rightarrow N$
be a continuous map with nonvanishing degree. Fix a standard Borel probability
$f:M \rightarrow N$
be a continuous map with nonvanishing degree. Fix a standard Borel probability
![]() $\Lambda $
-space
$\Lambda $
-space
![]() $(X,\mu _X)$
and consider a naturally maximal cocycle
$(X,\mu _X)$
and consider a naturally maximal cocycle
![]() $\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
with natural map
$\sigma :\Lambda \times X \rightarrow \operatorname {\mathrm {{\rm G}}}(m)$
with natural map
![]() $\Psi $
. Then f is homotopic to a local isometry if and only if
$\Psi $
. Then f is homotopic to a local isometry if and only if
![]() $\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
.
$\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
.
Proof. We are going to keep the same notation of both Proposition 1.3 and Corollary 5.1. Suppose that f is homotopic to a local isometry. By Corollary 5.1 it follows that
and the latter equality is justified by the maximality assumption. As a consequence of the strict version of mapping degree theorem [Reference Thurston50, Theorem 6.4], [Reference Besson, Courtois and Gallot6, Théorèm Principal], it holds that
and hence
![]() $\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
, as claimed.
$\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
, as claimed.
Assume now that
![]() $\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
. By Inequality (12) we argue that
$\operatorname {\mathrm {\textrm {Vol}}}(f^\ast \Psi )=\operatorname {\mathrm {\textrm {Vol}}}(M)$
. By Inequality (12) we argue that
for almost every
![]() $a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Thus,
$a \in \operatorname {\mathrm {\mathbb {H}^n_{{\rm K}}}}$
. Thus,
![]() $\widetilde F$
is an isometry and
$\widetilde F$
is an isometry and
![]() $F:M \rightarrow N$
is a local isometry. In particular, it holds that
$F:M \rightarrow N$
is a local isometry. In particular, it holds that
and the statement follows again by the strict version of that mapping degree theorem.
Acknowledgements
I am grateful to the anonymous referee for her/his suggestions that allowed me to improve the quality of the article.
Competing Interest
None.