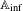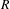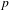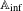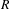Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kedlaya, Kiran S.
2020.
p-adic Hodge Theory.
p.
129.
Morrow, Matthew
2020.
p-adic Hodge Theory.
p.
1.
Kedlaya, Kiran S.
2022.
Perfectoid Spaces.
p.
221.
Anschütz, Johannes
2022.
Extending torsors on the punctured Spec(A
inf).
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 783,
p.
227.