Published online by Cambridge University Press: 12 March 2019
Let 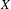 $X$ be a normal complex projective variety,
$X$ be a normal complex projective variety, 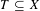 $T\subseteq X$ a subvariety of dimension
$T\subseteq X$ a subvariety of dimension  $m$ (possibly
$m$ (possibly  $T=X$) and
$T=X$) and 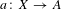 $a:X\rightarrow A$ a morphism to an abelian variety such that
$a:X\rightarrow A$ a morphism to an abelian variety such that  $\text{Pic}^{0}(A)$ injects into
$\text{Pic}^{0}(A)$ injects into  $\text{Pic}^{0}(T)$; let
$\text{Pic}^{0}(T)$; let  $L$ be a line bundle on
$L$ be a line bundle on 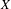 $X$ and
$X$ and 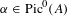 $\unicode[STIX]{x1D6FC}\in \text{Pic}^{0}(A)$ a general element.
$\unicode[STIX]{x1D6FC}\in \text{Pic}^{0}(A)$ a general element.
We introduce two new ingredients for the study of linear systems on 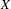 $X$. First of all, we show the existence of a factorization of the map
$X$. First of all, we show the existence of a factorization of the map  $a$, called the eventual map of
$a$, called the eventual map of  $L$ on
$L$ on  $T$, which controls the behavior of the linear systems
$T$, which controls the behavior of the linear systems 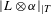 $|L\otimes \unicode[STIX]{x1D6FC}|_{|T}$, asymptotically with respect to the pullbacks to the connected étale covers
$|L\otimes \unicode[STIX]{x1D6FC}|_{|T}$, asymptotically with respect to the pullbacks to the connected étale covers 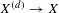 $X^{(d)}\rightarrow X$ induced by the
$X^{(d)}\rightarrow X$ induced by the 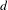 $d$-th multiplication map of
$d$-th multiplication map of  $A$.
$A$.
Second, we define the so-called continuous rank function $x\mapsto h_{a}^{0}(X_{|T},L+xM)$, where
$x\mapsto h_{a}^{0}(X_{|T},L+xM)$, where 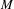 $M$ is the pullback of an ample divisor of
$M$ is the pullback of an ample divisor of  $A$. This function extends to a continuous function of
$A$. This function extends to a continuous function of 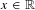 $x\in \mathbb{R}$, which is differentiable except possibly at countably many points; when
$x\in \mathbb{R}$, which is differentiable except possibly at countably many points; when 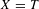 $X=T$ we compute the left derivative explicitly.
$X=T$ we compute the left derivative explicitly.
As an application, we give quick short proofs of a wide range of new Clifford–Severi inequalities, i.e., geographical bounds of the form 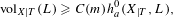 $$\begin{eqnarray}\displaystyle \text{vol}_{X|T}(L)\geqslant C(m)h_{a}^{0}(X_{|T},L), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{vol}_{X|T}(L)\geqslant C(m)h_{a}^{0}(X_{|T},L), & & \displaystyle \nonumber\end{eqnarray}$$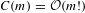 $C(m)={\mathcal{O}}(m!)$ depends on several geometrical properties of
$C(m)={\mathcal{O}}(m!)$ depends on several geometrical properties of 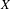 $X$,
$X$,  $L$ or
$L$ or  $a$.
$a$.
The first author was supported by MINECO MTM2015-69135-P “Geometría y Topología de Variedades, Álgebra y Aplicaciones” and by Generalitat de Catalunya SGR2014-634. The second and third authors are members of G.N.S.A.G.A.–I.N.d.A.M. This research was partially supported by MIUR (Italy) through PRIN 2010–11 “Geometria delle varietà algebriche” and PRIN 2012–13 “Moduli, strutture geometriche e loro applicazioni”.