Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Han, Jingjun
Liu, Yuchen
and
Qi, Lu
2022.
ACC for local volumes and boundedness of singularities.
Journal of Algebraic Geometry,
Vol. 32,
Issue. 3,
p.
519.
Liu, Yuchen
2022.
K-stability of cubic fourfolds.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 786,
p.
55.
Ascher, Kenneth
DeVleming, Kristin
and
Liu, Yuchen
2023.
K-stability and birational models of moduli of quartic K3 surfaces.
Inventiones mathematicae,
Vol. 232,
Issue. 2,
p.
471.
Zhou, Chuyu
2024.
On the Shape of the K-semistable Domain and Wall Crossing for K-stability.
Peking Mathematical Journal,
Dervan, Ruadhaí
and
Papazachariou, Theodoros Stylianos
2024.
On divisorial stability of finite covers.
Forum of Mathematics, Sigma,
Vol. 12,
Issue. ,
Zhao, Junyan
2024.
Compactifications of moduli of del Pezzo surfaces via line arrangement and K-stability.
Canadian Journal of Mathematics,
Vol. 76,
Issue. 6,
p.
2115.
Zhao, Junyan
2024.
Moduli of genus six curves and K-stability.
Transactions of the American Mathematical Society, Series B,
Vol. 11,
Issue. 26,
p.
863.
Ascher, Kenneth
DeVleming, Kristin
and
Liu, Yuchen
2024.
Wall crossing for K‐moduli spaces of plane curves.
Proceedings of the London Mathematical Society,
Vol. 128,
Issue. 6,
Liu, Yuchen
and
Zhao, Junyan
2025.
K-moduli of Fano threefolds and genus four curves.
Journal für die reine und angewandte Mathematik (Crelles Journal),
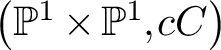 $\left(\mathbb {P}^1\times \mathbb {P}^1, cC\right)$
, where C is a
$\left(\mathbb {P}^1\times \mathbb {P}^1, cC\right)$
, where C is a
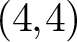 $(4,4)$
curve and their wall crossings coincide with the VGIT quotients of
$(4,4)$
curve and their wall crossings coincide with the VGIT quotients of
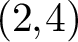 $(2,4)$
, complete intersection curves in
$(2,4)$
, complete intersection curves in
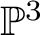 $\mathbb {P}^3$
. This, together with recent results by Laza and O’Grady, implies that these K-moduli spaces form a natural interpolation between the GIT moduli space of
$\mathbb {P}^3$
. This, together with recent results by Laza and O’Grady, implies that these K-moduli spaces form a natural interpolation between the GIT moduli space of
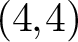 $(4,4)$
curves on
$(4,4)$
curves on
 $\mathbb {P}^1\times \mathbb {P}^1$
and the Baily–Borel compactification of moduli of quartic hyperelliptic K3 surfaces.
$\mathbb {P}^1\times \mathbb {P}^1$
and the Baily–Borel compactification of moduli of quartic hyperelliptic K3 surfaces.