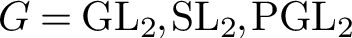1 Introduction
Let C be a compact Riemann surface of genus
![]() $g \geq 2$
and G be a complex reductive algebraic group. The G-character variety of C, or Betti moduli space, is the affine GIT quotient
$g \geq 2$
and G be a complex reductive algebraic group. The G-character variety of C, or Betti moduli space, is the affine GIT quotient

It parametrises isomorphism classes of semi-simple representations of the fundamental group of C with value in G. Remarkably, the space
![]() ${M}_{\mathrm {B}}(C,G)$
is homeomorphic to the Dolbeault moduli space
${M}_{\mathrm {B}}(C,G)$
is homeomorphic to the Dolbeault moduli space
![]() ${M}_{\mathrm {Dol}}(C,G)$
, parametrising instead isomorphism classes of semistable principal G-Higgs bundles on C of degree zero; see [Reference Simpson66]. For example, a
${M}_{\mathrm {Dol}}(C,G)$
, parametrising instead isomorphism classes of semistable principal G-Higgs bundles on C of degree zero; see [Reference Simpson66]. For example, a
![]() $\operatorname {GL}_n$
-Higgs bundle is a pair
$\operatorname {GL}_n$
-Higgs bundle is a pair
![]() $(E, \phi )$
with E vector bundle of rank n and
$(E, \phi )$
with E vector bundle of rank n and
![]() $\phi \in H^0(C, \operatorname {End}(E)\otimes K)$
. Such a pair is an
$\phi \in H^0(C, \operatorname {End}(E)\otimes K)$
. Such a pair is an
![]() $\operatorname {SL}_n$
-Higgs bundle if in addition the determinant of E is trivial and the trace of
$\operatorname {SL}_n$
-Higgs bundle if in addition the determinant of E is trivial and the trace of
![]() $\phi $
vanishes.
$\phi $
vanishes.
Since the pioneering work of Hitchin [Reference Hitchin37], the (nonalgebraic) homeomorphism between
![]() ${M}_{\mathrm {B}}(C,G)$
and
${M}_{\mathrm {B}}(C,G)$
and
![]() ${M}_{\mathrm {Dol}}(C,G)$
has been exploited to study the topology of character varieties. The main result of this article is the computation of some geometric invariants of
${M}_{\mathrm {Dol}}(C,G)$
has been exploited to study the topology of character varieties. The main result of this article is the computation of some geometric invariants of
![]() ${M}_{\mathrm {Dol}}(C,G)$
and
${M}_{\mathrm {Dol}}(C,G)$
and
![]() ${M}_{\mathrm {B}}(C,G)$
, namely, the intersection E-polynomials and the intersection Poincaré polynomials of
${M}_{\mathrm {B}}(C,G)$
, namely, the intersection E-polynomials and the intersection Poincaré polynomials of
![]() ${M}_{\mathrm {Dol}}(C,G)$
and
${M}_{\mathrm {Dol}}(C,G)$
and
![]() ${M}_{\mathrm {B}}(C,G)$
for
${M}_{\mathrm {B}}(C,G)$
for
![]() $G=\operatorname {GL}_2, \operatorname {SL}_2, \operatorname {PGL}_2$
; see §1.2.
$G=\operatorname {GL}_2, \operatorname {SL}_2, \operatorname {PGL}_2$
; see §1.2.
The motivation for this work stems from the newly stated P=W conjectures [Reference Felisetti and Mauri26, Conjecture 1.2, 1.4, 1.5] for singular character varieties; see also [Reference de Cataldo and Maulik15, Question 4.1.7] and the seminal paper [Reference de Cataldo, Hausel and Migliorini13]. In fact, the explicit knowledge of intersection E-polynomials and intersection Poincaré polynomials is an essential ingredient in the proof of the P=W conjectures in rank 2 and genus 2 in [Reference Felisetti and Mauri26, Main Theorem]. Here, as an applications of our computations, we collect in Theorem 1.1 several results related to the P=W conjectures in rank 2 and arbitrary genus. For brevity, we simply write
![]() $M_{\mathrm {B}}$
for
$M_{\mathrm {B}}$
for
![]() ${M}_{\mathrm {B}}(C,G)$
and
${M}_{\mathrm {B}}(C,G)$
and
![]() ${M}_{\mathrm {Dol}}$
for
${M}_{\mathrm {Dol}}$
for
![]() ${M}_{\mathrm {Dol}}(C,G)$
when
${M}_{\mathrm {Dol}}(C,G)$
when
![]() $G=\operatorname {GL}_2$
or
$G=\operatorname {GL}_2$
or
![]() $\operatorname {SL}_2$
, and we suppress subscripts
$\operatorname {SL}_2$
, and we suppress subscripts
![]() ${}_{\text {B}}$
or
${}_{\text {B}}$
or
![]() ${}_{\text {Dol}}$
when we refer indifferently to the Betti or the Dolbeault side.
${}_{\text {Dol}}$
when we refer indifferently to the Betti or the Dolbeault side.
Theorem 1.1 Remarks on the P=W conjectures
The following facts hold:
-
A. the intersection E-polynomial
 $IE(M_{\mathrm {B}})$
is palindromic;
$IE(M_{\mathrm {B}})$
is palindromic; -
B. the PI=WI conjecture for
 $\operatorname {SL}_2$
is equivalent to the PI=WI conjecture for
$\operatorname {SL}_2$
is equivalent to the PI=WI conjecture for
 $\operatorname {GL}_2$
;
$\operatorname {GL}_2$
; -
C.
 $IH^{< 4g-6}(M)$
is freely generated by tautological classes;
$IH^{< 4g-6}(M)$
is freely generated by tautological classes; -
D. the mixed Hodge structure on
 $H^*({M}_{\mathrm {Dol}})$
is not pure for
$H^*({M}_{\mathrm {Dol}})$
is not pure for
 $g>3$
;
$g>3$
; -
E. the P=W conjecture for any resolution of
 $M(C, \operatorname {GL}_n)$
fails when
$M(C, \operatorname {GL}_n)$
fails when
 $M(C, \operatorname {GL}_n)$
does not admit a symplectic resolution.Footnote
1
$M(C, \operatorname {GL}_n)$
does not admit a symplectic resolution.Footnote
1
In Section 5 we recall the content of the P=W conjectures and we give a proof of Theorem 1.1. Here we briefly explain the relevance of the previous statements in view of the P=W conjectures.
-
A. Theorem 1.1.A (Theorem 5.4) provides numerical evidence for the PI=WI conjecture. Indeed, the PI=WI conjecture implies the palindromicity of
 $IE(M_B)$
.
$IE(M_B)$
. -
B. Theorem 1.1.B (Corollary 5.6) is a useful reduction statement. It says that it is enough to prove the PI=WI conjecture only for a portion of the intersection cohomology, namely, its
 $\Gamma $
-invariant part; see (5) and (6).
$\Gamma $
-invariant part; see (5) and (6). -
C. The known proofs of the P=W conjecture for twisted character varieties [Reference de Cataldo, Hausel and Migliorini13] and [Reference de Cataldo, Maulik and Shen16] (cf. also Subsection 5.1) rely on the generation by tautological classes of the
 $\Gamma $
-invariant part of
$\Gamma $
-invariant part of
 $H^*(M)$
. This is unknown for the intersection cohomology of the singular moduli spaces. Theorem 1.1.C (Theorem 5.7) provides a partial answer; that is, the tautological generation of the intersection cohomology in low degree.
$H^*(M)$
. This is unknown for the intersection cohomology of the singular moduli spaces. Theorem 1.1.C (Theorem 5.7) provides a partial answer; that is, the tautological generation of the intersection cohomology in low degree. -
D&E. Theorem 1.1.D and 1.1.E stress the difference between the P=W conjectures for character varieties with or without a symplectic resolution; see Subsection 5.5, Subsection 5.6, and also [Reference Felisetti and Mauri26].
Our strategy to compute the intersection E-polynomials of M is to use the Kirwan–O’Grady desingularisation
![]() $\pi _T\colon T \to M$
(Subsection 3.2) and determine all of the summands of the decomposition theorem for
$\pi _T\colon T \to M$
(Subsection 3.2) and determine all of the summands of the decomposition theorem for
![]() $\pi _T$
; cf. [Reference Kirwan44, Remark 2.28]. This is a subtle task that we can complete thanks to a tight control of the geometry of
$\pi _T$
; cf. [Reference Kirwan44, Remark 2.28]. This is a subtle task that we can complete thanks to a tight control of the geometry of
![]() $\pi _T$
.
$\pi _T$
.
Theorem 1.2 Decomposition theorem for
 $\pi _T$
$\pi _T$
There is an isomorphism in
![]() $D^bMHM_{\mathrm {alg}}(M)$
or in
$D^bMHM_{\mathrm {alg}}(M)$
or in
![]() $D^b(M)$
(ignoring the Tate shifts)
$D^b(M)$
(ignoring the Tate shifts)
 $$ \begin{align*} R\pi_{T, *}\mathbb{Q}[\dim T]= IC_{M} & \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathbb{Q}_{\Sigma}^{\lceil \frac{2g-3-|i|}{2} \rceil}[\dim \Sigma -2i](-2g+3-i) \\[6pt] & \oplus \bigoplus^{2g-4}_{i=-2g+4} i_{\Sigma^\circ,*}\mathscr{L}^{\lfloor \frac{2g-3-|i|}{2} \rfloor}[\dim \Sigma-2i](-2g+3-i)\\[6pt] & \oplus \bigoplus^{3g-4}_{j=-3g+4} \mathbb{Q}^{b(j)}_{\Omega}[\dim \Omega-2j](-3g+3-j), \end{align*} $$
$$ \begin{align*} R\pi_{T, *}\mathbb{Q}[\dim T]= IC_{M} & \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathbb{Q}_{\Sigma}^{\lceil \frac{2g-3-|i|}{2} \rceil}[\dim \Sigma -2i](-2g+3-i) \\[6pt] & \oplus \bigoplus^{2g-4}_{i=-2g+4} i_{\Sigma^\circ,*}\mathscr{L}^{\lfloor \frac{2g-3-|i|}{2} \rfloor}[\dim \Sigma-2i](-2g+3-i)\\[6pt] & \oplus \bigoplus^{3g-4}_{j=-3g+4} \mathbb{Q}^{b(j)}_{\Omega}[\dim \Omega-2j](-3g+3-j), \end{align*} $$
where
-
•
 $\Sigma $
is the singular locus of M;
$\Sigma $
is the singular locus of M; -
•
 $\Omega $
is the singular locus of
$\Omega $
is the singular locus of
 $\Sigma $
;
$\Sigma $
; -
•
 $i_{\Sigma ^\circ }\colon \Sigma ^\circ := \Sigma \setminus \Omega \to \Sigma $
is the natural inclusion;
$i_{\Sigma ^\circ }\colon \Sigma ^\circ := \Sigma \setminus \Omega \to \Sigma $
is the natural inclusion; -
•
 $\mathscr {L}$
is the rank-1 local system on
$\mathscr {L}$
is the rank-1 local system on
 $\Sigma ^{\circ }$
corresponding to a quasi-étale double cover
$\Sigma ^{\circ }$
corresponding to a quasi-étale double cover
 $q\colon \Sigma _{\iota } \to \Sigma $
branched along
$q\colon \Sigma _{\iota } \to \Sigma $
branched along
 $\Omega $
(see Definition 3.3);
$\Omega $
(see Definition 3.3); -
•
 $ b(-3g+3+j)$
is the coefficient of the monomial
$ b(-3g+3+j)$
is the coefficient of the monomial
 $q^j$
in the polynomial
$q^j$
in the polynomial  $$ \begin{align*} &\frac{\left(1-q^{2g-2}\right) \left(1-q^{2g}\right) \left(1-q^4 -q^{2 g-3}-q^{2g-1}+2q^{2g}\right)}{\left(1-q\right)^3 \left(1-q^2\right)}-\frac{1-q^{2g}}{1-q^2}\\[6pt] &\quad -\frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)}. \end{align*} $$
$$ \begin{align*} &\frac{\left(1-q^{2g-2}\right) \left(1-q^{2g}\right) \left(1-q^4 -q^{2 g-3}-q^{2g-1}+2q^{2g}\right)}{\left(1-q\right)^3 \left(1-q^2\right)}-\frac{1-q^{2g}}{1-q^2}\\[6pt] &\quad -\frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)}. \end{align*} $$
Note in addition that the same decomposition holds for the Mukai moduli space of semistable sheaves on K3 or abelian surfaces with Mukai vector
![]() $v = 2 w \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
, where w is primitive and
$v = 2 w \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
, where w is primitive and
![]() $w^2=2(g-1)$
, thus suggesting other potential applications of Theorem 1.2. This is indeed a consequence of the stable isosingularity principle (Theorem 2.11), which roughly says that Betti, Dolbeault and Mukai moduli spaces have the same type of singularities, in the sense of Definition 2.6.
$w^2=2(g-1)$
, thus suggesting other potential applications of Theorem 1.2. This is indeed a consequence of the stable isosingularity principle (Theorem 2.11), which roughly says that Betti, Dolbeault and Mukai moduli spaces have the same type of singularities, in the sense of Definition 2.6.
It is conceivable that the computation of the intersection E-polynomials in rank 3 can be pursued with no substantial conceptual difference. In higher rank, however, this seems hard. In fact, closed formulas may be cumbersome and less enlightening. Notwithstanding, we believe that the rank 2 case can inspire the investigation of the higher rank case, especially in relation to the P=W conjectures [Reference Felisetti and Mauri26] and the Hausel–Thaddeus topological mirror symmetry conjecture for singular character varieties [Reference Hausel32, Remark 3.30].
1.1 Notation
The intersection cohomology of a complex variety X with middle perversity and rational coefficients is denoted by
![]() $IH^*(X)$
. Ordinary singular cohomology with rational coefficients is denoted by
$IH^*(X)$
. Ordinary singular cohomology with rational coefficients is denoted by
![]() $H^*(X)$
. The subscript c stands for compactly supported intersection or ordinary cohomology, respectively
$H^*(X)$
. The subscript c stands for compactly supported intersection or ordinary cohomology, respectively
![]() $IH_c^*(X)$
and
$IH_c^*(X)$
and
![]() $H_c^*(X)$
. Recall that they all carry mixed Hodge structures.
$H_c^*(X)$
. Recall that they all carry mixed Hodge structures.
The Poincaré polynomial, the intersection Poincaré polynomial, the intersection Euler characteristic, the E-polynomial and the intersection E-polynomial are defined by
 $$ \begin{align*} P_t(X) & = \sum_{d} \dim H^d(X) t^d, \\[6pt] IP_t(X) & = \sum_{d} \dim IH^d(X) t^d, \\[6pt] I\chi(X) & = \sum_{d} (-1)^d \dim IH^d(X), \\[-12pt] \\ E(X) & = \sum_{r,s,d}(-1)^d \dim ( \operatorname{Gr}^W_{r+s} H^d_{c}(X, \mathbb{C}))^{r,s} u^r v^s,\\ IE(X) & = \sum_{r,s,d}(-1)^d \dim ( \operatorname{Gr}^W_{r+s} IH^d_{c}(X, \mathbb{C}))^{r,s} u^rv^s. \end{align*} $$
$$ \begin{align*} P_t(X) & = \sum_{d} \dim H^d(X) t^d, \\[6pt] IP_t(X) & = \sum_{d} \dim IH^d(X) t^d, \\[6pt] I\chi(X) & = \sum_{d} (-1)^d \dim IH^d(X), \\[-12pt] \\ E(X) & = \sum_{r,s,d}(-1)^d \dim ( \operatorname{Gr}^W_{r+s} H^d_{c}(X, \mathbb{C}))^{r,s} u^r v^s,\\ IE(X) & = \sum_{r,s,d}(-1)^d \dim ( \operatorname{Gr}^W_{r+s} IH^d_{c}(X, \mathbb{C}))^{r,s} u^rv^s. \end{align*} $$
We will often write
![]() $q := uv$
.
$q := uv$
.
The action of a finite group
![]() $\Gamma $
on X induces the splitting
$\Gamma $
on X induces the splitting
where
![]() $H^d(X)^{\Gamma }$
is fixed by the action of
$H^d(X)^{\Gamma }$
is fixed by the action of
![]() $\Gamma $
and
$\Gamma $
and
![]() $H_{\mathrm {var}}^d(X)$
is the variant part; that is, the unique
$H_{\mathrm {var}}^d(X)$
is the variant part; that is, the unique
![]() $\Gamma $
-invariant complement of
$\Gamma $
-invariant complement of
![]() $H^d(X)^{\Gamma }$
in
$H^d(X)^{\Gamma }$
in
![]() $H^d(X)$
. Analogous splittings hold for the
$H^d(X)$
. Analogous splittings hold for the
![]() $\Gamma $
-modules
$\Gamma $
-modules
![]() $H^d_c(X)$
,
$H^d_c(X)$
,
![]() $IH^d(X)$
and
$IH^d(X)$
and
![]() $IH^d_c(X)$
. The label
$IH^d_c(X)$
. The label
![]() ${}^{\Gamma }$
or
${}^{\Gamma }$
or
![]() ${}_{\mathrm {var}}$
, written after the polynomials above, imposes to replace ordinary (or intersection) cohomology with its
${}_{\mathrm {var}}$
, written after the polynomials above, imposes to replace ordinary (or intersection) cohomology with its
![]() $\Gamma $
-invariant or
$\Gamma $
-invariant or
![]() $\Gamma $
-variant part respectively; for example,
$\Gamma $
-variant part respectively; for example,
 $IE(X)^{\Gamma } = \sum _{r,s,d}(-1)^d \dim ( \operatorname {Gr}^W_{r+s} IH^d_{c}(X, \mathbb {C})^{\Gamma })^{r,s} u^rv^s$
.
$IE(X)^{\Gamma } = \sum _{r,s,d}(-1)^d \dim ( \operatorname {Gr}^W_{r+s} IH^d_{c}(X, \mathbb {C})^{\Gamma })^{r,s} u^rv^s$
.
If
![]() $\iota \colon X \to X$
is an involution, we simply use the superscript
$\iota \colon X \to X$
is an involution, we simply use the superscript
![]() $+$
or
$+$
or
![]() $-$
to denote the
$-$
to denote the
![]() $\iota $
-invariant and
$\iota $
-invariant and
![]() $\iota $
-variant part; for example,
$\iota $
-variant part; for example,
 $P(X)^{+} = \sum _d \dim H^d(X)^{+} t^d := P(X)^{\langle \iota \rangle }$
.
$P(X)^{+} = \sum _d \dim H^d(X)^{+} t^d := P(X)^{\langle \iota \rangle }$
.
We always denote by C a complex projective curve of genus
![]() $g \geq 2$
, unless differently stated. For notational convenience, we simply write
$g \geq 2$
, unless differently stated. For notational convenience, we simply write
![]() $M_{\mathrm {B}}$
for
$M_{\mathrm {B}}$
for
![]() ${M}_{\mathrm {B}}(C,G)$
and
${M}_{\mathrm {B}}(C,G)$
and
![]() ${M}_{\mathrm {Dol}}$
for
${M}_{\mathrm {Dol}}$
for
![]() ${M}_{\mathrm {Dol}}(C,G)$
when
${M}_{\mathrm {Dol}}(C,G)$
when
![]() $G=\operatorname {GL}_2$
or
$G=\operatorname {GL}_2$
or
![]() $\operatorname {SL}_2$
, and we suppress subscripts
$\operatorname {SL}_2$
, and we suppress subscripts
![]() ${}_{\text {B}}$
or
${}_{\text {B}}$
or
![]() ${}_{\text {Dol}}$
when we refer indifferently to the Betti or the Dolbeault side. We adopt the same convention for the strata
${}_{\text {Dol}}$
when we refer indifferently to the Betti or the Dolbeault side. We adopt the same convention for the strata
![]() $\Sigma _{\mathrm {B}}(C,G)$
,
$\Sigma _{\mathrm {B}}(C,G)$
,
![]() $\Sigma _{\mathrm {Dol}}(C,G)$
,
$\Sigma _{\mathrm {Dol}}(C,G)$
,
![]() $\Omega _{\mathrm {B}}(C,G)$
,
$\Omega _{\mathrm {B}}(C,G)$
,
![]() $\Omega _{\mathrm {Dol}}(C,G)$
.
$\Omega _{\mathrm {Dol}}(C,G)$
.
1.2 Computations
As an application of the decomposition theorem (Theorem 1.2), we can express
![]() $IE(M)$
as a function of the E-polynomials of M,
$IE(M)$
as a function of the E-polynomials of M,
![]() $\Sigma _{\iota }$
and
$\Sigma _{\iota }$
and
![]() $\Omega $
; see Proposition 3.2 for the definition of these strata and Subsection 4.1 for the proofs of the following expressions.
$\Omega $
; see Proposition 3.2 for the definition of these strata and Subsection 4.1 for the proofs of the following expressions.
Theorem 1.3.
 $$ \begin{align} IE(M) = E(M)+ (q^2E(\Sigma_{\iota})^+ + qE(\Sigma_{\iota})^-) \cdot \frac{1 - q^{2 g - 4}}{ 1-q^2} +E(\Omega) \cdot q^{2g-2}. \end{align} $$
$$ \begin{align} IE(M) = E(M)+ (q^2E(\Sigma_{\iota})^+ + qE(\Sigma_{\iota})^-) \cdot \frac{1 - q^{2 g - 4}}{ 1-q^2} +E(\Omega) \cdot q^{2g-2}. \end{align} $$
Theorem 1.4. The intersection E-polynomials of
![]() $M_{\mathrm {B}}$
are
$M_{\mathrm {B}}$
are
 $$ \begin{align*} IE(M_{\mathrm{B}}(C, \operatorname{SL}_2)) = & (q^{2g-2}+1)(q^2-1)^{2g-2}+\frac{1}{2}q^{2g-3}(q^2+1)((q+1)^{2g-2}\\ & -(q-1)^{2g-2}) +2^{2g-1}q^{2g-2}((q+1)^{2g-2}+(q-1)^{2g-2}),\\ IE(M_{\mathrm{B}}(C, \operatorname{PGL}_2)) = & (q^{2g-2}+1)(q^2-1)^{2g-2} + \frac{1}{2}q^{2 g - 3}(q^2+q+1)(q + 1)^{2 g - 2} \\ & - \frac{1}{2}q^{2 g - 3}(q^2-q+1)(q - 1)^{2 g - 2},\\ IE(M_{\mathrm{B}}(C, \operatorname{GL}_2)) = & (q-1)^{2g} \cdot IE(M_{\mathrm{B}}(C, \operatorname{PGL}_2)). \end{align*} $$
$$ \begin{align*} IE(M_{\mathrm{B}}(C, \operatorname{SL}_2)) = & (q^{2g-2}+1)(q^2-1)^{2g-2}+\frac{1}{2}q^{2g-3}(q^2+1)((q+1)^{2g-2}\\ & -(q-1)^{2g-2}) +2^{2g-1}q^{2g-2}((q+1)^{2g-2}+(q-1)^{2g-2}),\\ IE(M_{\mathrm{B}}(C, \operatorname{PGL}_2)) = & (q^{2g-2}+1)(q^2-1)^{2g-2} + \frac{1}{2}q^{2 g - 3}(q^2+q+1)(q + 1)^{2 g - 2} \\ & - \frac{1}{2}q^{2 g - 3}(q^2-q+1)(q - 1)^{2 g - 2},\\ IE(M_{\mathrm{B}}(C, \operatorname{GL}_2)) = & (q-1)^{2g} \cdot IE(M_{\mathrm{B}}(C, \operatorname{PGL}_2)). \end{align*} $$
Corollary 1.5. The intersection E-polynomials
![]() $IE(M_{\mathrm {B}})$
are palindromic.
$IE(M_{\mathrm {B}})$
are palindromic.
Corollary 1.6. The intersection Euler characteristics of M are
 $$ \begin{align*} I\chi(M(C, \operatorname{SL}_2)) & =2^{2g-2}(2^{2g-1}+1),\\ I\chi(M(C, \operatorname{PGL}_2)) & =3 \cdot 2^{2g-3}. \end{align*} $$
$$ \begin{align*} I\chi(M(C, \operatorname{SL}_2)) & =2^{2g-2}(2^{2g-1}+1),\\ I\chi(M(C, \operatorname{PGL}_2)) & =3 \cdot 2^{2g-3}. \end{align*} $$
We list the intersection E-polynomial of
![]() $M_{\mathrm {B}}(C, \operatorname {SL}_2)$
in low genus (we truncate the polynomial at degree
$M_{\mathrm {B}}(C, \operatorname {SL}_2)$
in low genus (we truncate the polynomial at degree
![]() $3g-3$
: the coefficients of the monomials of higher degree can be determined by symmetry, since
$3g-3$
: the coefficients of the monomials of higher degree can be determined by symmetry, since
![]() $IE(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
is palindromic of degree
$IE(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
is palindromic of degree
![]() $6g-6$
):
$6g-6$
):
 $$ \begin{align*} g=2: & \quad 1+17q^2+\cdots\\ g=3: & \quad 1-4q^2+75q^4+384q^6+\cdots\\ g=4: & \quad 1-6q^2+15q^4+243q^6+3875q^8+\cdots\\ g=5: & \quad 1-8q^2+28q^4-56q^6+1103q^8+28672q^{10}+71848q^{12}+\cdots. \end{align*} $$
$$ \begin{align*} g=2: & \quad 1+17q^2+\cdots\\ g=3: & \quad 1-4q^2+75q^4+384q^6+\cdots\\ g=4: & \quad 1-6q^2+15q^4+243q^6+3875q^8+\cdots\\ g=5: & \quad 1-8q^2+28q^4-56q^6+1103q^8+28672q^{10}+71848q^{12}+\cdots. \end{align*} $$
Remark 1.7. The intersection E-polynomial of
![]() $M_{\mathrm {B}}(C, \operatorname {SL}_2)$
is a polynomial in
$M_{\mathrm {B}}(C, \operatorname {SL}_2)$
is a polynomial in
![]() $q^2$
. This fails for twisted
$q^2$
. This fails for twisted
![]() $\operatorname {SL}_2$
-character varieties (cf. [Reference Mereb52, (2)]; see also Subsection 5.1 for the definition of the twist), but it holds true for twisted
$\operatorname {SL}_2$
-character varieties (cf. [Reference Mereb52, (2)]; see also Subsection 5.1 for the definition of the twist), but it holds true for twisted
![]() $\operatorname {PGL}_2$
-character varieties, since their cohomology is generated by classes of weight
$\operatorname {PGL}_2$
-character varieties, since their cohomology is generated by classes of weight
![]() $4$
; see [Reference Hausel and Rodriguez-Villegas34, Proposition 4.1.8]. The E-polynomial of
$4$
; see [Reference Hausel and Rodriguez-Villegas34, Proposition 4.1.8]. The E-polynomial of
![]() $M_{\mathrm {B}}(C, \operatorname {SL}_2)$
is a polynomial in
$M_{\mathrm {B}}(C, \operatorname {SL}_2)$
is a polynomial in
![]() $q^2$
, too; see [Reference Martínez and Muñoz48, Theorem 2] or [Reference Baraglia and Hekmati4, Theorem 1.3].
$q^2$
, too; see [Reference Martínez and Muñoz48, Theorem 2] or [Reference Baraglia and Hekmati4, Theorem 1.3].
Theorem 1.8. The intersection E-polynomial of
![]() ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
is
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
is
 $$ \begin{align*} IE( {M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) & = E( {M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)^{\mathrm{sm}}) + \frac{1}{2}(uv)^g \left((1-u)^g(1-v)^g+(1+u)^g(1+v)^g\right)\\ &\quad + \frac{1}{2}(uv)^{g+1}(1-(uv)^{2g-4})\left(\frac{(1-u)^g(1-v)^g}{1-uv}-\frac{(1+u)^g(1+v)^g}{1+uv}\right)\\ &\quad +2^{2g}(uv)^{2g-2}. \end{align*} $$
$$ \begin{align*} IE( {M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) & = E( {M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)^{\mathrm{sm}}) + \frac{1}{2}(uv)^g \left((1-u)^g(1-v)^g+(1+u)^g(1+v)^g\right)\\ &\quad + \frac{1}{2}(uv)^{g+1}(1-(uv)^{2g-4})\left(\frac{(1-u)^g(1-v)^g}{1-uv}-\frac{(1+u)^g(1+v)^g}{1+uv}\right)\\ &\quad +2^{2g}(uv)^{2g-2}. \end{align*} $$
An explicit formula for the E-polynomial of the smooth locus of
![]() ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
was computed in [Reference Kiem and Yoo41, Theorem 3.7]. Together with Theorem 1.8 and Proposition 2.4, this gives the intersection Poincaré polynomial of
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
was computed in [Reference Kiem and Yoo41, Theorem 3.7]. Together with Theorem 1.8 and Proposition 2.4, this gives the intersection Poincaré polynomial of
![]() $M(C, \operatorname {SL}_2)$
.
$M(C, \operatorname {SL}_2)$
.
Theorem 1.9. The intersection Poincaré polynomial of
![]() $M(C, \operatorname {SL}_2)$
is
$M(C, \operatorname {SL}_2)$
is
 $$ \begin{align*} IP_t(M(C, \operatorname{SL}_2)) & = \frac{(t^3+1)^{2g}}{(t^2-1)(t^4-1)} + (g-1)t^{4g-3}\frac{(t+1)^{2g-2}}{t-1}\\ &\quad - \frac{t^{4g-4}}{4(t^2-1)(t^4-1)}\big( (t^2+1)^2(t+1)^{2g}-(t+1)^4(t-1)^{2g} \big)\\ &\quad + \frac{1}{2} t^{4g-4}((t+1)^{2g-2}-(t-1)^{2g-2})- \frac{1}{2} t^{4g-6}((t+1)^{2g}-(t-1)^{2g})\\ &\quad + \frac{1}{2}(2^{2g} -1) t^{4g-4}((t+1)^{2g-2}+(t-1)^{2g-2}). \end{align*} $$
$$ \begin{align*} IP_t(M(C, \operatorname{SL}_2)) & = \frac{(t^3+1)^{2g}}{(t^2-1)(t^4-1)} + (g-1)t^{4g-3}\frac{(t+1)^{2g-2}}{t-1}\\ &\quad - \frac{t^{4g-4}}{4(t^2-1)(t^4-1)}\big( (t^2+1)^2(t+1)^{2g}-(t+1)^4(t-1)^{2g} \big)\\ &\quad + \frac{1}{2} t^{4g-4}((t+1)^{2g-2}-(t-1)^{2g-2})- \frac{1}{2} t^{4g-6}((t+1)^{2g}-(t-1)^{2g})\\ &\quad + \frac{1}{2}(2^{2g} -1) t^{4g-4}((t+1)^{2g-2}+(t-1)^{2g-2}). \end{align*} $$
Therefore, we have
 $$ \begin{align} IP_t(M(C, \operatorname{SL}_2)) = \frac{(t^3+1)^{2g}}{(t^2-1)(t^4-1)}-2g \cdot t^{4g-5}+O(t^{4g-4}). \end{align} $$
$$ \begin{align} IP_t(M(C, \operatorname{SL}_2)) = \frac{(t^3+1)^{2g}}{(t^2-1)(t^4-1)}-2g \cdot t^{4g-5}+O(t^{4g-4}). \end{align} $$
We list the intersection Poincaré polynomial of
![]() $M_{\mathrm {B}}(C, \operatorname {SL}_2)$
in low genus:
$M_{\mathrm {B}}(C, \operatorname {SL}_2)$
in low genus:
 $$ \begin{align*} g=2: \quad & 1+t^2+17 t^4+17t^6\\ g=3: \quad & 1+t^2+6 t^3+2 t^4+6 t^5+17 t^6+6 t^7+81 t^8+12 t^9+396 t^{10}+6t^{11}+66 t^{12}\\ g=4: \quad & 1+t^2+8 t^3+2 t^4+8 t^5+30 t^6+16 t^7+31 t^8+72 t^9+59 t^{10}+72 t^{11}+385 t^{12}\\ &+80 t^{13}+3955 t^{14}+80 t^{15}+3885 t^{16}+16 t^{17}+259t^{18}\\ g=5: \quad & 1+t^2+10 t^3+2 t^4+10 t^5+47 t^6+20 t^7+48 t^8+140 t^9+93 t^{10}+150t^{11}\\ & +304 t^{12} +270 t^{13}+349 t^{14}+522 t^{15}+1583 t^{16}+532t^{17}+29414 t^{18}+532 t^{19}\\ & +72170 t^{20}+280 t^{21}+28784t^{22}+30 t^{23}+1028 t^{24}. \end{align*} $$
$$ \begin{align*} g=2: \quad & 1+t^2+17 t^4+17t^6\\ g=3: \quad & 1+t^2+6 t^3+2 t^4+6 t^5+17 t^6+6 t^7+81 t^8+12 t^9+396 t^{10}+6t^{11}+66 t^{12}\\ g=4: \quad & 1+t^2+8 t^3+2 t^4+8 t^5+30 t^6+16 t^7+31 t^8+72 t^9+59 t^{10}+72 t^{11}+385 t^{12}\\ &+80 t^{13}+3955 t^{14}+80 t^{15}+3885 t^{16}+16 t^{17}+259t^{18}\\ g=5: \quad & 1+t^2+10 t^3+2 t^4+10 t^5+47 t^6+20 t^7+48 t^8+140 t^9+93 t^{10}+150t^{11}\\ & +304 t^{12} +270 t^{13}+349 t^{14}+522 t^{15}+1583 t^{16}+532t^{17}+29414 t^{18}+532 t^{19}\\ & +72170 t^{20}+280 t^{21}+28784t^{22}+30 t^{23}+1028 t^{24}. \end{align*} $$
The Poincaré polynomial of
![]() $M_{\mathrm {B}}(C, \operatorname {SL}_2)$
was obtained in [Reference Daskalopoulos, Wentworth and Wilkin12, Theorem 1.5], which, however, contains small transcription errors (cf. [Reference Cappell, Lee and Miller7, Theorem 2.2] and [Reference Daskalopoulos, Weitsman, Wentworth and Wilkin10, (47)]).
$M_{\mathrm {B}}(C, \operatorname {SL}_2)$
was obtained in [Reference Daskalopoulos, Wentworth and Wilkin12, Theorem 1.5], which, however, contains small transcription errors (cf. [Reference Cappell, Lee and Miller7, Theorem 2.2] and [Reference Daskalopoulos, Weitsman, Wentworth and Wilkin10, (47)]).
 $$ \begin{align*} P_t(M(C, \operatorname{SL}_2))& = \frac{(t^3+1)^{2 g}}{(t^2-1) (t^4-1)} + \frac{(t+1)^{2 g} (t^2+1) + (t-1)^{2 g} (t^2-1)}{2 ( t^4-1)}\\ &\quad + \sum^g_{k=2} \left\{ \binom{2g}{k} - \binom{2g}{k-2} \right\} t^{k + 2 \mathrm{Mod}[k, 2]} \frac{(t^{2 k - 2 \mathrm{Mod}[k, 2]}-1) ( t^{2 g - 2 k + 2}-1)}{(t-1) (t^4-1)}\\ &\quad - \frac{1}{2} t ((t+1)^{2 g} + (t-1)^{2 g})+\frac{t^{2 g + 2}-1}{t-1} -t^{4 g - 4} + \frac{(t-1)^{2 g}t^{4 g - 4}}{4 (t^2+1)} \\ &\quad - \frac{(t+1)^{2 g} t^{4 g - 4}}{2 (t^2-1)}\bigg(\frac{2 g}{t+1} + \frac{1}{t^2-1} - \frac{1}{2} + 3 - 2 g \bigg) \\ &\quad + \frac{1}{2}(2^{2 g} - 1) t^{4 g - 4} ((t+1)^{2 g - 2} + (t-1)^{2 g - 2} - 2), \end{align*} $$
$$ \begin{align*} P_t(M(C, \operatorname{SL}_2))& = \frac{(t^3+1)^{2 g}}{(t^2-1) (t^4-1)} + \frac{(t+1)^{2 g} (t^2+1) + (t-1)^{2 g} (t^2-1)}{2 ( t^4-1)}\\ &\quad + \sum^g_{k=2} \left\{ \binom{2g}{k} - \binom{2g}{k-2} \right\} t^{k + 2 \mathrm{Mod}[k, 2]} \frac{(t^{2 k - 2 \mathrm{Mod}[k, 2]}-1) ( t^{2 g - 2 k + 2}-1)}{(t-1) (t^4-1)}\\ &\quad - \frac{1}{2} t ((t+1)^{2 g} + (t-1)^{2 g})+\frac{t^{2 g + 2}-1}{t-1} -t^{4 g - 4} + \frac{(t-1)^{2 g}t^{4 g - 4}}{4 (t^2+1)} \\ &\quad - \frac{(t+1)^{2 g} t^{4 g - 4}}{2 (t^2-1)}\bigg(\frac{2 g}{t+1} + \frac{1}{t^2-1} - \frac{1}{2} + 3 - 2 g \bigg) \\ &\quad + \frac{1}{2}(2^{2 g} - 1) t^{4 g - 4} ((t+1)^{2 g - 2} + (t-1)^{2 g - 2} - 2), \end{align*} $$
where
![]() $\mathrm {Mod}[k, l]$
is the remainder on division of k by l. We can then inspect the difference
$\mathrm {Mod}[k, l]$
is the remainder on division of k by l. We can then inspect the difference
![]() $IP_t(M(C, \operatorname {SL}_2))-P_t(M(C, \operatorname {SL}_2))$
in low genus:
$IP_t(M(C, \operatorname {SL}_2))-P_t(M(C, \operatorname {SL}_2))$
in low genus:
 $$ \begin{align*} g=2: \quad & 16 t^4\\ g=3: \quad & 6 t^3+t^4+6 t^5+t^6+6 t^7+79 t^8+t^{10}\\ g=4: \quad & 8 t^3+t^4+8 t^5-20 t^6+16 t^7-19 t^8+22 t^9+56 t^{10}+56 t^{11}+327 t^{12}\\ & +8 t^{13}+28 t^{14}+t^{16}\\ g=5: \quad & 10 t^3 + t^4 + 10 t^5 - 65 t^6 + 20 t^7 - 196 t^8 - 35 t^9 - 20 t^{10} - 25 t^{11} + 124 t^{12} \\ & + 240 t^{13} + 256 t^{14} + 262 t^{15} + 1279 t^{16} + 120 t^{17} + 211 t^{18} + 10 t^{19} + 45 t^{20} + t^{22}. \end{align*} $$
$$ \begin{align*} g=2: \quad & 16 t^4\\ g=3: \quad & 6 t^3+t^4+6 t^5+t^6+6 t^7+79 t^8+t^{10}\\ g=4: \quad & 8 t^3+t^4+8 t^5-20 t^6+16 t^7-19 t^8+22 t^9+56 t^{10}+56 t^{11}+327 t^{12}\\ & +8 t^{13}+28 t^{14}+t^{16}\\ g=5: \quad & 10 t^3 + t^4 + 10 t^5 - 65 t^6 + 20 t^7 - 196 t^8 - 35 t^9 - 20 t^{10} - 25 t^{11} + 124 t^{12} \\ & + 240 t^{13} + 256 t^{14} + 262 t^{15} + 1279 t^{16} + 120 t^{17} + 211 t^{18} + 10 t^{19} + 45 t^{20} + t^{22}. \end{align*} $$
Corollary 1.10. Let C be a curve of genus
![]() $g \geq 6$
. Then we have
$g \geq 6$
. Then we have
 $$ \begin{align*}IP_t(M)-P_t(M) = 2g \cdot t^3 +t^4 +2g \cdot t^5 - \left\lbrace \binom{2g}{3}-\binom{2g}{2}-2g\right\rbrace t^6 + O(t^7). \end{align*} $$
$$ \begin{align*}IP_t(M)-P_t(M) = 2g \cdot t^3 +t^4 +2g \cdot t^5 - \left\lbrace \binom{2g}{3}-\binom{2g}{2}-2g\right\rbrace t^6 + O(t^7). \end{align*} $$
At this point it is worth recalling how the (intersection) cohomology of
![]() $M(C, G)$
with
$M(C, G)$
with
![]() $G=\operatorname {GL}_n, \operatorname {SL}_n$
and
$G=\operatorname {GL}_n, \operatorname {SL}_n$
and
![]() $\operatorname {PGL}_n$
compares and how to extend the previous results for the
$\operatorname {PGL}_n$
compares and how to extend the previous results for the
![]() $\operatorname {SL}_2$
case to
$\operatorname {SL}_2$
case to
![]() $\operatorname {PGL}_2$
and
$\operatorname {PGL}_2$
and
![]() $\operatorname {GL}_2$
.
$\operatorname {GL}_2$
.
The morphism
sends a representation or a Higgs bundle to its associated determinant representation or Higgs bundle. It is an étale locally trivial fibration with monodromy group
![]() $\Gamma \simeq (\mathbb {Z}/2\mathbb {Z})^{2g}$
and fibre isomorphic to
$\Gamma \simeq (\mathbb {Z}/2\mathbb {Z})^{2g}$
and fibre isomorphic to
![]() $M(C, \operatorname {SL}_n)$
. The quotient of
$M(C, \operatorname {SL}_n)$
. The quotient of
![]() $M(C, \operatorname {SL}_n)$
for the residual action of
$M(C, \operatorname {SL}_n)$
for the residual action of
![]() $\Gamma $
is
$\Gamma $
is
![]() $M(C, \operatorname {PGL}_n)$
. Hence, there exist morphisms of mixed Hodge structures
$M(C, \operatorname {PGL}_n)$
. Hence, there exist morphisms of mixed Hodge structures
Analogous splittings hold for
![]() $IH^*$
,
$IH^*$
,
![]() $H_c^*$
,
$H_c^*$
,
![]() $IH^*_c$
. A proof of these facts can be found, for instance, in [Reference Felisetti and Mauri26, §3.2].
$IH^*_c$
. A proof of these facts can be found, for instance, in [Reference Felisetti and Mauri26, §3.2].
The analogues of Theorems 1.8 and 1.9 for
![]() $\operatorname {PGL}_2$
can be obtained by substituting all of the occurrences of the coefficient
$\operatorname {PGL}_2$
can be obtained by substituting all of the occurrences of the coefficient
![]() $2^{2g}$
with
$2^{2g}$
with
![]() $1$
in the formulas of the theorems; see Remark 4.3. According to (5), the corresponding polynomials for
$1$
in the formulas of the theorems; see Remark 4.3. According to (5), the corresponding polynomials for
![]() $\operatorname {GL}_2$
are the product of the E-polynomials or the (intersection) Poincaré polynomial for
$\operatorname {GL}_2$
are the product of the E-polynomials or the (intersection) Poincaré polynomial for
![]() $\operatorname {PGL}_2$
with
$\operatorname {PGL}_2$
with
![]() $E(T^*\operatorname {Jac}(C))=(uv)^g(1-u)^g(1-v)^g$
or
$E(T^*\operatorname {Jac}(C))=(uv)^g(1-u)^g(1-v)^g$
or
![]() $P_t(\operatorname {Jac}(C))=(t+1)^{2g}$
, respectively.
$P_t(\operatorname {Jac}(C))=(t+1)^{2g}$
, respectively.
Here, as a corollary of Theorems 1.4, 1.9 and (6), we study the portion of
![]() $IH^*(M(C, \operatorname {SL}_2))$
on which
$IH^*(M(C, \operatorname {SL}_2))$
on which
![]() $\Gamma $
acts nontrivially. The following should be considered the untwisted analogue of [Reference Hausel and Thaddeus35, Proposition 8.2] in rank 2. This suggests that intersection cohomology may be the right cohomology theory to formulate a topological mirror symmetry conjecture for
$\Gamma $
acts nontrivially. The following should be considered the untwisted analogue of [Reference Hausel and Thaddeus35, Proposition 8.2] in rank 2. This suggests that intersection cohomology may be the right cohomology theory to formulate a topological mirror symmetry conjecture for
![]() $M(C, \operatorname {SL}_n)$
and
$M(C, \operatorname {SL}_n)$
and
![]() $M(C, \operatorname {PGL}_n)$
; see [Reference Hausel32, Remark 3.30] and [Reference Mauri49].
$M(C, \operatorname {PGL}_n)$
; see [Reference Hausel32, Remark 3.30] and [Reference Mauri49].
Corollary 1.11. The variant intersection E-polynomial and Poincaré polynomials for the action of
![]() $\Gamma $
are
$\Gamma $
are
 $$ \begin{align*} IE_{\mathrm{var}}(M_{\mathrm{B}}(C, \operatorname{SL}_2)) &= \frac{1}{2} (2^{2g}-1) q^{2g-2} ((q+1)^{2g-2}+(q-1)^{2g-2}),\\ IE_{\mathrm{var}}({M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) &= \frac{1}{2} (2^{2g}-1) (uv)^{3g-3} ((u+1)^{g-1}(v+1)^{g-1} +(u-1)^{g-1}(v-1)^{g-1}),\\ IP_{t, \mathrm{var}}(M(C, \operatorname{SL}_2)) &= \frac{1}{2}(2^{2g}-1) t^{4g-4}((t+1)^{2g-2}+(t-1)^{2g-2}). \end{align*} $$
$$ \begin{align*} IE_{\mathrm{var}}(M_{\mathrm{B}}(C, \operatorname{SL}_2)) &= \frac{1}{2} (2^{2g}-1) q^{2g-2} ((q+1)^{2g-2}+(q-1)^{2g-2}),\\ IE_{\mathrm{var}}({M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) &= \frac{1}{2} (2^{2g}-1) (uv)^{3g-3} ((u+1)^{g-1}(v+1)^{g-1} +(u-1)^{g-1}(v-1)^{g-1}),\\ IP_{t, \mathrm{var}}(M(C, \operatorname{SL}_2)) &= \frac{1}{2}(2^{2g}-1) t^{4g-4}((t+1)^{2g-2}+(t-1)^{2g-2}). \end{align*} $$
In particular,
![]() $q^{-2g+2}IE_{\mathrm {var}}(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
and
$q^{-2g+2}IE_{\mathrm {var}}(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
and
![]() $q^{-6g+6}IE_{\mathrm {var}}({M}_{\mathrm {Dol}}(C, \operatorname {SL}_2);q,q)$
are palindromic polynomials of degree
$q^{-6g+6}IE_{\mathrm {var}}({M}_{\mathrm {Dol}}(C, \operatorname {SL}_2);q,q)$
are palindromic polynomials of degree
![]() $2g-2$
.
$2g-2$
.
As a byproduct, we also obtain the E-polynomials and the Poincaré polynomial of the Kirwan–O’Grady desingularisation
![]() $\pi _T\colon T \to M$
. We write explicitly the E-polynomials of
$\pi _T\colon T \to M$
. We write explicitly the E-polynomials of
![]() $M(C, \operatorname {SL}_2)$
and leave the straightforward computations of the other polynomials to the reader (cf. Subsection 4.2 and Subsection 2.3).
$M(C, \operatorname {SL}_2)$
and leave the straightforward computations of the other polynomials to the reader (cf. Subsection 4.2 and Subsection 2.3).
Theorem 1.12. The E-polynomials of
![]() $T(C, \operatorname {SL}_2)$
are
$T(C, \operatorname {SL}_2)$
are
 $$ \begin{align*} E( T_{\mathrm{B}}(C, \operatorname{SL}_2)) & = (q^{2g-2}+1)(q^2-1)^{2g-2}+\frac{1}{2}q^{2g-3}(q^2+1)((q+1)^{2g-2}\\ &\quad -(q-1)^{2g-2}) +2^{2g-1}q^{2g-2}((q+1)^{2g-2}+(q-1)^{2g-2})\\ &\quad + \frac{1}{2} q((1+q)^{2g-1}(1+q^{2g-3}) +(1-q)^{2g-1}(1-q^{2g-3}))\frac{1-q^{2g-3}}{1-q}\\ & \quad+ 2^{2g}\frac{q}{(1-q)^3(1-q^2)} ( 2 - q - q^3 - q^{2g-4} - 2 q^{2g-2} + q^{2g-1} \\ &\quad - 2 q^{2g} + 4 q^{2g+1} - q^{2g+2} + q^{2g+3} + q^{4g-6} - q^{4g-5} + 4 q^{4g-4} \\ &\quad - 2 q^{4g-3} + q^{4g-2} - 2 q^{4g-1} - q^{4g+1} - q^{6g-6} - q^{6g-4} + 2 q^{6g-3}), \end{align*} $$
$$ \begin{align*} E( T_{\mathrm{B}}(C, \operatorname{SL}_2)) & = (q^{2g-2}+1)(q^2-1)^{2g-2}+\frac{1}{2}q^{2g-3}(q^2+1)((q+1)^{2g-2}\\ &\quad -(q-1)^{2g-2}) +2^{2g-1}q^{2g-2}((q+1)^{2g-2}+(q-1)^{2g-2})\\ &\quad + \frac{1}{2} q((1+q)^{2g-1}(1+q^{2g-3}) +(1-q)^{2g-1}(1-q^{2g-3}))\frac{1-q^{2g-3}}{1-q}\\ & \quad+ 2^{2g}\frac{q}{(1-q)^3(1-q^2)} ( 2 - q - q^3 - q^{2g-4} - 2 q^{2g-2} + q^{2g-1} \\ &\quad - 2 q^{2g} + 4 q^{2g+1} - q^{2g+2} + q^{2g+3} + q^{4g-6} - q^{4g-5} + 4 q^{4g-4} \\ &\quad - 2 q^{4g-3} + q^{4g-2} - 2 q^{4g-1} - q^{4g+1} - q^{6g-6} - q^{6g-4} + 2 q^{6g-3}), \end{align*} $$
 $$ \begin{align*} E( {T}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) & = E( {M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)^{\mathrm{sm}}) \\[5pt] &\quad + \frac{1}{2}(uv)^g \frac{(1-(uv)^{2g-2})}{(1-uv)}\bigg( \frac{(1-u)^g(1-v)^g(1-(uv)^{2g-3})}{1-uv} \\[5pt] &\quad + \frac{(1+u)^g(1+v)^g(1+(uv)^{2g-3})}{1+uv}\bigg)-2^{2g} \frac{(1-(uv)^{2g-2})^2}{(1-(uv)^2)(1-uv)}\\[5pt] &\quad + 2^{2g}\frac{\left(1-(uv)^{2g-2}\right) \left(1-(uv)^{2g}\right)}{\left(1-uv\right)^3 \left(1-(uv)^2\right)}(1-(uv)^4 -(uv)^{2 g-3}\\[5pt] &\quad -(uv)^{2g-1}+2(uv)^{2g}). \end{align*} $$
$$ \begin{align*} E( {T}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) & = E( {M}_{\mathrm{Dol}}(C, \operatorname{SL}_2)^{\mathrm{sm}}) \\[5pt] &\quad + \frac{1}{2}(uv)^g \frac{(1-(uv)^{2g-2})}{(1-uv)}\bigg( \frac{(1-u)^g(1-v)^g(1-(uv)^{2g-3})}{1-uv} \\[5pt] &\quad + \frac{(1+u)^g(1+v)^g(1+(uv)^{2g-3})}{1+uv}\bigg)-2^{2g} \frac{(1-(uv)^{2g-2})^2}{(1-(uv)^2)(1-uv)}\\[5pt] &\quad + 2^{2g}\frac{\left(1-(uv)^{2g-2}\right) \left(1-(uv)^{2g}\right)}{\left(1-uv\right)^3 \left(1-(uv)^2\right)}(1-(uv)^4 -(uv)^{2 g-3}\\[5pt] &\quad -(uv)^{2g-1}+2(uv)^{2g}). \end{align*} $$
In particular, the E-polynomial
![]() $E(T_B)$
is palindromic.
$E(T_B)$
is palindromic.
1.3 Outline and relation with other work
-
• In Section 2 we collect some preliminary results: the intersection cohomology of an affine cone, the decomposition theorem, some properties of the mixed Hodge structures of singular semi-projective varieties (cf. [Reference Hausel and Rodriguez-Villegas34]) and the stable isosingularity principle (implicitly used in [Reference Kiem and Yoo41, p. 834]). Analogous degeneration techniques employed to establish the stable isosingularity principle have been discussed in [Reference de Cataldo, Maulik and Shen16] and [Reference de Cataldo, Maulik and Shen17, §4] in relation to twisted character varieties.
-
• In Section 3 we describe the singularities of M and the geometry of the Kirwan–O’Grady desingularisation
 $\pi _T\colon T \to M$
. This part highly relies on [Reference O’Grady56] and [Reference Kiem and Yoo41]. The computation of the Poincaré polynomial of the incidence variety
$\pi _T\colon T \to M$
. This part highly relies on [Reference O’Grady56] and [Reference Kiem and Yoo41]. The computation of the Poincaré polynomial of the incidence variety
 $I_{2g-3}$
in [Reference Kiem and Yoo41] contains a mistake, and we fix it in Subsection 3.3.
$I_{2g-3}$
in [Reference Kiem and Yoo41] contains a mistake, and we fix it in Subsection 3.3. -
• In Subsection 3.4 we use several times the decomposition theorem to determine the intersection cohomology of the normal slice to strata of a Whitney stratification of M.
The singularities of the Betti and Dolbeault moduli spaces are locally modelled on Nakajima quiver varieties which usually do not admit a symplectic resolution. Although a lot is known about the intersection cohomology of quiver varieties with symplectic resolutions (see, for instance, [Reference Nakajima54]), the local computations in Subsection 3.4 seem new.
-
• In Section 4 we complete the proof of Theorem 1.2. Then in Subsection 4.1 and Subsection 4.2 we argue how to compute the intersection E-polynomials and intersection Poincaré polynomial of M and we prove the results of Subsection 1.2. The E-polynomial of M is known thanks to [Reference Martínez and Muñoz48], [Reference Baraglia and Hekmati4] and [Reference Kiem and Yoo41], while the ordinary Poincaré polynomial of M appears in [Reference Daskalopoulos, Wentworth and Wilkin12]. Despite the active research in the field and the stimuli from the PI=WI conjecture, there are few previous works exhibiting explicit computations of the intersection cohomology of Dolbeault and Betti moduli spaces; see [Reference Felisetti25] and [Reference Felisetti and Mauri26].
In [Reference Kiem40] Kiem studied the intersection cohomology of character varieties with coefficients in a compact Lie group. However, the methods in [Reference Kiem40] do not extend to the complex reductive case, since for a general complex reductive group G the representation space
 $\operatorname {Hom}(\pi _1(C), G)$
is not smooth, and the quotient map
$\operatorname {Hom}(\pi _1(C), G)$
is not smooth, and the quotient map
 is not placid in the sense of [Reference Goresky and MacPherson30].
is not placid in the sense of [Reference Goresky and MacPherson30].We mention another remarkable precedent. The Dolbeault moduli space is a partial compactification of the cotangent bundle of the moduli space of stable vector bundles. The intersection cohomology of the moduli space of semistable vector bundles was determined in [Reference Kirwan43] for rank 2 (or, equivalently, in [Reference Kiem40]) and in [Reference Mozgovoy and Reineke53] in full generality. It is unclear how this result may imply Theorem 1.2.
-
• Section 5 explores many implications concerning the P=W conjectures for M stemming from the previous calculations.
2 Preliminaries
2.1 Intersection cohomology of affine cones
Let X be a complex projective variety of dimension
![]() $n-1$
with an ample line bundle L. The graded ring associated to L is the graded
$n-1$
with an ample line bundle L. The graded ring associated to L is the graded
![]() $\mathbb {C}$
-algebra
$\mathbb {C}$
-algebra
 $$ \begin{align*}R(X, L) := \bigoplus_{m \geq 0} H^0(X, L^m).\end{align*} $$
$$ \begin{align*}R(X, L) := \bigoplus_{m \geq 0} H^0(X, L^m).\end{align*} $$
The affine cone over X with conormal bundle L is
Let
![]() $s_1, \ldots , s_N$
be a set of generators for
$s_1, \ldots , s_N$
be a set of generators for
![]() $R(X,L)$
of degree
$R(X,L)$
of degree
![]() $m_1, \ldots , m_N$
. Then there exists an embedding
$m_1, \ldots , m_N$
. Then there exists an embedding
![]() $C(X,L) \subseteq \mathbb {C}^N$
such that
$C(X,L) \subseteq \mathbb {C}^N$
such that
![]() $C(X,L)$
is invariant with respect to the
$C(X,L)$
is invariant with respect to the
![]() $\mathbb {G}_m$
-action
$\mathbb {G}_m$
-action
Conversely, any affine variety with a
![]() $\mathbb {G}_m$
-action and a fixed point which is attractive for
$\mathbb {G}_m$
-action and a fixed point which is attractive for
![]() $t \to 0$
is isomorphic to an affine cone; see, for instance, [Reference Demazure21, §3.5].
$t \to 0$
is isomorphic to an affine cone; see, for instance, [Reference Demazure21, §3.5].
All of the singularities of this article are locally modelled on affine cones, whose coordinate rings are not necessarily generated in degree 1. For this reason, here we compute their intersection cohomology, thus generalising [Reference de Cataldo and Migliorini19, Example 2.2.1].
Proposition 2.1 Intersection cohomology of an affine cone
 $$ \begin{align*} IH^d(C(X,L)) \simeq \begin{cases} IH^d_{\mathrm{prim}}(X) & \text{ for } d< n\\ 0 & \text{ for } d \geq n, \end{cases} \end{align*} $$
$$ \begin{align*} IH^d(C(X,L)) \simeq \begin{cases} IH^d_{\mathrm{prim}}(X) & \text{ for } d< n\\ 0 & \text{ for } d \geq n, \end{cases} \end{align*} $$
where
 $IH^d_{\mathrm {prim}}(X) := \ker (c_1(L) ^{n-d} \cup \colon IH^d(X) \to IH^{2n-d}(X))$
is the primitive intersection cohomology.
$IH^d_{\mathrm {prim}}(X) := \ker (c_1(L) ^{n-d} \cup \colon IH^d(X) \to IH^{2n-d}(X))$
is the primitive intersection cohomology.
Proof. Denote by
![]() $C(X,L)^* := C(X,L) \setminus \{\text {vertex}\}$
the punctured affine cone. By [Reference Durfee23, Lemma 1] or [Reference Kirwan and Woolf45, Proposition 4.7.2], we can write
$C(X,L)^* := C(X,L) \setminus \{\text {vertex}\}$
the punctured affine cone. By [Reference Durfee23, Lemma 1] or [Reference Kirwan and Woolf45, Proposition 4.7.2], we can write
 $$ \begin{align*} IH^d(C(X,L)) \simeq \begin{cases} IH^d(C(X,L)^*) & \text{ for } d< n\\ 0 & \text{ for } d\geq n. \end{cases} \end{align*} $$
$$ \begin{align*} IH^d(C(X,L)) \simeq \begin{cases} IH^d(C(X,L)^*) & \text{ for } d< n\\ 0 & \text{ for } d\geq n. \end{cases} \end{align*} $$
Suppose now that
![]() $R(X,L)$
is generated in degree 1. Then the blow-up of the origin
$R(X,L)$
is generated in degree 1. Then the blow-up of the origin
 $$ \begin{align*}p\colon BC(X,L) := \operatorname{Spec}_X \bigoplus_{m \geq 0} L^m \to C(X,L)\end{align*} $$
$$ \begin{align*}p\colon BC(X,L) := \operatorname{Spec}_X \bigoplus_{m \geq 0} L^m \to C(X,L)\end{align*} $$
is the total space of the line bundle
![]() $L^*$
. By the hard Lefschetz theorem, the relative long exact sequence of the inclusion
$L^*$
. By the hard Lefschetz theorem, the relative long exact sequence of the inclusion
![]() $C(X, L)^* \hookrightarrow BC(X,L)$
splits into the short exact sequences
$C(X, L)^* \hookrightarrow BC(X,L)$
splits into the short exact sequences
 $$ \begin{align} 0 \to IH^{d-2}(X) \xrightarrow{c_1(L) \cup} IH^{d}(X) \to IH^{d}(C(X, L)^*) \to 0 \quad \text{ for } d < n. \end{align} $$
$$ \begin{align} 0 \to IH^{d-2}(X) \xrightarrow{c_1(L) \cup} IH^{d}(X) \to IH^{d}(C(X, L)^*) \to 0 \quad \text{ for } d < n. \end{align} $$
Therefore, we obtain that for
![]() $d < n$
,
$d < n$
,
 $$ \begin{align*}IH^{d}(C(X, L)) \simeq \mathrm{coker} (c_1(L) \cup\colon IH^{d-2}(X) \to IH^{d}(X)) \simeq IH^d_{\mathrm{prim}}(X).\end{align*} $$
$$ \begin{align*}IH^{d}(C(X, L)) \simeq \mathrm{coker} (c_1(L) \cup\colon IH^{d-2}(X) \to IH^{d}(X)) \simeq IH^d_{\mathrm{prim}}(X).\end{align*} $$
If
![]() $R(X,L)$
is not generated in degree 1, then
$R(X,L)$
is not generated in degree 1, then
![]() $BC(X,L)$
is the total space of a line bundle only up to a finite cover; see [Reference Orlik and Wagreich57, §1.2]. More precisely, consider the finite morphism
$BC(X,L)$
is the total space of a line bundle only up to a finite cover; see [Reference Orlik and Wagreich57, §1.2]. More precisely, consider the finite morphism
![]() $g\colon \mathbb {C}^N \to \mathbb {C}^N$
defined by
$g\colon \mathbb {C}^N \to \mathbb {C}^N$
defined by
Set
![]() $V'= g^{-1}C(X,L)$
, where
$V'= g^{-1}C(X,L)$
, where
![]() $C(X,L)$
is embedded in
$C(X,L)$
is embedded in
![]() $\mathbb {C}^N$
as in (7). We see that
$\mathbb {C}^N$
as in (7). We see that
![]() $C(X,L)$
is the quotient of
$C(X,L)$
is the quotient of
![]() $V'$
by the finite group
$V'$
by the finite group
![]() $A= (\mathbb {Z}/m_1 \mathbb {Z}) \times \ldots \times (\mathbb {Z}/m_N \mathbb {Z})$
acting on
$A= (\mathbb {Z}/m_1 \mathbb {Z}) \times \ldots \times (\mathbb {Z}/m_N \mathbb {Z})$
acting on
![]() $V'$
by coordinatewise multiplication.
$V'$
by coordinatewise multiplication.
![]() $V'$
has a
$V'$
has a
![]() $\mathbb {G}_m$
-action defined by
$\mathbb {G}_m$
-action defined by
![]() $t \cdot (x_1, \ldots , x_N) = (t x_1, \ldots , t x_N)$
and covering the
$t \cdot (x_1, \ldots , x_N) = (t x_1, \ldots , t x_N)$
and covering the
![]() $\mathbb {G}_m$
-action on
$\mathbb {G}_m$
-action on
![]() $C(X,L)$
given by (7). Since the
$C(X,L)$
given by (7). Since the
![]() $\mathbb {G}_m$
-action on
$\mathbb {G}_m$
-action on
![]() $V'$
has weight 1,
$V'$
has weight 1,
![]() $X'$
is the spectrum of a graded algebra generated in degree 1, say,
$X'$
is the spectrum of a graded algebra generated in degree 1, say,
![]() $V' = C(X',L')$
for some projective variety
$V' = C(X',L')$
for some projective variety
![]() $X'$
and ample line bundle
$X'$
and ample line bundle
![]() $L'$
. In particular, there exists a commutative diagram
$L'$
. In particular, there exists a commutative diagram

where p and
![]() $p'$
are blow-ups of the vertices of the cones, i and
$p'$
are blow-ups of the vertices of the cones, i and
![]() $i'$
are the embedding of the exceptional divisors and the vertical arrows are quotients with respect to (the lift of) the action of A. Thus, we have
$i'$
are the embedding of the exceptional divisors and the vertical arrows are quotients with respect to (the lift of) the action of A. Thus, we have
![]() $IH^*(C(X',L'))^A \simeq IH^*(C(X, L))$
.
$IH^*(C(X',L'))^A \simeq IH^*(C(X, L))$
.
The discussion above shows that the sequences (8) are exact for
![]() $C(X',L')$
and it is A-equivariant by the commutativity of (9). Taking invariants, we show then that (8) holds for
$C(X',L')$
and it is A-equivariant by the commutativity of (9). Taking invariants, we show then that (8) holds for
![]() $C(X,L)$
unconditionally.
$C(X,L)$
unconditionally.
2.2 The perverse Leray filtration
In this section we briefly recall the statement of the decomposition theorem and the definition of the perverse filtration.
For a complex algebraic variety X let
![]() $D^b(X, \mathbb {Q})$
be the bounded derived category of complexes of sheaves of
$D^b(X, \mathbb {Q})$
be the bounded derived category of complexes of sheaves of
![]() $\mathbb {Q}$
-vector spaces with algebraically constructible cohomology. Denote the full abelian subcategory of perverse sheaves by
$\mathbb {Q}$
-vector spaces with algebraically constructible cohomology. Denote the full abelian subcategory of perverse sheaves by
![]() $\mathrm {Perv}(X)$
and the perverse cohomology functors by
$\mathrm {Perv}(X)$
and the perverse cohomology functors by
![]() ${}^{\mathfrak {p}}\mathcal {H}^i\colon D^b(S, \mathbb {Q}) \to \mathrm {Perv}(X)$
; see [Reference Beilinson, Bernstein and Deligne5] or [Reference de Cataldo and Migliorini19].
${}^{\mathfrak {p}}\mathcal {H}^i\colon D^b(S, \mathbb {Q}) \to \mathrm {Perv}(X)$
; see [Reference Beilinson, Bernstein and Deligne5] or [Reference de Cataldo and Migliorini19].
Let
![]() $MHM_{\mathrm {alg}}(X)$
be the category of algebraic mixed Hodge modules with rational coefficients and
$MHM_{\mathrm {alg}}(X)$
be the category of algebraic mixed Hodge modules with rational coefficients and
![]() $D^bMHM_{\mathrm {alg}}(X)$
its bounded derived category. Let
$D^bMHM_{\mathrm {alg}}(X)$
its bounded derived category. Let
![]() ${}^{\mathfrak {p}}\mathcal {H}^i\colon D^bMHM_{\mathrm {alg}}(X) \to MHM_{\mathrm {alg}}(X)$
be the cohomology functors; see [Reference Saito62] or [Reference Schnell63].
${}^{\mathfrak {p}}\mathcal {H}^i\colon D^bMHM_{\mathrm {alg}}(X) \to MHM_{\mathrm {alg}}(X)$
be the cohomology functors; see [Reference Saito62] or [Reference Schnell63].
The simple objects of
![]() $D^bMHM_{\mathrm {alg}}(X)$
(respectively
$D^bMHM_{\mathrm {alg}}(X)$
(respectively
![]() $D^b(X, \mathbb {Q})$
) are the intersection cohomology complexes
$D^b(X, \mathbb {Q})$
) are the intersection cohomology complexes
![]() $IC_X(L)$
, where L is a polarisable variation of pure Hodge structures (respectively a local system) on a Zariski-open subset of the smooth locus of X. We denote simply by
$IC_X(L)$
, where L is a polarisable variation of pure Hodge structures (respectively a local system) on a Zariski-open subset of the smooth locus of X. We denote simply by
![]() $IC_X$
the complex
$IC_X$
the complex
![]() $IC_X(\mathbb {Q}_{X \setminus \operatorname {Sing}(X)})$
. In particular,
$IC_X(\mathbb {Q}_{X \setminus \operatorname {Sing}(X)})$
. In particular,
 $IH^d(X) \simeq H^{d}(X, IC_X(\mathbb {Q}_{X \setminus \operatorname {Sing}(X)})[-\dim X])$
.
$IH^d(X) \simeq H^{d}(X, IC_X(\mathbb {Q}_{X \setminus \operatorname {Sing}(X)})[-\dim X])$
.
There is a forgetful functor
![]() $\mathrm {rat}\colon D^bMHM_{\mathrm {alg}}(X) \to D^b(X, \mathbb {Q})$
which commutes with
$\mathrm {rat}\colon D^bMHM_{\mathrm {alg}}(X) \to D^b(X, \mathbb {Q})$
which commutes with
![]() ${}^{\mathfrak {p}}\mathcal {H}^i$
and pushforward
${}^{\mathfrak {p}}\mathcal {H}^i$
and pushforward
![]() $Rf_*$
and maps
$Rf_*$
and maps
![]() $MHM_{\mathrm {alg}}(X)$
in
$MHM_{\mathrm {alg}}(X)$
in
![]() $\mathrm {Perv}(X)$
. We will make no notational distinction between
$\mathrm {Perv}(X)$
. We will make no notational distinction between
![]() $K \in D^bMHM_{\mathrm {alg}}(X)$
and
$K \in D^bMHM_{\mathrm {alg}}(X)$
and
![]() $\mathrm {rat}(K)$
.
$\mathrm {rat}(K)$
.
Now let
![]() $f\colon X \to Y$
be a proper morphism of varieties with defect of semismallness
$f\colon X \to Y$
be a proper morphism of varieties with defect of semismallness
The decomposition theorem of Beilinson–Bernstein–Deligne–Gabber, or its mixed Hodge module version by Saito, says that there is an isomorphism in
![]() $D^bMHM_{\mathrm {alg}}(X)$
(respectively in
$D^bMHM_{\mathrm {alg}}(X)$
(respectively in
![]() $D^b(X, \mathbb {Q})$
)
$D^b(X, \mathbb {Q})$
)
 $$ \begin{align*} Rf_*IC_X = \bigoplus^r_{i=-r} {}^{\mathfrak{p}}\mathcal{H}^i(Rf_*IC_X)[-i] = \bigoplus^r_{i=-r} \bigoplus_l IC_{\overline{Y}_{i,l}}(L_{i,l})[-i], \end{align*} $$
$$ \begin{align*} Rf_*IC_X = \bigoplus^r_{i=-r} {}^{\mathfrak{p}}\mathcal{H}^i(Rf_*IC_X)[-i] = \bigoplus^r_{i=-r} \bigoplus_l IC_{\overline{Y}_{i,l}}(L_{i,l})[-i], \end{align*} $$
where
![]() $L_{i, l}$
are polarisable variations of pure Hodge structures (respectively local systems) on the strata of a stratification
$L_{i, l}$
are polarisable variations of pure Hodge structures (respectively local systems) on the strata of a stratification
![]() $Y = \bigsqcup _{l} Y_{i,l}$
; see [Reference Beilinson, Bernstein and Deligne5] and [Reference Saito61].
$Y = \bigsqcup _{l} Y_{i,l}$
; see [Reference Beilinson, Bernstein and Deligne5] and [Reference Saito61].
The perverse (Leray) filtration is
 $$ \begin{align*} P_k IH^d(X)= \mathrm{Im} \bigg\{ H^d(\bigoplus^{k-r}_{i=-r} {}^{\mathfrak{p}}\mathcal{H}^i(Rf_*IC_X)[-i-\dim X])\to IH^d(X)\bigg\}. \end{align*} $$
$$ \begin{align*} P_k IH^d(X)= \mathrm{Im} \bigg\{ H^d(\bigoplus^{k-r}_{i=-r} {}^{\mathfrak{p}}\mathcal{H}^i(Rf_*IC_X)[-i-\dim X])\to IH^d(X)\bigg\}. \end{align*} $$
When Y is affine, de Cataldo and Migliorini provided a simple geometric characterisation of the perverse filtration; see [Reference de Cataldo and Migliorini20, Theorem 4.1.1]. Let
![]() $\Lambda ^s\subset Y$
be a general s-dimensional affine section of
$\Lambda ^s\subset Y$
be a general s-dimensional affine section of
![]() $Y\subset \mathbb {A}^N$
. Then
$Y\subset \mathbb {A}^N$
. Then
 $$ \begin{align} P_k IH^d(X) = \mathrm{Ker}\left\lbrace IH^d(X)\rightarrow IH^d(f^{-1}(\Lambda^{d-k-1})) \right \rbrace. \end{align} $$
$$ \begin{align} P_k IH^d(X) = \mathrm{Ker}\left\lbrace IH^d(X)\rightarrow IH^d(f^{-1}(\Lambda^{d-k-1})) \right \rbrace. \end{align} $$
This means that the cocycle
![]() $\eta \in IH^d(X)$
belongs to
$\eta \in IH^d(X)$
belongs to
![]() $P_kIH^d(X)$
if and only if its restriction to
$P_kIH^d(X)$
if and only if its restriction to
![]() $f^{-1}(\Lambda ^{d-k-1})$
vanishes; that is,
$f^{-1}(\Lambda ^{d-k-1})$
vanishes; that is,
![]() $\eta |_{f^{-1}(\Lambda ^{d-k-1})}=0$
.
$\eta |_{f^{-1}(\Lambda ^{d-k-1})}=0$
.
2.3 Mixed Hodge structure of semi-projective varieties
In order to compute the intersection Poincaré polynomial of M, we observe that
![]() ${M}_{\mathrm {Dol}}$
and
${M}_{\mathrm {Dol}}$
and
![]() ${T}_{\mathrm {Dol}}$
are semi-projective.
${T}_{\mathrm {Dol}}$
are semi-projective.
Definition 2.2. Reference Hausel and Rodriguez-Villegas34, Definition 1.1.1
A semiprojective variety is a complex quasi-projective variety X with a
![]() $\mathbb {G}_m$
-action such that
$\mathbb {G}_m$
-action such that
-
• the fixed point set
 $\operatorname {Fix}(X)$
is proper;
$\operatorname {Fix}(X)$
is proper; -
• for every
 $m \in X$
the limit
$m \in X$
the limit
 $\lim _{\lambda \to 0} \lambda \cdot m$
exists.
$\lim _{\lambda \to 0} \lambda \cdot m$
exists.
The core of X, denoted
![]() $\mathrm {Core}(X)$
, is the (proper) union of the repelling sets of
$\mathrm {Core}(X)$
, is the (proper) union of the repelling sets of
![]() $\operatorname {Fix}(X)$
; see [Reference Hausel and Rodriguez-Villegas34, Corollary 1.2.2].
$\operatorname {Fix}(X)$
; see [Reference Hausel and Rodriguez-Villegas34, Corollary 1.2.2].
Proposition 2.3. Let X be a semi-projective variety. Then the inclusion
![]() $\mathrm {Core}(X) \subset X$
is a homotopy equivalence.
$\mathrm {Core}(X) \subset X$
is a homotopy equivalence.
Proof. The flow
![]() $\mathbb {R}^+ \times X \to X$
, induced by the
$\mathbb {R}^+ \times X \to X$
, induced by the
![]() $\mathbb {G}_m$
-action, defines a deformation retract of X onto a neighbourhood of
$\mathbb {G}_m$
-action, defines a deformation retract of X onto a neighbourhood of
![]() $\mathrm {Core}(X)$
, which in turn is homotopy equivalent to
$\mathrm {Core}(X)$
, which in turn is homotopy equivalent to
![]() $\mathrm {Core}(X)$
.
$\mathrm {Core}(X)$
.
Proposition 2.4. If X is a semiprojective variety, then
-
1. the mixed Hodge structure on
 $IH^*(X)$
is pure;
$IH^*(X)$
is pure; -
2.
 $W_{d-1}H^d(X) = \ker \{ H^{d}(X) \to IH^{d}(X)\}$
, and
$W_{d-1}H^d(X) = \ker \{ H^{d}(X) \to IH^{d}(X)\}$
, and
 $W_d H^d(X) = H^d(X)$
.
$W_d H^d(X) = H^d(X)$
.
Proof. Let
![]() $f\colon \widetilde {X} \to X$
be a
$f\colon \widetilde {X} \to X$
be a
![]() $\mathbb {G}_m$
-equivariant resolution of singularities of X. Then
$\mathbb {G}_m$
-equivariant resolution of singularities of X. Then
![]() $\widetilde {X}$
is smooth and semiprojective, and it has pure cohomology by [Reference Hausel and Rodriguez-Villegas34, Corollary 1.3.2]. Via the decomposition theorem, the mixed Hodge structure on
$\widetilde {X}$
is smooth and semiprojective, and it has pure cohomology by [Reference Hausel and Rodriguez-Villegas34, Corollary 1.3.2]. Via the decomposition theorem, the mixed Hodge structure on
![]() $IH^*(X) \subset H^*(\tilde {X})$
is pure, too.
$IH^*(X) \subset H^*(\tilde {X})$
is pure, too.
As X retracts onto the proper algebraic variety
![]() $\mathrm {Core}(X)$
, the weight filtration on
$\mathrm {Core}(X)$
, the weight filtration on
![]() $H^*(X)\simeq H^*(\mathrm {Core}(X))$
is concentrated in degree
$H^*(X)\simeq H^*(\mathrm {Core}(X))$
is concentrated in degree
![]() $[0, 2d]$
by [Reference Peters and Steenbrink60, Theorem 5.39]; that is,
$[0, 2d]$
by [Reference Peters and Steenbrink60, Theorem 5.39]; that is,
![]() $W_d H^d(X) = H^d(X)$
.
$W_d H^d(X) = H^d(X)$
.
The resolution f induces a surjective morphism
 $\mathrm {Core}(\widetilde {X}) \to \mathrm {Core}(X)$
of proper algebraic varieties. Hence, by [Reference Peters and Steenbrink60, Corollary 5.43] we have
$\mathrm {Core}(\widetilde {X}) \to \mathrm {Core}(X)$
of proper algebraic varieties. Hence, by [Reference Peters and Steenbrink60, Corollary 5.43] we have
 $$ \begin{align*}W_{d-1}H^d(\mathrm{Core}(X)) = \ker \{f^*\colon H^d(\mathrm{Core}(X)) \to H^d(\mathrm{Core}(\tilde{X}))\},\end{align*} $$
$$ \begin{align*}W_{d-1}H^d(\mathrm{Core}(X)) = \ker \{f^*\colon H^d(\mathrm{Core}(X)) \to H^d(\mathrm{Core}(\tilde{X}))\},\end{align*} $$
and so
 $W_{d-1}H^d(X) = \ker \{ f^*\colon H^{d}(X) \to H^d(\widetilde {X})\}$
by Proposition 2.3. Finally, since
$W_{d-1}H^d(X) = \ker \{ f^*\colon H^{d}(X) \to H^d(\widetilde {X})\}$
by Proposition 2.3. Finally, since
![]() $f^*$
factors as
$f^*$
factors as
 $H^d(X) \to IH^d(X) \hookrightarrow H^d(\widetilde {X})$
, we conclude that
$H^d(X) \to IH^d(X) \hookrightarrow H^d(\widetilde {X})$
, we conclude that
The multiplicative group
![]() $\mathbb {G}_m$
acts on
$\mathbb {G}_m$
acts on
![]() ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
by
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
by
![]() $\lambda \cdot (E, \phi )=(E, \lambda \phi )$
. The Hitchin fibration
$\lambda \cdot (E, \phi )=(E, \lambda \phi )$
. The Hitchin fibration
 $$ \begin{align} \chi\colon {M}_{\mathrm{Dol}}(C, \operatorname{SL}_n) \to \bigoplus^{n}_{i=2} H^0(C, K_C^{\otimes i}) \end{align} $$
$$ \begin{align} \chi\colon {M}_{\mathrm{Dol}}(C, \operatorname{SL}_n) \to \bigoplus^{n}_{i=2} H^0(C, K_C^{\otimes i}) \end{align} $$
assigns to
![]() $(E, \phi )$
the characteristic polynomial of the Higgs field
$(E, \phi )$
the characteristic polynomial of the Higgs field
![]() $\phi $
. By [Reference Simpson66, Theorem 6.11] the map
$\phi $
. By [Reference Simpson66, Theorem 6.11] the map
![]() $\chi $
is a proper
$\chi $
is a proper
![]() $\mathbb {G}_m$
-equivariant map, where
$\mathbb {G}_m$
-equivariant map, where
![]() $\mathbb {G}_m$
acts linearly on
$\mathbb {G}_m$
acts linearly on
 $H^0(X, K_X^{\otimes i})$
with weight i. In particular,
$H^0(X, K_X^{\otimes i})$
with weight i. In particular,
![]() $\operatorname {Fix}({M}_{\mathrm {Dol}}(C, \operatorname {SL}_n))$
is contained in the nilpotent cone
$\operatorname {Fix}({M}_{\mathrm {Dol}}(C, \operatorname {SL}_n))$
is contained in the nilpotent cone
![]() $\chi ^{-1}(0)$
. Therefore,
$\chi ^{-1}(0)$
. Therefore,
![]() ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
is semiprojective.
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
is semiprojective.
The same argument works for
![]() $G=\operatorname {GL}_n, \operatorname {PGL}_n$
as well.
$G=\operatorname {GL}_n, \operatorname {PGL}_n$
as well.
2.4 Stable isosingularity principle
Let S be a smooth projective K3 surface or an abelian surface. In this section we establish a stable isosingularity principle for the (nonproper) Dolbeault moduli spaces
![]() $M(C, \operatorname {GL}_n)$
and
$M(C, \operatorname {GL}_n)$
and
![]() $M(C, \operatorname {SL}_n)$
and the (proper) Mukai moduli spaces
$M(C, \operatorname {SL}_n)$
and the (proper) Mukai moduli spaces
![]() $M(S, v)$
and
$M(S, v)$
and
![]() $K(S, v)$
. This means that these moduli spaces have the same analytic singularities, up to multiplication by a polydisk. The upshot is that
$K(S, v)$
. This means that these moduli spaces have the same analytic singularities, up to multiplication by a polydisk. The upshot is that
-
• the description of the local model of the singularities of
 $M(S,v)$
in [Reference O’Grady56] or [Reference Choy and Kiem8] holds for
$M(S,v)$
in [Reference O’Grady56] or [Reference Choy and Kiem8] holds for
 $M(C, \operatorname {GL}_2)$
and
$M(C, \operatorname {GL}_2)$
and
 $M(C, \operatorname {SL}_2)$
mutatis mutandis;
$M(C, \operatorname {SL}_2)$
mutatis mutandis; -
• the same sequence of blow-ups which desingularises
 $M(S,v)$
in [Reference O’Grady56] resolves the singularities of
$M(S,v)$
in [Reference O’Grady56] resolves the singularities of
 $M(C, \operatorname {GL}_2)$
and
$M(C, \operatorname {GL}_2)$
and
 $M(C, \operatorname {SL}_2)$
mutatis mutandis;
$M(C, \operatorname {SL}_2)$
mutatis mutandis; -
• the description of the summands of the decomposition theorem in Theorem 1.2 holds for
 $M(C, \operatorname {GL}_2)$
,
$M(C, \operatorname {GL}_2)$
,
 $M(C, \operatorname {SL}_2)$
,
$M(C, \operatorname {SL}_2)$
,
 $M(S, v)$
and
$M(S, v)$
and
 $K(S, v)$
with Mukai vector
$K(S, v)$
with Mukai vector
 $v = 2 w \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
, where w is primitive and
$v = 2 w \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
, where w is primitive and
 $w^2=2(g-1)$
.
$w^2=2(g-1)$
.
We briefly recall the definition of Mukai moduli space. Fix an effective Mukai vectorFootnote
2
![]() $v \in H^{*}_{\mathrm {alg}}(S, \mathbb {Z})$
. Define
$v \in H^{*}_{\mathrm {alg}}(S, \mathbb {Z})$
. Define
![]() $M(S, v)$
the moduli space of Gieseker H-semistable sheaves on S with Mukai vector v for a sufficiently general polarisation H (which we will typically omit in the notation); see [Reference Simpson65, §1]. Further, if S is an abelian variety with dual
$M(S, v)$
the moduli space of Gieseker H-semistable sheaves on S with Mukai vector v for a sufficiently general polarisation H (which we will typically omit in the notation); see [Reference Simpson65, §1]. Further, if S is an abelian variety with dual
![]() $\hat {S}$
, and
$\hat {S}$
, and
![]() $\dim M(S,v)\geq 6$
, then the Albanese morphism
$\dim M(S,v)\geq 6$
, then the Albanese morphism
 $\operatorname {alb}\colon M(S, v) \to S \times \hat {S}$
is isotrivial, and we set
$\operatorname {alb}\colon M(S, v) \to S \times \hat {S}$
is isotrivial, and we set
![]() $K(S, v) := \operatorname {alb}^{-1}(0_S, \mathcal {O}_S)$
.
$K(S, v) := \operatorname {alb}^{-1}(0_S, \mathcal {O}_S)$
.
Remark 2.5 Donagi–Ein–Lazarsfeld degeneration
Mukai moduli spaces should be thought of as locally trivial deformations of Dolbeault moduli spaces as follows. Fix an ample curve
![]() $C \subset S$
of genus
$C \subset S$
of genus
![]() $g \geq 2$
. Donagi, Ein and Lazarsfeld showed in [Reference Donagi, Ein and Lazarsfeld22] that there exists a flat family
$g \geq 2$
. Donagi, Ein and Lazarsfeld showed in [Reference Donagi, Ein and Lazarsfeld22] that there exists a flat family
![]() $\pi _{\mathcal {W}}\colon \mathcal {W} \to \mathbb {P}^1$
such that
$\pi _{\mathcal {W}}\colon \mathcal {W} \to \mathbb {P}^1$
such that
-
1.
 $\pi _{\mathcal {W}}^{-1}(\mathbb {P}^1 \setminus \{0\}) \simeq M(S,(0, nC, -n C^2/2)) \times \mathbb {A}^1$
;
$\pi _{\mathcal {W}}^{-1}(\mathbb {P}^1 \setminus \{0\}) \simeq M(S,(0, nC, -n C^2/2)) \times \mathbb {A}^1$
; -
2.
 $\pi _{\mathcal {W}}^{-1}(0)\simeq {M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
.
$\pi _{\mathcal {W}}^{-1}(0)\simeq {M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
.
Unless
![]() $g=2$
and
$g=2$
and
![]() $n=2$
,
$n=2$
,
![]() $M(S,(0, nC, -n C^2/2))$
and
$M(S,(0, nC, -n C^2/2))$
and
![]() ${M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
have
${M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
have
![]() $\mathbb {Q}$
-factorial terminal symplectic singularities; see [Reference Kaledin, Lehn and Sorger39, Theorem B] and [Reference Bellamy and Schedler6, Theorem 1.2], together with Simpson’s isosingularity principle [Reference Simpson66, Theorem 10.6]. Hence, by [Reference Namikawa55, Theorem 17] the morphism
$\mathbb {Q}$
-factorial terminal symplectic singularities; see [Reference Kaledin, Lehn and Sorger39, Theorem B] and [Reference Bellamy and Schedler6, Theorem 1.2], together with Simpson’s isosingularity principle [Reference Simpson66, Theorem 10.6]. Hence, by [Reference Namikawa55, Theorem 17] the morphism
![]() $\pi _{\mathcal {W}}$
is locally analytically trivial.Footnote
3
Roughly, this means that the two moduli spaces have the same singularities. We make this statement precise in Proposition 2.10.
$\pi _{\mathcal {W}}$
is locally analytically trivial.Footnote
3
Roughly, this means that the two moduli spaces have the same singularities. We make this statement precise in Proposition 2.10.
We start by stating the notion of stable isosingularity.
Definition 2.6. Two varieties X and Y are stably isosingular if there exist complex Whitney stratificationsFootnote
4
by (smooth nonnecessarily connected) locally Zariski-closed subsets
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
such that
$Y_i$
such that
-
1.
 $X = \bigsqcup _i X_i$
and
$X = \bigsqcup _i X_i$
and
 $Y = \bigsqcup _i Y_i$
;
$Y = \bigsqcup _i Y_i$
; -
2. the posets of closed subsets
 $\{\overline {X}_i\}$
and
$\{\overline {X}_i\}$
and
 $\{\overline {Y}_i\}$
ordered by inclusion are equal;
$\{\overline {Y}_i\}$
ordered by inclusion are equal; -
3. the normal slices through
 $X_i$
and
$X_i$
and
 $Y_i$
are locally analytically isomorphic.
$Y_i$
are locally analytically isomorphic.
If
![]() $\dim X= \dim Y$
, then we say that X and Y are isosingular.
$\dim X= \dim Y$
, then we say that X and Y are isosingular.
It is implicit in
3. that the stratifications above are analytically equisingular along each stratum; that is, the analytic type of the normal slices through
![]() $x \in X_i$
(respectively
$x \in X_i$
(respectively
![]() $y \in Y_i$
) is independent of x (respectively y). Not all algebraic variety admits such a stratification; see [Reference Whitney68, Example 13.1]. However, the moduli spaces considered below will satisfy the following stronger condition of analytic normal triviality.
$y \in Y_i$
) is independent of x (respectively y). Not all algebraic variety admits such a stratification; see [Reference Whitney68, Example 13.1]. However, the moduli spaces considered below will satisfy the following stronger condition of analytic normal triviality.
Definition 2.7. A Whitney stratification
![]() $X = \bigsqcup _i X_i$
is analytically trivial in the normal direction to each strata, if for any
$X = \bigsqcup _i X_i$
is analytically trivial in the normal direction to each strata, if for any
![]() $x \in X_i$
there exists a normal slice
$x \in X_i$
there exists a normal slice
![]() $N_x$
through
$N_x$
through
![]() $X_i$
at x, and a neighbourhood of x in X which is locally analytically isomorphic to
$X_i$
at x, and a neighbourhood of x in X which is locally analytically isomorphic to
![]() $N_x \times T_x X_i$
at
$N_x \times T_x X_i$
at
![]() $(x, 0)$
.
$(x, 0)$
.
Note that if X and Y are stably isosingular via Whitney stratifications which are analytically trivial in the normal direction and a sequence of blow-ups along (the strict transforms of) some
![]() $X_i$
gives a desingularisation of X, then the same sequence of blow-ups along the corresponding strata
$X_i$
gives a desingularisation of X, then the same sequence of blow-ups along the corresponding strata
![]() $Y_i$
gives a desingularisation of Y. In addition, if X and Y are isosingular, then an analytic neighbourhood of any point of X is isomorphic to an analytic neighbourhood of some point in Y.
$Y_i$
gives a desingularisation of Y. In addition, if X and Y are isosingular, then an analytic neighbourhood of any point of X is isomorphic to an analytic neighbourhood of some point in Y.
Example 2.8 Analytically trivial fibrations
Let
![]() $f\colon X \to Y$
be an analytic locally trivial fibration, and suppose that
$f\colon X \to Y$
be an analytic locally trivial fibration, and suppose that
![]() $F := f^{-1}(y)$
, with
$F := f^{-1}(y)$
, with
![]() $y \in Y$
, admits an analytically equisingular Whitney stratification. Then X and F are stably isosingular. Indeed, by the local triviality, any Whitney stratification of
$y \in Y$
, admits an analytically equisingular Whitney stratification. Then X and F are stably isosingular. Indeed, by the local triviality, any Whitney stratification of
![]() $f^{-1}(y)$
can be lifted to a Whitney stratification on X with the same normal slices. In particular, if W is a smooth algebraic variety, F and
$f^{-1}(y)$
can be lifted to a Whitney stratification on X with the same normal slices. In particular, if W is a smooth algebraic variety, F and
![]() $F \times W$
are stably isosingular.
$F \times W$
are stably isosingular.
Lemma 2.9 Quadraticity of deformation spaces
Let
![]() $[F] \in M_{\mathrm {B}}(C, \operatorname {GL}_n)$
or
$[F] \in M_{\mathrm {B}}(C, \operatorname {GL}_n)$
or
![]() $M(S,v)$
be a singular point corresponding to the polystable representation or polystable sheaf F. Then the representation space
$M(S,v)$
be a singular point corresponding to the polystable representation or polystable sheaf F. Then the representation space
![]() $\operatorname {Hom}(\pi _1(C), \operatorname {GL}_n)$
at F or the deformation space
$\operatorname {Hom}(\pi _1(C), \operatorname {GL}_n)$
at F or the deformation space
![]() $\mathrm {Def}_F$
(cf. [Reference Huybrechts and Lehn38, §2.A.6]) is quadratic; that is, it is locally isomorphic to a (reduced) complete intersection of homogeneous quadrics.
$\mathrm {Def}_F$
(cf. [Reference Huybrechts and Lehn38, §2.A.6]) is quadratic; that is, it is locally isomorphic to a (reduced) complete intersection of homogeneous quadrics.
Proof. This follows from the Goldaman-Millson theory [Reference Goldman and Millson28] if
![]() $[F] \in M_{\mathrm {B}}(C, \operatorname {GL}_n)$
or [Reference Arbarello and Saccà2, Theorem 1.2] if
$[F] \in M_{\mathrm {B}}(C, \operatorname {GL}_n)$
or [Reference Arbarello and Saccà2, Theorem 1.2] if
![]() $[F] \in M(S,v)$
, with S K3 surface. Looking into the proof of [Reference Arbarello and Saccà2, Theorem 3.7 and 3.8] and [Reference Zhang69], one can see that the same proof holds for
$[F] \in M(S,v)$
, with S K3 surface. Looking into the proof of [Reference Arbarello and Saccà2, Theorem 3.7 and 3.8] and [Reference Zhang69], one can see that the same proof holds for
![]() $[F] \in M(S,v)$
with S abelian surface.
$[F] \in M(S,v)$
with S abelian surface.
Proposition 2.10. Let S be a K3 or an abelian surface with
![]() $\operatorname {Pic}(S)\simeq \mathbb {Z}$
generated by the class of a curve C of genus
$\operatorname {Pic}(S)\simeq \mathbb {Z}$
generated by the class of a curve C of genus
![]() $g \geq 2$
. Then
$g \geq 2$
. Then
![]() $M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
$M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
![]() $M(S,(0, nC, -nC^2/2))$
are isosingular.
$M(S,(0, nC, -nC^2/2))$
are isosingular.
Proof. Given a (quasi-projective) variety X equipped with the action of a reductive group G, let
![]() be the quotient map. Any fibre
be the quotient map. Any fibre
![]() $\xi ^{-1}(y)$
, with
$\xi ^{-1}(y)$
, with
![]() $y \in Y$
, contains a closed G-orbit
$y \in Y$
, contains a closed G-orbit
![]() $T(y)$
. Denote the conjugacy class of a closed subgroup H of G by
$T(y)$
. Denote the conjugacy class of a closed subgroup H of G by
![]() $(H)$
. Then
$(H)$
. Then
![]() $Y_{(H)}$
is the set of points
$Y_{(H)}$
is the set of points
![]() $y \in Y$
such that the stabiliser of
$y \in Y$
such that the stabiliser of
![]() $x \in T(y)$
is in
$x \in T(y)$
is in
![]() $(H)$
. The loci
$(H)$
. The loci
![]() $Y_{(H)}$
are the strata of the stratification by orbit type of Y.
$Y_{(H)}$
are the strata of the stratification by orbit type of Y.
If Y is a Nakajima quiver variety,Footnote 5 then the stratification by orbit type is a complex Whitney stratification, which is analytically trivial in the normal direction to each stratum, due to [Reference Mayrand50, Proposition 4.2].
![]() $M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
$M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
![]() $M(S,(0, nC, -nC^2/2))$
are
$M(S,(0, nC, -nC^2/2))$
are
![]() $\operatorname {PGL}_N$
-quotients, and the quadraticity of the deformation spaces implies that they are locally modelled on Nakajima quiver varieties; see [Reference Bellamy and Schedler6, Theorem 2.5] and [Reference Arbarello and Saccà2, Proposition 6.1]. By construction, the stratifications by orbit type of
$\operatorname {PGL}_N$
-quotients, and the quadraticity of the deformation spaces implies that they are locally modelled on Nakajima quiver varieties; see [Reference Bellamy and Schedler6, Theorem 2.5] and [Reference Arbarello and Saccà2, Proposition 6.1]. By construction, the stratifications by orbit type of
![]() $M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
$M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
![]() $M(S,(0, nC, -nC^2/2))$
are locally isomorphic to stratification by orbit type of quiver varieties, and so they are complex Whitney stratifications, analytically trivial in the normal direction to each stratum.
$M(S,(0, nC, -nC^2/2))$
are locally isomorphic to stratification by orbit type of quiver varieties, and so they are complex Whitney stratifications, analytically trivial in the normal direction to each stratum.
A singular point of either moduli space is a polystable objects
 $$ \begin{align*}F = F^{l_1}_1\oplus \ldots \oplus F^{l_s}_s,\end{align*} $$
$$ \begin{align*}F = F^{l_1}_1\oplus \ldots \oplus F^{l_s}_s,\end{align*} $$
where
![]() $F_i$
are distinct stable factors. The automorphism group of F is
$F_i$
are distinct stable factors. The automorphism group of F is
 $$ \begin{align*}\prod^s_{i=1} \operatorname{GL}_{l_i} \subset \operatorname{GL}_n,\end{align*} $$
$$ \begin{align*}\prod^s_{i=1} \operatorname{GL}_{l_i} \subset \operatorname{GL}_n,\end{align*} $$
which can be identified up to constants with the stabiliser of a point in
![]() $T(F)$
under the
$T(F)$
under the
![]() $\operatorname {PGL}_N$
-action; see, for instance, [Reference Kaledin, Lehn and Sorger39, §2.5].Footnote
6
$\operatorname {PGL}_N$
-action; see, for instance, [Reference Kaledin, Lehn and Sorger39, §2.5].Footnote
6
The poset of inclusions of the orbit type strata for both the Dolbeault and Mukai moduli spaces is isomorphic to the poset of inclusion of the stabilisers of
![]() $T(F)$
, and the analytic type of the normal slice through an orbit type strata is prescribed by the (abstract) isomorphism class of the stabiliser; see again [Reference Bellamy and Schedler6, Theorem 2.5] and [Reference Kaledin, Lehn and Sorger39, §2.7]. This gives
2
. and
3
. of Definition 2.6. The isosingularity follows from
$T(F)$
, and the analytic type of the normal slice through an orbit type strata is prescribed by the (abstract) isomorphism class of the stabiliser; see again [Reference Bellamy and Schedler6, Theorem 2.5] and [Reference Kaledin, Lehn and Sorger39, §2.7]. This gives
2
. and
3
. of Definition 2.6. The isosingularity follows from
There exists a clear geometric argument for Proposition 2.10, sketched below.
Proof Sketch of the proof of Proposition 2.10 via a degeneration argument
Via the Donagi–Ein–Lazarsfeld degeneration one can actually prove that
![]() ${M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
is isosingular to a neighbourhood of a nilpotent cone of
${M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
is isosingular to a neighbourhood of a nilpotent cone of
![]() $M(S,(0, nC, -nC^2/2))$
as defined in [Reference Donagi, Ein and Lazarsfeld22, §2]. This is an analytic open set of the Mukai moduli space that intersects all of the orbit type strata, if C generates the Picard group of S. In order to extend the result to the whole Mukai moduli space, it is sufficient to invoke the analytic triviality in the normal direction of the stratification by orbit type of
$M(S,(0, nC, -nC^2/2))$
as defined in [Reference Donagi, Ein and Lazarsfeld22, §2]. This is an analytic open set of the Mukai moduli space that intersects all of the orbit type strata, if C generates the Picard group of S. In order to extend the result to the whole Mukai moduli space, it is sufficient to invoke the analytic triviality in the normal direction of the stratification by orbit type of
![]() $M(S,(0, nC, -nC^2/2))$
, which follows from the quadraticity of the deformation spaces Lemma 2.9.
$M(S,(0, nC, -nC^2/2))$
, which follows from the quadraticity of the deformation spaces Lemma 2.9.
Theorem 2.11 Stable isosingularity principle
Let C be a curve of genus
![]() $g \geq 2$
, and let S be a K3 or an abelian surface. Fix a Mukai vector
$g \geq 2$
, and let S be a K3 or an abelian surface. Fix a Mukai vector
![]() $v = n w \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
, where w is primitive and
$v = n w \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
, where w is primitive and
![]() $w^2=2(g-1)$
.
$w^2=2(g-1)$
.
Then
![]() $M(C, \operatorname {GL}_n)$
,
$M(C, \operatorname {GL}_n)$
,
![]() $M(C, \operatorname {SL}_n)$
,
$M(C, \operatorname {SL}_n)$
,
![]() $M(S, v)$
and
$M(S, v)$
and
![]() $K(S, v)$
are stably isosingular.
$K(S, v)$
are stably isosingular.
Proof.
-
•
 ${M}_{\mathrm {Dol}}(C,G)$
and
${M}_{\mathrm {Dol}}(C,G)$
and
 ${M}_{\mathrm {B}}(C,G)$
are isosingular by [Reference Simpson66, Theorem 10.6], independently on the complex structure of C.
${M}_{\mathrm {B}}(C,G)$
are isosingular by [Reference Simpson66, Theorem 10.6], independently on the complex structure of C. -
• Now let
 $S'$
be a K3 or an abelian surface such that C embeds in
$S'$
be a K3 or an abelian surface such that C embeds in
 $S'$
and generates its Picard group. Then
$S'$
and generates its Picard group. Then
 $M(S',(0, nC, -nC^2/2))$
and
$M(S',(0, nC, -nC^2/2))$
and
 $M(S,v)$
(respectively
$M(S,v)$
(respectively
 $K(S',(0, nC, -nC^2/2))$
and
$K(S',(0, nC, -nC^2/2))$
and
 $K(S,v)$
) are isosingular by [Reference Perego and Rapagnetta59, Theorem 1.17], independently on the complex structure of S.
$K(S,v)$
) are isosingular by [Reference Perego and Rapagnetta59, Theorem 1.17], independently on the complex structure of S. -
•
 $M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
$M_{\mathrm {B}}(C, \operatorname {GL}_n)$
and
 $M(S',(0, nC, -nC^2/2))$
are isosingular by Proposition 2.10.
$M(S',(0, nC, -nC^2/2))$
are isosingular by Proposition 2.10. -
• Let S be an abelian surface. The morphisms
 $\operatorname {alb}\colon M(S, v) \to S \times \hat {S}$
and
$\operatorname {alb}\colon M(S, v) \to S \times \hat {S}$
and
 $\operatorname {alb}\colon {M}_{\mathrm {Dol}}(C, \operatorname {GL}_n) \to M(C, \operatorname {GL}_1)$
, given by
$\operatorname {alb}\colon {M}_{\mathrm {Dol}}(C, \operatorname {GL}_n) \to M(C, \operatorname {GL}_1)$
, given by
 $\operatorname {alb}((E, \phi ))=(\det E, \text {tr} \phi )$
, are étale locally trivial fibrations with fibers
$\operatorname {alb}((E, \phi ))=(\det E, \text {tr} \phi )$
, are étale locally trivial fibrations with fibers
 ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
and
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
and
 $K(S, v)$
, respectively. The restriction of
$K(S, v)$
, respectively. The restriction of
 $\operatorname {alb}$
to the orbit type strata is étale locally trivial, too. This means that there exists a neighbourhood of
$\operatorname {alb}$
to the orbit type strata is étale locally trivial, too. This means that there exists a neighbourhood of
 $[F] \in M(S,v)_{(H)}$
locally analytically isomorphic to (12)at
$[F] \in M(S,v)_{(H)}$
locally analytically isomorphic to (12)at $$ \begin{align} N_{[F]} \times T_{[F]}M(S,v)_{(H)} \simeq N_{[F]} \times T_{[F]}K(S, v)_{(H)} \times T_{\operatorname{alb}([F])}(S \times \hat{S}) \end{align} $$
$$ \begin{align} N_{[F]} \times T_{[F]}M(S,v)_{(H)} \simeq N_{[F]} \times T_{[F]}K(S, v)_{(H)} \times T_{\operatorname{alb}([F])}(S \times \hat{S}) \end{align} $$
 $([F], 0)$
, where
$([F], 0)$
, where
 $N_{[F]}$
is a normal slice through
$N_{[F]}$
is a normal slice through
 $K(S, v)_{(H)}$
at
$K(S, v)_{(H)}$
at
 $[F]$
. Further, the morphism
$[F]$
. Further, the morphism
 $\operatorname {alb}$
is locally given by the linear projection onto the last factor of (12) by Lemma 2.9. The same argument works for
$\operatorname {alb}$
is locally given by the linear projection onto the last factor of (12) by Lemma 2.9. The same argument works for
 ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
, too. As in Example 2.8, we conclude that
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
, too. As in Example 2.8, we conclude that
 ${M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
and
${M}_{\mathrm {Dol}}(C, \operatorname {GL}_n)$
and
 ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
(respectively
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_n)$
(respectively
 $M(S, v)$
and
$M(S, v)$
and
 $K(S, v)$
) are stably isosingular.
$K(S, v)$
) are stably isosingular.
3 Kirwan–O’Grady desingularisation
3.1 Singularities of M
Recall that M denotes indifferently the moduli spaces
![]() ${M}_{\mathrm {B}}(C,G)$
or
${M}_{\mathrm {B}}(C,G)$
or
![]() ${M}_{\mathrm {Dol}}(C,G)$
with
${M}_{\mathrm {Dol}}(C,G)$
with
![]() $G=\operatorname {GL}_2$
or
$G=\operatorname {GL}_2$
or
![]() $\operatorname {SL}_2$
. The stratification by orbit type of M (cf. Subsection 2.4) determines a filtration by closed subsets
$\operatorname {SL}_2$
. The stratification by orbit type of M (cf. Subsection 2.4) determines a filtration by closed subsets
In this section we characterise
![]() $\Sigma $
,
$\Sigma $
,
![]() $\Omega $
and their normal slices, mainly appealing to [Reference O’Grady56].
$\Omega $
and their normal slices, mainly appealing to [Reference O’Grady56].
Proposition 3.1.
-
1.
 $M(C, G)$
is an algebraic variety of dimension
$M(C, G)$
is an algebraic variety of dimension
 $6g-6$
if
$6g-6$
if
 $G=\operatorname {SL}_2$
or
$G=\operatorname {SL}_2$
or
 $8g-6$
if
$8g-6$
if
 $G=\operatorname {GL}_2$
.
$G=\operatorname {GL}_2$
. -
2. The singular locus of M is the subvariety of strictly semi-simple Higgs bundles or representations.
-
3. If
 $g \geq 3$
, M is factorial with terminal symplectic singularities. If
$g \geq 3$
, M is factorial with terminal symplectic singularities. If
 $g=2$
, M admits a symplectic resolution.
$g=2$
, M admits a symplectic resolution.
Proof. The statements have been proved for
![]() $M_{\mathrm {B}}(C, \operatorname {GL}_2)$
in [Reference Bellamy and Schedler6, Theorem 1.1, 1.2, 1.5, Lemma 2.8]. The same holds for M by the stable isosingularity principle (Theorem 2.11), possibly with the exception of the factoriality. However, to show that M is factorial, one can repeat the argument of [Reference Bellamy and Schedler6, Theorem 1.2] word for word.
$M_{\mathrm {B}}(C, \operatorname {GL}_2)$
in [Reference Bellamy and Schedler6, Theorem 1.1, 1.2, 1.5, Lemma 2.8]. The same holds for M by the stable isosingularity principle (Theorem 2.11), possibly with the exception of the factoriality. However, to show that M is factorial, one can repeat the argument of [Reference Bellamy and Schedler6, Theorem 1.2] word for word.
Proposition 3.2 Singularities of M
-
1. The singular locus of
 $M_{\mathrm {B}} (C, \operatorname {SL}_2)$
, denoted
$M_{\mathrm {B}} (C, \operatorname {SL}_2)$
, denoted
 $\Sigma _{\mathrm {B}} (C, \operatorname {SL}_2)$
, is where
$\Sigma _{\mathrm {B}} (C, \operatorname {SL}_2)$
, is where
 $\mathbb {C}^* \subset \operatorname {SL}_2$
is the torus of diagonal matrices, and
$\mathbb {C}^* \subset \operatorname {SL}_2$
is the torus of diagonal matrices, and
 $\mathbb {Z}/2\mathbb {Z}$
acts on
$\mathbb {Z}/2\mathbb {Z}$
acts on
 $(\mathbb {C}^*)^{2g}$
by
$(\mathbb {C}^*)^{2g}$
by
 $v \mapsto v^{-1}$
. Set
$v \mapsto v^{-1}$
. Set
 $\Sigma _{\iota , \mathrm {B}} (C, \operatorname {SL}_2) := (\mathbb {C}^*)^{2g}$
.
$\Sigma _{\iota , \mathrm {B}} (C, \operatorname {SL}_2) := (\mathbb {C}^*)^{2g}$
.
-
2. The singular locus of
 $M_{\mathrm {B}} (C, \operatorname {GL}_2)$
, denoted
$M_{\mathrm {B}} (C, \operatorname {GL}_2)$
, denoted
 $\Sigma _{\mathrm {B}} (C, \operatorname {GL}_2)$
, is which is isomorphic to the second symmetric product of
$\Sigma _{\mathrm {B}} (C, \operatorname {GL}_2)$
, is which is isomorphic to the second symmetric product of
 $(\mathbb {C}^*)^{2g}$
. Set
$(\mathbb {C}^*)^{2g}$
. Set
 $\Sigma _{\iota , B} (C, \operatorname {GL}_2) := (\mathbb {C}^*)^{2g} \times (\mathbb {C}^*)^{2g}$
.
$\Sigma _{\iota , B} (C, \operatorname {GL}_2) := (\mathbb {C}^*)^{2g} \times (\mathbb {C}^*)^{2g}$
.
-
3. The singular locus of
 ${M}_{\mathrm {Dol}} (C, \operatorname {SL}_2)$
, denoted
${M}_{\mathrm {Dol}} (C, \operatorname {SL}_2)$
, denoted
 $\Sigma _{\mathrm {Dol}} (C, \operatorname {SL}_2)$
, is which is isomorphic to
$\Sigma _{\mathrm {Dol}} (C, \operatorname {SL}_2)$
, is which is isomorphic to $$ \begin{align*}\lbrace (E, \Phi) | \, (E, \Phi) \simeq (L, \phi) \oplus (L^{-1}, -\phi), \, L \in \operatorname{Jac}(C), \, \phi \in H^0(C, K_C) \rbrace,\end{align*} $$
where
$$ \begin{align*}\lbrace (E, \Phi) | \, (E, \Phi) \simeq (L, \phi) \oplus (L^{-1}, -\phi), \, L \in \operatorname{Jac}(C), \, \phi \in H^0(C, K_C) \rbrace,\end{align*} $$
where $$ \begin{align*}(\operatorname{Jac}(C) \times H^0(C, K_C))/(\mathbb{Z}/2\mathbb{Z}) \simeq T^*\operatorname{Jac}(C)/(\mathbb{Z}/2\mathbb{Z}),\end{align*} $$
$$ \begin{align*}(\operatorname{Jac}(C) \times H^0(C, K_C))/(\mathbb{Z}/2\mathbb{Z}) \simeq T^*\operatorname{Jac}(C)/(\mathbb{Z}/2\mathbb{Z}),\end{align*} $$
 $\mathbb {Z}/2\mathbb {Z}$
acts on
$\mathbb {Z}/2\mathbb {Z}$
acts on
 $\operatorname {Jac}(C)$
by
$\operatorname {Jac}(C)$
by
 $L \mapsto L^{-1}$
and on
$L \mapsto L^{-1}$
and on
 $H^0(C, K_C)$
by
$H^0(C, K_C)$
by
 $\phi \mapsto - \phi $
. Set
$\phi \mapsto - \phi $
. Set
 $\Sigma _{\iota , Dol} (C, \operatorname {SL}_2) := T^*\operatorname {Jac}(C)$
.
$\Sigma _{\iota , Dol} (C, \operatorname {SL}_2) := T^*\operatorname {Jac}(C)$
.
-
4. The singular locus of
 ${M}_{\mathrm {Dol}} (C, \operatorname {GL}_2)$
, denoted
${M}_{\mathrm {Dol}} (C, \operatorname {GL}_2)$
, denoted
 $\Sigma _{\mathrm {Dol}} (C, \operatorname {GL}_2)$
, is which is isomorphic to the second symmetric product of
$\Sigma _{\mathrm {Dol}} (C, \operatorname {GL}_2)$
, is which is isomorphic to the second symmetric product of $$ \begin{align*}\lbrace (E, \Phi) | \, (E, \Phi) \simeq (L, \phi) \oplus (L', \phi'), \, L, L' \in \operatorname{Jac}(C), \, \phi, \phi' \in H^0(C, K_C) \rbrace,\end{align*} $$
$$ \begin{align*}\lbrace (E, \Phi) | \, (E, \Phi) \simeq (L, \phi) \oplus (L', \phi'), \, L, L' \in \operatorname{Jac}(C), \, \phi, \phi' \in H^0(C, K_C) \rbrace,\end{align*} $$
 $T^*\operatorname {Jac}(C)$
. Set
$T^*\operatorname {Jac}(C)$
. Set
 $\Sigma _{\iota , Dol} (C, \operatorname {GL}_2) := T^*\operatorname {Jac}(C) \times T^*\operatorname {Jac}(C)$
.
$\Sigma _{\iota , Dol} (C, \operatorname {GL}_2) := T^*\operatorname {Jac}(C) \times T^*\operatorname {Jac}(C)$
.
-
5. The singular locus of
 $\Sigma (C, \operatorname {SL}_2)$
, denoted
$\Sigma (C, \operatorname {SL}_2)$
, denoted
 $\Omega (C, \operatorname {SL}_2)$
, is a set of
$\Omega (C, \operatorname {SL}_2)$
, is a set of
 $2^{2g}$
points.
$2^{2g}$
points. -
6. The singular locus of
 $\Sigma (C, \operatorname {GL}_2)$
, denoted
$\Sigma (C, \operatorname {GL}_2)$
, denoted
 $\Omega (C, \operatorname {GL}_2)$
, is isomorphic to
$\Omega (C, \operatorname {GL}_2)$
, is isomorphic to
 $M(C, \operatorname {GL}_1)$
.
$M(C, \operatorname {GL}_1)$
.
Proof. The result follows easily from Proposition 3.1.(2).
Definition 3.3.
-
1. By Proposition 3.2, there exists a double cover
 $q\colon \Sigma _{\iota } \to \Sigma $
branched along
$q\colon \Sigma _{\iota } \to \Sigma $
branched along
 $\Omega $
.
$\Omega $
. -
2. The involution
 $\iota \colon \Sigma _{\iota } \to \Sigma _{\iota }$
is the deck transformation of q.
$\iota \colon \Sigma _{\iota } \to \Sigma _{\iota }$
is the deck transformation of q. -
3. The largest open subset of
 $\Sigma _{\iota }$
where q is étale is denoted
$\Sigma _{\iota }$
where q is étale is denoted
 $\Sigma ^{\circ }_{\iota } := q^{-1}(\Sigma \setminus \Omega )$
.
$\Sigma ^{\circ }_{\iota } := q^{-1}(\Sigma \setminus \Omega )$
. -
4. There exists a rank-1 local system
 $\mathscr {L}$
on
$\mathscr {L}$
on
 $\Sigma ^{\circ } := \Sigma \setminus \Omega $
such that
$\Sigma ^{\circ } := \Sigma \setminus \Omega $
such that  $$ \begin{align*}q_* \mathbb{Q}_{\Sigma^{\circ}_{\iota}} = \mathbb{Q}_{\Sigma^{\circ}} \oplus \mathscr{L}.\end{align*} $$
$$ \begin{align*}q_* \mathbb{Q}_{\Sigma^{\circ}_{\iota}} = \mathbb{Q}_{\Sigma^{\circ}} \oplus \mathscr{L}.\end{align*} $$
Proposition 3.4 Normal slices
-
1. A slice
 $N_{\Sigma }$
normal to
$N_{\Sigma }$
normal to
 $\Sigma $
at a point in
$\Sigma $
at a point in
 $\Sigma \setminus \Omega $
is locally analytically isomorphic to an affine cone over the incidence variety with conormal bundle
$\Sigma \setminus \Omega $
is locally analytically isomorphic to an affine cone over the incidence variety with conormal bundle $$ \begin{align*}I_{2g-3} := \bigg\lbrace ([x_i], [y_j]) \in \mathbb{P}^{2g-3} \times \mathbb{P}^{2g-3} \, \big| \, \sum^{2g-3}_{k=0} x_k y_k =0\bigg\rbrace\end{align*} $$
$$ \begin{align*}I_{2g-3} := \bigg\lbrace ([x_i], [y_j]) \in \mathbb{P}^{2g-3} \times \mathbb{P}^{2g-3} \, \big| \, \sum^{2g-3}_{k=0} x_k y_k =0\bigg\rbrace\end{align*} $$
 $\mathcal {O}(1,1) := (\mathcal {O}_{\mathbb {P}^{2g-3}}(1) \boxtimes \mathcal {O}_{\mathbb {P}^{2g-3}}(1))|_{I_{2g-3}}$
.
$\mathcal {O}(1,1) := (\mathcal {O}_{\mathbb {P}^{2g-3}}(1) \boxtimes \mathcal {O}_{\mathbb {P}^{2g-3}}(1))|_{I_{2g-3}}$
.
-
2. Let
 $(W, q)$
be a vector space of dimension
$(W, q)$
be a vector space of dimension
 $3$
endowed with a quadratic form q of maximal rank and
$3$
endowed with a quadratic form q of maximal rank and
 $(V, \omega )$
be a symplectic vector space of dimension
$(V, \omega )$
be a symplectic vector space of dimension
 $2g$
. Let
$2g$
. Let
 $\operatorname {Hom}^{\omega }(W, V)$
be the cone of linear maps from W to V whose image is isotropic. Note that the group
$\operatorname {Hom}^{\omega }(W, V)$
be the cone of linear maps from W to V whose image is isotropic. Note that the group
 $SO(W)$
acts on
$SO(W)$
acts on
 $\operatorname {Hom}^{\omega }(W, V)$
by precomposition.
$\operatorname {Hom}^{\omega }(W, V)$
by precomposition.Then a normal slice
 $N_{\Omega }$
through
$N_{\Omega }$
through
 $\Omega $
is isomorphic to an affine cone over
$\Omega $
is isomorphic to an affine cone over
 .
.
Proof. The local models have been described in [Reference O’Grady56, (3.3.2)] (see also [Reference Choy and Kiem8, Proposition 3.2.(2)]) and in [Reference O’Grady56, (1.5.1)] (together with Lemma 2.9) for
![]() $M(S,v)$
with
$M(S,v)$
with
![]() $v=(2,0,-2c)$
. The description holds for M, too, by the stable isosingularity principle (Theorem 2.11).
$v=(2,0,-2c)$
. The description holds for M, too, by the stable isosingularity principle (Theorem 2.11).
3.2 Geometry of the desingularisation
Inspired by [Reference Kirwan42], O’Grady exhibits a desingularisation of the Mukai moduli spaces
![]() $M(S,v)$
of semistable sheaves on a projective K3 surface S with Mukai vector
$M(S,v)$
of semistable sheaves on a projective K3 surface S with Mukai vector
![]() $v=(2,0,-2c) \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
. By the stable isosingularity principle (cf. Subsection 2.4), the same sequence of blow-ups gives a desingularisation of M. In this section, we recall the geometry of the exceptional locus, and we compute the E-polynomials of its strata.
$v=(2,0,-2c) \in H^*_{\mathrm {alg}}(S, \mathbb {Z})$
. By the stable isosingularity principle (cf. Subsection 2.4), the same sequence of blow-ups gives a desingularisation of M. In this section, we recall the geometry of the exceptional locus, and we compute the E-polynomials of its strata.
Proposition 3.5 Kirwan–O’Grady desingularisation
Let
-
•
 $\pi _R \colon R \to M$
be the blow-up of M along
$\pi _R \colon R \to M$
be the blow-up of M along
 $\Omega $
;
$\Omega $
; -
•
 $\pi _S \colon S \to R$
be the blow-up of R along
$\pi _S \colon S \to R$
be the blow-up of R along
 $\Sigma _R := \pi ^{-1}_{R, *} \Sigma $
;
$\Sigma _R := \pi ^{-1}_{R, *} \Sigma $
; -
•
 $\pi _T \colon T \to S$
be the blow-up of S along its singular locus.
$\pi _T \colon T \to S$
be the blow-up of S along its singular locus.
Then the composition
![]() $\pi := \pi _R \circ \pi _S \circ \pi _T\colon T \to M$
is a log resolution of M.Footnote
7
$\pi := \pi _R \circ \pi _S \circ \pi _T\colon T \to M$
is a log resolution of M.Footnote
7
Proof. It follows from [Reference O’Grady56, 1.8.3] and Theorem 2.11.
Notation 3.6.
-
•
 $D_1$
,
$D_1$
,
 $D_2$
and
$D_2$
and
 $D_3$
are (the strict transform of) the exceptional divisors in T of the blow-ups
$D_3$
are (the strict transform of) the exceptional divisors in T of the blow-ups
 $\pi _R$
,
$\pi _R$
,
 $\pi _S$
and
$\pi _S$
and
 $\pi _T$
, respectively.
$\pi _T$
, respectively. -
•
 $D_{ij} := D_i \cap D_j$
and
$D_{ij} := D_i \cap D_j$
and
 $D_{123} := D_1 \cap D_2 \cap D_3$
are (smooth closed) strata of the exceptional locus of
$D_{123} := D_1 \cap D_2 \cap D_3$
are (smooth closed) strata of the exceptional locus of
 $\pi $
.
$\pi $
. -
•
 $I_{k} := \{ ([x_0: \ldots : x_k],[y_0:\ldots :y_k])\in \mathbb {P}^k \times \mathbb {P}^k | \sum ^k_{i=0} x_iy_i=0\}$
.
$I_{k} := \{ ([x_0: \ldots : x_k],[y_0:\ldots :y_k])\in \mathbb {P}^k \times \mathbb {P}^k | \sum ^k_{i=0} x_iy_i=0\}$
. -
•
 $\operatorname {Hom}^{\omega }_k(W, V)$
is the subspace of linear maps in
$\operatorname {Hom}^{\omega }_k(W, V)$
is the subspace of linear maps in
 $\operatorname {Hom}^{\omega }(W, V)$
of rank
$\operatorname {Hom}^{\omega }(W, V)$
of rank
 $\leq k$
.
$\leq k$
. -
•
 $\operatorname {Gr}^{\omega }(k,V)$
is the Grassmanian of k-dimensional linear subspaces of V, isotropic with respect to the symplectic form
$\operatorname {Gr}^{\omega }(k,V)$
is the Grassmanian of k-dimensional linear subspaces of V, isotropic with respect to the symplectic form
 $\omega $
.
$\omega $
. -
•
 $\hat {\mathbb {P}}^5$
is the blow-up of
$\hat {\mathbb {P}}^5$
is the blow-up of
 $\mathbb {P}^5 \simeq \mathbb {P}(S^2(W))$
(space of quadratic forms on W) along
$\mathbb {P}^5 \simeq \mathbb {P}(S^2(W))$
(space of quadratic forms on W) along
 $\mathbb {P}^2$
(locus of quadratic form of rank
$\mathbb {P}^2$
(locus of quadratic form of rank
 $1$
).
$1$
). -
•
 $\hat {Q}$
is the blow-up of
$\hat {Q}$
is the blow-up of
 $Q \subset \mathbb {P}(S^2(W))$
(space of degenerate quadratic forms on W) along
$Q \subset \mathbb {P}(S^2(W))$
(space of degenerate quadratic forms on W) along
 $\mathbb {P}^2$
(locus of quadratic form of rank
$\mathbb {P}^2$
(locus of quadratic form of rank
 $1$
).
$1$
).
Proposition 3.7 Geometry of the blow-ups
 $\pi _R$
,
$\pi _R$
,
 $\pi _S$
and
$\pi _S$
and
 $\pi _T$
$\pi _T$
-
1. The preimages
 $\pi ^{-1}_R(\Omega )$
,
$\pi ^{-1}_R(\Omega )$
,
 $(\pi _R \circ \pi _S)^{-1}(\Omega )$
and
$(\pi _R \circ \pi _S)^{-1}(\Omega )$
and
 $\pi ^{-1}(\Omega )$
are trivial fibrations over
$\pi ^{-1}(\Omega )$
are trivial fibrations over
 $\Omega $
;
$\Omega $
; -
2. The exceptional locus
 $\Omega _R$
of
$\Omega _R$
of
 $\pi _R$
is isomorphic to
$\pi _R$
is isomorphic to
 .
. -
3. Let
 $I^{\prime }_{2g-3}$
be the quotient of
$I^{\prime }_{2g-3}$
be the quotient of
 $I_{2g-3}$
by the involution which exchanges the coordinates
$I_{2g-3}$
by the involution which exchanges the coordinates
 $x_i$
and
$x_i$
and
 $y_i$
. A slice normal to
$y_i$
. A slice normal to
 in
in
 $\Omega _R$
is locally analytically isomorphic to an affine cone over
$\Omega _R$
is locally analytically isomorphic to an affine cone over
 $I^{\prime }_{2g-3}$
.
$I^{\prime }_{2g-3}$
. -
4. The singular locus
 $\Delta _S$
of S is the strict transform of
$\Delta _S$
of S is the strict transform of
 via
via
 $\pi _R$
, which is isomorphic to a
$\pi _R$
, which is isomorphic to a
 $\mathbb {P}^2$
-bundle over
$\mathbb {P}^2$
-bundle over
 $\operatorname {Gr}^{\omega }(2,V)\times \Omega $
.
$\operatorname {Gr}^{\omega }(2,V)\times \Omega $
. -
5. A slice normal to
 $\Delta _S$
in S is locally analytically isomorphic to the quotient
$\Delta _S$
in S is locally analytically isomorphic to the quotient
 $\mathbb {C}^{2g-3}/\pm 1$
.
$\mathbb {C}^{2g-3}/\pm 1$
.
Proof. Since
![]() $\Omega (C, \operatorname {SL}_2)$
is a collection of
$\Omega (C, \operatorname {SL}_2)$
is a collection of
![]() $2^{2g}$
points, (1) obviously holds. Consider now the étale cover
$2^{2g}$
points, (1) obviously holds. Consider now the étale cover
![]() $\tau \colon M(C, \operatorname {SL}_n) \times M(C, \operatorname {GL}_1) \to M(C, \operatorname {GL}_n)$
trivialising (4). For some (or any)
$\tau \colon M(C, \operatorname {SL}_n) \times M(C, \operatorname {GL}_1) \to M(C, \operatorname {GL}_n)$
trivialising (4). For some (or any)
![]() $x \in \Omega (C, \operatorname {SL}_n)$
we have
$x \in \Omega (C, \operatorname {SL}_n)$
we have
 $$ \begin{align*}\pi_{T(C, \operatorname{SL}_n)}^{-1}(x) \times \Omega(C, \operatorname{GL}_n) \simeq \pi_{T(C, \operatorname{SL}_n)}^{-1}(x) \times M(C, \operatorname{GL}_1) \simeq \pi_{T(C, \operatorname{GL}_n)}^{-1}(\Omega(C, \operatorname{GL}_n)),\end{align*} $$
$$ \begin{align*}\pi_{T(C, \operatorname{SL}_n)}^{-1}(x) \times \Omega(C, \operatorname{GL}_n) \simeq \pi_{T(C, \operatorname{SL}_n)}^{-1}(x) \times M(C, \operatorname{GL}_1) \simeq \pi_{T(C, \operatorname{GL}_n)}^{-1}(\Omega(C, \operatorname{GL}_n)),\end{align*} $$
since
![]() $\tau $
is étale. Thus, (1) holds for
$\tau $
is étale. Thus, (1) holds for
![]() $G=\operatorname {GL}_2$
, too.
$G=\operatorname {GL}_2$
, too.
(2), (3), (4), (5) follow instead from Proposition 3.4.(2), [Reference O’Grady56, (1.7.12) and (1.7.16)], [Reference O’Grady56, (3.5.1)] and [Reference O’Grady56, (3.5.1)] respectively; alternatively, see the proof of [Reference Choy and Kiem8, Proposition 3.2].
Proposition 3.8 The exceptional divisors of
 $\pi _T$
$\pi _T$
-
1.
 $D_1$
is a
$D_1$
is a
 $\hat {\mathbb {P}}^5$
-bundle over
$\hat {\mathbb {P}}^5$
-bundle over
 $\operatorname {Gr}^{\omega }(3,V) \times \Omega $
.
$\operatorname {Gr}^{\omega }(3,V) \times \Omega $
. -
2. There exists a vector bundle
 $\mathcal {E}$
on
$\mathcal {E}$
on
 $\Sigma ^{\circ }_{\iota }$
such that
$\Sigma ^{\circ }_{\iota }$
such that
 $D^{\circ }_2$
is the quotient of the
$D^{\circ }_2$
is the quotient of the
 $I_{2g-3}$
-bundle
$I_{2g-3}$
-bundle
 $\mathbb {I}_{2g-3}$
in
$\mathbb {I}_{2g-3}$
in
 $\mathbb {P}(\mathcal {E}) \times \mathbb {P}(\mathcal {E}^*)$
by the involution
$\mathbb {P}(\mathcal {E}) \times \mathbb {P}(\mathcal {E}^*)$
by the involution
 $\iota '$
extending the involution
$\iota '$
extending the involution $$ \begin{align*} \iota'\colon \mathbb{P}(\mathcal{E}) \times \mathbb{P}(\mathcal{E}^*) & \to \mathbb{P}(\mathcal{E}) \times \mathbb{P}(\mathcal{E}^*),\\ (v, [x_i], [y_j]) & \mapsto (\iota(v), [y_j], [x_i]), \end{align*} $$
$$ \begin{align*} \iota'\colon \mathbb{P}(\mathcal{E}) \times \mathbb{P}(\mathcal{E}^*) & \to \mathbb{P}(\mathcal{E}) \times \mathbb{P}(\mathcal{E}^*),\\ (v, [x_i], [y_j]) & \mapsto (\iota(v), [y_j], [x_i]), \end{align*} $$
 $\iota $
on
$\iota $
on
 $\Sigma ^{\circ }_{\iota }$
defined in Definition 3.3.
$\Sigma ^{\circ }_{\iota }$
defined in Definition 3.3.
-
3.
 $D_3$
is a
$D_3$
is a
 $\mathbb {P}^{2g-4}$
-bundle over a (Zariski locally trivial)
$\mathbb {P}^{2g-4}$
-bundle over a (Zariski locally trivial)
 $\mathbb {P}^2$
-bundle over
$\mathbb {P}^2$
-bundle over
 $\operatorname {Gr}^{\omega }(2,V) \times \Omega $
.
$\operatorname {Gr}^{\omega }(2,V) \times \Omega $
. -
4.
 $D_{13}$
is a
$D_{13}$
is a
 $\hat {Q}$
-bundle over
$\hat {Q}$
-bundle over
 $\operatorname {Gr}^{\omega }(3,V) \times \Omega $
.
$\operatorname {Gr}^{\omega }(3,V) \times \Omega $
.
Proof. Let
![]() $\mathcal {U}_m$
be the universal bundle over
$\mathcal {U}_m$
be the universal bundle over
![]() $\operatorname {Gr}^{\omega }(m, V)$
, with
$\operatorname {Gr}^{\omega }(m, V)$
, with
![]() $m=2,3$
, and
$m=2,3$
, and
![]() $\operatorname {Hom}_k(W, \mathcal {U}_m)$
be the subbundle of
$\operatorname {Hom}_k(W, \mathcal {U}_m)$
be the subbundle of
![]() $\operatorname {Hom}(W, \mathcal {U}_m)$
of rank
$\operatorname {Hom}(W, \mathcal {U}_m)$
of rank
![]() $\leq k$
. The quotient space
$\leq k$
. The quotient space
is isomorphic to the space of quadrics
![]() $\mathbb {P}(S^2_k \mathcal {U}_m)$
of rank
$\mathbb {P}(S^2_k \mathcal {U}_m)$
of rank
![]() $\leq k$
. There are obvious forgetful maps
$\leq k$
. There are obvious forgetful maps
 $$ \begin{align*} f_3\colon & \mathbb{P}\operatorname{Hom}(W, \mathcal{U}_3) \to \mathbb{P}\operatorname{Hom}^{\omega}(W,V)\\ f_2 \colon & \mathbb{P}\operatorname{Hom}_2(W, \mathcal{U}_2) \to \mathbb{P}\operatorname{Hom}^{\omega}_2(W,V), \end{align*} $$
$$ \begin{align*} f_3\colon & \mathbb{P}\operatorname{Hom}(W, \mathcal{U}_3) \to \mathbb{P}\operatorname{Hom}^{\omega}(W,V)\\ f_2 \colon & \mathbb{P}\operatorname{Hom}_2(W, \mathcal{U}_2) \to \mathbb{P}\operatorname{Hom}^{\omega}_2(W,V), \end{align*} $$
which induces the following diagrams


A proof of the isomorphisms above is provided in [Reference O’Grady56, (3.1.1) and (3.5.1)]; alternatively, see [Reference Choy and Kiem8, Proposition 3.2]. This shows (1), (3), (4). To show (2), one can repeat the argument of [Reference Choy and Kiem8, Proposition 3.2.(2)] verbatim.
Proposition 3.9.
![]() $\operatorname {Gr}^{\omega }(m,V)$
and the fibres of
$\operatorname {Gr}^{\omega }(m,V)$
and the fibres of
![]() $\Delta _S$
,
$\Delta _S$
,
![]() $D_1$
,
$D_1$
,
![]() $D_3$
,
$D_3$
,
![]() $D_{13}$
and
$D_{13}$
and
![]() $\Omega _S$
over
$\Omega _S$
over
![]() $\Omega $
have pure cohomology of Hodge–Tate type. In particular, they do not have odd cohomology. Their E-polynomials are
$\Omega $
have pure cohomology of Hodge–Tate type. In particular, they do not have odd cohomology. Their E-polynomials are
 $$ \begin{align*} E(\operatorname{Gr}^{\omega}(2,V)) & = \frac{(1-q^{2g-2})(1-q^{2g})}{(1-q)(1-q^2)}\\ E(\operatorname{Gr}^{\omega}(3,V)) & = \frac{(1-q^{2g-4})(1-q^{2g-2})(1-q^{2g})}{(1-q)(1-q^2)(1-q^3)}\\ E(\Delta_S) & = \frac{(1-q^3)(1-q^{2g-2})(1-q^{2g})}{(1-q)^2(1-q^2)} \cdot E(\Omega)\\ E(D_1) & = \frac{(1-q^4)(1-q^{2g-4})(1-q^{2g-2})(1-q^{2g})}{(1-q)^3(1-q^2)} \cdot E(\Omega)\\ E(D_3) & = \frac{(1-q^{3})(1-q^{2g-3})(1-q^{2g-2})(1-q^{2g})}{(1-q)^3 (1-q^2)} \cdot E(\Omega)\\ E(D_{13}) & = \frac{(1-q^{3})(1-q^{2g-4})(1-q^{2g-2})(1-q^{2g})}{(1-q)^3 (1-q^2)} \cdot E(\Omega)\\ E(\Omega_S) & = E(D_1)-E(\Delta_S) \cdot \sum^{2g-6}_{i=0} q^{i+1} \\ & = \frac{(1-q^{2g-2})(1-q^{2g-1})(1-q^{2g})}{(1-q)^2(1-q^2)} \cdot E(\Omega). \end{align*} $$
$$ \begin{align*} E(\operatorname{Gr}^{\omega}(2,V)) & = \frac{(1-q^{2g-2})(1-q^{2g})}{(1-q)(1-q^2)}\\ E(\operatorname{Gr}^{\omega}(3,V)) & = \frac{(1-q^{2g-4})(1-q^{2g-2})(1-q^{2g})}{(1-q)(1-q^2)(1-q^3)}\\ E(\Delta_S) & = \frac{(1-q^3)(1-q^{2g-2})(1-q^{2g})}{(1-q)^2(1-q^2)} \cdot E(\Omega)\\ E(D_1) & = \frac{(1-q^4)(1-q^{2g-4})(1-q^{2g-2})(1-q^{2g})}{(1-q)^3(1-q^2)} \cdot E(\Omega)\\ E(D_3) & = \frac{(1-q^{3})(1-q^{2g-3})(1-q^{2g-2})(1-q^{2g})}{(1-q)^3 (1-q^2)} \cdot E(\Omega)\\ E(D_{13}) & = \frac{(1-q^{3})(1-q^{2g-4})(1-q^{2g-2})(1-q^{2g})}{(1-q)^3 (1-q^2)} \cdot E(\Omega)\\ E(\Omega_S) & = E(D_1)-E(\Delta_S) \cdot \sum^{2g-6}_{i=0} q^{i+1} \\ & = \frac{(1-q^{2g-2})(1-q^{2g-1})(1-q^{2g})}{(1-q)^2(1-q^2)} \cdot E(\Omega). \end{align*} $$
Proof. Note that
![]() $\operatorname {Gr}^{\omega }(m,V)$
is a smooth projective variety whose cohomology is of Hodge–Tate type; see, for instance, [Reference Choy and Kiem8, Lemma 3.1]. Hence, the fibres of
$\operatorname {Gr}^{\omega }(m,V)$
is a smooth projective variety whose cohomology is of Hodge–Tate type; see, for instance, [Reference Choy and Kiem8, Lemma 3.1]. Hence, the fibres of
![]() $\Delta _S$
,
$\Delta _S$
,
![]() $D_1$
,
$D_1$
,
![]() $D_3$
and
$D_3$
and
![]() $D_1 \cap D_3$
over
$D_1 \cap D_3$
over
![]() $\Omega $
have pure cohomology of Hodge–Tate type by Proposition 3.7 and 3.8. Since
$\Omega $
have pure cohomology of Hodge–Tate type by Proposition 3.7 and 3.8. Since
![]() $\Omega _S$
has only quotient singularities, the natural inclusion
$\Omega _S$
has only quotient singularities, the natural inclusion
![]() $H^*(\Omega _S) \simeq IH^*(\Omega _S) \hookrightarrow H^*(D_1)$
implies that the fibres of
$H^*(\Omega _S) \simeq IH^*(\Omega _S) \hookrightarrow H^*(D_1)$
implies that the fibres of
![]() $\Omega _S$
over
$\Omega _S$
over
![]() $\Omega $
have pure cohomology of Hodge–Tate type. The computation of the E-polynomials follows immediately from [Reference Choy and Kiem8, Lemma 3.1], Proposition 3.7 and 3.8, except maybe for
$\Omega $
have pure cohomology of Hodge–Tate type. The computation of the E-polynomials follows immediately from [Reference Choy and Kiem8, Lemma 3.1], Proposition 3.7 and 3.8, except maybe for
![]() $\Omega _S$
. In that case, we use the decomposition theorem for the blow-up map
$\Omega _S$
. In that case, we use the decomposition theorem for the blow-up map
![]() $\pi _T|_{D_1}$
, which actually reduces to [Reference Voisin67, Theorem 7.31].
$\pi _T|_{D_1}$
, which actually reduces to [Reference Voisin67, Theorem 7.31].
3.3 The incidence variety
 $I_{2g-3}$
$I_{2g-3}$
The incidence variety
![]() $I_{2g-3} \subset \mathbb {P}^{2g-3} \times \mathbb {P}^{2g-3}$
is the projectivisation of the vector bundle
$I_{2g-3} \subset \mathbb {P}^{2g-3} \times \mathbb {P}^{2g-3}$
is the projectivisation of the vector bundle
![]() $\Omega ^1_{\mathbb {P}^{2g-3}}(1)$
over
$\Omega ^1_{\mathbb {P}^{2g-3}}(1)$
over
![]() $\mathbb {P}^{2g-3}$
. Hence, we can write
$\mathbb {P}^{2g-3}$
. Hence, we can write
 $$ \begin{align} H^*(I_{2g-3}) = \mathbb{Q}[a,b]/(a^{2g-2}, b^{2g-2}, \sum^{2g-3}_{i=0} (-1)^i a^{2g-3-i} b^{i}), \end{align} $$
$$ \begin{align} H^*(I_{2g-3}) = \mathbb{Q}[a,b]/(a^{2g-2}, b^{2g-2}, \sum^{2g-3}_{i=0} (-1)^i a^{2g-3-i} b^{i}), \end{align} $$
where a and b have degree
![]() $2$
, and they are pullback of the first Chern classes of the tautological line bundle of
$2$
, and they are pullback of the first Chern classes of the tautological line bundle of
![]() $\mathbb {P}^{2g-3}$
via the two projections
$\mathbb {P}^{2g-3}$
via the two projections
![]() $I_{2g-3} \subset \mathbb {P}^{2g-3} \times \mathbb {P}^{2g-3} \to \mathbb {P}^{2g-3}$
. Note that
$I_{2g-3} \subset \mathbb {P}^{2g-3} \times \mathbb {P}^{2g-3} \to \mathbb {P}^{2g-3}$
. Note that
![]() $I_{2g-3}$
has no odd cohomology.
$I_{2g-3}$
has no odd cohomology.
The involution which exchanges the factors of the product
![]() $\mathbb {P}^{2g-3} \times \mathbb {P}^{2g-3}$
leaves
$\mathbb {P}^{2g-3} \times \mathbb {P}^{2g-3}$
leaves
![]() $I_{2g-3}$
invariant and in cohomology exchanges the classes a and b. Consider the decomposition into eigenspaces for the involution (relative to eigenvalues
$I_{2g-3}$
invariant and in cohomology exchanges the classes a and b. Consider the decomposition into eigenspaces for the involution (relative to eigenvalues
![]() $\pm 1$
respectively)
$\pm 1$
respectively)
For
![]() $d=2k<4g-7$
, we have
$d=2k<4g-7$
, we have
 $$ \begin{align*} H^d(I_{2g-3})^+ = H^d(\mathbb{P}^{2g-3}\times \mathbb{P}^{2g-3})^+ = \langle a^ib^j | i+j=d\rangle^+ = \langle a^ib^j + a^j b^i| i+j=d\rangle. \end{align*} $$
$$ \begin{align*} H^d(I_{2g-3})^+ = H^d(\mathbb{P}^{2g-3}\times \mathbb{P}^{2g-3})^+ = \langle a^ib^j | i+j=d\rangle^+ = \langle a^ib^j + a^j b^i| i+j=d\rangle. \end{align*} $$
Therefore, we obtain that
 $$ \begin{align*} \dim H^{2k}(I_{2g-3})=k+1, \,\, \dim H^{2k}(I_{2g-3})^+=\left\lceil \frac{k+1}{2} \right\rceil, \,\, \dim H^{2k}(I_{2g-3})^-=\left\lceil \frac{k}{2} \right\rceil. \end{align*} $$
$$ \begin{align*} \dim H^{2k}(I_{2g-3})=k+1, \,\, \dim H^{2k}(I_{2g-3})^+=\left\lceil \frac{k+1}{2} \right\rceil, \,\, \dim H^{2k}(I_{2g-3})^-=\left\lceil \frac{k}{2} \right\rceil. \end{align*} $$
Proposition 3.10. Setting
![]() $q := t^2=uv$
, the Poincaré polynomials (equivalently E-polynomials) of
$q := t^2=uv$
, the Poincaré polynomials (equivalently E-polynomials) of
![]() $I_{2g-3}$
of the invariant and variant parts of its cohomology are
$I_{2g-3}$
of the invariant and variant parts of its cohomology are
 $$ \begin{align} P_t(I_{2g-3}) & = E(I_{2g-3}) = \frac{(1-q^{2g-2})(1-q^{2g-3})}{(1-q)^2} \end{align} $$
$$ \begin{align} P_t(I_{2g-3}) & = E(I_{2g-3}) = \frac{(1-q^{2g-2})(1-q^{2g-3})}{(1-q)^2} \end{align} $$
 $$ \begin{align} P_t(I_{2g-3})^+ & = E(I_{2g-3})^+ = \frac{(1-q^{2g-2})^2}{(1-q^2)(1-q)} \end{align} $$
$$ \begin{align} P_t(I_{2g-3})^+ & = E(I_{2g-3})^+ = \frac{(1-q^{2g-2})^2}{(1-q^2)(1-q)} \end{align} $$
 $$ \begin{align} P_t(I_{2g-3})^- & = E(I_{2g-3})^- = q \frac{(1-q^{2g-2})(1-q^{2g-4})}{(1-q^2)(1-q)}. \end{align} $$
$$ \begin{align} P_t(I_{2g-3})^- & = E(I_{2g-3})^- = q \frac{(1-q^{2g-2})(1-q^{2g-4})}{(1-q^2)(1-q)}. \end{align} $$
Proof.
![]() $I_{2g-3}$
is a
$I_{2g-3}$
is a
![]() $\mathbb {P}^{2g-4}$
-bundle over
$\mathbb {P}^{2g-4}$
-bundle over
![]() $\mathbb {P}^{2g-3}$
, and this gives (14). We now estimate
$\mathbb {P}^{2g-3}$
, and this gives (14). We now estimate
![]() $P_t(I_{2g-3})^+ - P_t(I_{2g-3})^-$
. For
$P_t(I_{2g-3})^+ - P_t(I_{2g-3})^-$
. For
![]() $d=2k<4g-7$
, we have
$d=2k<4g-7$
, we have
 $$ \begin{align*}\dim H^{2k}(I_{2g-3})^+ - \dim H^{2k}(I_{2g-3})^- = \left\lceil \frac{k+1}{2} \right\rceil- \left\lceil \frac{k}{2} \right\rceil = \begin{cases} 1 & \text{ for } k=2l,\\ 0 & \text{ for } k=2l+1. \end{cases}\end{align*} $$
$$ \begin{align*}\dim H^{2k}(I_{2g-3})^+ - \dim H^{2k}(I_{2g-3})^- = \left\lceil \frac{k+1}{2} \right\rceil- \left\lceil \frac{k}{2} \right\rceil = \begin{cases} 1 & \text{ for } k=2l,\\ 0 & \text{ for } k=2l+1. \end{cases}\end{align*} $$
Since the polarisation
![]() $\mathcal {O}(1,1)$
is
$\mathcal {O}(1,1)$
is
![]() $\iota $
-invariant, the hard Lefschetz theorem gives
$\iota $
-invariant, the hard Lefschetz theorem gives
![]() $\dim H^{d}(I_{2g-3})^{\pm } = \dim H^{8g-14 - d}(I_{2g-3})^{\pm }$
. Thus, we can write
$\dim H^{d}(I_{2g-3})^{\pm } = \dim H^{8g-14 - d}(I_{2g-3})^{\pm }$
. Thus, we can write
 $$ \begin{align} P_t(I_{2g-3})^+ - P_t(I_{2g-3})^- = \sum^{g-2}_{l=0}q^{2l} + q^{2g-3} \sum^{g-2}_{l=0}q^{2l} = \frac{(1-q^{2g-2})(1+q^{2g-3})}{(1-q^2)}. \end{align} $$
$$ \begin{align} P_t(I_{2g-3})^+ - P_t(I_{2g-3})^- = \sum^{g-2}_{l=0}q^{2l} + q^{2g-3} \sum^{g-2}_{l=0}q^{2l} = \frac{(1-q^{2g-2})(1+q^{2g-3})}{(1-q^2)}. \end{align} $$
Finally, substituting (14) and (17) in
 $$ \begin{align*} P_t(I_{2g-3})^+ & = \frac{1}{2}(P_t(I_{2g-3}) + ( P_t(I_{2g-3})^+ - P_t(I_{2g-3})^- ))\\ P_t(I_{2g-3})^- & = P_t(I_{2g-3}) - P_t(I_{2g-3})^+, \end{align*} $$
$$ \begin{align*} P_t(I_{2g-3})^+ & = \frac{1}{2}(P_t(I_{2g-3}) + ( P_t(I_{2g-3})^+ - P_t(I_{2g-3})^- ))\\ P_t(I_{2g-3})^- & = P_t(I_{2g-3}) - P_t(I_{2g-3})^+, \end{align*} $$
3.4 Intersection cohomology of local models
The goal of this section is to compute the intersection cohomology of the normal slices
![]() $N_{\Sigma }$
and
$N_{\Sigma }$
and
![]() $N_{\Omega }$
. This is an important step to determine the summands of the decomposition theorem in Theorem 1.2.
$N_{\Omega }$
. This is an important step to determine the summands of the decomposition theorem in Theorem 1.2.
Proposition 3.11. Let
![]() $N_{\Sigma }$
be a slice normal to
$N_{\Sigma }$
be a slice normal to
![]() $\Sigma $
at a point in
$\Sigma $
at a point in
![]() $\Sigma \setminus \Omega $
. Then
$\Sigma \setminus \Omega $
. Then
 $$ \begin{align} IH^d(N_{\Sigma}) \simeq \begin{cases} H^{d}_{\mathrm{prim}}(I_{2g-3}) \simeq \mathbb{Q} & \text{ for } d=2k<4g-6,\\ 0 & \text{ otherwise.}\\ \end{cases} \end{align} $$
$$ \begin{align} IH^d(N_{\Sigma}) \simeq \begin{cases} H^{d}_{\mathrm{prim}}(I_{2g-3}) \simeq \mathbb{Q} & \text{ for } d=2k<4g-6,\\ 0 & \text{ otherwise.}\\ \end{cases} \end{align} $$
 $$ \begin{align} IH^{2k}(N_{\Sigma}) \subseteq \begin{cases} H^{2k}(I_{2g-3})^+ & \text{ for } k=2l,\\ H^{2k}(I_{2g-3})^- & \text{ for } k=2l+1. \end{cases} \end{align} $$
$$ \begin{align} IH^{2k}(N_{\Sigma}) \subseteq \begin{cases} H^{2k}(I_{2g-3})^+ & \text{ for } k=2l,\\ H^{2k}(I_{2g-3})^- & \text{ for } k=2l+1. \end{cases} \end{align} $$
Proof. (18) follows from Proposition 2.1, since
![]() $N_{\Sigma }$
is locally isomorphic to an affine cone over the smooth variety
$N_{\Sigma }$
is locally isomorphic to an affine cone over the smooth variety
![]() $I_{2g-3}$
(with
$I_{2g-3}$
(with
![]() $\iota $
-invariant conormal bundle
$\iota $
-invariant conormal bundle
![]() $\mathcal {O}(1,1)$
) by Proposition 3.4.(1).
$\mathcal {O}(1,1)$
) by Proposition 3.4.(1).
Since
![]() $\mathcal {O}(1,1)$
is
$\mathcal {O}(1,1)$
is
![]() $\iota $
-invariant,
$\iota $
-invariant,
 $H^d_{\mathrm {prim}}(I_{2g-3})$
is
$H^d_{\mathrm {prim}}(I_{2g-3})$
is
![]() $\iota $
-invariant, too. Hence, (19) follows from the following dimensional argument:
$\iota $
-invariant, too. Hence, (19) follows from the following dimensional argument:
 $$ \begin{align*} 1 \geq \dim IH^{2k}(N_\Sigma) \geq \dim IH^{2k}(N_\Sigma)^+ & = \dim H^{2k}(I_{2g-3})^+ - \dim H^{2k-2}(I_{2g-3})^+ \nonumber \\ & = \left\lceil \frac{k+1}{2} \right\rceil- \left\lceil \frac{k}{2} \right\rceil = \begin{cases} 1 & \text{ for } k=2l,\\ 0 & \text{ for } k=2l+1. \end{cases} \\[-38pt] \end{align*} $$
$$ \begin{align*} 1 \geq \dim IH^{2k}(N_\Sigma) \geq \dim IH^{2k}(N_\Sigma)^+ & = \dim H^{2k}(I_{2g-3})^+ - \dim H^{2k-2}(I_{2g-3})^+ \nonumber \\ & = \left\lceil \frac{k+1}{2} \right\rceil- \left\lceil \frac{k}{2} \right\rceil = \begin{cases} 1 & \text{ for } k=2l,\\ 0 & \text{ for } k=2l+1. \end{cases} \\[-38pt] \end{align*} $$
Proposition 3.12. Let
![]() $N_{\Sigma _R \cap \Omega _R}$
be a slice normal to
$N_{\Sigma _R \cap \Omega _R}$
be a slice normal to
![]() $\Sigma _R \cap \Omega _R$
in
$\Sigma _R \cap \Omega _R$
in
![]() $\Omega _R$
. Then
$\Omega _R$
. Then
 $$ \begin{align} IH^d(N_{\Sigma_R \cap \Omega_R}) \simeq \begin{cases} H^d_{\mathrm{prim}}(I^{\prime}_{2g-3}) \simeq \mathbb{Q} & \text{ for } d=4k<4g-6,\\ 0 & \text{ otherwise}. \end{cases} \end{align} $$
$$ \begin{align} IH^d(N_{\Sigma_R \cap \Omega_R}) \simeq \begin{cases} H^d_{\mathrm{prim}}(I^{\prime}_{2g-3}) \simeq \mathbb{Q} & \text{ for } d=4k<4g-6,\\ 0 & \text{ otherwise}. \end{cases} \end{align} $$
In particular,
 $$ \begin{align} \dim H^{4g-6+2i}(I^{\prime}_{2g-3}) - \dim IH^{4g-6+2i}(N_{\Sigma_R \cap \Omega_R}) = \left\lceil \frac{2g-3-|i|}{2}\right\rceil. \end{align} $$
$$ \begin{align} \dim H^{4g-6+2i}(I^{\prime}_{2g-3}) - \dim IH^{4g-6+2i}(N_{\Sigma_R \cap \Omega_R}) = \left\lceil \frac{2g-3-|i|}{2}\right\rceil. \end{align} $$
Proof.
Proposition 2.1 and 3.7.(3) give (20), while (21) follows immediately from
 $ H^{2k}(I^{\prime }_{2g-3}) = H^{2k}(I_{2g-3})^+ $
.
$ H^{2k}(I^{\prime }_{2g-3}) = H^{2k}(I_{2g-3})^+ $
.
Proposition 3.13. The intersection E-polynomial of
![]() $\Omega _R$
is
$\Omega _R$
is
 $$ \begin{align*}IE(\Omega_R) = \frac{(1-q^{4g-4})(1-q^{2g})}{(1-q)(1-q^2)}\cdot E(\Omega).\end{align*} $$
$$ \begin{align*}IE(\Omega_R) = \frac{(1-q^{4g-4})(1-q^{2g})}{(1-q)(1-q^2)}\cdot E(\Omega).\end{align*} $$
Proof. We apply the decomposition theorem to the restriction of
![]() $\pi _S$
to the strict transform
$\pi _S$
to the strict transform
 $\Omega _S := \pi ^{-1}_{S, *} \Omega _R$
.
$\Omega _S := \pi ^{-1}_{S, *} \Omega _R$
.
By Proposition 3.7.(3), the defect of semismallness of
![]() $\pi _S|_{\Omega _S}$
is
$\pi _S|_{\Omega _S}$
is
 $$ \begin{align*} r(\pi_S|_{\Omega_S}) & := \dim \Omega_S \times_{\Omega_R} \Omega_S - \dim \Omega_R \\ & = 2 \dim I^{\prime}_{2g-3} + \dim \Sigma_ R \cap \Omega_R - \dim \Omega_R = 4g-8, \end{align*} $$
$$ \begin{align*} r(\pi_S|_{\Omega_S}) & := \dim \Omega_S \times_{\Omega_R} \Omega_S - \dim \Omega_R \\ & = 2 \dim I^{\prime}_{2g-3} + \dim \Sigma_ R \cap \Omega_R - \dim \Omega_R = 4g-8, \end{align*} $$
and
![]() $\Sigma _ R \cap \Omega _R$
is the only support of the decomposition theorem for
$\Sigma _ R \cap \Omega _R$
is the only support of the decomposition theorem for
![]() $\pi _S|_{\Omega _S}$
. Note that
$\pi _S|_{\Omega _S}$
. Note that
 $R^i \pi _{S, *} \mathbb {Q}_{\pi ^{-1}_S(\Sigma _ R \cap \Omega _R)}$
are trivial local systems over
$R^i \pi _{S, *} \mathbb {Q}_{\pi ^{-1}_S(\Sigma _ R \cap \Omega _R)}$
are trivial local systems over
![]() $\Sigma _ R \cap \Omega _R \simeq \mathbb {P}^{2g-1} \times \Omega $
, because of Proposition 3.7.(1) and the simple connectedness of
$\Sigma _ R \cap \Omega _R \simeq \mathbb {P}^{2g-1} \times \Omega $
, because of Proposition 3.7.(1) and the simple connectedness of
![]() $\mathbb {P}^{2g-1}$
. Hence, there exist integers
$\mathbb {P}^{2g-1}$
. Hence, there exist integers
![]() $a(i)$
such that
$a(i)$
such that
 $$ \begin{align*} R(\pi_{S}|_{\Omega_S})_{*} {\mathbb{Q}} [\dim {\Omega}_S] & = \bigoplus^{4g-8}_{i=-4g+8} {{}^{\mathfrak{p}}}{\mathcal{H}}^i((\pi_{S}|_{\Omega_S})_{*} {\mathbb{Q}}[\dim \Omega_S])[-i]\\ & = IC_{\Omega_R} \oplus {\bigoplus}^{2g-4}_{i=-2g+4} {\mathbb{Q}}^{a(i)}_{\Sigma_{R} \cap {\Omega}_R}[\dim{\Sigma}_ R \cap {\Omega}_R-2i](-2g+3-i). \end{align*} $$
$$ \begin{align*} R(\pi_{S}|_{\Omega_S})_{*} {\mathbb{Q}} [\dim {\Omega}_S] & = \bigoplus^{4g-8}_{i=-4g+8} {{}^{\mathfrak{p}}}{\mathcal{H}}^i((\pi_{S}|_{\Omega_S})_{*} {\mathbb{Q}}[\dim \Omega_S])[-i]\\ & = IC_{\Omega_R} \oplus {\bigoplus}^{2g-4}_{i=-2g+4} {\mathbb{Q}}^{a(i)}_{\Sigma_{R} \cap {\Omega}_R}[\dim{\Sigma}_ R \cap {\Omega}_R-2i](-2g+3-i). \end{align*} $$
At the stalk level, at
![]() $x \in \Sigma _R \cap \Omega _R$
, we obtain by (21)
$x \in \Sigma _R \cap \Omega _R$
, we obtain by (21)
 $$ \begin{align*} a(i) = \dim H^{4g-6+2i}(I^{\prime}_{2g-3})-\dim IH^{4g-6+2i}(N_{\Sigma_{R} \cap \Omega_R}) = \left\lceil \frac{2g-3-|i|}{2}\right\rceil. \end{align*} $$
$$ \begin{align*} a(i) = \dim H^{4g-6+2i}(I^{\prime}_{2g-3})-\dim IH^{4g-6+2i}(N_{\Sigma_{R} \cap \Omega_R}) = \left\lceil \frac{2g-3-|i|}{2}\right\rceil. \end{align*} $$
Together with Proposition 3.9, we get
 $$ \begin{align*} IE(\Omega_R) &= E(\Omega_S) - E(\Omega) \cdot E(\mathbb{P}^{2g-1}) \cdot \sum^{2g-4}_{i=-2g+4}q^{2g-3+i} \left\lceil \frac{2g-3-|i|}{2}\right\rceil\\ & = \left( \frac{(1-q^{2g-2})(1-q^{2g-1})(1-q^{2g})}{(1-q)^2(1-q^2)} - \frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})(1-q^{2g})}{(1-q)^2 (1-q^2)} \right) \cdot E(\Omega)\\ & = \frac{(1-q^{4g-4})(1-q^{2g})}{(1-q)(1-q^2)} \cdot E(\Omega).\\[-40pt] \end{align*} $$
$$ \begin{align*} IE(\Omega_R) &= E(\Omega_S) - E(\Omega) \cdot E(\mathbb{P}^{2g-1}) \cdot \sum^{2g-4}_{i=-2g+4}q^{2g-3+i} \left\lceil \frac{2g-3-|i|}{2}\right\rceil\\ & = \left( \frac{(1-q^{2g-2})(1-q^{2g-1})(1-q^{2g})}{(1-q)^2(1-q^2)} - \frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})(1-q^{2g})}{(1-q)^2 (1-q^2)} \right) \cdot E(\Omega)\\ & = \frac{(1-q^{4g-4})(1-q^{2g})}{(1-q)(1-q^2)} \cdot E(\Omega).\\[-40pt] \end{align*} $$
Proposition 3.14. Let
![]() $N_{\Omega }$
be a slice normal to
$N_{\Omega }$
be a slice normal to
![]() $\Omega $
. Then
$\Omega $
. Then
![]() $IH^*(N_{\Omega })$
is pure of Hodge–Tate type with intersection Poincaré polynomial (equivalently, intersection E-polynomials)
$IH^*(N_{\Omega })$
is pure of Hodge–Tate type with intersection Poincaré polynomial (equivalently, intersection E-polynomials)
 $$ \begin{align*}IP_t(N_{\Omega}) = IE(N_{\Omega}) = \frac{1-q^{2g}}{1-q^2}.\end{align*} $$
$$ \begin{align*}IP_t(N_{\Omega}) = IE(N_{\Omega}) = \frac{1-q^{2g}}{1-q^2}.\end{align*} $$
Proof. Since
 $IH^*(N_{\Omega }) \hookrightarrow IH^*(\pi _R ^{-1}(x))$
for some
$IH^*(N_{\Omega }) \hookrightarrow IH^*(\pi _R ^{-1}(x))$
for some
![]() $x \in \Omega $
,
$x \in \Omega $
,
![]() $IH^*(N_{\Omega })$
is pure of Hodge–Tate type by Proposition 3.9.
$IH^*(N_{\Omega })$
is pure of Hodge–Tate type by Proposition 3.9.
Recall now that
![]() $N_{\Omega }$
is an affine cone over
$N_{\Omega }$
is an affine cone over
![]() $\Omega _R$
by Proposition 3.2.(2). Hence, Proposition 2.1 implies that the intersection Poincaré polynomial
$\Omega _R$
by Proposition 3.2.(2). Hence, Proposition 2.1 implies that the intersection Poincaré polynomial
![]() $IP_t(N_{\Omega })$
is a polynomial in the variable
$IP_t(N_{\Omega })$
is a polynomial in the variable
![]() $q = t^2$
of degree at most
$q = t^2$
of degree at most
![]() $3g-4$
, given by
$3g-4$
, given by
 $$ \begin{align*} IE(N_{\Omega})&=[IE(\pi_R ^{-1}(x))-q IE(\pi_R ^{-1}(x))]_{\leq 3g-4}= \frac{1}{E(\Omega)}[IE(\Omega_R)-q IE(\Omega_R)]_{\leq 3g-4} \\ & = \bigg[ \frac{(1-q^{4g-4})(1-q^{2g})}{(1-q^2)}\bigg]_{\leq 3g-4} = \frac{1-q^{2g}}{1-q^2}.\\[-40pt] \end{align*} $$
$$ \begin{align*} IE(N_{\Omega})&=[IE(\pi_R ^{-1}(x))-q IE(\pi_R ^{-1}(x))]_{\leq 3g-4}= \frac{1}{E(\Omega)}[IE(\Omega_R)-q IE(\Omega_R)]_{\leq 3g-4} \\ & = \bigg[ \frac{(1-q^{4g-4})(1-q^{2g})}{(1-q^2)}\bigg]_{\leq 3g-4} = \frac{1-q^{2g}}{1-q^2}.\\[-40pt] \end{align*} $$
4 Decomposition theorem
Proof of Theorem 1.2. Let
![]() $\pi ^{\circ }_T$
be the restriction of
$\pi ^{\circ }_T$
be the restriction of
![]() $\pi _T$
over
$\pi _T$
over
![]() $M^{\circ } := M \setminus \Omega $
. By Proposition 3.2.(1) the defect of semismallness of
$M^{\circ } := M \setminus \Omega $
. By Proposition 3.2.(1) the defect of semismallness of
![]() $\pi ^{\circ }_T$
is
$\pi ^{\circ }_T$
is
 $$ \begin{align*} r(\pi^{\circ}_T) & := \dim \pi^{-1}_T(M^{\circ}) \times_{M^{\circ}} \pi^{-1}_T(M^{\circ}) - \dim M \\ & = 2 \dim I_{2g-3} + \dim \Sigma - \dim M = 4g-8, \end{align*} $$
$$ \begin{align*} r(\pi^{\circ}_T) & := \dim \pi^{-1}_T(M^{\circ}) \times_{M^{\circ}} \pi^{-1}_T(M^{\circ}) - \dim M \\ & = 2 \dim I_{2g-3} + \dim \Sigma - \dim M = 4g-8, \end{align*} $$
and
![]() $\Sigma ^\circ $
is the only support of the decomposition theorem for
$\Sigma ^\circ $
is the only support of the decomposition theorem for
![]() $\pi ^{\circ }_T$
. Hence, there exists a splitting
$\pi ^{\circ }_T$
. Hence, there exists a splitting
 $$ \begin{align*} R \pi^{\circ}_{T, *} \mathbb{Q}[\dim T]= IC_{M^\circ} \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathscr{L}_i[\dim \Sigma -2i] \end{align*} $$
$$ \begin{align*} R \pi^{\circ}_{T, *} \mathbb{Q}[\dim T]= IC_{M^\circ} \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathscr{L}_i[\dim \Sigma -2i] \end{align*} $$
for some semisimple local systems
![]() $\mathscr {L}_i$
supported on
$\mathscr {L}_i$
supported on
![]() $\Sigma ^\circ $
. Restricting to
$\Sigma ^\circ $
. Restricting to
 $D^\circ _2 = \pi ^{-1}_T(\Sigma ^{\circ })$
, we obtain
$D^\circ _2 = \pi ^{-1}_T(\Sigma ^{\circ })$
, we obtain
 $$ \begin{align*} R (\pi^{\circ}_{T|_{D^\circ_2}})_* \mathbb{Q}[\dim T]= IC_{M^\circ}|_{D^{\circ}_2} \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathscr{L}_i[\dim \Sigma -2i]. \end{align*} $$
$$ \begin{align*} R (\pi^{\circ}_{T|_{D^\circ_2}})_* \mathbb{Q}[\dim T]= IC_{M^\circ}|_{D^{\circ}_2} \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathscr{L}_i[\dim \Sigma -2i]. \end{align*} $$
By Proposition 3.8.(2) there exists a commutative square

where the horizontal arrows are étale double covers,
![]() $p_2$
is a Zariski locally trivial fibration with fibre
$p_2$
is a Zariski locally trivial fibration with fibre
![]() $I_{2g-3}$
and
$I_{2g-3}$
and
![]() $(\mathbb {C}^*)^{2g, \circ }$
is the complement in
$(\mathbb {C}^*)^{2g, \circ }$
is the complement in
![]() $(\mathbb {C}^*)^{2g}$
of the locus fixed by the involution
$(\mathbb {C}^*)^{2g}$
of the locus fixed by the involution
![]() $v \mapsto v^{-1}$
. Taking cohomology, we write
$v \mapsto v^{-1}$
. Taking cohomology, we write
 $$ \begin{align*} R (\pi^{\circ}_{T|_{D^\circ_2}})_* \mathbb{Q} & = R (\pi^{\circ}_{T|_{D^\circ_2}})_* \circ (Rq^{\prime}_* \mathbb{Q})^+ = (R(\pi^{\circ}_{T|_{D^\circ_2}} \circ q')_* \mathbb{Q})^+ = (R(q \circ p_2)_* \mathbb{Q})^+\\ & = \left(q_* \bigoplus^{4g-7}_{i=0} (\mathbb{Q}_{(\mathbb{C}^*)^{2g, \circ}} \otimes H^{2i}(I_{2g-3}))[-2i]\right)^+\\ & = \bigoplus^{2g-4}_{i=0} \mathbb{Q}_{\Sigma^{\circ}}^{\lceil \frac{i+1}{2}\rceil}[-2i](-i) \oplus \bigoplus^{2g-4}_{i=0} \mathscr{L}^{\lceil \frac{i}{2}\rceil}[- 2 i](-i) \\ & \quad \oplus \bigoplus^{4g-7}_{i=2g-3} \mathbb{Q}_{\Sigma^{\circ}}^{\lceil 2g-3 - \frac{i}{2}\rceil}[-2i](-i) \oplus \bigoplus^{4g-7}_{i=2g-3} \mathscr{L}^{\lceil 2g-3 - \frac{i+1}{2}\rceil}[-2i](-i), \end{align*} $$
$$ \begin{align*} R (\pi^{\circ}_{T|_{D^\circ_2}})_* \mathbb{Q} & = R (\pi^{\circ}_{T|_{D^\circ_2}})_* \circ (Rq^{\prime}_* \mathbb{Q})^+ = (R(\pi^{\circ}_{T|_{D^\circ_2}} \circ q')_* \mathbb{Q})^+ = (R(q \circ p_2)_* \mathbb{Q})^+\\ & = \left(q_* \bigoplus^{4g-7}_{i=0} (\mathbb{Q}_{(\mathbb{C}^*)^{2g, \circ}} \otimes H^{2i}(I_{2g-3}))[-2i]\right)^+\\ & = \bigoplus^{2g-4}_{i=0} \mathbb{Q}_{\Sigma^{\circ}}^{\lceil \frac{i+1}{2}\rceil}[-2i](-i) \oplus \bigoplus^{2g-4}_{i=0} \mathscr{L}^{\lceil \frac{i}{2}\rceil}[- 2 i](-i) \\ & \quad \oplus \bigoplus^{4g-7}_{i=2g-3} \mathbb{Q}_{\Sigma^{\circ}}^{\lceil 2g-3 - \frac{i}{2}\rceil}[-2i](-i) \oplus \bigoplus^{4g-7}_{i=2g-3} \mathscr{L}^{\lceil 2g-3 - \frac{i+1}{2}\rceil}[-2i](-i), \end{align*} $$
where
![]() $\mathscr {L}$
is the rank-1 local system defined in Definition 3.3. Together with Proposition 3.11, we obtain
$\mathscr {L}$
is the rank-1 local system defined in Definition 3.3. Together with Proposition 3.11, we obtain
 $$ \begin{align*} R \pi^{\circ}_{T, *} \mathbb{Q}[\dim T]= IC_{M^\circ} \oplus \bigoplus^{2g-4}_{i=-2g+4}(\mathbb{Q}_{\Sigma^\circ}^{\lceil \frac{2g-3-|i|}{2} \rceil}\oplus \mathscr{L}^{\lfloor \frac{2g-3-|i|}{2} \rfloor})[\dim \Sigma -2i](-2g+3-i). \end{align*} $$
$$ \begin{align*} R \pi^{\circ}_{T, *} \mathbb{Q}[\dim T]= IC_{M^\circ} \oplus \bigoplus^{2g-4}_{i=-2g+4}(\mathbb{Q}_{\Sigma^\circ}^{\lceil \frac{2g-3-|i|}{2} \rceil}\oplus \mathscr{L}^{\lfloor \frac{2g-3-|i|}{2} \rfloor})[\dim \Sigma -2i](-2g+3-i). \end{align*} $$
This splitting holds on
![]() $M^{\circ }$
, and we now extend it through
$M^{\circ }$
, and we now extend it through
![]() $\Omega $
. Note that the defect of semismallness of
$\Omega $
. Note that the defect of semismallness of
![]() $\pi _T$
is
$\pi _T$
is
 $$ \begin{align*} r(\pi_T) & = \dim \pi^{-1}_T(M) \times_{M} \pi^{-1}_T(M) - \dim M \\ & = 2 \dim D_1 - \dim \Omega - \dim M = 6g-8. \end{align*} $$
$$ \begin{align*} r(\pi_T) & = \dim \pi^{-1}_T(M) \times_{M} \pi^{-1}_T(M) - \dim M \\ & = 2 \dim D_1 - \dim \Omega - \dim M = 6g-8. \end{align*} $$
Since
![]() $\Sigma $
is a rational homology manifold,
$\Sigma $
is a rational homology manifold,
![]() $IC_{\Sigma }(\mathbb {Q}_{\Sigma ^\circ }) \simeq \mathbb {Q}_{\Sigma }[\dim \Sigma ]$
. Further, the definition of
$IC_{\Sigma }(\mathbb {Q}_{\Sigma ^\circ }) \simeq \mathbb {Q}_{\Sigma }[\dim \Sigma ]$
. Further, the definition of
![]() $\mathscr {L}$
yields
$\mathscr {L}$
yields
![]() $IC_{\Sigma }(\mathscr {L}) = i_{\Sigma ^\circ ,*}\mathscr {L}[\dim \Sigma ]$
. Therefore, there exists integers
$IC_{\Sigma }(\mathscr {L}) = i_{\Sigma ^\circ ,*}\mathscr {L}[\dim \Sigma ]$
. Therefore, there exists integers
![]() $b(j)$
such that
$b(j)$
such that
 $$ \begin{align*} R\pi_{T, *}\mathbb{Q}[\dim T]= IC_{M} & \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathbb{Q}_{\Sigma}^{\lceil \frac{2g-3-|i|}{2} \rceil}[\dim \Sigma -2i](-2g+3-i) \\ & \oplus \bigoplus^{2g-4}_{i=-2g+4} i_{\Sigma^\circ,*}\mathscr{L}^{\lfloor \frac{2g-3-|i|}{2} \rfloor}[\dim \Sigma-2i](-2g+3-i)\\ & \oplus \bigoplus^{3g-4}_{j=-3g+4} \mathbb{Q}^{b(j)}_{\Omega}[\dim \Omega -2j](-3g+3-j). \end{align*} $$
$$ \begin{align*} R\pi_{T, *}\mathbb{Q}[\dim T]= IC_{M} & \oplus \bigoplus^{2g-4}_{i=-2g+4}\mathbb{Q}_{\Sigma}^{\lceil \frac{2g-3-|i|}{2} \rceil}[\dim \Sigma -2i](-2g+3-i) \\ & \oplus \bigoplus^{2g-4}_{i=-2g+4} i_{\Sigma^\circ,*}\mathscr{L}^{\lfloor \frac{2g-3-|i|}{2} \rfloor}[\dim \Sigma-2i](-2g+3-i)\\ & \oplus \bigoplus^{3g-4}_{j=-3g+4} \mathbb{Q}^{b(j)}_{\Omega}[\dim \Omega -2j](-3g+3-j). \end{align*} $$
Localising at
![]() $x \in \Omega $
, we obtain
$x \in \Omega $
, we obtain
 $$ \begin{align*} \dim H^{2d}(\pi^{-1}_T(x)) = \!\begin{cases} \dim IH^{2d}(N_{\Omega}) + \left\lceil \frac{2g-3-|d-2g+3|}{2} \right\rceil + b(d-3g+3) & \!\!\text{for } 0 \leq d < 4g-6,\\ \dim IH^{2d}(N_{\Omega}) + b(d-3g+3)& \!\text{otherwise}.\\ \end{cases} \end{align*} $$
$$ \begin{align*} \dim H^{2d}(\pi^{-1}_T(x)) = \!\begin{cases} \dim IH^{2d}(N_{\Omega}) + \left\lceil \frac{2g-3-|d-2g+3|}{2} \right\rceil + b(d-3g+3) & \!\!\text{for } 0 \leq d < 4g-6,\\ \dim IH^{2d}(N_{\Omega}) + b(d-3g+3)& \!\text{otherwise}.\\ \end{cases} \end{align*} $$
Therefore,
![]() $b(j)$
is the coefficient of
$b(j)$
is the coefficient of
![]() $q^{d-3g+3}$
of the polynomial
$q^{d-3g+3}$
of the polynomial
 $$ \begin{align*} & E (\pi^{-1}_T(x)) - IE(N_{\Omega}) - \sum^{2g-3}_{i=-2g+3}\left\lceil \frac{2g-3-|i|}{2} \right\rceil q^{2g-3+i} \\ &\quad = \frac{1}{E(\Omega)}(E(D_1)+E(D_3)-E(D_{13})) - IE(N_{\Omega}) - \frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)} \\ &\quad = \frac{\left(1-q^{2g-2}\right) \left(1-q^{2g}\right) \left(1-q^4 -q^{2 g-3}-q^{2g-1}+2q^{2g}\right)}{\left(1-q\right)^3 \left(1-q^2\right)}-\frac{1-q^{2g}}{1-q^2}\\ &\qquad -\frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)}. \end{align*} $$
$$ \begin{align*} & E (\pi^{-1}_T(x)) - IE(N_{\Omega}) - \sum^{2g-3}_{i=-2g+3}\left\lceil \frac{2g-3-|i|}{2} \right\rceil q^{2g-3+i} \\ &\quad = \frac{1}{E(\Omega)}(E(D_1)+E(D_3)-E(D_{13})) - IE(N_{\Omega}) - \frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)} \\ &\quad = \frac{\left(1-q^{2g-2}\right) \left(1-q^{2g}\right) \left(1-q^4 -q^{2 g-3}-q^{2g-1}+2q^{2g}\right)}{\left(1-q\right)^3 \left(1-q^2\right)}-\frac{1-q^{2g}}{1-q^2}\\ &\qquad -\frac{q (1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)}. \end{align*} $$
4.1 Applications of the decomposition theorem
Proof of Theorem 1.3. Taking cohomology with compact support, Theorem 1.2 gives
 $$ \begin{align*} IE(M) & = E(T)- E(\Sigma_{\iota})^+ \cdot \left( \sum^{2g-3}_{i=-2g+3} \left\lceil \frac{2g-3-|i|}{2} \right\rceil q^{2g-3+i}\right)\\ &\quad - E(\Sigma_{\iota})^- \cdot \left(\sum^{2g-3}_{i=-2g+3} \left\lfloor \frac{2g-3-|i|}{2} \right\rfloor q^{2g-3+i} \right)\\ &\quad - E(\pi^{-1}_T(\Omega)) + E(\Omega) \cdot IE(N_{\Omega}) + E(\Omega) \cdot \sum^{2g-3}_{i=-2g+3}\left\lceil \frac{2g-3-|i|}{2} \right\rceil q^{2g-3+i} \\ & = E(M) - E(\Sigma) +E(D^{\circ}_{2})\\ &\quad - (E(\Sigma_{\iota})^+-E(\Omega))\cdot q \frac{(1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)} \\ &\quad - E(\Sigma_{\iota})^- \cdot q^2 \frac{(1 - q^{2 g - 4}) (1 - q^{2 g - 3})}{(1-q) (1-q^2)} +E(\Omega) \cdot IE(N_{\Omega}). \end{align*} $$
$$ \begin{align*} IE(M) & = E(T)- E(\Sigma_{\iota})^+ \cdot \left( \sum^{2g-3}_{i=-2g+3} \left\lceil \frac{2g-3-|i|}{2} \right\rceil q^{2g-3+i}\right)\\ &\quad - E(\Sigma_{\iota})^- \cdot \left(\sum^{2g-3}_{i=-2g+3} \left\lfloor \frac{2g-3-|i|}{2} \right\rfloor q^{2g-3+i} \right)\\ &\quad - E(\pi^{-1}_T(\Omega)) + E(\Omega) \cdot IE(N_{\Omega}) + E(\Omega) \cdot \sum^{2g-3}_{i=-2g+3}\left\lceil \frac{2g-3-|i|}{2} \right\rceil q^{2g-3+i} \\ & = E(M) - E(\Sigma) +E(D^{\circ}_{2})\\ &\quad - (E(\Sigma_{\iota})^+-E(\Omega))\cdot q \frac{(1 - q^{2 g - 3}) (1 - q^{2 g - 2})}{(1-q) (1-q^2)} \\ &\quad - E(\Sigma_{\iota})^- \cdot q^2 \frac{(1 - q^{2 g - 4}) (1 - q^{2 g - 3})}{(1-q) (1-q^2)} +E(\Omega) \cdot IE(N_{\Omega}). \end{align*} $$
Now Proposition 3.8.(2) gives
Therefore, we obtain
 $$ \begin{align*} IE(M)& = E(M) - E(\Sigma) + (E(\Sigma_{\iota})^+-E(\Omega))\cdot \frac{1 - q^{2 g - 2}}{ 1-q^2} \\ &\quad + E(\Sigma_{\iota})^- \cdot q\frac{1 - q^{2 g - 4} }{1-q^2}+ E(\Omega) \cdot \frac{1-q^{2g}}{1-q^2}\\ & = E(M)+ (q^2E(\Sigma_{\iota})^+ + qE(\Sigma_{\iota})^-) \cdot \frac{1 - q^{2 g - 4}}{ 1-q^2} +E(\Omega) \cdot q^{2g-2}.\\[-42pt] \end{align*} $$
$$ \begin{align*} IE(M)& = E(M) - E(\Sigma) + (E(\Sigma_{\iota})^+-E(\Omega))\cdot \frac{1 - q^{2 g - 2}}{ 1-q^2} \\ &\quad + E(\Sigma_{\iota})^- \cdot q\frac{1 - q^{2 g - 4} }{1-q^2}+ E(\Omega) \cdot \frac{1-q^{2g}}{1-q^2}\\ & = E(M)+ (q^2E(\Sigma_{\iota})^+ + qE(\Sigma_{\iota})^-) \cdot \frac{1 - q^{2 g - 4}}{ 1-q^2} +E(\Omega) \cdot q^{2g-2}.\\[-42pt] \end{align*} $$
□
The variant and anti-invariant E-polynomials of
![]() $(\mathbb {C}^*)^{2g}$
and
$(\mathbb {C}^*)^{2g}$
and
![]() $T^*\operatorname {Jac}(C)$
with respect to the involution
$T^*\operatorname {Jac}(C)$
with respect to the involution
![]() $\iota $
defined in Definition 3.3 are
$\iota $
defined in Definition 3.3 are
 $$ \begin{align} E((\mathbb{C}^*)^{2g})^+ & = \sum^{g}_{d=0} \dim (\Lambda^{2d}V) q^{2d}= \frac{1}{2}((1-q)^{2g}+(1+q)^{2g}), \end{align} $$
$$ \begin{align} E((\mathbb{C}^*)^{2g})^+ & = \sum^{g}_{d=0} \dim (\Lambda^{2d}V) q^{2d}= \frac{1}{2}((1-q)^{2g}+(1+q)^{2g}), \end{align} $$
 $$ \begin{align} E((\mathbb{C}^*)^{2g})^- & = -\sum^{g-1}_{d=0} \dim (\Lambda^{2d+1}V) q^{2d+1}= \frac{1}{2}((1-q)^{2g}-(1+q)^{2g}), \end{align} $$
$$ \begin{align} E((\mathbb{C}^*)^{2g})^- & = -\sum^{g-1}_{d=0} \dim (\Lambda^{2d+1}V) q^{2d+1}= \frac{1}{2}((1-q)^{2g}-(1+q)^{2g}), \end{align} $$
 $$ \begin{align} E(T^*\operatorname{Jac}(C))^+ & = \frac{1}{2}(uv)^g \left((1-u)^g(1-v)^g+(1+u)^g(1+v)^g\right), \end{align} $$
$$ \begin{align} E(T^*\operatorname{Jac}(C))^+ & = \frac{1}{2}(uv)^g \left((1-u)^g(1-v)^g+(1+u)^g(1+v)^g\right), \end{align} $$
 $$ \begin{align} E(T^*\operatorname{Jac}(C))^- & = \frac{1}{2}(uv)^g \left((1-u)^g(1-v)^g-(1+u)^g(1+v)^g\right). \end{align} $$
$$ \begin{align} E(T^*\operatorname{Jac}(C))^- & = \frac{1}{2}(uv)^g \left((1-u)^g(1-v)^g-(1+u)^g(1+v)^g\right). \end{align} $$
Proof of Theorem 1.4. We compute
![]() $IE(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
and
$IE(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
and
![]() $IE(M_{\mathrm {B}}(C, \operatorname {GL}_2))$
from (2) by substitution. To this end, recall that
$IE(M_{\mathrm {B}}(C, \operatorname {GL}_2))$
from (2) by substitution. To this end, recall that
![]() $E(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
and
$E(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
and
![]() $E(M_{\mathrm {B}}(C, \operatorname {GL}_2))$
have been computed in [Reference Baraglia and Hekmati4, Theorem 1.3] (equivalently, [Reference Martínez and Muñoz48, Theorem 2]). The E-polynomials of
$E(M_{\mathrm {B}}(C, \operatorname {GL}_2))$
have been computed in [Reference Baraglia and Hekmati4, Theorem 1.3] (equivalently, [Reference Martínez and Muñoz48, Theorem 2]). The E-polynomials of
![]() $\Sigma _{\iota , B}$
and
$\Sigma _{\iota , B}$
and
![]() $\Omega _B$
instead can be determined by using the description of these loci in Proposition 3.2, together with (23) and (24). Further, by (6) we have
$\Omega _B$
instead can be determined by using the description of these loci in Proposition 3.2, together with (23) and (24). Further, by (6) we have
![]() $IE(M_{\mathrm {B}}(C, \operatorname {PGL}_2)) = (1-q)^{-2g} \cdot IE(M_{\mathrm {B}}(C, \operatorname {GL}_2))$
. □
$IE(M_{\mathrm {B}}(C, \operatorname {PGL}_2)) = (1-q)^{-2g} \cdot IE(M_{\mathrm {B}}(C, \operatorname {GL}_2))$
. □
Proof of Theorem 1.8. In view of
we obtain Theorem 1.8 simply by substituting (25) and (26) in (2). □
Proof of Theorem 1.9. The purity of
![]() $IH^*({M}_{\mathrm {Dol}})$
(Proposition 2.4) and the Poincaré duality give
$IH^*({M}_{\mathrm {Dol}})$
(Proposition 2.4) and the Poincaré duality give
Theorem 1.9 then follows from Theorem 1.8 and elementary algebraic manipulations. □
Proof of Theorem 1.12. By the additivity of the E-polynomial, we have
The formula (22), together with (23), (24), (25) and (26), yields
 $$ \begin{align*} E(D^{\circ}_{2, \mathrm{B}}) & = \frac{1-q^{2g-2}}{2(1-q)} \big((1-q^{2g-3})(1-q)^{2g-1} + (1+q^{2g-3})(1+q)^{2g-1}\big)\\ &\quad -2^{2g}\frac{(1-q^{2g-2})^2}{(1-q^2)(1-q)},\\ E(D^{\circ}_{2, \mathrm{Dol}}) & = \frac{1}{2}(uv)^g \frac{1-(uv)^{2g-2}}{1-uv}\bigg( \frac{(1-u)^g(1-v)^g(1-(uv)^{2g-3})}{1-uv} \\ &\quad + \frac{(1+u)^g(1+v)^g(1+(uv)^{2g-3})}{1+uv}\bigg)-2^{2g} \frac{(1-(uv)^{2g-2})^2}{(1-(uv)^2)(1-uv)}, \end{align*} $$
$$ \begin{align*} E(D^{\circ}_{2, \mathrm{B}}) & = \frac{1-q^{2g-2}}{2(1-q)} \big((1-q^{2g-3})(1-q)^{2g-1} + (1+q^{2g-3})(1+q)^{2g-1}\big)\\ &\quad -2^{2g}\frac{(1-q^{2g-2})^2}{(1-q^2)(1-q)},\\ E(D^{\circ}_{2, \mathrm{Dol}}) & = \frac{1}{2}(uv)^g \frac{1-(uv)^{2g-2}}{1-uv}\bigg( \frac{(1-u)^g(1-v)^g(1-(uv)^{2g-3})}{1-uv} \\ &\quad + \frac{(1+u)^g(1+v)^g(1+(uv)^{2g-3})}{1+uv}\bigg)-2^{2g} \frac{(1-(uv)^{2g-2})^2}{(1-(uv)^2)(1-uv)}, \end{align*} $$
and Proposition 3.9 gives
 $$ \begin{align*}E(D_1)+E(D_3)-E(D_{13})=2^{2g}\frac{\left(1-q^{2g-2}\right) \left(1-q^{2g}\right) \left(1-q^4 -q^{2 g-3}-q^{2g-1}+2q^{2g}\right)}{\left(1-q\right)^3 \left(1-q^2\right)}.\\[-42pt] \end{align*} $$
$$ \begin{align*}E(D_1)+E(D_3)-E(D_{13})=2^{2g}\frac{\left(1-q^{2g-2}\right) \left(1-q^{2g}\right) \left(1-q^4 -q^{2 g-3}-q^{2g-1}+2q^{2g}\right)}{\left(1-q\right)^3 \left(1-q^2\right)}.\\[-42pt] \end{align*} $$
□
4.2 From
 $\operatorname {SL}_2$
to
$\operatorname {SL}_2$
to
 $\operatorname {PGL}_2$
or
$\operatorname {PGL}_2$
or
 $\operatorname {GL}_2$
$\operatorname {GL}_2$
In order to compute
![]() $IE({M}_{\mathrm {Dol}}(C, G))$
or
$IE({M}_{\mathrm {Dol}}(C, G))$
or
![]() $IP_t(M(C, G))$
for
$IP_t(M(C, G))$
for
![]() $G=\operatorname {PGL}_2, \operatorname {GL}_2$
, one can repeat the arguments for
$G=\operatorname {PGL}_2, \operatorname {GL}_2$
, one can repeat the arguments for
![]() $\operatorname {SL}_2$
and realise that in practise one can obtain the polynomials for
$\operatorname {SL}_2$
and realise that in practise one can obtain the polynomials for
![]() $\operatorname {PGL}_2$
by replacing the coefficients
$\operatorname {PGL}_2$
by replacing the coefficients
![]() $2^{2g}$
with
$2^{2g}$
with
![]() $1$
in the corresponding polynomials for
$1$
in the corresponding polynomials for
![]() $\operatorname {SL}_2$
, as explained below. Further, one can use (5) and (6) to write the polynomials for
$\operatorname {SL}_2$
, as explained below. Further, one can use (5) and (6) to write the polynomials for
![]() $\operatorname {GL}_2$
from the
$\operatorname {GL}_2$
from the
![]() $\operatorname {PGL}_2$
counterparts.
$\operatorname {PGL}_2$
counterparts.
Definition 4.1.
![]() $\mathrm {Var}^{\Gamma }$
is the category of algebraic varieties endowed with a
$\mathrm {Var}^{\Gamma }$
is the category of algebraic varieties endowed with a
![]() $\Gamma $
-action, with
$\Gamma $
-action, with
![]() $\Gamma $
-equivariant morphisms as morphisms.
$\Gamma $
-equivariant morphisms as morphisms.
![]() $\Gamma \mathrm {-mHs}$
is the abelian category whose objects are
$\Gamma \mathrm {-mHs}$
is the abelian category whose objects are
![]() $\Gamma $
-modules over
$\Gamma $
-modules over
![]() $\mathbb {Q}$
endowed with a mixed Hodge structure and whose morphisms are
$\mathbb {Q}$
endowed with a mixed Hodge structure and whose morphisms are
![]() $\Gamma $
-equivariant morphisms of mixed Hodge structures.
$\Gamma $
-equivariant morphisms of mixed Hodge structures.
Definition 4.2. Let X be an algebraic variety endowed with an algebraic
![]() $\Gamma $
-action. The virtual Hodge realisation of
$\Gamma $
-action. The virtual Hodge realisation of
![]() $(X; \Gamma {\curvearrowright } X)$
is the element in the Groethendieck ring
$(X; \Gamma {\curvearrowright } X)$
is the element in the Groethendieck ring
![]() $K_0(\Gamma \mathrm {-mHs})$
defined by the formula
$K_0(\Gamma \mathrm {-mHs})$
defined by the formula
 $$ \begin{align*}\chi_{\mathrm{Hdg}; \Gamma}(X)=\sum_k (-1)^k [H^k_c(T(C, \operatorname{SL}_2)); \rho_M \colon \Gamma \to \operatorname{Aut}(H^k_c(X))].\end{align*} $$
$$ \begin{align*}\chi_{\mathrm{Hdg}; \Gamma}(X)=\sum_k (-1)^k [H^k_c(T(C, \operatorname{SL}_2)); \rho_M \colon \Gamma \to \operatorname{Aut}(H^k_c(X))].\end{align*} $$
The morphism
 $\chi _{\mathrm {Hdg}; \Gamma }(\cdot )\colon K_0(\mathrm {Var}^{\Gamma }) \to K_0(\Gamma \mathrm {-mHs})$
is additive.
$\chi _{\mathrm {Hdg}; \Gamma }(\cdot )\colon K_0(\mathrm {Var}^{\Gamma }) \to K_0(\Gamma \mathrm {-mHs})$
is additive.
The same Hodge realisation was considered in [Reference Hausel and Thaddeus35, §4], when Hausel and Thaddeus defined E-polynomials with coefficient in the characters of the finite abelian group
![]() $\Gamma $
.
$\Gamma $
.
Now consider the
![]() $\Gamma $
-invariant stratification of
$\Gamma $
-invariant stratification of
![]() ${T}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
whose strata are
${T}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
whose strata are
-
1.
 $S_0 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is stable}\}$
;
$S_0 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is stable}\}$
; -
2.
 $S_1 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \simeq L \oplus L^{-1}, \, L \in \operatorname {Jac}(C), \, L \neq L^{-1}\}$
;
$S_1 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \simeq L \oplus L^{-1}, \, L \in \operatorname {Jac}(C), \, L \neq L^{-1}\}$
; -
3.
 $S_2 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is a nontrivial extension of }L^{-1}\text { by }L \text { for } L\in \operatorname {Jac}(C)\\ \text { with } \, L \neq L^{-1}\}$
;
$S_2 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is a nontrivial extension of }L^{-1}\text { by }L \text { for } L\in \operatorname {Jac}(C)\\ \text { with } \, L \neq L^{-1}\}$
; -
4.
 $S_3 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \simeq L \oplus L, \, L \in \operatorname {Jac}(C)\}$
;
$S_3 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \simeq L \oplus L, \, L \in \operatorname {Jac}(C)\}$
; -
5.
 $S_4 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is a nontrivial extension of }L\text { by }L \text { for } L\in \operatorname {Jac}(C)\}$
;
$S_4 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is a nontrivial extension of }L\text { by }L \text { for } L\in \operatorname {Jac}(C)\}$
; -
6.
 $S_5 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is unstable}\}$
;
$S_5 \simeq \{(E, \phi ) \in {M}_{\mathrm {Dol}}(C, \operatorname {SL}_2) |\, E \text { is unstable}\}$
; -
7.
 $S_6 = D^{\circ }_2$
,
$S_6 = D^{\circ }_2$
,
 $S_7 = D_3 \setminus D_{13}$
and
$S_7 = D_3 \setminus D_{13}$
and
 $S_8 = D_1$
.
$S_8 = D_1$
.
This is indeed a stratification of
![]() ${T}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
, since
${T}_{\mathrm {Dol}}(C, \operatorname {SL}_2)$
, since
 ${M}_{\mathrm {Dol}}(C, \operatorname {SL}_2)^{\text {sm}} = \bigsqcup ^5_{i=0} S_i \simeq {T}_{\mathrm {Dol}}(C, \operatorname {SL}_2) \setminus (D_1 \cup D_2 \cup D_3)$
by [Reference Hitchin37, Example 3.13] and Proposition 3.2. The additivity of the virtual realisation implies that
${M}_{\mathrm {Dol}}(C, \operatorname {SL}_2)^{\text {sm}} = \bigsqcup ^5_{i=0} S_i \simeq {T}_{\mathrm {Dol}}(C, \operatorname {SL}_2) \setminus (D_1 \cup D_2 \cup D_3)$
by [Reference Hitchin37, Example 3.13] and Proposition 3.2. The additivity of the virtual realisation implies that
 $$ \begin{align*}\chi_{\mathrm{Hdg}; \Gamma}({T}_{\mathrm{Dol}}(C, \operatorname{SL}_2))= \sum^8_{i=0} \chi_{\mathrm{Hdg}; \Gamma}(S_i).\end{align*} $$
$$ \begin{align*}\chi_{\mathrm{Hdg}; \Gamma}({T}_{\mathrm{Dol}}(C, \operatorname{SL}_2))= \sum^8_{i=0} \chi_{\mathrm{Hdg}; \Gamma}(S_i).\end{align*} $$
By direct inspection (see [Reference Kiem and Yoo41, §3]) one can check that there exist algebraic varieties
![]() $Z_{ij}$
endowed with a
$Z_{ij}$
endowed with a
![]() $\Gamma $
-action such that
$\Gamma $
-action such that
-
1. the
 $\Gamma $
-module
$\Gamma $
-module
 $H^k_c(Z_{ij})$
is isomorphic to the direct sum of copies of the trivial and of the regular representation of
$H^k_c(Z_{ij})$
is isomorphic to the direct sum of copies of the trivial and of the regular representation of
 $\Gamma $
; that is, there exist integers
$\Gamma $
; that is, there exist integers
 $l_{ijk}$
and
$l_{ijk}$
and
 $m_{ijk}$
such that there exists a
$m_{ijk}$
such that there exists a
 $\Gamma $
-equivariant isomorphism where
$\Gamma $
-equivariant isomorphism where $$ \begin{align*}H^k_c(Z_{ij}) \simeq V^{\oplus n_{ijk}}_{\text{tr}} \oplus V^{\oplus m_{ijk}}_{\text{reg}},\end{align*} $$
$$ \begin{align*}H^k_c(Z_{ij}) \simeq V^{\oplus n_{ijk}}_{\text{tr}} \oplus V^{\oplus m_{ijk}}_{\text{reg}},\end{align*} $$
 $\Gamma $
acts trivially on
$\Gamma $
acts trivially on
 $V_{\text {tr}} \simeq \mathbb {Q}$
and via the regular representation on
$V_{\text {tr}} \simeq \mathbb {Q}$
and via the regular representation on
 $V_{\text {reg}}\simeq \mathbb {Q}^{2^{2g}}$
. We call
$V_{\text {reg}}\simeq \mathbb {Q}^{2^{2g}}$
. We call
 $V^{\oplus m_{ijk}}_{\text {reg}}$
the regular part of
$V^{\oplus m_{ijk}}_{\text {reg}}$
the regular part of
 $H^k_c(Z_{ij})$
.
$H^k_c(Z_{ij})$
.
-
2. we have
where $$ \begin{align*}\chi_{\mathrm{Hdg}; \Gamma}(S_i) = \sum_{j, k} \epsilon_{ij} (-1)^k [H^k_c(Z_{ij}); \rho_{ij}\colon \Gamma \to \operatorname{Aut}(H^k_c(Z_{ij}))],\end{align*} $$
$$ \begin{align*}\chi_{\mathrm{Hdg}; \Gamma}(S_i) = \sum_{j, k} \epsilon_{ij} (-1)^k [H^k_c(Z_{ij}); \rho_{ij}\colon \Gamma \to \operatorname{Aut}(H^k_c(Z_{ij}))],\end{align*} $$
 $\epsilon _{ij}$
is
$\epsilon _{ij}$
is
 $\pm 1$
, and
$\pm 1$
, and
 $\rho _{ij}$
is a direct sum of copies of the trivial and/or of the regular representation.
$\rho _{ij}$
is a direct sum of copies of the trivial and/or of the regular representation.
Denote by
![]() $E_{\text {reg}}(Z_{ij})$
the E-polynomial of the regular part of
$E_{\text {reg}}(Z_{ij})$
the E-polynomial of the regular part of
![]() $H^*_c(Z_{ij})$
, and let
$H^*_c(Z_{ij})$
, and let
![]() $E_{\text {tr}}(Z_{ij}):= E(Z_{ij}) - E_{\text {reg}}(Z_{ij})$
. Then we have
$E_{\text {tr}}(Z_{ij}):= E(Z_{ij}) - E_{\text {reg}}(Z_{ij})$
. Then we have
 $$ \begin{align} E({T}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) & = \sum_{i,j}\epsilon_{ij} E_{\text{tr}}(Z_{ij}) + \sum_{ij}\epsilon_{ij} E_{\text{reg}}(Z_{ij}) \\ & = \sum_{ij}\epsilon_{ij} E_{\text{tr}}(Z_{ij}) + 2^{2g} \sum_{ij}\epsilon_{ij} E_{\text{reg}}(Z_{ij})^{\Gamma} \nonumber \\ E({T}_{\mathrm{Dol}}(C, \operatorname{SL}_2))^{\Gamma} & = \sum_{ij}\epsilon_{ij} E_{\text{tr}}(Z_{ij}) + \sum_{ij}\epsilon_{ij} E_{\text{reg}}(Z_{ij})^{\Gamma}. \nonumber \end{align} $$
$$ \begin{align} E({T}_{\mathrm{Dol}}(C, \operatorname{SL}_2)) & = \sum_{i,j}\epsilon_{ij} E_{\text{tr}}(Z_{ij}) + \sum_{ij}\epsilon_{ij} E_{\text{reg}}(Z_{ij}) \\ & = \sum_{ij}\epsilon_{ij} E_{\text{tr}}(Z_{ij}) + 2^{2g} \sum_{ij}\epsilon_{ij} E_{\text{reg}}(Z_{ij})^{\Gamma} \nonumber \\ E({T}_{\mathrm{Dol}}(C, \operatorname{SL}_2))^{\Gamma} & = \sum_{ij}\epsilon_{ij} E_{\text{tr}}(Z_{ij}) + \sum_{ij}\epsilon_{ij} E_{\text{reg}}(Z_{ij})^{\Gamma}. \nonumber \end{align} $$
Via the decomposition theorem, the same holds for
![]() $IE({M}_{\mathrm {Dol}}(C, \operatorname {SL}_2))$
, and so for
$IE({M}_{\mathrm {Dol}}(C, \operatorname {SL}_2))$
, and so for
![]() $IP_t(M(C, \operatorname {SL}_2))$
, by the purity of
$IP_t(M(C, \operatorname {SL}_2))$
, by the purity of
![]() $IH^*(M(C, \operatorname {SL}_2))$
, as explained in the proof of Theorem 1.9.
$IH^*(M(C, \operatorname {SL}_2))$
, as explained in the proof of Theorem 1.9.
Remark 4.3. Since in our case the varieties
![]() $Z_{ij}$
are completely explicit, we can check that all of the coefficients
$Z_{ij}$
are completely explicit, we can check that all of the coefficients
![]() $2^{2g}$
in Theorem 1.8 come from the E-polynomial of the regular part. So we obtain
$2^{2g}$
in Theorem 1.8 come from the E-polynomial of the regular part. So we obtain
![]() $IE({M}_{\mathrm {Dol}}(C, \operatorname {SL}_2))^{\Gamma }$
by replacing
$IE({M}_{\mathrm {Dol}}(C, \operatorname {SL}_2))^{\Gamma }$
by replacing
![]() $2^{2g}$
by
$2^{2g}$
by
![]() $1$
. By (5) and (6) this gives
$1$
. By (5) and (6) this gives
![]() $IE({M}_{\mathrm {Dol}}(C, G))$
with
$IE({M}_{\mathrm {Dol}}(C, G))$
with
![]() $G=\operatorname {PGL}_2, \operatorname {GL}_2$
. Analogously, knowing
$G=\operatorname {PGL}_2, \operatorname {GL}_2$
. Analogously, knowing
![]() $IP_t(M(C, \operatorname {SL}_2))$
,
$IP_t(M(C, \operatorname {SL}_2))$
,
![]() $E({T}_{\mathrm {Dol}}(C, \operatorname {SL}_2))$
and
$E({T}_{\mathrm {Dol}}(C, \operatorname {SL}_2))$
and
![]() $P_t(T(C, \operatorname {SL}_2))$
, we can write their invariant counterparts, as well as their variants for
$P_t(T(C, \operatorname {SL}_2))$
, we can write their invariant counterparts, as well as their variants for
![]() $G=\operatorname {PGL}_2, \operatorname {GL}_2$
.
$G=\operatorname {PGL}_2, \operatorname {GL}_2$
.
Remark 4.4. By the vanishing of the odd part of
![]() $IH^*_{\mathrm {var}}(M(C, \operatorname {SL}_2))$
(cf. Corollary 1.11), every nontrivial
$IH^*_{\mathrm {var}}(M(C, \operatorname {SL}_2))$
(cf. Corollary 1.11), every nontrivial
 $(\operatorname {Gr}^W_{r+s} IH^d_{\mathrm {var}}(M(C, \operatorname {SL}_2))^{r,s}$
will contribute with nonnegative coefficient to
$(\operatorname {Gr}^W_{r+s} IH^d_{\mathrm {var}}(M(C, \operatorname {SL}_2))^{r,s}$
will contribute with nonnegative coefficient to
![]() $IE_{\mathrm {var}}(M(C, \operatorname {SL}_2))$
. Therefore, there is no cancellation, and the
$IE_{\mathrm {var}}(M(C, \operatorname {SL}_2))$
. Therefore, there is no cancellation, and the
![]() $\Gamma $
-modules
$\Gamma $
-modules
![]() $IH^*(M(C, \operatorname {SL}_2))$
and
$IH^*(M(C, \operatorname {SL}_2))$
and
![]() $H^*(T(C, \operatorname {SL}_2))$
are direct sums of copies of the trivial and of the regular representation of
$H^*(T(C, \operatorname {SL}_2))$
are direct sums of copies of the trivial and of the regular representation of
![]() $\Gamma $
by (27). Comparing with [Reference Daskalopoulos, Wentworth and Wilkin12], one can check that the same holds for
$\Gamma $
by (27). Comparing with [Reference Daskalopoulos, Wentworth and Wilkin12], one can check that the same holds for
![]() $H^*(M(C, \operatorname {SL}_2))$
.
$H^*(M(C, \operatorname {SL}_2))$
.
5 P=W conjectures
5.1 P=W conjecture for twisted character varieties
The computation of E-polynomials of character varieties was initiated in [Reference Hausel and Rodriguez-Villegas33] for twisted character varieties
![]() $M^{\mathrm {tw}}_{\mathrm {B}}=M^{\mathrm {tw}}_{\mathrm {B}}(C,G,d)$
,
$M^{\mathrm {tw}}_{\mathrm {B}}=M^{\mathrm {tw}}_{\mathrm {B}}(C,G,d)$
,

with
![]() $G=\operatorname {GL}_n, \operatorname {SL}_n$
or
$G=\operatorname {GL}_n, \operatorname {SL}_n$
or
![]() $\operatorname {PGL}_n$
and
$\operatorname {PGL}_n$
and
![]() $\mathrm {gcd}(n,d)=1$
; see also [Reference Mereb52].
$\mathrm {gcd}(n,d)=1$
; see also [Reference Mereb52].
As in the untwisted case, a nonabelian Hodge correspondence holds for
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
: there exists a diffeomorphism
$M^{\mathrm {tw}}_{\mathrm {B}}$
: there exists a diffeomorphism
![]() $\Psi \colon M^{\mathrm {tw}}_{\mathrm {Dol}} \to M^{\mathrm {tw}}_{\mathrm {B}}$
, from the Dolbeault moduli space
$\Psi \colon M^{\mathrm {tw}}_{\mathrm {Dol}} \to M^{\mathrm {tw}}_{\mathrm {B}}$
, from the Dolbeault moduli space
![]() $M^{\mathrm {tw}}_{\mathrm {Dol}}=M^{\mathrm {tw}}_{\mathrm {Dol}}(C,G,d)$
of semistable G-Higgs bundles over C of degree d; see [Reference Hausel and Thaddeus36]. However, contrary to the general untwisted character variety,
$M^{\mathrm {tw}}_{\mathrm {Dol}}=M^{\mathrm {tw}}_{\mathrm {Dol}}(C,G,d)$
of semistable G-Higgs bundles over C of degree d; see [Reference Hausel and Thaddeus36]. However, contrary to the general untwisted character variety,
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
is smooth (a significant advantage!).
$M^{\mathrm {tw}}_{\mathrm {B}}$
is smooth (a significant advantage!).
Surprisingly, Hausel and Rodriguez-Villegas [Reference Hausel and Rodriguez-Villegas33] in rank 2, and Mellit [Reference Mellit51] for
![]() $\operatorname {GL}_n$
, observed that the cohomology of
$\operatorname {GL}_n$
, observed that the cohomology of
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
enjoys symmetries typical of smooth projective varieties, despite the fact that
$M^{\mathrm {tw}}_{\mathrm {B}}$
enjoys symmetries typical of smooth projective varieties, despite the fact that
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
is not projective. They called these symmetries curious hard Lefschetz theorem: there exists a class
$M^{\mathrm {tw}}_{\mathrm {B}}$
is not projective. They called these symmetries curious hard Lefschetz theorem: there exists a class
![]() $\alpha \in H^2(M^{\mathrm {tw}}_{\mathrm {B}})$
which induces the isomorphism
$\alpha \in H^2(M^{\mathrm {tw}}_{\mathrm {B}})$
which induces the isomorphism
 $$ \begin{align*} \cup {\alpha^k}\colon \operatorname{Gr}^W_{\dim M_{\mathrm{B}}-2k}H^*(M^{\mathrm{tw}}_{\mathrm{B}})\xrightarrow{\simeq} \operatorname{Gr}^W_{\dim M_{\mathrm{B}}+2k}H^{*+2k}(M^{\mathrm{tw}}_{\mathrm{B}}). \end{align*} $$
$$ \begin{align*} \cup {\alpha^k}\colon \operatorname{Gr}^W_{\dim M_{\mathrm{B}}-2k}H^*(M^{\mathrm{tw}}_{\mathrm{B}})\xrightarrow{\simeq} \operatorname{Gr}^W_{\dim M_{\mathrm{B}}+2k}H^{*+2k}(M^{\mathrm{tw}}_{\mathrm{B}}). \end{align*} $$
Note that, as an immediate consequence of the curious hard Lefschetz theorem, the E-polynomial of
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
is palindromic.
$M^{\mathrm {tw}}_{\mathrm {B}}$
is palindromic.
In the attempt to explain the curious hard Lefschetz theorem, de Cataldo, Hausel and Migliorini conjectured the P=W conjecture, and they verified it for rank 2; see [Reference de Cataldo, Hausel and Migliorini13]. This conjecture posits that the nonabelian Hodge correspondence exchanges two filtrations on the cohomology of
![]() $M^{\mathrm {tw}}_{\mathrm {Dol}}$
and
$M^{\mathrm {tw}}_{\mathrm {Dol}}$
and
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
of very different origin, respectively the perverse Leray filtration (10) associated to the Hitchin fibration
$M^{\mathrm {tw}}_{\mathrm {B}}$
of very different origin, respectively the perverse Leray filtration (10) associated to the Hitchin fibration
![]() $\chi $
on
$\chi $
on
![]() $M^{\mathrm {tw}}_{\mathrm {Dol}}$
(the analogue of the map defined in (11)) and the weight filtration on
$M^{\mathrm {tw}}_{\mathrm {Dol}}$
(the analogue of the map defined in (11)) and the weight filtration on
![]() $M^{\mathrm {tw}}_{\mathrm {B}}$
.
$M^{\mathrm {tw}}_{\mathrm {B}}$
.
Conjecture 5.1 P=W conjecture for twisted moduli spaces
This suggests that the symmetries of the mixed Hodge structure of the cohomology of twisted character varieties, noted by Hausel and Rodriguez-Villegas, should be understood as a manifestation of the standard relative hard Lefschetz symmetries for the proper map
![]() $\chi $
on the Dolbeault side. The latter is an isomorphism between graded pieces of the perverse Leray filtration induced by cup product with a relative
$\chi $
on the Dolbeault side. The latter is an isomorphism between graded pieces of the perverse Leray filtration induced by cup product with a relative
![]() $\chi $
-ample class
$\chi $
-ample class
![]() $\alpha \in H^2(M^{\mathrm {tw}}_{\mathrm {Dol}}(C,G,d))$
:
$\alpha \in H^2(M^{\mathrm {tw}}_{\mathrm {Dol}}(C,G,d))$
:
 $$ \begin{align*} \cup {\alpha^k}\colon \operatorname{Gr}^P_{\dim {M}_{\mathrm{Dol}}/2-k}H^*(M^{\mathrm{tw}}_{\mathrm{Dol}})\xrightarrow{\simeq} \operatorname{Gr}^W_{\dim {M}_{\mathrm{Dol}}/2+2}H^{*+2k}(M^{\mathrm{tw}}_{\mathrm{Dol}}); \end{align*} $$
$$ \begin{align*} \cup {\alpha^k}\colon \operatorname{Gr}^P_{\dim {M}_{\mathrm{Dol}}/2-k}H^*(M^{\mathrm{tw}}_{\mathrm{Dol}})\xrightarrow{\simeq} \operatorname{Gr}^W_{\dim {M}_{\mathrm{Dol}}/2+2}H^{*+2k}(M^{\mathrm{tw}}_{\mathrm{Dol}}); \end{align*} $$
see, for instance, [Reference de Cataldo and Migliorini18, Theorem 2.1.1.(a)].
5.2 PI=WI and the intersection curious hard Lefschetz
In the untwisted (singular) case, curious hard Lefschetz fails in general; for example, [Reference Felisetti and Mauri26, Remark 7.6], and the E-polynomial of
![]() $M_{\mathrm {B}}(C,G)$
is not palindromic; see, for instance, [Reference Logares, Muñoz and Newstead46, Theorem 1.2], [Reference Martínez and Muñoz48, Theorem 2] or [Reference Baraglia and Hekmati4, Theorem 1.3]. In order to restore the symmetries, de Cataldo and Maulik suggested considering the intersection cohomology of
$M_{\mathrm {B}}(C,G)$
is not palindromic; see, for instance, [Reference Logares, Muñoz and Newstead46, Theorem 1.2], [Reference Martínez and Muñoz48, Theorem 2] or [Reference Baraglia and Hekmati4, Theorem 1.3]. In order to restore the symmetries, de Cataldo and Maulik suggested considering the intersection cohomology of
![]() $M_{\mathrm {B}}(C,G)$
, and in [Reference de Cataldo and Maulik15, Question 4.1.7] they conjectured the following.
$M_{\mathrm {B}}(C,G)$
, and in [Reference de Cataldo and Maulik15, Question 4.1.7] they conjectured the following.
Conjecture 5.2 PI=WI conjecture
As in the twisted case, the PI=WI conjecture and the relative hard Lefschetz theorem for
![]() $\chi $
would imply the intersection curious hard Lefschetz theorem.
$\chi $
would imply the intersection curious hard Lefschetz theorem.
Conjecture 5.3 intersection curious hard Lefschetz
There exists a class
![]() $\alpha \in H^2(M_{\mathrm {B}}(C,G))$
which induces the isomorphisms
$\alpha \in H^2(M_{\mathrm {B}}(C,G))$
which induces the isomorphisms
 $$ \begin{align*} \cup {\alpha^k}\colon \operatorname{Gr}^W_{\dim M_{\mathrm{B}}-2k}IH^*(M_{\mathrm{B}}(C,G))\xrightarrow{\simeq} \operatorname{Gr}^W_{\dim M_{\mathrm{B}}+2k}IH^{*+2k}(M_{\mathrm{B}}(C,G)). \end{align*} $$
$$ \begin{align*} \cup {\alpha^k}\colon \operatorname{Gr}^W_{\dim M_{\mathrm{B}}-2k}IH^*(M_{\mathrm{B}}(C,G))\xrightarrow{\simeq} \operatorname{Gr}^W_{\dim M_{\mathrm{B}}+2k}IH^{*+2k}(M_{\mathrm{B}}(C,G)). \end{align*} $$
In particular, the intersection E-polynomial of
![]() $M_{\mathrm {B}}(C,G)$
is palindromic.
$M_{\mathrm {B}}(C,G)$
is palindromic.
In this article we provide some numerical evidence for Conjecture 5.3.
Theorem 5.4 Corollary 1.5
The intersection E-polynomial
![]() $IE(M_{\mathrm {B}}(C,G))$
is palindromic for
$IE(M_{\mathrm {B}}(C,G))$
is palindromic for
![]() $G=\operatorname {GL}_2,\operatorname {SL}_2, \operatorname {PGL}_2$
.
$G=\operatorname {GL}_2,\operatorname {SL}_2, \operatorname {PGL}_2$
.
5.3 PI=WI for
 $\operatorname {SL}_2$
is equivalent to PI=WI for
$\operatorname {SL}_2$
is equivalent to PI=WI for
 $\operatorname {GL}_2$
$\operatorname {GL}_2$
The P=W conjecture for
![]() $\operatorname {SL}_n$
implies the P=W conjectures for
$\operatorname {SL}_n$
implies the P=W conjectures for
![]() $\operatorname {PGL}_n$
and
$\operatorname {PGL}_n$
and
![]() $\operatorname {GL}_n$
; see [Reference Felisetti and Mauri26, §3.3]. The converse holds true in the twisted case for n prime by [Reference de Cataldo, Maulik and Shen17]. By (5) and (6), this reduction boils down to prove the P=W conjecture for the variant cohomology. The proof in Theorem 5.5 does not rely on the smoothness of twisted character varieties, and it extends to the singular case verbatim.
$\operatorname {GL}_n$
; see [Reference Felisetti and Mauri26, §3.3]. The converse holds true in the twisted case for n prime by [Reference de Cataldo, Maulik and Shen17]. By (5) and (6), this reduction boils down to prove the P=W conjecture for the variant cohomology. The proof in Theorem 5.5 does not rely on the smoothness of twisted character varieties, and it extends to the singular case verbatim.
Theorem 5.5 [Reference de Cataldo, Maulik and Shen17]
Suppose that
-
1.
 $ q^{(1-n^2)(2g-2)}IE_{\mathrm {var}}({M}_{\mathrm {Dol}}(C, \operatorname {SL}_n); q,q)=: q^{(1-n^2)(2g-2)}E(q)$
is palindromic;
$ q^{(1-n^2)(2g-2)}IE_{\mathrm {var}}({M}_{\mathrm {Dol}}(C, \operatorname {SL}_n); q,q)=: q^{(1-n^2)(2g-2)}E(q)$
is palindromic; -
2.
 $IE_{\mathrm {var}}(M_{\mathrm {B}}(C, \operatorname {SL}_n); \sqrt {q},\sqrt {q})=q^{(2-n-n^2)(g-1)}E(q)$
.
$IE_{\mathrm {var}}(M_{\mathrm {B}}(C, \operatorname {SL}_n); \sqrt {q},\sqrt {q})=q^{(2-n-n^2)(g-1)}E(q)$
.
Set
![]() $c_n := n(n-1)(g-1)$
. Then we have
$c_n := n(n-1)(g-1)$
. Then we have
 $$ \begin{align*}IH^d_{\mathrm{var}}(M(C, \operatorname{SL}_n)) \simeq \operatorname{Gr}^P_{d-c_n} IH^d_{\mathrm{var}}({M}_{\mathrm{Dol}}(C, \operatorname{SL}_n)) \simeq \operatorname{Gr}^W_{2(d-c_n)} IH^d_{\mathrm{var}}(M_{\mathrm{B}}(C, \operatorname{SL}_n)).\end{align*} $$
$$ \begin{align*}IH^d_{\mathrm{var}}(M(C, \operatorname{SL}_n)) \simeq \operatorname{Gr}^P_{d-c_n} IH^d_{\mathrm{var}}({M}_{\mathrm{Dol}}(C, \operatorname{SL}_n)) \simeq \operatorname{Gr}^W_{2(d-c_n)} IH^d_{\mathrm{var}}(M_{\mathrm{B}}(C, \operatorname{SL}_n)).\end{align*} $$
Unfortunately, in the untwisted case the variant intersection E-polynomials are available only in rank 2; see Corollary 1.11.
Corollary 5.6. The PI=WI conjecture for
![]() $M(C,\operatorname {SL}_2)$
is equivalent to the PI=WI conjecture for
$M(C,\operatorname {SL}_2)$
is equivalent to the PI=WI conjecture for
![]() $M(C,\operatorname {GL}_2)$
.
$M(C,\operatorname {GL}_2)$
.
5.4 Tautological classes
In [Reference Hausel and Thaddeus35] Hausel and Thaddeus proved that
![]() $H^*(M^{\mathrm {tw}}(C, \operatorname {SL}_2))^{\Gamma }$
is generated by tautological classes.Footnote
8
This is an essential ingredient of the proof of the P=W conjecture in the twisted case [Reference de Cataldo, Hausel and Migliorini13] and [Reference de Cataldo, Maulik and Shen16] and a missing desirable piece of information in the untwisted case. Here we provide a partial result: we show that tautological classes do generate the low-degree intersection cohomology of M.
$H^*(M^{\mathrm {tw}}(C, \operatorname {SL}_2))^{\Gamma }$
is generated by tautological classes.Footnote
8
This is an essential ingredient of the proof of the P=W conjecture in the twisted case [Reference de Cataldo, Hausel and Migliorini13] and [Reference de Cataldo, Maulik and Shen16] and a missing desirable piece of information in the untwisted case. Here we provide a partial result: we show that tautological classes do generate the low-degree intersection cohomology of M.
Let
![]() $B(C, \operatorname {SL}_2)$
be the (infinite-dimensional and contractible) space of
$B(C, \operatorname {SL}_2)$
be the (infinite-dimensional and contractible) space of
![]() $\operatorname {SL}_2$
-Higgs bundles on C of degree zero and
$\operatorname {SL}_2$
-Higgs bundles on C of degree zero and
![]() $B^{ss}(C, \operatorname {SL}_2)$
be the corresponding locus of semistable Higgs bundles. Let
$B^{ss}(C, \operatorname {SL}_2)$
be the corresponding locus of semistable Higgs bundles. Let
![]() $\mathcal {G}$
be the group of real gauge transformations with fixed determinant acting on this spaces by precomposition and
$\mathcal {G}$
be the group of real gauge transformations with fixed determinant acting on this spaces by precomposition and
![]() $\mathcal {G}^{\mathbb {C}}$
its complexification.
$\mathcal {G}^{\mathbb {C}}$
its complexification.
We can identify the classifying space
![]() $B\mathcal {G} \simeq B(C, \operatorname {SL}_2)$
with the space of continuous maps
$B\mathcal {G} \simeq B(C, \operatorname {SL}_2)$
with the space of continuous maps
![]() $\operatorname {Map}(C, \operatorname {SU}_2)$
. The second Chern class of the tautological (flat)
$\operatorname {Map}(C, \operatorname {SU}_2)$
. The second Chern class of the tautological (flat)
![]() $\operatorname {SU}_2$
-bundle
$\operatorname {SU}_2$
-bundle
![]() $\mathcal {T}$
on
$\mathcal {T}$
on
![]() $C \times \operatorname {Map}(C, \operatorname {SU}_2)$
admits the Künneth decomposition
$C \times \operatorname {Map}(C, \operatorname {SU}_2)$
admits the Künneth decomposition
 $$ \begin{align*} c_2(\mathcal{T})= \sigma \otimes \alpha + \sum^{2g}_{j=1} e_j \otimes \psi_j + 1 \otimes \beta, \end{align*} $$
$$ \begin{align*} c_2(\mathcal{T})= \sigma \otimes \alpha + \sum^{2g}_{j=1} e_j \otimes \psi_j + 1 \otimes \beta, \end{align*} $$
where
![]() $\sigma \in H^2(C)$
is the fundamental cohomology class, and
$\sigma \in H^2(C)$
is the fundamental cohomology class, and
![]() $e_1, \ldots , e_{2g}$
is a standard symplectic basis of
$e_1, \ldots , e_{2g}$
is a standard symplectic basis of
![]() $H^1(C)$
. Atiyah and Bott showed in [Reference Atiyah and Bott3] that the rational cohomology of
$H^1(C)$
. Atiyah and Bott showed in [Reference Atiyah and Bott3] that the rational cohomology of
![]() $B\mathcal {G}$
is freely generated by the tautological classes
$B\mathcal {G}$
is freely generated by the tautological classes
![]() $\alpha $
,
$\alpha $
,
![]() $\psi _j$
and
$\psi _j$
and
![]() $\beta $
. That is,
$\beta $
. That is,
![]() $H^*(B\mathcal {G})$
is the tensor product of the polynomial algebra on the classes
$H^*(B\mathcal {G})$
is the tensor product of the polynomial algebra on the classes
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
of degree 2 and 4 with an exterior algebra on the classes
$\beta $
of degree 2 and 4 with an exterior algebra on the classes
![]() $\psi _j$
of degree 3,
$\psi _j$
of degree 3,
In particular, the Poincaré polynomial of the classifying space
![]() $B\mathcal {G}$
is
$B\mathcal {G}$
is
 $$ \begin{align} P_t(B\mathcal{G})=\frac{(t^3+1)^{2g}}{(t^2-1)(t^4-1)}. \end{align} $$
$$ \begin{align} P_t(B\mathcal{G})=\frac{(t^3+1)^{2g}}{(t^2-1)(t^4-1)}. \end{align} $$
Now the nonabelian Hodge correspondence induces the following isomorphism in equivariant cohomology:
see [Reference Daskalopoulos, Wentworth and Wilkin12, Theorem 1.2]. Together with Kirwan surjectivity, [Reference Daskalopoulos, Weitsman, Wentworth and Wilkin10, Theorem 1.4]
 $$ \begin{align} H^{*}(B\mathcal{G})\simeq H^{*}_{\mathcal{G}}(B(C, \operatorname{SL}_2)) \twoheadrightarrow H^{*}_{\mathcal{G}}(B^{ss}(C, \operatorname{SL}_2))^{\Gamma}, \end{align} $$
$$ \begin{align} H^{*}(B\mathcal{G})\simeq H^{*}_{\mathcal{G}}(B(C, \operatorname{SL}_2)) \twoheadrightarrow H^{*}_{\mathcal{G}}(B^{ss}(C, \operatorname{SL}_2))^{\Gamma}, \end{align} $$
this implies that the
![]() $\Gamma $
-invariant
$\Gamma $
-invariant
![]() $\operatorname {SL}_2$
-equivariant cohomology of
$\operatorname {SL}_2$
-equivariant cohomology of
![]() $\operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)$
is generated by tautological classes.
$\operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)$
is generated by tautological classes.
Theorem 5.7.
![]() $IH^{< 4g-6}(M(C, \operatorname {SL}_2))$
has a canonical structure of graded ring freely generated by the tautological classes
$IH^{< 4g-6}(M(C, \operatorname {SL}_2))$
has a canonical structure of graded ring freely generated by the tautological classes
![]() $\alpha $
,
$\alpha $
,
![]() $\psi _j$
,
$\psi _j$
,
![]() $\beta $
of degree 2, 3, 4, respectively, and weight 4. Among the tautological classes, only
$\beta $
of degree 2, 3, 4, respectively, and weight 4. Among the tautological classes, only
![]() $\alpha $
is a cohomology class; that is, it is in the image of the natural map
$\alpha $
is a cohomology class; that is, it is in the image of the natural map
![]() $H^*(M(C, \operatorname {SL}_2)) \to IH^*(M(C, \operatorname {SL}_2))$
.
$H^*(M(C, \operatorname {SL}_2)) \to IH^*(M(C, \operatorname {SL}_2))$
.
Proof. Since
![]() $\Sigma $
has codimension
$\Sigma $
has codimension
![]() $4g-6$
in M, we have
$4g-6$
in M, we have
see, for instance, [Reference Durfee23, Lemma 1]. In particular,
![]() $IH^{<4g-6}(M(C, \operatorname {SL}_2))$
has a natural structure of graded ring. The open subset of simple representations
$IH^{<4g-6}(M(C, \operatorname {SL}_2))$
has a natural structure of graded ring. The open subset of simple representations
![]() $\operatorname {Hom}^{s}(\pi _1(C), \operatorname {SL}_2)$
in
$\operatorname {Hom}^{s}(\pi _1(C), \operatorname {SL}_2)$
in
![]() $\operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)$
is a
$\operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)$
is a
![]() $\operatorname {PGL}_2$
-principal bundle over the smooth locus
$\operatorname {PGL}_2$
-principal bundle over the smooth locus
![]() $M^{\mathrm {sm}}_B(C, \operatorname {SL}_2)$
, and so
$M^{\mathrm {sm}}_B(C, \operatorname {SL}_2)$
, and so
We claim that the composition of (31), (30), (34), the inverse of (33) and (32),
 $$ \begin{align*} H^{<4g-6}(B \mathcal{G}) & \xrightarrow{a} H^{<4g-6}_{\operatorname{SL}_2} (\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)) \\ & \xrightarrow{b} H^{<4g-6}_{\operatorname{SL}_2} (\operatorname{Hom}^s(\pi_1(C), \operatorname{SL}_2))\simeq IH^{< 4g-6}(M(C, \operatorname{SL}_2)), \end{align*} $$
$$ \begin{align*} H^{<4g-6}(B \mathcal{G}) & \xrightarrow{a} H^{<4g-6}_{\operatorname{SL}_2} (\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)) \\ & \xrightarrow{b} H^{<4g-6}_{\operatorname{SL}_2} (\operatorname{Hom}^s(\pi_1(C), \operatorname{SL}_2))\simeq IH^{< 4g-6}(M(C, \operatorname{SL}_2)), \end{align*} $$
is an isomorphism. Indeed, a is surjective by (31) (and Corollary 1.11) and actually bijective since by [Reference Daskalopoulos and Uhlenbeck11, Corollary 1.3] we have
 $$ \begin{align*} P^{\operatorname{SL}_2}_t(\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)):= \sum_d \dim H^d_{\operatorname{SL}_2}(\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2))t^d = P_t(B\mathcal{G}) + O(t^{4g-4}). \end{align*} $$
$$ \begin{align*} P^{\operatorname{SL}_2}_t(\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)):= \sum_d \dim H^d_{\operatorname{SL}_2}(\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2))t^d = P_t(B\mathcal{G}) + O(t^{4g-4}). \end{align*} $$
Further, b is injective by Lemma 5.9 and actually bijective due to (3) and (29). The free generation of
![]() $IH^{<4g-6}(M(C, \operatorname {SL}_2))$
now follows from (28). See [Reference Shende64] for the weight of the tautological classes. Finally,
$IH^{<4g-6}(M(C, \operatorname {SL}_2))$
now follows from (28). See [Reference Shende64] for the weight of the tautological classes. Finally,
![]() $\psi _i$
and
$\psi _i$
and
![]() $\beta $
are not cohomology classes by Corollary 1.10 and preceding lines.
$\beta $
are not cohomology classes by Corollary 1.10 and preceding lines.
Remark 5.8.
Theorem 5.7 holds for
![]() $\operatorname {PGL}_2$
, as
$\operatorname {PGL}_2$
, as
by Corollary 1.11, and so for
![]() $\operatorname {GL}_2$
, too. In the latter case, however, mind that there are additional generators
$\operatorname {GL}_2$
, too. In the latter case, however, mind that there are additional generators
![]() $\epsilon _j$
which are pullback via the map (4) of a standard basis of
$\epsilon _j$
which are pullback via the map (4) of a standard basis of
![]() $H^1(M(C,\operatorname {GL}_1))\simeq H^1(C)$
.
$H^1(M(C,\operatorname {GL}_1))\simeq H^1(C)$
.
As a final remark, note that the proof of Theorem 5.7 shows the more general statement that Kirwan surjectivity implies the tautological generation of the low-degree intersection cohomology for
![]() $M(C, \operatorname {SL}_n)$
. However, this surjectivity is an open problem for
$M(C, \operatorname {SL}_n)$
. However, this surjectivity is an open problem for
![]() $n>2$
; cf. [Reference Cliff, Nevins and Shen9].
$n>2$
; cf. [Reference Cliff, Nevins and Shen9].
We prove the lemma used in the proof of Theorem 5.7.
Lemma 5.9. The natural restriction map
 $$ \begin{align} H^d_{\operatorname{SL}_2} (\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)) \to H^d_{\operatorname{SL}_2} (\operatorname{Hom}^s(\pi_1(C), \operatorname{SL}_2)) \end{align} $$
$$ \begin{align} H^d_{\operatorname{SL}_2} (\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)) \to H^d_{\operatorname{SL}_2} (\operatorname{Hom}^s(\pi_1(C), \operatorname{SL}_2)) \end{align} $$
is bijective for
![]() $d<4g-7$
and injective for
$d<4g-7$
and injective for
![]() $d=4g-7$
.
$d=4g-7$
.
Proof. Set
![]() $c := \operatorname {codim}\operatorname {Sing} \operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)=\dim M - \dim \Sigma + \dim \operatorname {Stab}_\Sigma = 4g-5$
, where
$c := \operatorname {codim}\operatorname {Sing} \operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)=\dim M - \dim \Sigma + \dim \operatorname {Stab}_\Sigma = 4g-5$
, where
![]() $\operatorname {Stab}_\Sigma \simeq \mathbb {G}_m$
is the stabiliser of a closed orbit over
$\operatorname {Stab}_\Sigma \simeq \mathbb {G}_m$
is the stabiliser of a closed orbit over
![]() $\Sigma $
. Since
$\Sigma $
. Since
![]() $\operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)$
is a complete intersection (adapt [Reference Etingof24, Theorem 1.2] or [Reference Simpson66, Proposition 11.3]), there exists an isomorphism
$\operatorname {Hom}(\pi _1(C), \operatorname {SL}_2)$
is a complete intersection (adapt [Reference Etingof24, Theorem 1.2] or [Reference Simpson66, Proposition 11.3]), there exists an isomorphism
 $$ \begin{align} H^d_{\operatorname{SL}_2} (\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)) \simeq H^d_{\operatorname{SL}_2} (\operatorname{Hom}^{\mathrm{sm}}(\pi_1(C), \operatorname{SL}_2)) \text{ for }d<c-1. \end{align} $$
$$ \begin{align} H^d_{\operatorname{SL}_2} (\operatorname{Hom}(\pi_1(C), \operatorname{SL}_2)) \simeq H^d_{\operatorname{SL}_2} (\operatorname{Hom}^{\mathrm{sm}}(\pi_1(C), \operatorname{SL}_2)) \text{ for }d<c-1. \end{align} $$
Indeed, take an approximation
![]() $E_k$
of the universal
$E_k$
of the universal
![]() $\operatorname {SL}_2$
-bundle
$\operatorname {SL}_2$
-bundle
![]() $E\mathrm {SL}_2$
; that is, a smooth variety
$E\mathrm {SL}_2$
; that is, a smooth variety
![]() $E_k$
with a free
$E_k$
with a free
![]() $\operatorname {SL}_2$
-action and such that
$\operatorname {SL}_2$
-action and such that
 $H^{< k}(X \times _{\operatorname {SL}_2}E_k)\simeq H^{< k}_{\operatorname {SL}_2}(X \times _{\operatorname {SL}_2}E\mathrm {SL}_2)=: H^{< k}_{\operatorname {SL}_2}(X);$
see [Reference Anderson1, Lemma 1.3]. By Luna slice theorem
$H^{< k}(X \times _{\operatorname {SL}_2}E_k)\simeq H^{< k}_{\operatorname {SL}_2}(X \times _{\operatorname {SL}_2}E\mathrm {SL}_2)=: H^{< k}_{\operatorname {SL}_2}(X);$
see [Reference Anderson1, Lemma 1.3]. By Luna slice theorem
![]() $X \times _{\operatorname {SL}_2}E_k$
is a local complete intersection, and the singular locus has again codimension c. Then (35) follows from [Reference Goresky and MacPherson31, p.199].
$X \times _{\operatorname {SL}_2}E_k$
is a local complete intersection, and the singular locus has again codimension c. Then (35) follows from [Reference Goresky and MacPherson31, p.199].
Further, the complement of
![]() $\operatorname {Hom}^s(\pi _1(C), \operatorname {SL}_2)$
in the smooth locus has codimension
$\operatorname {Hom}^s(\pi _1(C), \operatorname {SL}_2)$
in the smooth locus has codimension
![]() $2g-3$
; see, for instance, [Reference González-Prieto29, §7.2] where the complement is denoted
$2g-3$
; see, for instance, [Reference González-Prieto29, §7.2] where the complement is denoted
![]() $\mathfrak {X}^{\rho }_{g}$
. Therefore, by the equivariant Thom isomorphism, the restriction map
$\mathfrak {X}^{\rho }_{g}$
. Therefore, by the equivariant Thom isomorphism, the restriction map
 $$ \begin{align*}H^d_{\operatorname{SL}_2} (\operatorname{Hom}^{\mathrm{sm}}(\pi_1(C), \operatorname{SL}_2)) \to H^d_{\operatorname{SL}_2} (\operatorname{Hom}^{s}(\pi_1(C), \operatorname{SL}_2))\end{align*} $$
$$ \begin{align*}H^d_{\operatorname{SL}_2} (\operatorname{Hom}^{\mathrm{sm}}(\pi_1(C), \operatorname{SL}_2)) \to H^d_{\operatorname{SL}_2} (\operatorname{Hom}^{s}(\pi_1(C), \operatorname{SL}_2))\end{align*} $$
is bijective for
![]() $d<4g-7$
and injective for
$d<4g-7$
and injective for
![]() $d=4g-7$
.
$d=4g-7$
.
5.5 P=W vs PI=WI: nonpurity of
 $H^*(M_{\mathrm {B}})$
$H^*(M_{\mathrm {B}})$
Despite the failure of curious hard Lefschetz, it still makes sense to conjecture
![]() $P=W$
phenomena for the ordinary cohomology of
$P=W$
phenomena for the ordinary cohomology of
![]() $M_{\mathrm {B}}$
.
$M_{\mathrm {B}}$
.
Conjecture 5.10 P=W conjecture for untwisted character varieties
It was proved in [Reference Felisetti and Mauri26, Theorem 6.1] that the PI=WI conjecture for genus 2 and rank 2 implies the P=W conjecture simply by restriction, since
![]() $H^*(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
injects into
$H^*(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
injects into
![]() $IH^*(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
or, equivalently, by the purity of
$IH^*(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
or, equivalently, by the purity of
![]() $H^*(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
; see Proposition 2.4. In higher genus the situation is more subtle, as the following theorem shows.
$H^*(M_{\mathrm {B}}(C, \operatorname {SL}_2))$
; see Proposition 2.4. In higher genus the situation is more subtle, as the following theorem shows.
Theorem 5.11. Let C be a curve of genus
![]() $g>3$
. Then the natural map
$g>3$
. Then the natural map
![]() $H^*(M) \to IH^*(M)$
is not injective. Equivalently,
$H^*(M) \to IH^*(M)$
is not injective. Equivalently,
![]() ${M}_{\mathrm {Dol}}$
has no pure cohomology.
${M}_{\mathrm {Dol}}$
has no pure cohomology.
Proof. Otherwise, the polynomial
![]() $IP_t(M)-P_t(M)$
would have only positive coefficients, but this is not the case by Corollary 1.10 and preceding lines.
$IP_t(M)-P_t(M)$
would have only positive coefficients, but this is not the case by Corollary 1.10 and preceding lines.
Remark 5.12 Torelli group
We propose an alternative proof of Theorem 5.11. The Torelli group is the subgroup of the mapping class group acting trivially on the cohomology of the curve C. The Torelli group acts nontrivially on
![]() $H^*(M)$
by [Reference Daskalopoulos, Wentworth and Wilkin12, Proposition 4.7] (already in degree
$H^*(M)$
by [Reference Daskalopoulos, Wentworth and Wilkin12, Proposition 4.7] (already in degree
![]() $6$
by [Reference Cappell, Lee and Miller7, Theorem 1.1]), but
$6$
by [Reference Cappell, Lee and Miller7, Theorem 1.1]), but
![]() $IH^{<4g-6}(M)$
is generated by tautological classes due to Theorem 5.7, and so the Torelli group acts trivially on
$IH^{<4g-6}(M)$
is generated by tautological classes due to Theorem 5.7, and so the Torelli group acts trivially on
![]() $IH^{<4g-6}(M)$
as in [Reference Cappell, Lee and Miller7, Theorem 2.1.(c)]. Since the natural map
$IH^{<4g-6}(M)$
as in [Reference Cappell, Lee and Miller7, Theorem 2.1.(c)]. Since the natural map
![]() $H^*(M) \to IH^*(M)$
is equivariant with respect to the Torelli group, we conclude that it has nontrivial kernel for
$H^*(M) \to IH^*(M)$
is equivariant with respect to the Torelli group, we conclude that it has nontrivial kernel for
![]() $g>3$
.
$g>3$
.
5.6 P=W for resolution fails when no symplectic resolution exists
In [Reference Felisetti and Mauri26] Camilla Felisetti and the author proposed a strong version of PI=WI conjecture, called P=W for resolution, and proved it for character varieties which admit a symplectic resolution.
Conjecture 5.13 P=W conjecture for resolution
There exist resolutions of singularities
 $f_{\mathrm {Dol}}\colon \widetilde {M}_{\mathrm {Dol}}(C,G) \to {M}_{\mathrm {Dol}}(C,G)$
and
$f_{\mathrm {Dol}}\colon \widetilde {M}_{\mathrm {Dol}}(C,G) \to {M}_{\mathrm {Dol}}(C,G)$
and
 $f_{\mathrm {B}}\colon \widetilde {M}_{\mathrm {B}}(C,G) \to {M}_{\mathrm {B}}(C,G)$
and a diffeomorphism
$f_{\mathrm {B}}\colon \widetilde {M}_{\mathrm {B}}(C,G) \to {M}_{\mathrm {B}}(C,G)$
and a diffeomorphism
 $\widetilde {\Psi }\colon \widetilde {M}_{\mathrm {Dol}}(C,G) \to \widetilde {M}_{\mathrm {B}}(C,G)$
, such that the following square commutes:
$\widetilde {\Psi }\colon \widetilde {M}_{\mathrm {Dol}}(C,G) \to \widetilde {M}_{\mathrm {B}}(C,G)$
, such that the following square commutes:

and the lift
![]() $\widetilde {\Psi }^*$
of the nonabelian Hodge correspondence
$\widetilde {\Psi }^*$
of the nonabelian Hodge correspondence
![]() ${\Psi }^*$
satisfies the property
${\Psi }^*$
satisfies the property
 $$ \begin{align} P_kH^*(\widetilde{M}_{\mathrm{Dol}}(C,G), \mathbb{Q}) = \widetilde{\Psi}^* W_{2k}H^*(\widetilde{M}_{\mathrm{B}}(C,G), \mathbb{Q}). \end{align} $$
$$ \begin{align} P_kH^*(\widetilde{M}_{\mathrm{Dol}}(C,G), \mathbb{Q}) = \widetilde{\Psi}^* W_{2k}H^*(\widetilde{M}_{\mathrm{B}}(C,G), \mathbb{Q}). \end{align} $$
In [Reference Felisetti and Mauri26, Theorem 3.4] Camilla Felisetti and the author proved that resolutions of singularities satisfying (36) do exist; for instance, the Kirwan–O’Grady desingularisations are such.
In Theorem 5.14 we show, however, that if
![]() $M(C,\operatorname {GL}_n)$
does not admit a symplectic resolution, no resolution of
$M(C,\operatorname {GL}_n)$
does not admit a symplectic resolution, no resolution of
![]() $M(C,\operatorname {GL}_n)$
satisfies (37), despite the palindromicity of the E-polynomial of
$M(C,\operatorname {GL}_n)$
satisfies (37), despite the palindromicity of the E-polynomial of
![]() $T_B$
; see Theorem 1.12. A fortiori, the same negative result holds for
$T_B$
; see Theorem 1.12. A fortiori, the same negative result holds for
![]() $G=\operatorname {SL}_n$
.
$G=\operatorname {SL}_n$
.
This means that the hypotheses of [Reference Felisetti25, Main Theorem, 3] were optimal for
![]() $G=\operatorname {GL}_n, \operatorname {SL}_n$
: the proof of Theorem 5.14 suggests that the semismallness of the desingularisation may be a necessary requirement for the P=W conjecture for resolutions to hold for a G-character variety with G arbitrary reductive group. This is compatible with the expectation of [Reference de Cataldo, Hausel and Migliorini14, §4.4].
$G=\operatorname {GL}_n, \operatorname {SL}_n$
: the proof of Theorem 5.14 suggests that the semismallness of the desingularisation may be a necessary requirement for the P=W conjecture for resolutions to hold for a G-character variety with G arbitrary reductive group. This is compatible with the expectation of [Reference de Cataldo, Hausel and Migliorini14, §4.4].
Theorem 5.14. Let
![]() $M(C, \operatorname {GL}_n)$
be an untwisted
$M(C, \operatorname {GL}_n)$
be an untwisted
![]() $\operatorname {GL}_n$
-character variety with no symplectic resolution; that is, for
$\operatorname {GL}_n$
-character variety with no symplectic resolution; that is, for
![]() $g,n>1$
and
$g,n>1$
and
![]() $(g,n)\neq (2,2)$
. Then the P=W conjecture for any resolution of
$(g,n)\neq (2,2)$
. Then the P=W conjecture for any resolution of
![]() $M(C, \operatorname {GL}_n)$
does not hold.
$M(C, \operatorname {GL}_n)$
does not hold.
Proof. Let
 $f\colon \widetilde {M} \to M(C, \operatorname {GL}_n)$
be a resolution of singularities of
$f\colon \widetilde {M} \to M(C, \operatorname {GL}_n)$
be a resolution of singularities of
![]() $M(C, \operatorname {GL}_n)$
as in (36) and E be an f-exceptional divisor whose image is contained in the singular locus
$M(C, \operatorname {GL}_n)$
as in (36) and E be an f-exceptional divisor whose image is contained in the singular locus
![]() $\Sigma := \operatorname {Sing} M(C, \operatorname {GL}_n)$
. Recall that
$\Sigma := \operatorname {Sing} M(C, \operatorname {GL}_n)$
. Recall that
 $\chi \colon {M}_{\mathrm {Dol}}(C, \operatorname {GL}_n) \to \Lambda := \bigoplus ^n_{i=1} H^0(C, K^{\otimes i}_C)$
is the Hitchin fibration (11).
$\chi \colon {M}_{\mathrm {Dol}}(C, \operatorname {GL}_n) \to \Lambda := \bigoplus ^n_{i=1} H^0(C, K^{\otimes i}_C)$
is the Hitchin fibration (11).
The locus
![]() $\chi (\Sigma )$
consists of reducible characteristic polynomials, and it has codimension
$\chi (\Sigma )$
consists of reducible characteristic polynomials, and it has codimension
 $$ \begin{align*} \frac{1}{2}(\dim M(C, \operatorname{GL}_n) - \max\{\dim M(C, \operatorname{GL}_{n_1})+\dim M(C, \operatorname{GL}_{n_2}): n=n_1+n_2\}) \geq 2. \end{align*} $$
$$ \begin{align*} \frac{1}{2}(\dim M(C, \operatorname{GL}_n) - \max\{\dim M(C, \operatorname{GL}_{n_1})+\dim M(C, \operatorname{GL}_{n_2}): n=n_1+n_2\}) \geq 2. \end{align*} $$
The last inequality follows, for instance, from [Reference Bellamy and Schedler6, Lemma 2.2.(2)]. In particular, the general affine line in
![]() $\Lambda $
avoids
$\Lambda $
avoids
![]() $\chi \circ f(E) \subseteq \chi (\Sigma )$
. Then by (10) the Poincaré dual of E belongs to
$\chi \circ f(E) \subseteq \chi (\Sigma )$
. Then by (10) the Poincaré dual of E belongs to
 $P_0 H^2(\widetilde {M})$
. However, since
$P_0 H^2(\widetilde {M})$
. However, since
![]() $\widetilde {M}_{\mathrm {B}}$
is smooth,
$\widetilde {M}_{\mathrm {B}}$
is smooth,
 $H^2(\widetilde {M}_B)$
has weight not smaller than 2. This contradicts (37).
$H^2(\widetilde {M}_B)$
has weight not smaller than 2. This contradicts (37).
Acknowledgements
I would like to acknowledge useful conversations and email exchanges with Mark de Cataldo, Camilla Felisetti, Tamas Hausel, Daniel Huybrechts, Young-Hoon Kiem, Luca Migliorini, Hiraku Nakajima, Giulia Saccà, Travis Schedler and Richard Wentworth. I am also grateful to the anonymous referee for helpful comments. This work was supported by the Max Planck Institute for Mathematics.
Competing Interest
None.