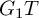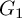1 Introduction
Let G be a connected reductive algebraic group over an algebraically closed field
![]() ${\mathbb {K}}$
of characteristic
${\mathbb {K}}$
of characteristic
![]() $p> 0$
. One of the most important goals in representation theory is to describe the characters of irreducible representations. In the case of rational representations of G, Lusztig gave a conjecture which gives the characters of irreducible representations of G in terms of Kazhdan-Lusztig polynomials of the affine Weyl group for
$p> 0$
. One of the most important goals in representation theory is to describe the characters of irreducible representations. In the case of rational representations of G, Lusztig gave a conjecture which gives the characters of irreducible representations of G in terms of Kazhdan-Lusztig polynomials of the affine Weyl group for
![]() $p> h$
, where h is the Coxeter number. Thanks to the works of Kazhdan-Lusztig [Reference Kazhdan and LusztigKL93, Reference Kazhdan and LusztigKL94a, Reference Kazhdan and LusztigKL94b], Kashiwara-Tanisaki [Reference Kashiwara and TanisakiKT95, Reference Kashiwara and TanisakiKT96] and Andersen-Jantzen-Soergel [Reference Andersen, Jantzen and SoergelAJS94], this is proved for p large enough. An explicit bound on p is known by Fiebig [Reference FiebigFie12].
$p> h$
, where h is the Coxeter number. Thanks to the works of Kazhdan-Lusztig [Reference Kazhdan and LusztigKL93, Reference Kazhdan and LusztigKL94a, Reference Kazhdan and LusztigKL94b], Kashiwara-Tanisaki [Reference Kashiwara and TanisakiKT95, Reference Kashiwara and TanisakiKT96] and Andersen-Jantzen-Soergel [Reference Andersen, Jantzen and SoergelAJS94], this is proved for p large enough. An explicit bound on p is known by Fiebig [Reference FiebigFie12].
However, as Williamson [Reference WilliamsonWil17] showed, Lustzig’s conjecture fails for many p. Therefore, we need a new approach for such p. Riche-Williamson [Reference Riche and WilliamsonRW18] gave such an approach, and now we explain it. Assume that
![]() $p> h$
. Let
$p> h$
. Let
![]() $\operatorname {\mathrm {Rep}}_0(G)$
be the principal block of the category of rational representations of G. For each affine simple reflection s, we have the wall-crossing functor
$\operatorname {\mathrm {Rep}}_0(G)$
be the principal block of the category of rational representations of G. For each affine simple reflection s, we have the wall-crossing functor
![]() $\theta _s\colon \operatorname {\mathrm {Rep}}_0(G)\to \operatorname {\mathrm {Rep}}_0(G)$
. The Grothendieck group of
$\theta _s\colon \operatorname {\mathrm {Rep}}_0(G)\to \operatorname {\mathrm {Rep}}_0(G)$
. The Grothendieck group of
![]() $\operatorname {\mathrm {Rep}}_0(G)$
is isomorphic to the anti-spherical quotient of the group algebra of the affine Weyl group. Here, the action of the affine Weyl group on a representation is given by
$\operatorname {\mathrm {Rep}}_0(G)$
is isomorphic to the anti-spherical quotient of the group algebra of the affine Weyl group. Here, the action of the affine Weyl group on a representation is given by
![]() $[M](s + 1) = [\theta _s(M)]$
for
$[M](s + 1) = [\theta _s(M)]$
for
![]() $M\in \operatorname {\mathrm {Rep}}_0(G)$
and a simple affine reflection s. Riche-Williamson [Reference Riche and WilliamsonRW18] conjectured the existence of a categorification of this anti-spherical quotient. More precisely, they conjectured that there is an action of
$M\in \operatorname {\mathrm {Rep}}_0(G)$
and a simple affine reflection s. Riche-Williamson [Reference Riche and WilliamsonRW18] conjectured the existence of a categorification of this anti-spherical quotient. More precisely, they conjectured that there is an action of
![]() $\mathcal {D}$
on
$\mathcal {D}$
on
![]() $\operatorname {\mathrm {Rep}}_0(G)$
where
$\operatorname {\mathrm {Rep}}_0(G)$
where
![]() $\mathcal {D}$
is the diagrammatic Hecke category defined by Elias-Williamson [Reference Elias and WilliamsonEW16]. Assuming this conjecture, they proved that the anti-spherical quotient of
$\mathcal {D}$
is the diagrammatic Hecke category defined by Elias-Williamson [Reference Elias and WilliamsonEW16]. Assuming this conjecture, they proved that the anti-spherical quotient of
![]() $\mathcal {D}$
is a graded version of the category of tilting modules in
$\mathcal {D}$
is a graded version of the category of tilting modules in
![]() $\operatorname {\mathrm {Rep}}_0(G)$
. In particular, one can describe the character of indecomposable tilting modules in terms of p-Kazhdan-Lusztig polynomials. Recently this description was proved by Achar-Makisumi-Riche-Williamson [Reference Achar, Makisumi, Riche and WilliamsonAMRW19] when
$\operatorname {\mathrm {Rep}}_0(G)$
. In particular, one can describe the character of indecomposable tilting modules in terms of p-Kazhdan-Lusztig polynomials. Recently this description was proved by Achar-Makisumi-Riche-Williamson [Reference Achar, Makisumi, Riche and WilliamsonAMRW19] when
![]() $p> h$
, and for any p by Riche-Williamson [Reference Riche and WilliamsonRW22]. We note that if
$p> h$
, and for any p by Riche-Williamson [Reference Riche and WilliamsonRW22]. We note that if
![]() $p\ge 2h - 2$
, then characters for irreducible modules are described by characters of tilting modules [Reference Andersen, Carter and SaxlAnd98]. We also remark that Sobaje [Reference SobajeSob20] gave for all p an algorithm to calculate the characters of irreducible modules by the characters of indecomposable tilting modules.
$p\ge 2h - 2$
, then characters for irreducible modules are described by characters of tilting modules [Reference Andersen, Carter and SaxlAnd98]. We also remark that Sobaje [Reference SobajeSob20] gave for all p an algorithm to calculate the characters of irreducible modules by the characters of indecomposable tilting modules.
Achar-Makisumi-Riche-Williamson also proved a big part of the conjecture, but not a full statement. In the case of
![]() $G = \mathrm {GL}_n$
, the original conjecture is proved by Riche-Williamson [Reference Riche and WilliamsonRW18]. Recently, the conjecture is proved by Bezrukavnikov-Riche [Reference Bezrukavnikov and RicheBR22] for
$G = \mathrm {GL}_n$
, the original conjecture is proved by Riche-Williamson [Reference Riche and WilliamsonRW18]. Recently, the conjecture is proved by Bezrukavnikov-Riche [Reference Bezrukavnikov and RicheBR22] for
![]() $p> h$
.
$p> h$
.
In this paper, we consider the
![]() $G_1T$
-version of this conjecture, where
$G_1T$
-version of this conjecture, where
![]() $T\subset G$
is a maximal torus and
$T\subset G$
is a maximal torus and
![]() $G_1$
is the Frobenius kernel of G. Namely, we define an action of the category
$G_1$
is the Frobenius kernel of G. Namely, we define an action of the category
![]() $\mathcal {D}$
on the principal block of
$\mathcal {D}$
on the principal block of
![]() $G_1T$
-modules.
$G_1T$
-modules.
Next, we state our main theorem. We remark that we have an object
![]() $B_s\in \mathcal {D}$
for any affine simple reflection s (see the next subsection for the details). Assume that
$B_s\in \mathcal {D}$
for any affine simple reflection s (see the next subsection for the details). Assume that
![]() $p> h$
. Let
$p> h$
. Let
![]() $\operatorname {\mathrm {Rep}}_0(G_1T)$
be the principal block of the category of
$\operatorname {\mathrm {Rep}}_0(G_1T)$
be the principal block of the category of
![]() $G_1T$
-modules.
$G_1T$
-modules.
Theorem 1.1 (Theorem 3.31).
The category
![]() $\mathcal {D}$
acts on
$\mathcal {D}$
acts on
![]() $\operatorname {\mathrm {Rep}}_0(G_1T)$
, where
$\operatorname {\mathrm {Rep}}_0(G_1T)$
, where
![]() $B_s\in \mathcal {D}$
acts as the wall-crossing functor for any affine simple reflection s.
$B_s\in \mathcal {D}$
acts as the wall-crossing functor for any affine simple reflection s.
Kaneda (private communication) proved this theorem for
![]() $\mathrm {GL}_n$
using the arguments of Riche-Williamson [Reference Riche and WilliamsonRW18].
$\mathrm {GL}_n$
using the arguments of Riche-Williamson [Reference Riche and WilliamsonRW18].
Let
![]() $X^\vee $
be the cocharacter group of T and set
$X^\vee $
be the cocharacter group of T and set
![]() $X^\vee _{{\mathbb {K}}} = X^\vee \otimes _{{\mathbb {Z}}}{\mathbb {K}}$
. Let
$X^\vee _{{\mathbb {K}}} = X^\vee \otimes _{{\mathbb {Z}}}{\mathbb {K}}$
. Let
![]() $S = \operatorname {\mathrm {Sym}}(X^\vee _{{\mathbb {K}}})$
be the symmetric algebra of
$S = \operatorname {\mathrm {Sym}}(X^\vee _{{\mathbb {K}}})$
be the symmetric algebra of
![]() $X^\vee _{{\mathbb {K}}}$
. This is a graded algebra via
$X^\vee _{{\mathbb {K}}}$
. This is a graded algebra via
![]() $\deg (X^{\vee }_{{\mathbb {K}}}) = 2$
. Andersen-Jantzen-Soergel defined a combinatorial category
$\deg (X^{\vee }_{{\mathbb {K}}}) = 2$
. Andersen-Jantzen-Soergel defined a combinatorial category
![]() $\mathcal {K}_{{\mathrm {AJS}}}$
. This category is an S-linear category with a grading. We define a category
$\mathcal {K}_{{\mathrm {AJS}}}$
. This category is an S-linear category with a grading. We define a category
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}$
with the same objects as
${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}$
with the same objects as
![]() $\mathcal {K}_{{\mathrm {AJS}}}$
; however, the space of morphisms is defined as
$\mathcal {K}_{{\mathrm {AJS}}}$
; however, the space of morphisms is defined as
![]() $\operatorname {\mathrm {Hom}}_{{\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}}(M,N) = {\mathbb {K}}\otimes _{S}\bigoplus _{i\in {\mathbb {Z}}}\operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}}}}(M,N(i))$
, where
$\operatorname {\mathrm {Hom}}_{{\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}}(M,N) = {\mathbb {K}}\otimes _{S}\bigoplus _{i\in {\mathbb {Z}}}\operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}}}}(M,N(i))$
, where
![]() $N(i)$
denotes the grading shift (the upperscript
$N(i)$
denotes the grading shift (the upperscript
![]() $\mathrm {f}$
means forgetting the gradings). Let
$\mathrm {f}$
means forgetting the gradings). Let
![]() $\operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
be the category of projective objects in
$\operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
be the category of projective objects in
![]() $\operatorname {\mathrm {Rep}}_0(G_1T)$
. Andersen-Jantzen-Soergel constructed a functor
$\operatorname {\mathrm {Rep}}_0(G_1T)$
. Andersen-Jantzen-Soergel constructed a functor
![]() $\mathcal {V}\colon \operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))\to {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}$
and proved that it is fully faithful. They also determined the essential image of
$\mathcal {V}\colon \operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))\to {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}$
and proved that it is fully faithful. They also determined the essential image of
![]() $\mathcal {V}$
, and using this functor, they proved Lusztig’s conjecture for large p.
$\mathcal {V}$
, and using this functor, they proved Lusztig’s conjecture for large p.
In order to obtain an action of
![]() $\mathcal {D}$
on
$\mathcal {D}$
on
![]() $\operatorname {\mathrm {Rep}}_0(G_1T)$
, it is sufficient to define an action on
$\operatorname {\mathrm {Rep}}_0(G_1T)$
, it is sufficient to define an action on
![]() $\operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
(see 3.7). Therefore, by the results of Andersen-Jantzen-Soergel, it is sufficient to construct the action of
$\operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
(see 3.7). Therefore, by the results of Andersen-Jantzen-Soergel, it is sufficient to construct the action of
![]() $\mathcal {D}$
on the essential image of
$\mathcal {D}$
on the essential image of
![]() $\mathcal {V}$
. The main obstructions to do it are the following.
$\mathcal {V}$
. The main obstructions to do it are the following.
-
(1) Elias-Williamson defined
 $\mathcal {D}$
via generators and relations. Since the relations are very complicated, it is hard to check that the action is well-defined.
$\mathcal {D}$
via generators and relations. Since the relations are very complicated, it is hard to check that the action is well-defined. -
(2) The category
 $\mathcal {K}_{{\mathrm {AJS}},P}$
contains only “local” information. Hence, it is difficult to construct the action directly.
$\mathcal {K}_{{\mathrm {AJS}},P}$
contains only “local” information. Hence, it is difficult to construct the action directly.
1.1 The category
 ${\mathcal {S}\mathrm {Bimod}}$
${\mathcal {S}\mathrm {Bimod}}$
We use the category
![]() ${\mathcal {S}\mathrm {Bimod}}$
[Reference AbeAbe21] instead of the category
${\mathcal {S}\mathrm {Bimod}}$
[Reference AbeAbe21] instead of the category
![]() $\mathcal {D}$
. The category
$\mathcal {D}$
. The category
![]() ${\mathcal {S}\mathrm {Bimod}}$
is equivalent to the category
${\mathcal {S}\mathrm {Bimod}}$
is equivalent to the category
![]() $\mathcal {D}$
. We recall the definition of
$\mathcal {D}$
. We recall the definition of
![]() ${\mathcal {S}\mathrm {Bimod}}$
. Let
${\mathcal {S}\mathrm {Bimod}}$
. Let
![]() $W_{{\mathrm {aff}}}$
be the affine Weyl group attached to G and
$W_{{\mathrm {aff}}}$
be the affine Weyl group attached to G and
![]() $\operatorname {\mathrm {Frac}}(S)$
the field of fractions of S. An object M in
$\operatorname {\mathrm {Frac}}(S)$
the field of fractions of S. An object M in
![]() ${\mathcal {S}\mathrm {Bimod}}$
is a graded S-bimodule and submodules
${\mathcal {S}\mathrm {Bimod}}$
is a graded S-bimodule and submodules
![]() $M_{x}^{\operatorname {\mathrm {Frac}}(S)}\subset M\otimes _{S}\operatorname {\mathrm {Frac}}(S)\ (x\in W_{{\mathrm {aff}}})$
with the property
$M_{x}^{\operatorname {\mathrm {Frac}}(S)}\subset M\otimes _{S}\operatorname {\mathrm {Frac}}(S)\ (x\in W_{{\mathrm {aff}}})$
with the property
![]() $M\otimes _{S}\operatorname {\mathrm {Frac}}(S) = \bigoplus _{x\in W_{{\mathrm {aff}}}}M_x^{\operatorname {\mathrm {Frac}}(S)}$
and
$M\otimes _{S}\operatorname {\mathrm {Frac}}(S) = \bigoplus _{x\in W_{{\mathrm {aff}}}}M_x^{\operatorname {\mathrm {Frac}}(S)}$
and
![]() $mf = \overline {x}(f)m$
for
$mf = \overline {x}(f)m$
for
![]() $f\in S$
and
$f\in S$
and
![]() $m\in M_x^{\operatorname {\mathrm {Frac}}(S)}$
. Here,
$m\in M_x^{\operatorname {\mathrm {Frac}}(S)}$
. Here,
![]() $\overline {x}$
is the image of x in the finite Weyl group. For
$\overline {x}$
is the image of x in the finite Weyl group. For
![]() $M,N\in {\mathcal {S}\mathrm {Bimod}}$
, we have the tensor product
$M,N\in {\mathcal {S}\mathrm {Bimod}}$
, we have the tensor product
![]() $M\otimes N = M\otimes _{S}N$
with the decomposition
$M\otimes N = M\otimes _{S}N$
with the decomposition
![]() $(M\otimes N)\otimes _{S}\operatorname {\mathrm {Frac}}(S) = \bigoplus _{x\in W_{{\mathrm {aff}}}} (M\otimes N)_x^{\operatorname {\mathrm {Frac}}(S)}$
, where
$(M\otimes N)\otimes _{S}\operatorname {\mathrm {Frac}}(S) = \bigoplus _{x\in W_{{\mathrm {aff}}}} (M\otimes N)_x^{\operatorname {\mathrm {Frac}}(S)}$
, where
![]() $(M\otimes N)_x^{\operatorname {\mathrm {Frac}}(S)} = \bigoplus _{yz = x}M_{y}^{\operatorname {\mathrm {Frac}}(S)}\otimes _{\operatorname {\mathrm {Frac}}(S)} N_{z}^{\operatorname {\mathrm {Frac}}(S)}$
. A homomorphism
$(M\otimes N)_x^{\operatorname {\mathrm {Frac}}(S)} = \bigoplus _{yz = x}M_{y}^{\operatorname {\mathrm {Frac}}(S)}\otimes _{\operatorname {\mathrm {Frac}}(S)} N_{z}^{\operatorname {\mathrm {Frac}}(S)}$
. A homomorphism
![]() $M\to N$
is a degree zero S-bimodule homomorphism which sends
$M\to N$
is a degree zero S-bimodule homomorphism which sends
![]() $M_x^{\operatorname {\mathrm {Frac}}(S)}$
to
$M_x^{\operatorname {\mathrm {Frac}}(S)}$
to
![]() $N_x^{\operatorname {\mathrm {Frac}}(S)}$
for any
$N_x^{\operatorname {\mathrm {Frac}}(S)}$
for any
![]() $x\in W_{{\mathrm {aff}}}$
.
$x\in W_{{\mathrm {aff}}}$
.
Let X be the character group of T. An alcove is a connected component of
![]() $X\otimes _{{\mathbb {Z}}}{\mathbb {R}}\setminus \bigcup _t H_t$
, where t runs through the affine reflections in
$X\otimes _{{\mathbb {Z}}}{\mathbb {R}}\setminus \bigcup _t H_t$
, where t runs through the affine reflections in
![]() $W_{{\mathrm {aff}}}$
, and
$W_{{\mathrm {aff}}}$
, and
![]() $H_t$
is the fixed hyperplane of t. We fix an alcove
$H_t$
is the fixed hyperplane of t. We fix an alcove
![]() $A_0$
and let
$A_0$
and let
![]() $S_{{\mathrm {aff}}}$
be the reflections with respect to the walls of
$S_{{\mathrm {aff}}}$
be the reflections with respect to the walls of
![]() $A_0$
. Then,
$A_0$
. Then,
![]() $(W_{{\mathrm {aff}}},S_{{\mathrm {aff}}})$
is a Coxeter system. For each
$(W_{{\mathrm {aff}}},S_{{\mathrm {aff}}})$
is a Coxeter system. For each
![]() $s\in S_{{\mathrm {aff}}}$
, put
$s\in S_{{\mathrm {aff}}}$
, put
![]() $S^s = \{f\in S\mid s(f) = f\}$
. Then, the S-bimodule
$S^s = \{f\in S\mid s(f) = f\}$
. Then, the S-bimodule
![]() $S\otimes _{S^s}S(1)$
has, when tensored by
$S\otimes _{S^s}S(1)$
has, when tensored by
![]() $\operatorname {\mathrm {Frac}}(S)$
, a unique decomposition as described above such that
$\operatorname {\mathrm {Frac}}(S)$
, a unique decomposition as described above such that
![]() $(S\otimes _{S^s}S(1))_w^{\operatorname {\mathrm {Frac}}(S)}\ne 0$
only when
$(S\otimes _{S^s}S(1))_w^{\operatorname {\mathrm {Frac}}(S)}\ne 0$
only when
![]() $w = e,s$
. Let
$w = e,s$
. Let
![]() $B_{s}$
be this object. Now
$B_{s}$
be this object. Now
![]() ${\mathcal {S}\mathrm {Bimod}}$
consists of the objects M which are direct summands of direct sums of objects of the form
${\mathcal {S}\mathrm {Bimod}}$
consists of the objects M which are direct summands of direct sums of objects of the form
![]() $B_{s_1}\otimes \dotsm \otimes B_{s_l}(n)$
where
$B_{s_1}\otimes \dotsm \otimes B_{s_l}(n)$
where
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
and
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
and
![]() $n\in {\mathbb {Z}}$
. It is proved in [Reference AbeAbe21] that the category
$n\in {\mathbb {Z}}$
. It is proved in [Reference AbeAbe21] that the category
![]() ${\mathcal {S}\mathrm {Bimod}}$
is equivalent to the diagrammatic Hecke category defined by Elias-Williamson. As shown in [Reference Elias and WilliamsonEW16, Reference AbeAbe21], this gives a categorification of the Hecke algebra of the affine Weyl group; namely, the split Grothendieck group of
${\mathcal {S}\mathrm {Bimod}}$
is equivalent to the diagrammatic Hecke category defined by Elias-Williamson. As shown in [Reference Elias and WilliamsonEW16, Reference AbeAbe21], this gives a categorification of the Hecke algebra of the affine Weyl group; namely, the split Grothendieck group of
![]() ${\mathcal {S}\mathrm {Bimod}}$
is isomorphic to the Hecke algebra.
${\mathcal {S}\mathrm {Bimod}}$
is isomorphic to the Hecke algebra.
1.2 Another combinatorial category
We also give another realization of the category of Andersen-Jantzen-Soergel
![]() $\mathcal {K}_{{\mathrm {AJS}}}$
[Reference Andersen, Jantzen and SoergelAJS94]. As in [Reference LusztigLus80], we use the combinatorics of alcoves to define the category. Let
$\mathcal {K}_{{\mathrm {AJS}}}$
[Reference Andersen, Jantzen and SoergelAJS94]. As in [Reference LusztigLus80], we use the combinatorics of alcoves to define the category. Let
![]() $\mathcal {A}$
be the set of alcoves. We fix a positive system
$\mathcal {A}$
be the set of alcoves. We fix a positive system
![]() $\Delta ^+$
of the root system
$\Delta ^+$
of the root system
![]() $\Delta $
of G. Then, this defines an order on
$\Delta $
of G. Then, this defines an order on
![]() $\mathcal {A}$
[Reference LusztigLus80]. Recall that we have fixed
$\mathcal {A}$
[Reference LusztigLus80]. Recall that we have fixed
![]() $A_0\in \mathcal {A}$
. The action of
$A_0\in \mathcal {A}$
. The action of
![]() $W_{{\mathrm {aff}}}$
on
$W_{{\mathrm {aff}}}$
on
![]() $X\otimes _{{\mathbb {Z}}}{\mathbb {R}}$
induces the action of
$X\otimes _{{\mathbb {Z}}}{\mathbb {R}}$
induces the action of
![]() $W_{{\mathrm {aff}}}$
on
$W_{{\mathrm {aff}}}$
on
![]() $\mathcal {A}$
such that the map
$\mathcal {A}$
such that the map
![]() $w\mapsto w(A_0)$
gives a bijection
$w\mapsto w(A_0)$
gives a bijection
![]() $W_{{\mathrm {aff}}}\to \mathcal {A}$
.
$W_{{\mathrm {aff}}}\to \mathcal {A}$
.
Set
![]() $S^{\emptyset } = S[(\alpha ^\vee )^{-1}\mid \alpha \in \Delta ]$
. We define the category
$S^{\emptyset } = S[(\alpha ^\vee )^{-1}\mid \alpha \in \Delta ]$
. We define the category
![]() $\widetilde {\mathcal {K}}'$
as follows. An object of
$\widetilde {\mathcal {K}}'$
as follows. An object of
![]() $\widetilde {\mathcal {K}}'$
is a graded S-bimodule M with a decomposition
$\widetilde {\mathcal {K}}'$
is a graded S-bimodule M with a decomposition
![]() $S^\emptyset \otimes _{S}M = \bigoplus _{A\in \mathcal {A}}M_A^{\emptyset }$
, such that
$S^\emptyset \otimes _{S}M = \bigoplus _{A\in \mathcal {A}}M_A^{\emptyset }$
, such that
![]() $mf = \overline {x}(f)m$
for
$mf = \overline {x}(f)m$
for
![]() $m\in M_{A}^{\emptyset }$
,
$m\in M_{A}^{\emptyset }$
,
![]() $f\in S^{\emptyset }$
,
$f\in S^{\emptyset }$
,
![]() $x\in W_{{\mathrm {aff}}}$
such that
$x\in W_{{\mathrm {aff}}}$
such that
![]() $A = x(A_0)$
and
$A = x(A_0)$
and
![]() $\overline {x}$
is the image of x in the finite Weyl group. A morphism
$\overline {x}$
is the image of x in the finite Weyl group. A morphism
![]() $f\colon M\to N$
is a degree zero S-bimodule homomorphism, such that
$f\colon M\to N$
is a degree zero S-bimodule homomorphism, such that
![]() $f(M_A^{\emptyset })\subset \bigoplus _{A' \ge A}N_{A'}^{\emptyset }$
. We will also define some subcategories of
$f(M_A^{\emptyset })\subset \bigoplus _{A' \ge A}N_{A'}^{\emptyset }$
. We will also define some subcategories of
![]() $\widetilde {\mathcal {K}}'$
. Particularly, the category denoted by
$\widetilde {\mathcal {K}}'$
. Particularly, the category denoted by
![]() $\widetilde {\mathcal {K}}_P$
plays an important role in our construction. Since it is technical, we do not say anything about its definitions in the Introduction, but instead refer to Definition 2.16. We only note that, for each
$\widetilde {\mathcal {K}}_P$
plays an important role in our construction. Since it is technical, we do not say anything about its definitions in the Introduction, but instead refer to Definition 2.16. We only note that, for each
![]() $A\in \mathcal {A}$
, the module
$A\in \mathcal {A}$
, the module
![]() $M_{\{A\}} = (M\cap \bigoplus _{A'\ge A}M_{A'}^{\emptyset })/(M\cap \bigoplus _{A'> A}M_{A'}^{\emptyset })$
is graded free for
$M_{\{A\}} = (M\cap \bigoplus _{A'\ge A}M_{A'}^{\emptyset })/(M\cap \bigoplus _{A'> A}M_{A'}^{\emptyset })$
is graded free for
![]() $M\in \widetilde {\mathcal {K}}_P$
.
$M\in \widetilde {\mathcal {K}}_P$
.
We define an action
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\widetilde {\mathcal {K}}'$
as follows. Let
$\widetilde {\mathcal {K}}'$
as follows. Let
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
and note that we have a submodule
$B\in {\mathcal {S}\mathrm {Bimod}}$
and note that we have a submodule
![]() $B^{\emptyset }_{x}\subset B\otimes _{S}S^{\emptyset }$
, such that
$B^{\emptyset }_{x}\subset B\otimes _{S}S^{\emptyset }$
, such that
![]() $B^{\emptyset }_x\otimes _{S^{\emptyset }}\operatorname {\mathrm {Frac}}(S) = B_x^{\operatorname {\mathrm {Frac}}(S)}$
. Let
$B^{\emptyset }_x\otimes _{S^{\emptyset }}\operatorname {\mathrm {Frac}}(S) = B_x^{\operatorname {\mathrm {Frac}}(S)}$
. Let
![]() $M\in \widetilde {\mathcal {K}}'$
. Then, we define
$M\in \widetilde {\mathcal {K}}'$
. Then, we define
![]() $M*B$
by
$M*B$
by
![]() $M*B = M\otimes _{S}B$
as a graded S-bimodule and
$M*B = M\otimes _{S}B$
as a graded S-bimodule and
![]() $(M*B)_{w(A_0)}^{\emptyset } = \bigoplus _{x\in W_{{\mathrm {aff}}}}M_{wx^{-1}(A_0)}^{\emptyset }\otimes _{S^{\emptyset }}B_{x}^{\emptyset }$
for
$(M*B)_{w(A_0)}^{\emptyset } = \bigoplus _{x\in W_{{\mathrm {aff}}}}M_{wx^{-1}(A_0)}^{\emptyset }\otimes _{S^{\emptyset }}B_{x}^{\emptyset }$
for
![]() $w\in W_{{\mathrm {aff}}}$
. We can prove that the above action of
$w\in W_{{\mathrm {aff}}}$
. We can prove that the above action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\widetilde {\mathcal {K}}'$
induces a well-defined action also on
$\widetilde {\mathcal {K}}'$
induces a well-defined action also on
![]() $\widetilde {\mathcal {K}}_{P}$
(Proposition 2.24). Therefore, the split Grothendieck group
$\widetilde {\mathcal {K}}_{P}$
(Proposition 2.24). Therefore, the split Grothendieck group
![]() $[\widetilde {\mathcal {K}}_{P}]$
of
$[\widetilde {\mathcal {K}}_{P}]$
of
![]() $\widetilde {\mathcal {K}}_{P}$
has a structure of
$\widetilde {\mathcal {K}}_{P}$
has a structure of
![]() $[{\mathcal {S}\mathrm {Bimod}}]$
-module defined by
$[{\mathcal {S}\mathrm {Bimod}}]$
-module defined by
![]() $[M][B] = [M*B]$
. Hence,
$[M][B] = [M*B]$
. Hence,
![]() $[\widetilde {\mathcal {K}}_{P}]$
is a module of the Hecke algebra. This category satisfies the following.
$[\widetilde {\mathcal {K}}_{P}]$
is a module of the Hecke algebra. This category satisfies the following.
Theorem 1.2 (Theorem 2.35, 2.40).
We have the following.
-
(1) For each
 $A\in \mathcal {A}$
, we have an indecomposable module
$A\in \mathcal {A}$
, we have an indecomposable module
 $Q(A)\in \widetilde {\mathcal {K}}_{P}$
, such that
$Q(A)\in \widetilde {\mathcal {K}}_{P}$
, such that
 $Q(A)_{\{A\}}\simeq S$
and
$Q(A)_{\{A\}}\simeq S$
and
 $Q(A)_{\{A'\}}\ne 0$
implies
$Q(A)_{\{A'\}}\ne 0$
implies
 $A'\ge A$
.
$A'\ge A$
. -
(2) Any object in
 $\widetilde {\mathcal {K}}_{P}$
is isomorphic to a direct sum of
$\widetilde {\mathcal {K}}_{P}$
is isomorphic to a direct sum of
 $Q(A)(n)$
for
$Q(A)(n)$
for
 $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
 $n\in {\mathbb {Z}}$
.
$n\in {\mathbb {Z}}$
. -
(3) The split Grothendieck group
 $[\widetilde {\mathcal {K}}_P]$
is isomorphic to a certain submodule
$[\widetilde {\mathcal {K}}_P]$
is isomorphic to a certain submodule
 $\mathcal {P}^0$
of the periodic Hecke module (the submodule was introduced in [Reference LusztigLus80]).
$\mathcal {P}^0$
of the periodic Hecke module (the submodule was introduced in [Reference LusztigLus80]).
1.3 A relation with a work of Fiebig-Lanini
Fiebig-Lanini [Reference Fiebig and LaniniFL15] had a similar work (earlier than this work) and defined a certain category. Logically, results in this paper do not depend on their work. However, in the proofs in this paper, we borrow many ideas from their work. Moreover, in subsection 2.9, we prove that our category
![]() $\widetilde {\mathcal {K}}_P$
is equivalent to the category of Fiebig-Lanini. The author thinks it is possible to establish the theory on top of the theory of Fiebig-Lanini, but the existence of a Hecke action does not easily follow from their theory.
$\widetilde {\mathcal {K}}_P$
is equivalent to the category of Fiebig-Lanini. The author thinks it is possible to establish the theory on top of the theory of Fiebig-Lanini, but the existence of a Hecke action does not easily follow from their theory.
1.4 Relations with representation theory
The category
![]() $\widetilde {\mathcal {K}}_{P}$
is not the category we really need. We modify this category as follows. Objects in
$\widetilde {\mathcal {K}}_{P}$
is not the category we really need. We modify this category as follows. Objects in
![]() $\mathcal {K}_{P}$
are the same as those in
$\mathcal {K}_{P}$
are the same as those in
![]() $\widetilde {\mathcal {K}}_{P}$
, and the space of homomorphisms is defined by
$\widetilde {\mathcal {K}}_{P}$
, and the space of homomorphisms is defined by
We prove that the action of
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
on
$B\in {\mathcal {S}\mathrm {Bimod}}$
on
![]() $\mathcal {K}_{P}$
is well-defined.
$\mathcal {K}_{P}$
is well-defined.
Theorem 1.3 (Proposition 3.3, Theorem 3.9).
We have the following.
-
(1) The object
 $Q(A)$
is also indecomposable as an object of
$Q(A)$
is also indecomposable as an object of
 $\mathcal {K}_{P}$
.
$\mathcal {K}_{P}$
. -
(2) We have
 $[\mathcal {K}_{P}]\simeq [\widetilde {\mathcal {K}}_P]$
. Hence
$[\mathcal {K}_{P}]\simeq [\widetilde {\mathcal {K}}_P]$
. Hence
 $[\mathcal {K}_{P}]$
is also isomorphic to
$[\mathcal {K}_{P}]$
is also isomorphic to
 $\mathcal {P}^0$
.
$\mathcal {P}^0$
.
We also define a functor
![]() $\mathcal {F}\colon \mathcal {K}_{P}\to \mathcal {K}_{{\mathrm {AJS}}}$
. Recall that we have a wall-crossing functor
$\mathcal {F}\colon \mathcal {K}_{P}\to \mathcal {K}_{{\mathrm {AJS}}}$
. Recall that we have a wall-crossing functor
![]() $\vartheta _s\colon \mathcal {K}_{{\mathrm {AJS}}}\to \mathcal {K}_{{\mathrm {AJS}}}$
for each
$\vartheta _s\colon \mathcal {K}_{{\mathrm {AJS}}}\to \mathcal {K}_{{\mathrm {AJS}}}$
for each
![]() $s\in S_{{\mathrm {aff}}}$
, see [Reference FiebigFie11, 5.3].
$s\in S_{{\mathrm {aff}}}$
, see [Reference FiebigFie11, 5.3].
Theorem 1.4 (Proposition 3.14, 3.26).
Let
![]() $M\in \mathcal {K}_{P}$
. We have the following.
$M\in \mathcal {K}_{P}$
. We have the following.
-
(1) We have
 $\mathcal {F}(M*B_s)\simeq \vartheta _s(\mathcal {F}(M))$
for each
$\mathcal {F}(M*B_s)\simeq \vartheta _s(\mathcal {F}(M))$
for each
 $s\in S_{{\mathrm {aff}}}$
.
$s\in S_{{\mathrm {aff}}}$
. -
(2) The functor
 $\mathcal {F}$
is fully faithful.
$\mathcal {F}$
is fully faithful.
Let
![]() $\mathcal {K}_{{\mathrm {AJS}},P}$
be the essential image of
$\mathcal {K}_{{\mathrm {AJS}},P}$
be the essential image of
![]() $\mathcal {F}$
. We define
$\mathcal {F}$
. We define
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}},P}$
and
${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}},P}$
and
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{P}$
in the same way as
${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{P}$
in the same way as
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}}}$
. One of the main results in [Reference Andersen, Jantzen and SoergelAJS94] says that
${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}}}$
. One of the main results in [Reference Andersen, Jantzen and SoergelAJS94] says that
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}},P}\simeq \operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
(see 3.7). Since the action of
${\mathbb {K}}\otimes _{S}\mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}},P}\simeq \operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
(see 3.7). Since the action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\mathcal {K}_P\simeq \mathcal {K}_{{\mathrm {AJS}},P}$
gives an action on
$\mathcal {K}_P\simeq \mathcal {K}_{{\mathrm {AJS}},P}$
gives an action on
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}$
, we now get the action of
${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}$
, we now get the action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
. We can extend this action to
$\operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
. We can extend this action to
![]() $\operatorname {\mathrm {Rep}}_0(G_1T)$
(see 3.7).
$\operatorname {\mathrm {Rep}}_0(G_1T)$
(see 3.7).
Let
![]() $A_0$
be the alcove containing
$A_0$
be the alcove containing
![]() $\rho /p$
where
$\rho /p$
where
![]() $\rho $
is the half sum of positive roots. We have an equivalence
$\rho $
is the half sum of positive roots. We have an equivalence
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}^{\mathrm {f}}\simeq {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}\simeq \operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
and
${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}^{\mathrm {f}}\simeq {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}\simeq \operatorname {\mathrm {Proj}}(\operatorname {\mathrm {Rep}}_0(G_1T))$
and
![]() $Q(A)$
corresponds to
$Q(A)$
corresponds to
![]() $P(\lambda _A)$
, where
$P(\lambda _A)$
, where
![]() $\lambda _{w(A_0)} = pw(\rho /p) - \rho $
for
$\lambda _{w(A_0)} = pw(\rho /p) - \rho $
for
![]() $w\in W_{{\mathrm {aff}}}$
and
$w\in W_{{\mathrm {aff}}}$
and
![]() $P(\lambda _A)$
is the projective cover of the irreducible representation with highest weight
$P(\lambda _A)$
is the projective cover of the irreducible representation with highest weight
![]() $\lambda _A$
. Let
$\lambda _A$
. Let
![]() $Z(\mu )\in \operatorname {\mathrm {Rep}}(G_1T)$
be the baby Verma module with highest weight
$Z(\mu )\in \operatorname {\mathrm {Rep}}(G_1T)$
be the baby Verma module with highest weight
![]() $\mu $
and
$\mu $
and
![]() $(P(\lambda ):Z(\mu ))$
the multiplicity of
$(P(\lambda ):Z(\mu ))$
the multiplicity of
![]() $Z(\mu )$
in a Verma flag of
$Z(\mu )$
in a Verma flag of
![]() $P(\lambda )$
. By the constructions, we have the following.
$P(\lambda )$
. By the constructions, we have the following.
Theorem 1.5 (Corollary 3.36).
The multiplicity
![]() $(P(\lambda _A):Z(\lambda _{A'}))$
is equal to the rank of
$(P(\lambda _A):Z(\lambda _{A'}))$
is equal to the rank of
![]() $Q(A)_{\{A'\}}$
.
$Q(A)_{\{A'\}}$
.
In 3.9, we discuss Lusztig’s conjecture on irreducible characters of rational representations. We give a proof of the conjecture based on the theory developed in this paper.
2 Our combinatorial category
We shall use a different notation than the Introduction. In particular, we do not fix the alcove
![]() $A_0$
. So, we distinguish two actions (from the right and left) of
$A_0$
. So, we distinguish two actions (from the right and left) of
![]() $W_{{\mathrm {aff}}}$
on
$W_{{\mathrm {aff}}}$
on
![]() $\mathcal {A}$
as in [Reference LusztigLus80]. We will also work in a more general situation than in the Introduction. Forget every notation and the assumptions from the Introduction. Notation used in the main body of this paper will be explained.
$\mathcal {A}$
as in [Reference LusztigLus80]. We will also work in a more general situation than in the Introduction. Forget every notation and the assumptions from the Introduction. Notation used in the main body of this paper will be explained.
2.1 Notation
Let
![]() $(X,\Delta ,X^\vee ,\Delta ^\vee )$
be a root datum. Let
$(X,\Delta ,X^\vee ,\Delta ^\vee )$
be a root datum. Let
![]() $\mathcal {A}$
the set of alcoves, namely the set of connected components of
$\mathcal {A}$
the set of alcoves, namely the set of connected components of
![]() $X_{\mathbb {R}}\setminus \bigcup _{\alpha \in \Delta ,n\in {\mathbb {Z}}}\{\lambda \in X_{\mathbb {R}}\mid \langle \lambda ,\alpha ^\vee \rangle = n\}$
where
$X_{\mathbb {R}}\setminus \bigcup _{\alpha \in \Delta ,n\in {\mathbb {Z}}}\{\lambda \in X_{\mathbb {R}}\mid \langle \lambda ,\alpha ^\vee \rangle = n\}$
where
![]() $X_{{\mathbb {R}}} = X\otimes _{{\mathbb {Z}}}{\mathbb {R}}$
. Let
$X_{{\mathbb {R}}} = X\otimes _{{\mathbb {Z}}}{\mathbb {R}}$
. Let
![]() $W_{\mathrm {f}}$
be the finite Weyl group and
$W_{\mathrm {f}}$
be the finite Weyl group and
![]() $W^{\prime }_{\mathrm {aff}} = W_{\mathrm {f}}\ltimes {\mathbb {Z}}\Delta $
the affine Weyl group with the natural surjective homomorphism
$W^{\prime }_{\mathrm {aff}} = W_{\mathrm {f}}\ltimes {\mathbb {Z}}\Delta $
the affine Weyl group with the natural surjective homomorphism
![]() $W^{\prime }_{\mathrm {aff}}\to W_{\mathrm {f}}$
. For each
$W^{\prime }_{\mathrm {aff}}\to W_{\mathrm {f}}$
. For each
![]() $\alpha \in \Delta $
and
$\alpha \in \Delta $
and
![]() $n\in {\mathbb {Z}}$
, let
$n\in {\mathbb {Z}}$
, let
![]() $s_{\alpha ,n}\colon X\to X$
be the reflection with respect to
$s_{\alpha ,n}\colon X\to X$
be the reflection with respect to
![]() $\{\lambda \in X_{\mathbb {R}}\mid \langle \lambda ,\alpha ^\vee \rangle = n\}$
. As in [Reference LusztigLus80], let
$\{\lambda \in X_{\mathbb {R}}\mid \langle \lambda ,\alpha ^\vee \rangle = n\}$
. As in [Reference LusztigLus80], let
![]() $S_{\mathrm {aff}}$
be the set of
$S_{\mathrm {aff}}$
be the set of
![]() $W^{\prime }_{\mathrm {aff}}$
-orbits on the set of faces. Then, for each
$W^{\prime }_{\mathrm {aff}}$
-orbits on the set of faces. Then, for each
![]() $s\in S_{\mathrm {aff}}$
and
$s\in S_{\mathrm {aff}}$
and
![]() $A\in \mathcal {A}$
, we denote
$A\in \mathcal {A}$
, we denote
![]() $As$
as the alcove
$As$
as the alcove
![]() $\ne A$
, which has a common face of type s with A. The subgroup of
$\ne A$
, which has a common face of type s with A. The subgroup of
![]() $\operatorname {\mathrm {Aut}}(\mathcal {A})$
(permutations of elements in
$\operatorname {\mathrm {Aut}}(\mathcal {A})$
(permutations of elements in
![]() $\mathcal {A}$
) generated by
$\mathcal {A}$
) generated by
![]() $S_{\mathrm {aff}}$
is denoted by
$S_{\mathrm {aff}}$
is denoted by
![]() $W_{\mathrm {aff}}$
. Then,
$W_{\mathrm {aff}}$
. Then,
![]() $(W_{\mathrm {aff}},S_{\mathrm {aff}})$
is a Coxeter system isomorphic to the affine Weyl group. The Bruhat order on
$(W_{\mathrm {aff}},S_{\mathrm {aff}})$
is a Coxeter system isomorphic to the affine Weyl group. The Bruhat order on
![]() $W_{{\mathrm {aff}}}$
is denoted by
$W_{{\mathrm {aff}}}$
is denoted by
![]() $\ge $
. We shall consider the right action of
$\ge $
. We shall consider the right action of
![]() $W_{{\mathrm {aff}}}$
on
$W_{{\mathrm {aff}}}$
on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
We give related notation and also some facts. If we fix an alcove
![]() $A_0$
, then
$A_0$
, then
![]() $W^{\prime }_{\mathrm {aff}}\simeq \mathcal {A}$
via
$W^{\prime }_{\mathrm {aff}}\simeq \mathcal {A}$
via
![]() $w\mapsto wA_0$
and
$w\mapsto wA_0$
and
![]() $W^{\prime }_{\mathrm {aff}}$
acts on
$W^{\prime }_{\mathrm {aff}}$
acts on
![]() $\mathcal {A}$
by
$\mathcal {A}$
by
![]() $(w(A_0))x = wx(A_0)$
. This gives an isomorphism
$(w(A_0))x = wx(A_0)$
. This gives an isomorphism
![]() $W^{\prime }_{\mathrm {aff}}\simeq W_{\mathrm {aff}}$
. The facts stated below are obvious from this description.
$W^{\prime }_{\mathrm {aff}}\simeq W_{\mathrm {aff}}$
. The facts stated below are obvious from this description.
Let
![]() $\Lambda $
be the set of maps
$\Lambda $
be the set of maps
![]() $\lambda \colon \mathcal {A}\to X$
such that
$\lambda \colon \mathcal {A}\to X$
such that
![]() $\lambda (xA) = \overline {x}\lambda (A)$
for any
$\lambda (xA) = \overline {x}\lambda (A)$
for any
![]() $x\in W^{\prime }_{\mathrm {aff}}$
and
$x\in W^{\prime }_{\mathrm {aff}}$
and
![]() $A\in \mathcal {A}$
, where
$A\in \mathcal {A}$
, where
![]() $\overline {x}\in W_{\mathrm {f}}$
is the image of x. We write
$\overline {x}\in W_{\mathrm {f}}$
is the image of x. We write
![]() $\lambda _A = \lambda (A)$
for
$\lambda _A = \lambda (A)$
for
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $A\in \mathcal {A}$
. For each
$A\in \mathcal {A}$
. For each
![]() $A\in \mathcal {A}$
,
$A\in \mathcal {A}$
,
![]() $\lambda \mapsto \lambda _A$
gives an isomorphism
$\lambda \mapsto \lambda _A$
gives an isomorphism
![]() $\Lambda \xrightarrow {\sim }X$
, and the inverse of this isomorphism is denoted by
$\Lambda \xrightarrow {\sim }X$
, and the inverse of this isomorphism is denoted by
![]() $\nu \mapsto \nu ^A$
. The group
$\nu \mapsto \nu ^A$
. The group
![]() $W_{\mathrm {aff}}$
acts on
$W_{\mathrm {aff}}$
acts on
![]() $\Lambda $
by
$\Lambda $
by
![]() $(x(\lambda ))(A) = \lambda (Ax)$
.
$(x(\lambda ))(A) = \lambda (Ax)$
.
Let
![]() $\Lambda _{\mathrm {aff}}$
be the set of
$\Lambda _{\mathrm {aff}}$
be the set of
![]() $\lambda \in \Lambda $
such that
$\lambda \in \Lambda $
such that
![]() $\lambda _A\in {\mathbb {Z}}\Delta $
for any, or equivalently, some
$\lambda _A\in {\mathbb {Z}}\Delta $
for any, or equivalently, some
![]() $A\in \mathcal {A}$
. For
$A\in \mathcal {A}$
. For
![]() $\lambda \in \Lambda _{\mathrm {aff}}$
and
$\lambda \in \Lambda _{\mathrm {aff}}$
and
![]() $A\in \mathcal {A}$
, we define
$A\in \mathcal {A}$
, we define
![]() $A\lambda = A + \lambda _A$
. Then, for
$A\lambda = A + \lambda _A$
. Then, for
![]() $\lambda _1,\lambda _2\in \Lambda _{\mathrm {aff}}$
,
$\lambda _1,\lambda _2\in \Lambda _{\mathrm {aff}}$
,
![]() $(A\lambda _1)\lambda _2 = (A + (\lambda _1)_A)\lambda _2 = A + (\lambda _1)_A + (\lambda _2)_{A + (\lambda _1)_A}$
. Since elements in
$(A\lambda _1)\lambda _2 = (A + (\lambda _1)_A)\lambda _2 = A + (\lambda _1)_A + (\lambda _2)_{A + (\lambda _1)_A}$
. Since elements in
![]() $\Lambda $
are constant on
$\Lambda $
are constant on
![]() ${\mathbb {Z}}\Delta $
-orbits, we have
${\mathbb {Z}}\Delta $
-orbits, we have
![]() $(\lambda _2)_{A + (\lambda _1)_A} = (\lambda _2)_A$
. Hence,
$(\lambda _2)_{A + (\lambda _1)_A} = (\lambda _2)_A$
. Hence,
![]() $(A\lambda _1)\lambda _2 = A + (\lambda _1 + \lambda _2)_A$
; namely,
$(A\lambda _1)\lambda _2 = A + (\lambda _1 + \lambda _2)_A$
; namely,
![]() $(A,\lambda )\mapsto A\lambda $
gives an action of
$(A,\lambda )\mapsto A\lambda $
gives an action of
![]() $\Lambda _{\mathrm {aff}}$
on
$\Lambda _{\mathrm {aff}}$
on
![]() $\mathcal {A}$
. Therefore, we get
$\mathcal {A}$
. Therefore, we get
![]() $\Lambda _{\mathrm {aff}}\hookrightarrow \operatorname {\mathrm {Aut}}(\mathcal {A})$
and the image is contained in
$\Lambda _{\mathrm {aff}}\hookrightarrow \operatorname {\mathrm {Aut}}(\mathcal {A})$
and the image is contained in
![]() $W_{\mathrm {aff}}$
. Thus, we may regard
$W_{\mathrm {aff}}$
. Thus, we may regard
![]() $\Lambda _{{\mathrm {aff}}}$
as a subgroup of
$\Lambda _{{\mathrm {aff}}}$
as a subgroup of
![]() $W_{{\mathrm {aff}}}$
.
$W_{{\mathrm {aff}}}$
.
Let
![]() $\lambda \in \Lambda $
and
$\lambda \in \Lambda $
and
![]() $A,A'\in \mathcal {A}$
and assume that
$A,A'\in \mathcal {A}$
and assume that
![]() $A,A'$
are in the same
$A,A'$
are in the same
![]() $\Lambda _{\mathrm {aff}}$
-orbit. Namely, there exists
$\Lambda _{\mathrm {aff}}$
-orbit. Namely, there exists
![]() $\mu \in \Lambda _{\mathrm {aff}}$
such that
$\mu \in \Lambda _{\mathrm {aff}}$
such that
![]() $A = A' \mu = A' + \mu _{A'}$
. Since elements in
$A = A' \mu = A' + \mu _{A'}$
. Since elements in
![]() $\Lambda $
are constant on
$\Lambda $
are constant on
![]() ${\mathbb {Z}}\Delta $
-orbits, we get
${\mathbb {Z}}\Delta $
-orbits, we get
![]() $\lambda _{A'} = \lambda _A$
. Namely, the isomorphism
$\lambda _{A'} = \lambda _A$
. Namely, the isomorphism
![]() $\lambda \mapsto \lambda _A$
only depends on
$\lambda \mapsto \lambda _A$
only depends on
![]() $\Lambda _{{\mathrm {aff}}}$
-orbit in
$\Lambda _{{\mathrm {aff}}}$
-orbit in
![]() $\mathcal {A}$
. Hence, we also write the isomorphism by
$\mathcal {A}$
. Hence, we also write the isomorphism by
![]() $\lambda \mapsto \lambda _\Omega $
where
$\lambda \mapsto \lambda _\Omega $
where
![]() $\Omega \in \mathcal {A}/\Lambda _{\mathrm {aff}}$
. The inverse is denoted by
$\Omega \in \mathcal {A}/\Lambda _{\mathrm {aff}}$
. The inverse is denoted by
![]() $\lambda \mapsto \lambda ^\Omega $
. The
$\lambda \mapsto \lambda ^\Omega $
. The
![]() $\Lambda _{\mathrm {aff}}$
-orbit through A is equal to
$\Lambda _{\mathrm {aff}}$
-orbit through A is equal to
![]() $\{A + \lambda \mid \lambda \in {\mathbb {Z}}\Delta \}$
. Let
$\{A + \lambda \mid \lambda \in {\mathbb {Z}}\Delta \}$
. Let
![]() $A + {\mathbb {Z}}\Delta $
be this set.
$A + {\mathbb {Z}}\Delta $
be this set.
The following lemma is obvious from the definitions.
Lemma 2.1. Let
![]() $\lambda \in \Lambda $
,
$\lambda \in \Lambda $
,
![]() $\nu \in X$
,
$\nu \in X$
,
![]() $x\in W_{\mathrm {aff}}$
,
$x\in W_{\mathrm {aff}}$
,
![]() $y\in W^{\prime }_{\mathrm {aff}}$
and
$y\in W^{\prime }_{\mathrm {aff}}$
and
![]() $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
-
(1)
 $x(\lambda )_A = \lambda _{Ax}$
.
$x(\lambda )_A = \lambda _{Ax}$
. -
(2)
 $y(\lambda _A) = \lambda _{yA}$
.
$y(\lambda _A) = \lambda _{yA}$
. -
(3)
 $\nu ^{A} = x(\nu ^{Ax})$
.
$\nu ^{A} = x(\nu ^{Ax})$
. -
(4)
 $\nu ^A = y(\nu )^{yA}$
.
$\nu ^A = y(\nu )^{yA}$
.
Fix a positive system
![]() $\Delta ^+ \subset \Delta $
. Let
$\Delta ^+ \subset \Delta $
. Let
![]() $\alpha \in \Delta ^+$
and
$\alpha \in \Delta ^+$
and
![]() $n\in {\mathbb {Z}}$
. We say
$n\in {\mathbb {Z}}$
. We say
![]() $A\le s_{\alpha ,n}(A)$
if, for all
$A\le s_{\alpha ,n}(A)$
if, for all
![]() $a\in A$
, we have
$a\in A$
, we have
![]() $\langle a,\alpha ^\vee \rangle < n$
. The generic Bruhat order
$\langle a,\alpha ^\vee \rangle < n$
. The generic Bruhat order
![]() $\le $
on
$\le $
on
![]() $\mathcal {A}$
is the partial order generated by the relations
$\mathcal {A}$
is the partial order generated by the relations
![]() $A\le s_{\alpha ,n}(A)$
. The following lemma is obvious from the definition.
$A\le s_{\alpha ,n}(A)$
. The following lemma is obvious from the definition.
Lemma 2.2. Let
![]() $A\in \mathcal {A}$
,
$A\in \mathcal {A}$
,
![]() $w\in W^{\prime }_{{\mathrm {aff}}}$
and a is in the closure of A. If
$w\in W^{\prime }_{{\mathrm {aff}}}$
and a is in the closure of A. If
![]() $A \le w(A)$
, then
$A \le w(A)$
, then
![]() $w(a) - a\in {\mathbb {R}}_{\ge 0}\Delta ^+$
.
$w(a) - a\in {\mathbb {R}}_{\ge 0}\Delta ^+$
.
Lemma 2.3. Let
![]() $A,A'\in \mathcal {A}$
such that
$A,A'\in \mathcal {A}$
such that
![]() $A + \nu = A'$
for
$A + \nu = A'$
for
![]() $\nu \in {\mathbb {Z}}\Delta $
. Then,
$\nu \in {\mathbb {Z}}\Delta $
. Then,
![]() $A\le A'$
if and only if
$A\le A'$
if and only if
![]() $\nu \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
.
$\nu \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
.
Proof. We assume
![]() $\nu \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
and prove that
$\nu \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
and prove that
![]() $A\le A'$
. We may assume
$A\le A'$
. We may assume
![]() $\nu = \alpha \in \Delta ^+$
. Take
$\nu = \alpha \in \Delta ^+$
. Take
![]() $n\in {\mathbb {Z}}$
such that
$n\in {\mathbb {Z}}$
such that
![]() $n - 1 < \langle a,\alpha ^\vee \rangle < n$
for any
$n - 1 < \langle a,\alpha ^\vee \rangle < n$
for any
![]() $a\in A$
. For
$a\in A$
. For
![]() $a\in A$
, we have
$a\in A$
, we have
![]() $\langle s_{\alpha ,n}(a),\alpha ^\vee \rangle = \langle a - (\langle a,\alpha ^\vee \rangle - n)\alpha ,\alpha ^\vee \rangle = 2n - \langle a,\alpha ^\vee \rangle $
. Hence,
$\langle s_{\alpha ,n}(a),\alpha ^\vee \rangle = \langle a - (\langle a,\alpha ^\vee \rangle - n)\alpha ,\alpha ^\vee \rangle = 2n - \langle a,\alpha ^\vee \rangle $
. Hence,
![]() $n < \langle s_{\alpha ,n}(a),\alpha ^\vee \rangle < n + 1$
. Therefore,
$n < \langle s_{\alpha ,n}(a),\alpha ^\vee \rangle < n + 1$
. Therefore,
![]() $A \le s_{\alpha ,n}(A)\le s_{\alpha ,n + 1}s_{\alpha ,n}(A) = A + \alpha $
.
$A \le s_{\alpha ,n}(A)\le s_{\alpha ,n + 1}s_{\alpha ,n}(A) = A + \alpha $
.
However, assume that
![]() $A\le A'$
. Take
$A\le A'$
. Take
![]() $a\in A$
. Then by Lemma 2.2, we have
$a\in A$
. Then by Lemma 2.2, we have
![]() $(a + \nu ) - a \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. Hence,
$(a + \nu ) - a \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. Hence,
![]() $\nu \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. Since
$\nu \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. Since
![]() $\nu \in {\mathbb {Z}}\Delta $
, we get
$\nu \in {\mathbb {Z}}\Delta $
, we get
![]() $\nu \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
.
$\nu \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
.
A subset
![]() $I\subset \mathcal {A}$
is called open (resp. closed) if
$I\subset \mathcal {A}$
is called open (resp. closed) if
![]() $A\in I$
,
$A\in I$
,
![]() $A'\le A$
(resp.
$A'\le A$
(resp.
![]() $A'\ge A$
), which implies
$A'\ge A$
), which implies
![]() $A'\in I$
. This defines a topology on
$A'\in I$
. This defines a topology on
![]() $\mathcal {A}$
. The following lemma is an immediate result of the previous lemma, and it plays an important role throughout this paper.
$\mathcal {A}$
. The following lemma is an immediate result of the previous lemma, and it plays an important role throughout this paper.
Lemma 2.4. For each
![]() $\Omega \in \mathcal {A}/\Lambda _{\mathrm {aff}}$
and
$\Omega \in \mathcal {A}/\Lambda _{\mathrm {aff}}$
and
![]() $x\in W_{{\mathrm {aff}}}$
, the map
$x\in W_{{\mathrm {aff}}}$
, the map
![]() $x\colon \Omega \to \Omega x$
preserves the order.
$x\colon \Omega \to \Omega x$
preserves the order.
For
![]() $A,A'\in \mathcal {A}$
, set
$A,A'\in \mathcal {A}$
, set
![]() $[A,A'] = \{A"\in \mathcal {A}\mid A\le A"\le A'\}$
. For
$[A,A'] = \{A"\in \mathcal {A}\mid A\le A"\le A'\}$
. For
![]() $\alpha \in \Delta ^+$
and
$\alpha \in \Delta ^+$
and
![]() $A\in \mathcal {A}$
, take
$A\in \mathcal {A}$
, take
![]() $n\in {\mathbb {Z}}$
such that
$n\in {\mathbb {Z}}$
such that
![]() $n - 1 < \langle a,\alpha ^\vee \rangle < n$
for all
$n - 1 < \langle a,\alpha ^\vee \rangle < n$
for all
![]() $a\in A$
and define
$a\in A$
and define
![]() $\alpha \uparrow A = s_{\alpha ,n}(A)$
. By the definition,
$\alpha \uparrow A = s_{\alpha ,n}(A)$
. By the definition,
![]() $A\le \alpha \uparrow A$
. We define
$A\le \alpha \uparrow A$
. We define
![]() $\alpha \downarrow A$
as the unique element such that
$\alpha \downarrow A$
as the unique element such that
![]() $\alpha \uparrow (\alpha \downarrow A) = A$
.
$\alpha \uparrow (\alpha \downarrow A) = A$
.
In this paper, graded module (resp. ring) means
![]() ${\mathbb {Z}}$
-graded module (resp. ring). Let
${\mathbb {Z}}$
-graded module (resp. ring). Let
![]() $M = \bigoplus _i M^i$
be a graded module. For
$M = \bigoplus _i M^i$
be a graded module. For
![]() $k\in {\mathbb {Z}}$
, we define
$k\in {\mathbb {Z}}$
, we define
![]() $M(k)$
by
$M(k)$
by
![]() $M(k)^i = M^{i + k}$
. For a graded ring S, a graded S-module M is called graded free if it is isomorphic to
$M(k)^i = M^{i + k}$
. For a graded ring S, a graded S-module M is called graded free if it is isomorphic to
![]() $\bigoplus _i S(n_i)$
where
$\bigoplus _i S(n_i)$
where
![]() $n_1,\dots ,n_r\in {\mathbb {Z}}$
(in this paper, graded free means graded free of finite rank). We set
$n_1,\dots ,n_r\in {\mathbb {Z}}$
(in this paper, graded free means graded free of finite rank). We set
![]() $\operatorname {\mathrm {grk}}(M) = \sum _{i}v^{n_i}\in {\mathbb {Z}}[v,v^{-1}]$
, where v is an indeterminate.
$\operatorname {\mathrm {grk}}(M) = \sum _{i}v^{n_i}\in {\mathbb {Z}}[v,v^{-1}]$
, where v is an indeterminate.
2.2 The categories
Fix a Noetherian integral domain
![]() ${\mathbb {K}}$
(in the Introduction, it was an algebraically closed field. Since our arguments work with a Noetherian integral domain, we assume
${\mathbb {K}}$
(in the Introduction, it was an algebraically closed field. Since our arguments work with a Noetherian integral domain, we assume
![]() ${\mathbb {K}}$
is a Noetherian integral domain. Later we will add more assumptions). We define
${\mathbb {K}}$
is a Noetherian integral domain. Later we will add more assumptions). We define
![]() $\Lambda ^\vee $
using
$\Lambda ^\vee $
using
![]() $X^\vee $
exactly in the same way as we defined
$X^\vee $
exactly in the same way as we defined
![]() $\Lambda $
using X. As
$\Lambda $
using X. As
![]() $\Lambda $
,
$\Lambda $
,
![]() $W_{{\mathrm {aff}}}$
acts on
$W_{{\mathrm {aff}}}$
acts on
![]() $\Lambda ^{\vee }$
. We put
$\Lambda ^{\vee }$
. We put
![]() $\Lambda ^\vee _{{\mathbb {K}}} = \Lambda ^\vee \otimes _{{\mathbb {Z}}}{\mathbb {K}}$
,
$\Lambda ^\vee _{{\mathbb {K}}} = \Lambda ^\vee \otimes _{{\mathbb {Z}}}{\mathbb {K}}$
,
![]() $X^\vee _{{\mathbb {K}}} = X^\vee \otimes _{{\mathbb {Z}}}{\mathbb {K}}$
and
$X^\vee _{{\mathbb {K}}} = X^\vee \otimes _{{\mathbb {Z}}}{\mathbb {K}}$
and
![]() $R = \operatorname {\mathrm {Sym}}(\Lambda ^\vee _{{\mathbb {K}}})$
. The algebra R is equipped with a grading such that
$R = \operatorname {\mathrm {Sym}}(\Lambda ^\vee _{{\mathbb {K}}})$
. The algebra R is equipped with a grading such that
![]() $\deg (\Lambda ^\vee _{{\mathbb {K}}}) = 2$
. As for the case of
$\deg (\Lambda ^\vee _{{\mathbb {K}}}) = 2$
. As for the case of
![]() $\Lambda $
and X, for
$\Lambda $
and X, for
![]() $f\in \Lambda ^{\vee }$
, we put
$f\in \Lambda ^{\vee }$
, we put
![]() $f_{A} = f(A)$
. Then,
$f_{A} = f(A)$
. Then,
![]() $f\mapsto f_{A}$
gives an isomorphism
$f\mapsto f_{A}$
gives an isomorphism
![]() $\Lambda ^{\vee }\to X^{\vee }$
and this induces an isomorphism
$\Lambda ^{\vee }\to X^{\vee }$
and this induces an isomorphism
![]() $R\to S$
for which we also write
$R\to S$
for which we also write
![]() $f\mapsto f_{A}$
. The inverse of this map is denoted by
$f\mapsto f_{A}$
. The inverse of this map is denoted by
![]() $g\mapsto g^{A}$
.
$g\mapsto g^{A}$
.
Assumption 2.5. In the rest of this section, we assume the following.
-
(1) We have
 $2\in {\mathbb {K}}^\times $
, and any
$2\in {\mathbb {K}}^\times $
, and any
 $\alpha ^\vee \ne \beta ^\vee \in (\Delta ^\vee )^+$
are linearly independent in
$\alpha ^\vee \ne \beta ^\vee \in (\Delta ^\vee )^+$
are linearly independent in
 $X^\vee _{{\mathbb {K}}/\mathfrak {m}}$
for any maximal ideal
$X^\vee _{{\mathbb {K}}/\mathfrak {m}}$
for any maximal ideal
 $\mathfrak {m}\subset {\mathbb {K}}$
. This is the GKM-property of the moment graph attached to the finite Weyl group [Reference FiebigFie11, 9.1].
$\mathfrak {m}\subset {\mathbb {K}}$
. This is the GKM-property of the moment graph attached to the finite Weyl group [Reference FiebigFie11, 9.1]. -
(2) The torsion primes of the root system
 $(X^\vee ,\Delta ^\vee ,X,\Delta )$
[Reference Juteau, Mautner and WilliamsonJMW14, Definition 2.43] are invertible in
$(X^\vee ,\Delta ^\vee ,X,\Delta )$
[Reference Juteau, Mautner and WilliamsonJMW14, Definition 2.43] are invertible in
 ${\mathbb {K}}$
.
${\mathbb {K}}$
.
Lemma 2.6. The representation
![]() $X^\vee _{{\mathbb {K}}}$
of
$X^\vee _{{\mathbb {K}}}$
of
![]() $W_{\mathrm {f}}$
is faithful.
$W_{\mathrm {f}}$
is faithful.
Proof. If
![]() $w\in W_{\mathrm {f}}$
fixes any element in
$w\in W_{\mathrm {f}}$
fixes any element in
![]() $X^\vee _{{\mathbb {K}}}$
, it fixes any image of
$X^\vee _{{\mathbb {K}}}$
, it fixes any image of
![]() $\alpha \in \Delta $
. By the assumption,
$\alpha \in \Delta $
. By the assumption,
![]() $\Delta ^\vee \to X^\vee _{{\mathbb {K}}}$
is injective. Therefore, w fixes any coroot. Hence, w is identity.
$\Delta ^\vee \to X^\vee _{{\mathbb {K}}}$
is injective. Therefore, w fixes any coroot. Hence, w is identity.
The image of
![]() $\alpha ^\vee \in \Delta ^\vee $
in
$\alpha ^\vee \in \Delta ^\vee $
in
![]() $X^\vee _{{\mathbb {K}}}$
is denoted by the same letter. We also put
$X^\vee _{{\mathbb {K}}}$
is denoted by the same letter. We also put
![]() $S = \operatorname {\mathrm {Sym}}(X^\vee _{{\mathbb {K}}})$
. We give a grading to S via
$S = \operatorname {\mathrm {Sym}}(X^\vee _{{\mathbb {K}}})$
. We give a grading to S via
![]() $\deg (X^\vee _{{\mathbb {K}}}) = 2$
. Set
$\deg (X^\vee _{{\mathbb {K}}}) = 2$
. Set
![]() $S^\emptyset = S[(\alpha ^\vee )^{-1}\mid \alpha \in \Delta ]$
. For an S-module M, set
$S^\emptyset = S[(\alpha ^\vee )^{-1}\mid \alpha \in \Delta ]$
. For an S-module M, set
![]() $M^\emptyset = S^\emptyset \otimes _{S} M$
. If M is an S-algebra, then
$M^\emptyset = S^\emptyset \otimes _{S} M$
. If M is an S-algebra, then
![]() $M^{\emptyset }$
is an
$M^{\emptyset }$
is an
![]() $S^{\emptyset }$
-algebra. Let
$S^{\emptyset }$
-algebra. Let
![]() $S_0$
be a flat commutative graded S-algebra. If M is an
$S_0$
be a flat commutative graded S-algebra. If M is an
![]() $S_{0}$
-module, then
$S_{0}$
-module, then
![]() $M^{\emptyset } \simeq S_{0}^{\emptyset }\otimes _{S_{0}}M$
is an
$M^{\emptyset } \simeq S_{0}^{\emptyset }\otimes _{S_{0}}M$
is an
![]() $S_{0}^{\emptyset }$
-module. We consider the category
$S_{0}^{\emptyset }$
-module. We consider the category
![]() $\widetilde {\mathcal {K}}'(S_0)$
consisting of
$\widetilde {\mathcal {K}}'(S_0)$
consisting of
![]() $M = (M,\{M^{\emptyset }_{A}\}_{A\in \mathcal {A}})$
such that
$M = (M,\{M^{\emptyset }_{A}\}_{A\in \mathcal {A}})$
such that
-
• M is a graded
 $(S_0,R)$
-bimodule which is finitely generated torsion-free as a left
$(S_0,R)$
-bimodule which is finitely generated torsion-free as a left
 $S_0$
-module.
$S_0$
-module. -
•
 $M^{\emptyset }_{A}$
is an
$M^{\emptyset }_{A}$
is an
 $(S_0^{\emptyset },R)$
-bimodule such that
$(S_0^{\emptyset },R)$
-bimodule such that
 $mf = f_Am$
for any
$mf = f_Am$
for any
 $m\in M^{\emptyset }_{A}$
and
$m\in M^{\emptyset }_{A}$
and
 $f\in R$
.
$f\in R$
. -
•
 $M^\emptyset = \bigoplus _{A\in \mathcal {A}}M^{\emptyset }_{A}$
.
$M^\emptyset = \bigoplus _{A\in \mathcal {A}}M^{\emptyset }_{A}$
.
A morphism
![]() $M\to N$
in
$M\to N$
in
![]() $\widetilde {\mathcal {K}}'(S_{0})$
is an
$\widetilde {\mathcal {K}}'(S_{0})$
is an
![]() $(S_0,R)$
-bimodule
$(S_0,R)$
-bimodule
![]() $\varphi $
homomorphism of degree zero such that
$\varphi $
homomorphism of degree zero such that
for any
![]() $A\in \mathcal {A}$
. We put
$A\in \mathcal {A}$
. We put
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(M,N) = \bigoplus _i \operatorname {\mathrm {Hom}}_{\widetilde {\mathcal {K}}'(S_0)}(M,N(i))$
. This is a graded
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(M,N) = \bigoplus _i \operatorname {\mathrm {Hom}}_{\widetilde {\mathcal {K}}'(S_0)}(M,N(i))$
. This is a graded
![]() $(S_{0},R)$
-bimodule. For
$(S_{0},R)$
-bimodule. For
![]() $M\in \widetilde {\mathcal {K}}'(S_0)$
, we put
$M\in \widetilde {\mathcal {K}}'(S_0)$
, we put
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M) = \{A\in \mathcal {A}\mid M_A^{\emptyset }\ne 0\}$
.
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M) = \{A\in \mathcal {A}\mid M_A^{\emptyset }\ne 0\}$
.
Remark 2.7. Let
![]() $\Omega \in \mathcal {A}/\Lambda _{{\mathrm {aff}}}$
. For any
$\Omega \in \mathcal {A}/\Lambda _{{\mathrm {aff}}}$
. For any
![]() $m\in \bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
and
$m\in \bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
and
![]() $f\in R$
, we have
$f\in R$
, we have
![]() $mf = f_{\Omega }m$
. The action of
$mf = f_{\Omega }m$
. The action of
![]() $W^{\prime }_{{\mathrm {aff}}}$
on
$W^{\prime }_{{\mathrm {aff}}}$
on
![]() $\mathcal {A}/\Lambda _{{\mathrm {aff}}}$
factors through
$\mathcal {A}/\Lambda _{{\mathrm {aff}}}$
factors through
![]() $W^{\prime }_{{\mathrm {aff}}}\to W_{\mathrm {f}}$
, and
$W^{\prime }_{{\mathrm {aff}}}\to W_{\mathrm {f}}$
, and
![]() $W_{\mathrm {f}}$
acts on
$W_{\mathrm {f}}$
acts on
![]() $\mathcal {A}/\Lambda _{{\mathrm {aff}}}$
simply transitively. We have
$\mathcal {A}/\Lambda _{{\mathrm {aff}}}$
simply transitively. We have
![]() $M^{\emptyset } = \bigoplus _{w\in W_{\mathrm {f}}}(\bigoplus _{A\in w(\Omega )}M_{A}^{\emptyset })$
and for
$M^{\emptyset } = \bigoplus _{w\in W_{\mathrm {f}}}(\bigoplus _{A\in w(\Omega )}M_{A}^{\emptyset })$
and for
![]() $m\in \bigoplus _{A\in w(\Omega )}M_{A}^{\emptyset }$
,
$m\in \bigoplus _{A\in w(\Omega )}M_{A}^{\emptyset }$
,
![]() $mf = w(f_{\Omega })m$
. Therefore, the decomposition of
$mf = w(f_{\Omega })m$
. Therefore, the decomposition of
![]() $M^{\emptyset }$
into
$M^{\emptyset }$
into
![]() $\bigoplus _{A\in w(\Omega )}M_{A}^{\emptyset }$
is determined by the
$\bigoplus _{A\in w(\Omega )}M_{A}^{\emptyset }$
is determined by the
![]() $(S_0,R)$
-bimodule structure. Hence, any
$(S_0,R)$
-bimodule structure. Hence, any
![]() $(S_0,R)$
-bimodule homomorphism
$(S_0,R)$
-bimodule homomorphism
![]() $M\to N$
sends
$M\to N$
sends
![]() $\bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
to
$\bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
to
![]() $\bigoplus _{A\in \Omega }N_{A}^{\emptyset }$
. We will often use this fact.
$\bigoplus _{A\in \Omega }N_{A}^{\emptyset }$
. We will often use this fact.
Remark 2.8. Here, we do not assume that a morphism
![]() $M\to N$
in
$M\to N$
in
![]() $\widetilde {\mathcal {K}}'(S_{0})$
sends
$\widetilde {\mathcal {K}}'(S_{0})$
sends
![]() $M_A^{\emptyset }$
to
$M_A^{\emptyset }$
to
![]() $N^{\emptyset }_{A}$
.
$N^{\emptyset }_{A}$
.
For each closed subset
![]() $I\subset \mathcal {A}$
, we define
$I\subset \mathcal {A}$
, we define
![]() $M_{I} = M\cap \bigoplus _{A\in I}M_A^{\emptyset }$
. Set
$M_{I} = M\cap \bigoplus _{A\in I}M_A^{\emptyset }$
. Set
 $$\begin{align*}(M_{I})_{A}^{\emptyset} = \begin{cases} M_{A}^{\emptyset} & (A\in I),\\ 0 & (A\notin I). \end{cases} \end{align*}$$
$$\begin{align*}(M_{I})_{A}^{\emptyset} = \begin{cases} M_{A}^{\emptyset} & (A\in I),\\ 0 & (A\notin I). \end{cases} \end{align*}$$
By the following lemma,
![]() $M_{I}\in \widetilde {\mathcal {K}}'(S_0)$
and therefore,
$M_{I}\in \widetilde {\mathcal {K}}'(S_0)$
and therefore,
![]() $M\mapsto M_{I}$
is an endofunctor of
$M\mapsto M_{I}$
is an endofunctor of
![]() $\widetilde {\mathcal {K}}'(S_0)$
. We have a natural monomorphism
$\widetilde {\mathcal {K}}'(S_0)$
. We have a natural monomorphism
![]() $M_{I}\to M$
in
$M_{I}\to M$
in
![]() $\widetilde {\mathcal {K}}'(S_{0})$
.
$\widetilde {\mathcal {K}}'(S_{0})$
.
Lemma 2.9. The module
![]() $M_I$
is an
$M_I$
is an
![]() $(R_{0},S)$
-submodule of M, and we have
$(R_{0},S)$
-submodule of M, and we have
We also have
![]() $M_{I_1\cap I_2} = M_{I_1}\cap M_{I_2}$
for any closed subsets
$M_{I_1\cap I_2} = M_{I_1}\cap M_{I_2}$
for any closed subsets
![]() $I_{1},I_{2}\subset \mathcal {A}$
.
$I_{1},I_{2}\subset \mathcal {A}$
.
Proof. The first part is obvious, and for the second part, the left-hand side is contained in the right-hand side. Take m from the right-hand side and let
![]() $f\in S$
such that
$f\in S$
such that
![]() $fm\in M$
. Then, we have
$fm\in M$
. Then, we have
![]() $fm\in M_{I}$
, and m is in the left-hand side. The last assertion is obvious.
$fm\in M_{I}$
, and m is in the left-hand side. The last assertion is obvious.
If
![]() $S^{\prime }_{0}$
is a commutative flat graded
$S^{\prime }_{0}$
is a commutative flat graded
![]() $S_{0}$
-algebra, then for
$S_{0}$
-algebra, then for
![]() $M\in \widetilde {\mathcal {K}}'(S_{0})$
, the
$M\in \widetilde {\mathcal {K}}'(S_{0})$
, the
![]() $(S_{0}',R)$
-bimodule
$(S_{0}',R)$
-bimodule
![]() $S_{0}'\otimes _{S_{0}}M$
has a decomposition
$S_{0}'\otimes _{S_{0}}M$
has a decomposition
![]() $(S^{\prime }_{0}\otimes _{S_{0}} M)^{\emptyset }\simeq \bigoplus _{A\in \mathcal {A}}((S^{\prime }_{0})^{\emptyset }\otimes _{S_{0}^{\emptyset }}M_{A}^{\emptyset })$
, and this decomposition gives a structure of an object in
$(S^{\prime }_{0}\otimes _{S_{0}} M)^{\emptyset }\simeq \bigoplus _{A\in \mathcal {A}}((S^{\prime }_{0})^{\emptyset }\otimes _{S_{0}^{\emptyset }}M_{A}^{\emptyset })$
, and this decomposition gives a structure of an object in
![]() $\widetilde {\mathcal {K}}'(S^{\prime }_{0})$
. It is easy to see that
$\widetilde {\mathcal {K}}'(S^{\prime }_{0})$
. It is easy to see that
![]() $M\mapsto S^{\prime }_{0}\otimes _{S_{0}}M$
is a functor
$M\mapsto S^{\prime }_{0}\otimes _{S_{0}}M$
is a functor
![]() $\widetilde {\mathcal {K}}'(S_{0})\to \widetilde {\mathcal {K}}'(S^{\prime }_{0})$
.
$\widetilde {\mathcal {K}}'(S_{0})\to \widetilde {\mathcal {K}}'(S^{\prime }_{0})$
.
For each
![]() $\alpha \in \Delta $
, set
$\alpha \in \Delta $
, set
![]() $W_{\alpha ,{\mathrm {aff}}}' = \{1,s_{\alpha }\}\ltimes {\mathbb {Z}}\alpha \subset W_{{\mathrm {aff}}}'$
. We also put
$W_{\alpha ,{\mathrm {aff}}}' = \{1,s_{\alpha }\}\ltimes {\mathbb {Z}}\alpha \subset W_{{\mathrm {aff}}}'$
. We also put
![]() $S^{\alpha } = S[(\beta ^\vee )^{-1}\mid \beta \in \Delta \setminus \{\pm \alpha \}]$
and
$S^{\alpha } = S[(\beta ^\vee )^{-1}\mid \beta \in \Delta \setminus \{\pm \alpha \}]$
and
![]() $M^\alpha = S^{\alpha }\otimes _S M$
for any left S-module M. Again, if M is an S-algebra then
$M^\alpha = S^{\alpha }\otimes _S M$
for any left S-module M. Again, if M is an S-algebra then
![]() $M^{\alpha }$
is an
$M^{\alpha }$
is an
![]() $S^{\alpha }$
-algebra. If
$S^{\alpha }$
-algebra. If
![]() $M\in \widetilde {\mathcal {K}}'(S_{0})$
, then
$M\in \widetilde {\mathcal {K}}'(S_{0})$
, then
![]() $M^{\alpha }\in \widetilde {\mathcal {K}}'(S_{0}^{\alpha })$
as mentioned above. Note that, from our assumption,
$M^{\alpha }\in \widetilde {\mathcal {K}}'(S_{0}^{\alpha })$
as mentioned above. Note that, from our assumption,
![]() $\bigcap _{\alpha \in \Delta ^+}S^{\alpha } = S$
[Reference Andersen, Jantzen and SoergelAJS94, 9.1 Lemma]. We say
$\bigcap _{\alpha \in \Delta ^+}S^{\alpha } = S$
[Reference Andersen, Jantzen and SoergelAJS94, 9.1 Lemma]. We say
![]() $M\in \widetilde {\mathcal {K}}(S_0)$
if
$M\in \widetilde {\mathcal {K}}(S_0)$
if
![]() $M\in \widetilde {\mathcal {K}}'(S_0)$
and satisfies the following two conditions which are taken from [Reference Fiebig and LaniniFL15]. These are important properties in our arguments.
$M\in \widetilde {\mathcal {K}}'(S_0)$
and satisfies the following two conditions which are taken from [Reference Fiebig and LaniniFL15]. These are important properties in our arguments.
-
(S)
 $M_{I_1\cup I_2} = M_{I_1} + M_{I_2}$
for any two closed subsets
$M_{I_1\cup I_2} = M_{I_1} + M_{I_2}$
for any two closed subsets
 $I_1,I_2$
.
$I_1,I_2$
. -
(LE) For any
 $\alpha \in \Delta ^{+}$
, there exist
$\alpha \in \Delta ^{+}$
, there exist
 $M^{(\Omega )}\in \widetilde {\mathcal {K}}'(S_{0}^{\alpha })$
for all
$M^{(\Omega )}\in \widetilde {\mathcal {K}}'(S_{0}^{\alpha })$
for all
 $\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
with an injective morphism
$\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
with an injective morphism
 $M^{(\Omega )}\hookrightarrow M^{\alpha }$
in
$M^{(\Omega )}\hookrightarrow M^{\alpha }$
in
 $\widetilde {\mathcal {K}}'(S_0^{\alpha })$
such that
$\widetilde {\mathcal {K}}'(S_0^{\alpha })$
such that
 $\operatorname {\mathrm {supp}}_{\mathcal {A}}M^{(\Omega )}\subset \Omega $
and the induced morphism
$\operatorname {\mathrm {supp}}_{\mathcal {A}}M^{(\Omega )}\subset \Omega $
and the induced morphism
 $\bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}M^{(\Omega )}\to M^{\alpha }$
is an isomorphism in
$\bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}M^{(\Omega )}\to M^{\alpha }$
is an isomorphism in
 $\widetilde {\mathcal {K}}'(S_0^{\alpha })$
.
$\widetilde {\mathcal {K}}'(S_0^{\alpha })$
. -
(S) stands for “sheaf” and (LE) stands for “local extension condition” [Reference Fiebig and LaniniFL15, Definition 5.4].
Let
![]() $M\in \widetilde {\mathcal {K}}'(S_{0})$
. If
$M\in \widetilde {\mathcal {K}}'(S_{0})$
. If
![]() $M^{\alpha } = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }M^{\emptyset }_{A}\cap M^{\alpha })$
for any
$M^{\alpha } = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }M^{\emptyset }_{A}\cap M^{\alpha })$
for any
![]() $\alpha \in \Delta $
, M satisfies (LE). The converse is not true, in general. For example, assume
$\alpha \in \Delta $
, M satisfies (LE). The converse is not true, in general. For example, assume
![]() $\#\Delta> 1$
. Fix
$\#\Delta> 1$
. Fix
![]() $\alpha \in \Delta ^{+}$
. Take
$\alpha \in \Delta ^{+}$
. Take
![]() $\beta \in \Delta ^{+}\setminus \{\alpha \}$
and
$\beta \in \Delta ^{+}\setminus \{\alpha \}$
and
![]() $A\in \mathcal {A}$
. Define
$A\in \mathcal {A}$
. Define
![]() $N\in \widetilde {\mathcal {K}}'(S)$
by
$N\in \widetilde {\mathcal {K}}'(S)$
by
![]() $N = \{(f,g)\mid f,g\in S,f\equiv g\pmod {\alpha }\}$
,
$N = \{(f,g)\mid f,g\in S,f\equiv g\pmod {\alpha }\}$
,
![]() $N_{A}^{\emptyset } = S^{\emptyset }\oplus 0$
,
$N_{A}^{\emptyset } = S^{\emptyset }\oplus 0$
,
![]() $N_{A - \beta }^{\emptyset } = 0\oplus S^{\emptyset }$
and
$N_{A - \beta }^{\emptyset } = 0\oplus S^{\emptyset }$
and
![]() $N_{A'}^{\emptyset } = 0$
for any
$N_{A'}^{\emptyset } = 0$
for any
![]() $A'\in \mathcal {A}\setminus \{A,A - \beta \}$
(these determine the right R-action on N uniquely). Then, it is easy to see that
$A'\in \mathcal {A}\setminus \{A,A - \beta \}$
(these determine the right R-action on N uniquely). Then, it is easy to see that
![]() $N^{\alpha } \ne \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }N^{\emptyset }_{A}\cap N^{\alpha })$
. Define
$N^{\alpha } \ne \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }N^{\emptyset }_{A}\cap N^{\alpha })$
. Define
![]() $N^{(\Omega )}\in \widetilde {\mathcal {K}}'(S)$
for
$N^{(\Omega )}\in \widetilde {\mathcal {K}}'(S)$
for
![]() $\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
as follows:
$\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
as follows:
![]() $N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)} = S^{\alpha }$
,
$N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)} = S^{\alpha }$
,
![]() $(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)})^{\emptyset }_{A} = S^{\emptyset }$
,
$(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)})^{\emptyset }_{A} = S^{\emptyset }$
,
![]() $(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)})^{\emptyset }_{A'} = 0$
for
$(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)})^{\emptyset }_{A'} = 0$
for
![]() $A'\in \mathcal {A}\setminus \{A\}$
,
$A'\in \mathcal {A}\setminus \{A\}$
,
![]() $N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))} = S^{\alpha }$
,
$N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))} = S^{\alpha }$
,
![]() $(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))})^{\emptyset }_{A - \beta } = S^{\emptyset }$
,
$(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))})^{\emptyset }_{A - \beta } = S^{\emptyset }$
,
![]() $(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))})^{\emptyset }_{A'} = S^{\emptyset }$
for
$(N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))})^{\emptyset }_{A'} = S^{\emptyset }$
for
![]() $A'\in \mathcal {A}\setminus \{A - \beta \}$
and
$A'\in \mathcal {A}\setminus \{A - \beta \}$
and
![]() $N^{(\Omega )} = 0$
for
$N^{(\Omega )} = 0$
for
![]() $\Omega \ne W^{\prime }_{\alpha ,{\mathrm {aff}}}A,W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta )$
. Then, we have
$\Omega \ne W^{\prime }_{\alpha ,{\mathrm {aff}}}A,W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta )$
. Then, we have
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}} N^{(\Omega )}\subset \Omega $
. We define
$\operatorname {\mathrm {supp}}_{\mathcal {A}} N^{(\Omega )}\subset \Omega $
. We define
![]() $N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}\to N^{\alpha }$
(resp.
$N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}\to N^{\alpha }$
(resp.
![]() $N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))}\to N^{\alpha }$
) by
$N^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}(A - \beta ))}\to N^{\alpha }$
) by
![]() $f\mapsto (\alpha f,0)$
(resp.
$f\mapsto (\alpha f,0)$
(resp.
![]() $f\mapsto (f,f)$
). Then,
$f\mapsto (f,f)$
). Then,
![]() $\bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}N^{(\Omega )}\to N^{\alpha }$
is an isomorphism. We can also easily verify that
$\bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}N^{(\Omega )}\to N^{\alpha }$
is an isomorphism. We can also easily verify that
![]() $N^{\gamma } = \bigoplus _{\Omega \in W^{\prime }_{\gamma ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }N_{A}^{\emptyset }\cap N^{\gamma })$
for any
$N^{\gamma } = \bigoplus _{\Omega \in W^{\prime }_{\gamma ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }N_{A}^{\emptyset }\cap N^{\gamma })$
for any
![]() $\gamma \in \Delta ^{+}\setminus \{\alpha \}$
. Hence, N satisfies (LE).
$\gamma \in \Delta ^{+}\setminus \{\alpha \}$
. Hence, N satisfies (LE).
We have the following. M satisfies (LE) if and only if for any
![]() $\alpha \in \Delta $
, there exists
$\alpha \in \Delta $
, there exists
![]() $N\in \widetilde {\mathcal {K}}'(S_0^{\alpha })$
which is isomorphic to
$N\in \widetilde {\mathcal {K}}'(S_0^{\alpha })$
which is isomorphic to
![]() $M^{\alpha }$
and satisfies
$M^{\alpha }$
and satisfies
![]() $N = \bigoplus _{\Omega \in W_{\alpha ,{\mathrm {aff}}}'\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }N^{\emptyset }_{A}\cap N)$
.
$N = \bigoplus _{\Omega \in W_{\alpha ,{\mathrm {aff}}}'\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }N^{\emptyset }_{A}\cap N)$
.
Lemma 2.10. Let
![]() $M\in \widetilde {\mathcal {K}}'(S_0)$
,
$M\in \widetilde {\mathcal {K}}'(S_0)$
,
![]() $\alpha \in \Delta $
and
$\alpha \in \Delta $
and
![]() $A\in \mathcal {A}$
. Assume that
$A\in \mathcal {A}$
. Assume that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. Then, M satisfies (S). In particular, if M satisfies (LE), then
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. Then, M satisfies (S). In particular, if M satisfies (LE), then
![]() $M^{\alpha }$
satisfies (S).
$M^{\alpha }$
satisfies (S).
Proof. Set
![]() $\Omega = W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
and let
$\Omega = W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
and let
![]() $I_1,I_2\subset \mathcal {A}$
be closed subsets. We have
$I_1,I_2\subset \mathcal {A}$
be closed subsets. We have
![]() $\Omega = \{A,\alpha \uparrow A,\alpha \uparrow (\alpha \uparrow A),\dots \}\cup \{\alpha \downarrow A,\alpha \downarrow (\alpha \downarrow A),\dots \}$
and
$\Omega = \{A,\alpha \uparrow A,\alpha \uparrow (\alpha \uparrow A),\dots \}\cup \{\alpha \downarrow A,\alpha \downarrow (\alpha \downarrow A),\dots \}$
and
![]() $\Omega $
is a totally ordered subset of
$\Omega $
is a totally ordered subset of
![]() $\mathcal {A}$
. Since
$\mathcal {A}$
. Since
![]() $\Omega $
is totally ordered,
$\Omega $
is totally ordered,
![]() $I_1\cap \Omega \subset I_2\cap \Omega $
or
$I_1\cap \Omega \subset I_2\cap \Omega $
or
![]() $I_2\cap \Omega \subset I_1\cap \Omega $
. We may assume
$I_2\cap \Omega \subset I_1\cap \Omega $
. We may assume
![]() $I_1\cap \Omega \subset I_2\cap \Omega $
. We can take closed subsets
$I_1\cap \Omega \subset I_2\cap \Omega $
. We can take closed subsets
![]() $I^{\prime }_1$
and
$I^{\prime }_1$
and
![]() $I^{\prime }_2$
such that
$I^{\prime }_2$
such that
![]() $I^{\prime }_1\subset I^{\prime }_2$
,
$I^{\prime }_1\subset I^{\prime }_2$
,
![]() $I^{\prime }_1\cap \Omega = I_1\cap \Omega $
and
$I^{\prime }_1\cap \Omega = I_1\cap \Omega $
and
![]() $I^{\prime }_2\cap \Omega = I_2\cap \Omega $
. Then, we have
$I^{\prime }_2\cap \Omega = I_2\cap \Omega $
. Then, we have
![]() $M_{I^{\prime }_1} = M_{I_1}$
,
$M_{I^{\prime }_1} = M_{I_1}$
,
![]() $M_{I^{\prime }_2} = M_{I_2}$
and
$M_{I^{\prime }_2} = M_{I_2}$
and
![]() $M_{I^{\prime }_1\cup I^{\prime }_2} = M_{I_1\cup I_2}$
. Hence, we may assume
$M_{I^{\prime }_1\cup I^{\prime }_2} = M_{I_1\cup I_2}$
. Hence, we may assume
![]() $I_1 = I^{\prime }_1$
and
$I_1 = I^{\prime }_1$
and
![]() $I_2 = I^{\prime }_2$
. In this case, (S) obviously holds.
$I_2 = I^{\prime }_2$
. In this case, (S) obviously holds.
Let
![]() $K\subset \mathcal {A}$
be a locally closed subset; namely, K is the intersection of a closed subset I with an open subset J. It is easy to see that, if
$K\subset \mathcal {A}$
be a locally closed subset; namely, K is the intersection of a closed subset I with an open subset J. It is easy to see that, if
![]() $M\in \widetilde {\mathcal {K}}'(S_{0})$
satisfies (S), then
$M\in \widetilde {\mathcal {K}}'(S_{0})$
satisfies (S), then
![]() $M_{I}/M_{I\setminus J}\simeq M_{I'}/M_{I'\setminus J'}$
naturally for closed subsets
$M_{I}/M_{I\setminus J}\simeq M_{I'}/M_{I'\setminus J'}$
naturally for closed subsets
![]() $I,I'$
and open subsets
$I,I'$
and open subsets
![]() $J,J'$
such that
$J,J'$
such that
![]() $K = I\cap J = I'\cap J'$
. We define
$K = I\cap J = I'\cap J'$
. We define
![]() $M_{K} = M_{I}/M_{I\setminus J}$
for
$M_{K} = M_{I}/M_{I\setminus J}$
for
![]() $M\in \widetilde {\mathcal {K}}(S_{0})$
. By Lemma 2.9, we have
$M\in \widetilde {\mathcal {K}}(S_{0})$
. By Lemma 2.9, we have
By putting
![]() $(M_K)^{\emptyset }_A$
equal to the image of
$(M_K)^{\emptyset }_A$
equal to the image of
![]() $M_A^{\emptyset }$
in
$M_A^{\emptyset }$
in
![]() $M_{K}^{\emptyset }$
by this isomorphism, we have an object
$M_{K}^{\emptyset }$
by this isomorphism, we have an object
![]() $M_K$
of
$M_K$
of
![]() $\widetilde {\mathcal {K}}'(S_0)$
. The following lemma is obvious.
$\widetilde {\mathcal {K}}'(S_0)$
. The following lemma is obvious.
Lemma 2.11. We have
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_K) = \operatorname {\mathrm {supp}}_{\mathcal {A}}(M)\cap K$
for any locally closed subset
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_K) = \operatorname {\mathrm {supp}}_{\mathcal {A}}(M)\cap K$
for any locally closed subset
![]() $K\subset \mathcal {A}$
.
$K\subset \mathcal {A}$
.
Lemma 2.12. Let
![]() $K_1,K_2\subset \mathcal {A}$
be locally closed subsets. If
$K_1,K_2\subset \mathcal {A}$
be locally closed subsets. If
![]() $M\in \widetilde {\mathcal {K}}(S_{0})$
, then
$M\in \widetilde {\mathcal {K}}(S_{0})$
, then
![]() $(M_{K_1})_{K_2} \simeq M_{K_1\cap K_2}$
$(M_{K_1})_{K_2} \simeq M_{K_1\cap K_2}$
Proof. The proof is divided into 4 steps.
(1) Assume that both
![]() $K_1,K_2$
are closed. Then, the lemma follows from the definitions.
$K_1,K_2$
are closed. Then, the lemma follows from the definitions.
(2) Assume that
![]() $K_1$
is open and
$K_1$
is open and
![]() $K_2$
is closed. Set
$K_2$
is closed. Set
![]() $I_1 = \mathcal {A}\setminus K_1$
. Then, we have
$I_1 = \mathcal {A}\setminus K_1$
. Then, we have
Note that
![]() $M_{K_2}/(M_{K_2}\cap M_{I_1}) = M_{K_2}/M_{K_2\cap I_1} = M_{K_1\cap K_2}$
. There is a canonical embedding from
$M_{K_2}/(M_{K_2}\cap M_{I_1}) = M_{K_2}/M_{K_2\cap I_1} = M_{K_1\cap K_2}$
. There is a canonical embedding from
![]() $M_{K_2}/(M_{K_2}\cap M_{I_1})$
to
$M_{K_2}/(M_{K_2}\cap M_{I_1})$
to
![]() $(M_{K_1})_{K_2}$
. Let
$(M_{K_1})_{K_2}$
. Let
![]() $m\in M$
such that
$m\in M$
such that
![]() $m + M_{I_1}\in \bigoplus _{A\in K_2}(M/M_{I_1})_{A}^{\emptyset }$
. Then,
$m + M_{I_1}\in \bigoplus _{A\in K_2}(M/M_{I_1})_{A}^{\emptyset }$
. Then,
![]() $M_A^{\emptyset }$
-component
$M_A^{\emptyset }$
-component
![]() $m_{A}$
of m is
$m_{A}$
of m is
![]() $0$
for
$0$
for
![]() $A\notin I_1\cup K_2$
. Hence,
$A\notin I_1\cup K_2$
. Hence,
![]() $m\in M_{I_1\cup K_2} = M_{I_1} + M_{K_2}$
. Therefore, the canonical embedding is surjective. We get the lemma.
$m\in M_{I_1\cup K_2} = M_{I_1} + M_{K_2}$
. Therefore, the canonical embedding is surjective. We get the lemma.
(3) Assume that
![]() $K_2$
is closed. Take a closed subset
$K_2$
is closed. Take a closed subset
![]() $I_1$
and an open subset
$I_1$
and an open subset
![]() $J_1$
such that
$J_1$
such that
![]() $K_1 = I_1\cap J_1$
. Then, by (2),
$K_1 = I_1\cap J_1$
. Then, by (2),
![]() $(M_{J_1})_{I_1} \simeq M_{K_1}$
. Hence,
$(M_{J_1})_{I_1} \simeq M_{K_1}$
. Hence,
![]() $(M_{K_1})_{K_2} \simeq ((M_{J_1})_{I_1})_{K_2} = (M_{J_1})_{I_1\cap K_2}$
by (1). This is isomorphic to
$(M_{K_1})_{K_2} \simeq ((M_{J_1})_{I_1})_{K_2} = (M_{J_1})_{I_1\cap K_2}$
by (1). This is isomorphic to
![]() $M_{J_1\cap I_1\cap K_2} = M_{K_1\cap K_2}$
by (2).
$M_{J_1\cap I_1\cap K_2} = M_{K_1\cap K_2}$
by (2).
(4) Now we prove the lemma in general. Let
![]() $I_i$
be a closed subset and
$I_i$
be a closed subset and
![]() $J_i$
be an open subset such that
$J_i$
be an open subset such that
![]() $K_i = I_i \cap J_i$
and put
$K_i = I_i \cap J_i$
and put
![]() $J_i^c = \mathcal {A}\setminus J_i$
for
$J_i^c = \mathcal {A}\setminus J_i$
for
![]() $i = 1,2$
. Then,
$i = 1,2$
. Then,
by (3). We have
![]() $M_{K_1\cap I_2} = M_{I_1\cap I_2}/M_{I_1\cap I_2\cap J_1^c}$
and
$M_{K_1\cap I_2} = M_{I_1\cap I_2}/M_{I_1\cap I_2\cap J_1^c}$
and
![]() $M_{K_1\cap I_2\cap J_2^c} = M_{I_1\cap I_2\cap J_2^c}/M_{I_1\cap I_2\cap J_2^c\cap J_1^c}$
. Hence,
$M_{K_1\cap I_2\cap J_2^c} = M_{I_1\cap I_2\cap J_2^c}/M_{I_1\cap I_2\cap J_2^c\cap J_1^c}$
. Hence,
Since
![]() $M_{I_1\cap I_2\cap J_1^c} + M_{I_1\cap I_2\cap J_2^c} = M_{(I_1\cap I_2\cap J_1^c)\cup (I_2\cap I_2\cap J_2^c)} = M_{(I_1\cap I_2)\setminus (J_1\cap J_2)}$
, we get the lemma.
$M_{I_1\cap I_2\cap J_1^c} + M_{I_1\cap I_2\cap J_2^c} = M_{(I_1\cap I_2\cap J_1^c)\cup (I_2\cap I_2\cap J_2^c)} = M_{(I_1\cap I_2)\setminus (J_1\cap J_2)}$
, we get the lemma.
Lemma 2.13. If
![]() $M\in \widetilde {\mathcal {K}}(S_0)$
, then
$M\in \widetilde {\mathcal {K}}(S_0)$
, then
![]() $M_K\in \widetilde {\mathcal {K}}(S_0)$
.
$M_K\in \widetilde {\mathcal {K}}(S_0)$
.
Proof. Take a closed subset I and an open subset J such that
![]() $K = I \cap J$
.
$K = I \cap J$
.
We prove
![]() $M_{K}$
satisfies (S). Let
$M_{K}$
satisfies (S). Let
![]() $I_1,I_2$
be closed subsets. Since
$I_1,I_2$
be closed subsets. Since
![]() $(M_{K})_{I_i} = M_{K\cap I_i}$
is a quotient of
$(M_{K})_{I_i} = M_{K\cap I_i}$
is a quotient of
![]() $M_{I\cap I_i}$
, it is sufficient to prove that
$M_{I\cap I_i}$
, it is sufficient to prove that
![]() $M_{I\cap I_1}\oplus M_{I\cap I_2}\to (M_{K})_{I_1\cup I_2}$
is surjective. The module
$M_{I\cap I_1}\oplus M_{I\cap I_2}\to (M_{K})_{I_1\cup I_2}$
is surjective. The module
![]() $(M_{K})_{I_1\cup I_2} = M_{K\cap (I_1\cup I_2)}$
is a quotient of
$(M_{K})_{I_1\cup I_2} = M_{K\cap (I_1\cup I_2)}$
is a quotient of
![]() $M_{I\cap (I_1\cup I_2)}$
, and since
$M_{I\cap (I_1\cup I_2)}$
, and since
![]() $M_{I\cap (I_1\cup I_2)} = M_{I\cap I_1} + M_{I\cap I_2}$
, the map is surjective.
$M_{I\cap (I_1\cup I_2)} = M_{I\cap I_1} + M_{I\cap I_2}$
, the map is surjective.
We prove
![]() $M_{K}$
satisfies (LE). We may assume
$M_{K}$
satisfies (LE). We may assume
![]() $M = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }M_{A}^{\emptyset }\cap M^{\alpha })$
. Let
$M = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }M_{A}^{\emptyset }\cap M^{\alpha })$
. Let
![]() $m \in M_{I}^{\alpha }$
. Then, for each
$m \in M_{I}^{\alpha }$
. Then, for each
![]() $\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
, we have
$\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
, we have
![]() $m_{\Omega }\in M^{\alpha }\cap \bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
such that
$m_{\Omega }\in M^{\alpha }\cap \bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
such that
![]() $m = \sum m_{\Omega }$
. Then, for each
$m = \sum m_{\Omega }$
. Then, for each
![]() $A\in \mathcal {A}$
, we have
$A\in \mathcal {A}$
, we have
![]() $m_{A} = (m_{\Omega })_{A}$
, where
$m_{A} = (m_{\Omega })_{A}$
, where
![]() $\Omega $
is the unique
$\Omega $
is the unique
![]() $W^{\prime }_{\alpha ,{\mathrm {aff}}}$
-orbit containing A. Therefore, since
$W^{\prime }_{\alpha ,{\mathrm {aff}}}$
-orbit containing A. Therefore, since
![]() $m\in M_{I}^{\alpha }$
, we have
$m\in M_{I}^{\alpha }$
, we have
![]() $m_{\Omega }\in M_{I}^{\alpha }$
. Hence,
$m_{\Omega }\in M_{I}^{\alpha }$
. Hence,
![]() $m_{\Omega }\in M^{\alpha }_I\cap \bigoplus _{A\in \Omega }(M_I)_{A}^{\emptyset }$
. Namely,
$m_{\Omega }\in M^{\alpha }_I\cap \bigoplus _{A\in \Omega }(M_I)_{A}^{\emptyset }$
. Namely,
![]() $M_{I}$
satisfies (LE). Since
$M_{I}$
satisfies (LE). Since
![]() $M_{K}$
is a quotient of
$M_{K}$
is a quotient of
![]() $M_{I}$
, it also satisfies (LE).
$M_{I}$
, it also satisfies (LE).
2.3 Standard filtration
Note that
![]() $\{A\} = \{A'\in \mathcal {A}\mid A'\ge A\}\cap \{A'\in \mathcal {A}\mid A'\le A\}$
is locally closed. Let
$\{A\} = \{A'\in \mathcal {A}\mid A'\ge A\}\cap \{A'\in \mathcal {A}\mid A'\le A\}$
is locally closed. Let
![]() $S_{0}$
be a flat commutative graded S-algebra. We say that an object M of
$S_{0}$
be a flat commutative graded S-algebra. We say that an object M of
![]() $\widetilde {\mathcal {K}}(S_0)$
admits a standard filtration if
$\widetilde {\mathcal {K}}(S_0)$
admits a standard filtration if
![]() $M_{\{A\}}$
is a graded free
$M_{\{A\}}$
is a graded free
![]() $S_0$
-module for any
$S_0$
-module for any
![]() $A\in \mathcal {A}$
. Let
$A\in \mathcal {A}$
. Let
![]() $\widetilde {\mathcal {K}}_\Delta (S_0)$
be the full subcategory of
$\widetilde {\mathcal {K}}_\Delta (S_0)$
be the full subcategory of
![]() $\widetilde {\mathcal {K}}(S_0)$
consisting of an object M which admits a standard filtration and for which
$\widetilde {\mathcal {K}}(S_0)$
consisting of an object M which admits a standard filtration and for which
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite. By Lemma 2.12, if
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite. By Lemma 2.12, if
![]() $M\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
, then
$M\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
, then
![]() $M_{K}\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
for any locally closed subset
$M_{K}\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
for any locally closed subset
![]() $K\subset \mathcal {A}$
.
$K\subset \mathcal {A}$
.
Lemma 2.14. Let
![]() $M_1,\dots ,M_l\in \widetilde {\mathcal {K}}(S_0)$
and assume that
$M_1,\dots ,M_l\in \widetilde {\mathcal {K}}(S_0)$
and assume that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_1),\dots ,\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_l)$
are all finite. Let
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_1),\dots ,\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_l)$
are all finite. Let
![]() $I\subset \mathcal {A}$
be a closed subset and
$I\subset \mathcal {A}$
be a closed subset and
![]() $A\in I$
such that
$A\in I$
such that
![]() $I\setminus \{A\}$
is closed. Then, there exist closed subsets
$I\setminus \{A\}$
is closed. Then, there exist closed subsets
![]() $I_0\subset I_1\subset \dotsm \subset I_r$
and
$I_0\subset I_1\subset \dotsm \subset I_r$
and
![]() $k \in \{1,\dots ,r\}$
such that
$k \in \{1,\dots ,r\}$
such that
![]() $\#(I_j\setminus I_{j - 1}) = 1$
for any
$\#(I_j\setminus I_{j - 1}) = 1$
for any
![]() $j = 1,\dots ,r$
,
$j = 1,\dots ,r$
,
![]() $I_k\cap (\bigcup _i\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)) = I\cap (\bigcup _i\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i))$
,
$I_k\cap (\bigcup _i\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)) = I\cap (\bigcup _i\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i))$
,
![]() $I_{k - 1} = I_k\setminus \{A\}$
,
$I_{k - 1} = I_k\setminus \{A\}$
,
![]() $(M_i)_{I_0} = 0$
and
$(M_i)_{I_0} = 0$
and
![]() $(M_i)_{I_r} = M$
for any
$(M_i)_{I_r} = M$
for any
![]() $i =1,\dots ,l$
. In particular, we have
$i =1,\dots ,l$
. In particular, we have
![]() $(M_i)_I\simeq (M_i)_{I_k}$
for all
$(M_i)_I\simeq (M_i)_{I_k}$
for all
![]() $i = 1,\dots ,l$
.
$i = 1,\dots ,l$
.
Proof. There exist
![]() $A_0^-,A_0^+$
such that
$A_0^-,A_0^+$
such that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)\subset [A_0^-,A_0^+]$
for any
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)\subset [A_0^-,A_0^+]$
for any
![]() $i = 1,\dots ,l$
by [Reference LusztigLus80, Proposition 3.7]. Put
$i = 1,\dots ,l$
by [Reference LusztigLus80, Proposition 3.7]. Put
![]() $I_0 = \{A'\in \mathcal {A}\mid A'\nless A_0^+\}\cap I$
. We enumerate the elements in
$I_0 = \{A'\in \mathcal {A}\mid A'\nless A_0^+\}\cap I$
. We enumerate the elements in
![]() $(I\setminus \{A\})\cap [A_0^-,A_0^+]$
(resp.
$(I\setminus \{A\})\cap [A_0^-,A_0^+]$
(resp.
![]() $[A_0^-,A_0^+]\setminus I$
) as
$[A_0^-,A_0^+]\setminus I$
) as
![]() $\{A_1,\dots ,A_{k - 1}\}$
(resp.
$\{A_1,\dots ,A_{k - 1}\}$
(resp.
![]() $\{A_{k + 1},\dots ,A_r\}$
) such that
$\{A_{k + 1},\dots ,A_r\}$
) such that
![]() $A_i\ge A_j$
implies
$A_i\ge A_j$
implies
![]() $i\le j$
. Put
$i\le j$
. Put
![]() $A_k = A$
. Then, it is easy to see that
$A_k = A$
. Then, it is easy to see that
![]() $I_i = I_0\cup \{A_1,\dots ,A_i\}$
is closed and satisfies the conditions of the lemma.
$I_i = I_0\cup \{A_1,\dots ,A_i\}$
is closed and satisfies the conditions of the lemma.
Lemma 2.15. Let
![]() $M\in \widetilde {\mathcal {K}}_\Delta (S_0)$
, and let K be a locally closed subset. Then
$M\in \widetilde {\mathcal {K}}_\Delta (S_0)$
, and let K be a locally closed subset. Then
![]() $M_K$
is graded free as a left
$M_K$
is graded free as a left
![]() $S_0$
-module.
$S_0$
-module.
Proof. Since
![]() $M_K\in \widetilde {\mathcal {K}}_\Delta (S_0)$
, we may assume
$M_K\in \widetilde {\mathcal {K}}_\Delta (S_0)$
, we may assume
![]() $K = \mathcal {A}$
. Take closed subsets
$K = \mathcal {A}$
. Take closed subsets
![]() $I_0\subset I_1\subset \dotsm \subset I_r$
such that
$I_0\subset I_1\subset \dotsm \subset I_r$
such that
![]() $I_{i + 1}\setminus I_i = \{A_i\}$
,
$I_{i + 1}\setminus I_i = \{A_i\}$
,
![]() $M_{I_0} = 0$
and
$M_{I_0} = 0$
and
![]() $M_{I_r} = M$
. Then,
$M_{I_r} = M$
. Then,
![]() $M_{I_{i + 1}}/M_{I_{i}} = M_{\{A_i\}}$
is a graded free
$M_{I_{i + 1}}/M_{I_{i}} = M_{\{A_i\}}$
is a graded free
![]() $S_0$
-module. Hence,
$S_0$
-module. Hence,
![]() $M_{I_r}/M_{I_0} = M$
is also graded free.
$M_{I_r}/M_{I_0} = M$
is also graded free.
Finally, we define the category
![]() $\widetilde {\mathcal {K}}_P(S_0)$
, which plays an important role later. The definitions are taken from [Reference Fiebig and LaniniFL15, Lemma 4.11].
$\widetilde {\mathcal {K}}_P(S_0)$
, which plays an important role later. The definitions are taken from [Reference Fiebig and LaniniFL15, Lemma 4.11].
Definition 2.16. We say that a sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\widetilde {\mathcal {K}}_{\Delta }(S_0)$
satisfies (ES) if the composition
$\widetilde {\mathcal {K}}_{\Delta }(S_0)$
satisfies (ES) if the composition
![]() $M_1\to M_2\to M_3$
is zero and
$M_1\to M_2\to M_3$
is zero and
is exact for any
![]() $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
We define the category
![]() $\widetilde {\mathcal {K}}_P(S_0)\subset \widetilde {\mathcal {K}}_{\Delta }(S_0)$
as follows:
$\widetilde {\mathcal {K}}_P(S_0)\subset \widetilde {\mathcal {K}}_{\Delta }(S_0)$
as follows:
![]() $M\in \widetilde {\mathcal {K}}_P(S_0)$
if and only if for any sequence
$M\in \widetilde {\mathcal {K}}_P(S_0)$
if and only if for any sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\widetilde {\mathcal {K}}_{\Delta }(S_0)$
which satisfies (ES), the induced sequence
$\widetilde {\mathcal {K}}_{\Delta }(S_0)$
which satisfies (ES), the induced sequence
is exact.
Lemma 2.17. Assume that
![]() $M_1,M_2,M_3\in \widetilde {\mathcal {K}}(S_0)$
satisfy
$M_1,M_2,M_3\in \widetilde {\mathcal {K}}(S_0)$
satisfy
![]() $\#\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i) < \infty $
(
$\#\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i) < \infty $
(
![]() $i = 1,2,3$
), and the sequence
$i = 1,2,3$
), and the sequence
![]() $M_1\to M_2\to M_3$
satisfies (ES). Then,
$M_1\to M_2\to M_3$
satisfies (ES). Then,
![]() $0\to (M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}\to 0$
is exact for any locally closed subset K.
$0\to (M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}\to 0$
is exact for any locally closed subset K.
Proof. Replacing
![]() $M_i$
with
$M_i$
with
![]() $(M_i)_K$
for
$(M_i)_K$
for
![]() $i = 1,2,3$
, we may assume
$i = 1,2,3$
, we may assume
![]() $K = \mathcal {A}$
. We can take closed subsets
$K = \mathcal {A}$
. We can take closed subsets
![]() $I_0\subset I_1\subset \dotsb \subset I_r$
such that
$I_0\subset I_1\subset \dotsb \subset I_r$
such that
![]() $(M_i)_{I_0} = 0$
,
$(M_i)_{I_0} = 0$
,
![]() $(M_i)_{I_r} = M_i$
and
$(M_i)_{I_r} = M_i$
and
![]() $\#(I_{j + 1}\setminus I_j) = 1$
for
$\#(I_{j + 1}\setminus I_j) = 1$
for
![]() $i = 1,2,3$
and
$i = 1,2,3$
and
![]() $j = 0,\dots ,r$
, as in Lemma 2.14. Then, the exactness of
$j = 0,\dots ,r$
, as in Lemma 2.14. Then, the exactness of
![]() $0\to (M_1)_{I_j}\to (M_2)_{I_j}\to (M_3)_{I_j}\to 0$
follows by induction on j and a standard diagram argument.
$0\to (M_1)_{I_j}\to (M_2)_{I_j}\to (M_3)_{I_j}\to 0$
follows by induction on j and a standard diagram argument.
Lemma 2.18. Let
![]() $M\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
, and
$M\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
, and
![]() $I_1\supset I_2$
are closed subsets of
$I_1\supset I_2$
are closed subsets of
![]() $\mathcal {A}$
. Then,
$\mathcal {A}$
. Then,
![]() $M_{I_2}\to M_{I_1}\to M_{I_1}/M_{I_2}$
satisfies (ES).
$M_{I_2}\to M_{I_1}\to M_{I_1}/M_{I_2}$
satisfies (ES).
Proof. Note that
![]() $M_{I_1}/M_{I_2} = M_{I_1\setminus I_2}$
. The lemma follows from Lemma 2.12.
$M_{I_1}/M_{I_2} = M_{I_1\setminus I_2}$
. The lemma follows from Lemma 2.12.
We put
![]() $\widetilde {\mathcal {K}}' = \widetilde {\mathcal {K}}'(S)$
,
$\widetilde {\mathcal {K}}' = \widetilde {\mathcal {K}}'(S)$
,
![]() $\widetilde {\mathcal {K}} = \widetilde {\mathcal {K}}(S)$
,
$\widetilde {\mathcal {K}} = \widetilde {\mathcal {K}}(S)$
,
![]() $\widetilde {\mathcal {K}}_{\Delta } = \widetilde {\mathcal {K}}_{\Delta }(S)$
and
$\widetilde {\mathcal {K}}_{\Delta } = \widetilde {\mathcal {K}}_{\Delta }(S)$
and
![]() $\widetilde {\mathcal {K}}_P = \widetilde {\mathcal {K}}_P(S)$
. We also put
$\widetilde {\mathcal {K}}_P = \widetilde {\mathcal {K}}_P(S)$
. We also put
![]() $(\widetilde {\mathcal {K}}')^* = \widetilde {\mathcal {K}}'(S^*)$
,
$(\widetilde {\mathcal {K}}')^* = \widetilde {\mathcal {K}}'(S^*)$
,
![]() $\widetilde {\mathcal {K}}^* = \widetilde {\mathcal {K}}(S^*)$
,
$\widetilde {\mathcal {K}}^* = \widetilde {\mathcal {K}}(S^*)$
,
![]() $\widetilde {\mathcal {K}}^*_{\Delta } = \widetilde {\mathcal {K}}_{\Delta }(S^*)$
and
$\widetilde {\mathcal {K}}^*_{\Delta } = \widetilde {\mathcal {K}}_{\Delta }(S^*)$
and
![]() $\widetilde {\mathcal {K}}^*_P = \widetilde {\mathcal {K}}_P(S^*)$
for
$\widetilde {\mathcal {K}}^*_P = \widetilde {\mathcal {K}}_P(S^*)$
for
![]() $*\in \Delta \cup \{\emptyset \}$
.
$*\in \Delta \cup \{\emptyset \}$
.
2.4 Hecke action
For
![]() $\lambda \in \Lambda _{{\mathbb {K}}}$
and
$\lambda \in \Lambda _{{\mathbb {K}}}$
and
![]() $f\in \Lambda _{{\mathbb {K}}}^{\vee }$
, we put
$f\in \Lambda _{{\mathbb {K}}}^{\vee }$
, we put
![]() $\langle \lambda ,f\rangle = f_{A}(\lambda _{A})$
for
$\langle \lambda ,f\rangle = f_{A}(\lambda _{A})$
for
![]() $A\in \mathcal {A}$
. It is easy to see that this does not depend on A and gives an isomorphism
$A\in \mathcal {A}$
. It is easy to see that this does not depend on A and gives an isomorphism
![]() $\Lambda _{{\mathbb {K}}}^{\vee }\simeq \operatorname {\mathrm {Hom}}_{{\mathbb {K}}}(\Lambda _{{\mathbb {K}}},{\mathbb {K}})$
. Let
$\Lambda _{{\mathbb {K}}}^{\vee }\simeq \operatorname {\mathrm {Hom}}_{{\mathbb {K}}}(\Lambda _{{\mathbb {K}}},{\mathbb {K}})$
. Let
![]() $s\in S_{{\mathrm {aff}}}$
, and we define
$s\in S_{{\mathrm {aff}}}$
, and we define
![]() $\alpha _s\in \Lambda _{{\mathbb {K}}}$
and
$\alpha _s\in \Lambda _{{\mathbb {K}}}$
and
![]() $\alpha _s^\vee \in \Lambda ^{\vee }_{{\mathbb {K}}}$
as follows: let
$\alpha _s^\vee \in \Lambda ^{\vee }_{{\mathbb {K}}}$
as follows: let
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $\alpha \in \Delta ^+$
such that
$\alpha \in \Delta ^+$
such that
![]() $s_{\alpha ,n} = As$
for some
$s_{\alpha ,n} = As$
for some
![]() $n\in {\mathbb {Z}}$
. Then, we put
$n\in {\mathbb {Z}}$
. Then, we put
![]() $\alpha _s = \alpha ^A$
and
$\alpha _s = \alpha ^A$
and
![]() $\alpha _s^\vee = (\alpha ^\vee )^A$
. These depend on a choice of A and
$\alpha _s^\vee = (\alpha ^\vee )^A$
. These depend on a choice of A and
![]() $\alpha $
. For each
$\alpha $
. For each
![]() $s\in S_{{\mathrm {aff}}}$
, we fix such A and
$s\in S_{{\mathrm {aff}}}$
, we fix such A and
![]() $\alpha $
and define
$\alpha $
and define
![]() $\alpha _s,\alpha _s^\vee $
.
$\alpha _s,\alpha _s^\vee $
.
Lemma 2.19. The pair
![]() $(\alpha _s,\alpha _s^\vee )$
does not depend on
$(\alpha _s,\alpha _s^\vee )$
does not depend on
![]() $A,\alpha $
up to sign.
$A,\alpha $
up to sign.
Proof. Let
![]() $A'\in \mathcal {A}$
and take
$A'\in \mathcal {A}$
and take
![]() $\beta \in \Delta ^+$
and
$\beta \in \Delta ^+$
and
![]() $m\in {\mathbb {Z}}$
such that
$m\in {\mathbb {Z}}$
such that
![]() $A's = s_{\beta ,m}A'$
. Take
$A's = s_{\beta ,m}A'$
. Take
![]() $x\in W^{\prime }_{\mathrm {aff}}$
such that
$x\in W^{\prime }_{\mathrm {aff}}$
such that
![]() $A' = xA$
. Then,
$A' = xA$
. Then,
![]() $A's = xAs = xs_{\alpha ,n}A$
. Since the action of
$A's = xAs = xs_{\alpha ,n}A$
. Since the action of
![]() $W^{\prime }_{{\mathrm {aff}}}$
on
$W^{\prime }_{{\mathrm {aff}}}$
on
![]() $X_{{\mathbb {R}}}$
preserves the set
$X_{{\mathbb {R}}}$
preserves the set
![]() $\{\{\lambda \in X_{{\mathbb {R}}}\mid \langle \lambda ,\alpha ^{\vee }\rangle = n\}\mid \alpha \in \Delta ,n\in {\mathbb {Z}}\}$
, there exists
$\{\{\lambda \in X_{{\mathbb {R}}}\mid \langle \lambda ,\alpha ^{\vee }\rangle = n\}\mid \alpha \in \Delta ,n\in {\mathbb {Z}}\}$
, there exists
![]() $(\gamma ,k)\in \Delta \times {\mathbb {Z}}$
such that
$(\gamma ,k)\in \Delta \times {\mathbb {Z}}$
such that
![]() $xs_{\alpha ,n} = s_{\gamma ,k}x$
. Moreover,
$xs_{\alpha ,n} = s_{\gamma ,k}x$
. Moreover,
![]() $\gamma \in \{\pm \overline {x}(\alpha )\}$
, where
$\gamma \in \{\pm \overline {x}(\alpha )\}$
, where
![]() $\overline {x}\in W_{\mathrm {f}}$
is the image of x under
$\overline {x}\in W_{\mathrm {f}}$
is the image of x under
![]() $W^{\prime }_{{\mathrm {aff}}}\to W_{\mathrm {f}}$
. We may assume
$W^{\prime }_{{\mathrm {aff}}}\to W_{\mathrm {f}}$
. We may assume
![]() $\gamma = \overline {x}(\alpha )$
. We have
$\gamma = \overline {x}(\alpha )$
. We have
![]() $A's = s_{\gamma ,k}xA = s_{\gamma ,k}A'$
. Hence,
$A's = s_{\gamma ,k}xA = s_{\gamma ,k}A'$
. Hence,
![]() $s_{\gamma ,k} = s_{\beta ,m}$
and therefore,
$s_{\gamma ,k} = s_{\beta ,m}$
and therefore,
![]() $\beta = \varepsilon \gamma = \varepsilon \overline {x}(\alpha )$
for
$\beta = \varepsilon \gamma = \varepsilon \overline {x}(\alpha )$
for
![]() $\varepsilon = 1$
or
$\varepsilon = 1$
or
![]() $\varepsilon = -1$
. We have
$\varepsilon = -1$
. We have
![]() $\beta ^{A'} = \varepsilon \overline {x}(\alpha )^{xA} = \varepsilon \alpha ^A$
and
$\beta ^{A'} = \varepsilon \overline {x}(\alpha )^{xA} = \varepsilon \alpha ^A$
and
![]() $(\beta ^\vee )^{A'} = \varepsilon (\alpha ^\vee )^{A}$
.
$(\beta ^\vee )^{A'} = \varepsilon (\alpha ^\vee )^{A}$
.
We have that
![]() $(\Lambda _{{\mathbb {K}}},\{\alpha _s\}_{s\in S_{{\mathrm {aff}}}},\{\alpha _s^\vee \}_{s\in S_{{\mathrm {aff}}}})$
is a realization which satisfies Demazure surjectivity [Reference Elias and WilliamsonEW16, Definition 3.1]. Let
$(\Lambda _{{\mathbb {K}}},\{\alpha _s\}_{s\in S_{{\mathrm {aff}}}},\{\alpha _s^\vee \}_{s\in S_{{\mathrm {aff}}}})$
is a realization which satisfies Demazure surjectivity [Reference Elias and WilliamsonEW16, Definition 3.1]. Let
![]() ${\mathcal {S}\mathrm {Bimod}}$
be the category introduced in [Reference AbeAbe21]. We remark that [Reference AbeAbe21, Assumption 3.2] is satisfied in this case by [Reference AbeAbe20a, Theorem 1.2, Proposition 3.7]. Set
${\mathcal {S}\mathrm {Bimod}}$
be the category introduced in [Reference AbeAbe21]. We remark that [Reference AbeAbe21, Assumption 3.2] is satisfied in this case by [Reference AbeAbe20a, Theorem 1.2, Proposition 3.7]. Set
![]() $R^{\emptyset } = R[((\alpha ^\vee )^A)^{-1}\mid \alpha \in \Delta ]$
for
$R^{\emptyset } = R[((\alpha ^\vee )^A)^{-1}\mid \alpha \in \Delta ]$
for
![]() $A\in \mathcal {A}$
. It is easy to see that this does not depend on A. We put
$A\in \mathcal {A}$
. It is easy to see that this does not depend on A. We put
![]() $B^{\emptyset } = R^{\emptyset }\otimes _{R}B$
for
$B^{\emptyset } = R^{\emptyset }\otimes _{R}B$
for
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
.
$B\in {\mathcal {S}\mathrm {Bimod}}$
.
Recall that we have an object
![]() $B_s\in {\mathcal {S}\mathrm {Bimod}}$
. Set
$B_s\in {\mathcal {S}\mathrm {Bimod}}$
. Set
![]() $R^s = \{f\in R\mid s(f) = f\}$
. As an R-bimodule,
$R^s = \{f\in R\mid s(f) = f\}$
. As an R-bimodule,
![]() $B_s = R\otimes _{R^s}R(1)\simeq \{(f,g)\in R^2\mid f\equiv g\pmod {\alpha _s}\}$
and we have the decomposition of
$B_s = R\otimes _{R^s}R(1)\simeq \{(f,g)\in R^2\mid f\equiv g\pmod {\alpha _s}\}$
and we have the decomposition of
![]() $B_s^{\emptyset } = \bigoplus _{w\in W}(B_s)^{\emptyset }_{w}$
, where
$B_s^{\emptyset } = \bigoplus _{w\in W}(B_s)^{\emptyset }_{w}$
, where
 $$ \begin{align*} (B_s)^{\emptyset}_e & = R^{\emptyset}(\delta_s\otimes 1 - 1\otimes s(\delta_s)),\\ (B_s)^{\emptyset}_s & = R^{\emptyset}(\delta_s\otimes 1 - 1\otimes \delta_s),\\ (B_s)^{\emptyset}_w & = 0\quad (w\ne e,s). \end{align*} $$
$$ \begin{align*} (B_s)^{\emptyset}_e & = R^{\emptyset}(\delta_s\otimes 1 - 1\otimes s(\delta_s)),\\ (B_s)^{\emptyset}_s & = R^{\emptyset}(\delta_s\otimes 1 - 1\otimes \delta_s),\\ (B_s)^{\emptyset}_w & = 0\quad (w\ne e,s). \end{align*} $$
Here,
![]() $\delta _s\in \Lambda ^\vee _{{\mathbb {K}}}$
is chosen such that
$\delta _s\in \Lambda ^\vee _{{\mathbb {K}}}$
is chosen such that
![]() $\langle \alpha _s,\delta _s\rangle = 1$
. The decomposition does not depend on our choice of
$\langle \alpha _s,\delta _s\rangle = 1$
. The decomposition does not depend on our choice of
![]() $\delta _s$
.
$\delta _s$
.
Lemma 2.20. Let
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
. Then, there exists a decomposition
$B\in {\mathcal {S}\mathrm {Bimod}}$
. Then, there exists a decomposition
![]() $B^{\emptyset } = \bigoplus _{x\in W_{\mathrm {aff}}}B_x^{\emptyset }$
such that
$B^{\emptyset } = \bigoplus _{x\in W_{\mathrm {aff}}}B_x^{\emptyset }$
such that
![]() $\operatorname {\mathrm {Frac}}(R)\otimes _{R^\emptyset }B_x^{\emptyset }\simeq B_x^{\operatorname {\mathrm {Frac}}(R)}$
. Here,
$\operatorname {\mathrm {Frac}}(R)\otimes _{R^\emptyset }B_x^{\emptyset }\simeq B_x^{\operatorname {\mathrm {Frac}}(R)}$
. Here,
![]() $B_x^{\operatorname {\mathrm {Frac}}(R)}$
is the
$B_x^{\operatorname {\mathrm {Frac}}(R)}$
is the
![]() $\operatorname {\mathrm {Frac}}(R)$
-bimodule as in the definition of
$\operatorname {\mathrm {Frac}}(R)$
-bimodule as in the definition of
![]() ${\mathcal {S}\mathrm {Bimod}}$
.
${\mathcal {S}\mathrm {Bimod}}$
.
Proof. Assume that
![]() $B_1\in {\mathcal {S}\mathrm {Bimod}}$
is a direct summand of
$B_1\in {\mathcal {S}\mathrm {Bimod}}$
is a direct summand of
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
, and let
$B\in {\mathcal {S}\mathrm {Bimod}}$
, and let
![]() $e\in \operatorname {\mathrm {End}}_{{\mathcal {S}\mathrm {Bimod}}}(B)$
be the idempotent such that
$e\in \operatorname {\mathrm {End}}_{{\mathcal {S}\mathrm {Bimod}}}(B)$
be the idempotent such that
![]() $B_1 = e(B)$
. If B satisfies the lemma, then by putting
$B_1 = e(B)$
. If B satisfies the lemma, then by putting
![]() $(B_1)_x^{\emptyset } = e(B_x^{\emptyset })$
, we see that
$(B_1)_x^{\emptyset } = e(B_x^{\emptyset })$
, we see that
![]() $B_1$
also satisfies the lemma. Therefore, we may assume
$B_1$
also satisfies the lemma. Therefore, we may assume
![]() $B = B_{s_1}\otimes \cdots \otimes B_{s_l}$
for
$B = B_{s_1}\otimes \cdots \otimes B_{s_l}$
for
![]() $s_i\in S_{{\mathrm {aff}}}$
. Note that for
$s_i\in S_{{\mathrm {aff}}}$
. Note that for
![]() $B = B_s$
, the lemma holds as we have seen in the above. Hence, it is sufficient to prove that if
$B = B_s$
, the lemma holds as we have seen in the above. Hence, it is sufficient to prove that if
![]() $B_1,B_2$
satisfy the lemma, then
$B_1,B_2$
satisfy the lemma, then
![]() $B = B_1\otimes B_2$
also satisfies the lemma.
$B = B_1\otimes B_2$
also satisfies the lemma.
For
![]() $x\in W_{{\mathrm {aff}}}$
and
$x\in W_{{\mathrm {aff}}}$
and
![]() $b\in (B_1)_x^{\emptyset }$
, we have
$b\in (B_1)_x^{\emptyset }$
, we have
![]() $bf = x(f)b$
for
$bf = x(f)b$
for
![]() $f\in R$
. Since
$f\in R$
. Since
![]() $\{(\alpha ^\vee )^{A}\mid \alpha \in \Delta \}$
is stable under the action of x, the formula says that
$\{(\alpha ^\vee )^{A}\mid \alpha \in \Delta \}$
is stable under the action of x, the formula says that
![]() $(B_1)_x^{\emptyset }$
is also a right
$(B_1)_x^{\emptyset }$
is also a right
![]() $R^{\emptyset }$
-module. Therefore,
$R^{\emptyset }$
-module. Therefore,
![]() $B_1^{\emptyset }$
is also a right
$B_1^{\emptyset }$
is also a right
![]() $R^{\emptyset }$
-module. Hence,
$R^{\emptyset }$
-module. Hence,
![]() $R^{\emptyset }\otimes _{R}B_1\otimes _{R}B_2\simeq B_1^{\emptyset }\otimes _{R}B_2\simeq B_1^{\emptyset }\otimes _{R^{\emptyset }}R^{\emptyset }\otimes _{R}B_2 \simeq B_1^{\emptyset }\otimes _{R^{\emptyset }}B_2^{\emptyset }$
. We put
$R^{\emptyset }\otimes _{R}B_1\otimes _{R}B_2\simeq B_1^{\emptyset }\otimes _{R}B_2\simeq B_1^{\emptyset }\otimes _{R^{\emptyset }}R^{\emptyset }\otimes _{R}B_2 \simeq B_1^{\emptyset }\otimes _{R^{\emptyset }}B_2^{\emptyset }$
. We put
![]() $B_{x}^{\emptyset } = \bigoplus _{yz = x}(B_1)_y^{\emptyset }\otimes _{R^{\emptyset }}(B_2)_z^{\emptyset }$
. Then, we get
$B_{x}^{\emptyset } = \bigoplus _{yz = x}(B_1)_y^{\emptyset }\otimes _{R^{\emptyset }}(B_2)_z^{\emptyset }$
. Then, we get
![]() $B^{\emptyset } = \bigoplus _{x\in W_{{\mathrm {aff}}}}B_x^{\emptyset }$
and we have
$B^{\emptyset } = \bigoplus _{x\in W_{{\mathrm {aff}}}}B_x^{\emptyset }$
and we have
![]() $\operatorname {\mathrm {Frac}}(R)\otimes _{R^{\emptyset }}B_x^{\emptyset }\simeq B_x^{\operatorname {\mathrm {Frac}}(R)}$
.
$\operatorname {\mathrm {Frac}}(R)\otimes _{R^{\emptyset }}B_x^{\emptyset }\simeq B_x^{\operatorname {\mathrm {Frac}}(R)}$
.
Let
![]() $S_{0}$
be a flat commutative graded S-algebra. For
$S_{0}$
be a flat commutative graded S-algebra. For
![]() $M\in \widetilde {\mathcal {K}}'(S_0)$
and
$M\in \widetilde {\mathcal {K}}'(S_0)$
and
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
, we define
$B\in {\mathcal {S}\mathrm {Bimod}}$
, we define
![]() $M*B\in \widetilde {\mathcal {K}}'(S_0)$
by
$M*B\in \widetilde {\mathcal {K}}'(S_0)$
by
-
• As an
 $(S_0,R)$
-bimodule,
$(S_0,R)$
-bimodule,
 $M*B = M\otimes _R B$
.
$M*B = M\otimes _R B$
. -
• We put
 $(M*B)_A^\emptyset = \bigoplus _{x\in W_{\mathrm {aff}}}M_{Ax^{-1}}^{\emptyset }\otimes _{R^\emptyset } B_x^{\emptyset }$
.
$(M*B)_A^\emptyset = \bigoplus _{x\in W_{\mathrm {aff}}}M_{Ax^{-1}}^{\emptyset }\otimes _{R^\emptyset } B_x^{\emptyset }$
.
Let
![]() $f\colon M\to N$
be a morphism in
$f\colon M\to N$
be a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
. We have
$\widetilde {\mathcal {K}}'(S_0)$
. We have
![]() $f(M_{Ax^{-1}}^{\emptyset })\subset \bigoplus _{A'\in Ax^{-1} + {\mathbb {Z}}\Delta ,A'\ge Ax^{-1}}N_{A'}^{\emptyset }$
. By Lemma 2.3, for
$f(M_{Ax^{-1}}^{\emptyset })\subset \bigoplus _{A'\in Ax^{-1} + {\mathbb {Z}}\Delta ,A'\ge Ax^{-1}}N_{A'}^{\emptyset }$
. By Lemma 2.3, for
![]() $A'\in Ax^{-1} + {\mathbb {Z}}\Delta $
,
$A'\in Ax^{-1} + {\mathbb {Z}}\Delta $
,
![]() $A'\ge Ax^{-1}$
if and only if
$A'\ge Ax^{-1}$
if and only if
![]() $A'x\ge A$
. Therefore,
$A'x\ge A$
. Therefore,
![]() $\bigoplus _{A'\in Ax^{-1} + {\mathbb {Z}}\Delta ,A'\ge Ax^{-1}}N_{A'}^{\emptyset } = \bigoplus _{A'\in A + {\mathbb {Z}}\Delta ,A'\ge A}N_{A'x^{-1}}^{\emptyset }$
by replacing
$\bigoplus _{A'\in Ax^{-1} + {\mathbb {Z}}\Delta ,A'\ge Ax^{-1}}N_{A'}^{\emptyset } = \bigoplus _{A'\in A + {\mathbb {Z}}\Delta ,A'\ge A}N_{A'x^{-1}}^{\emptyset }$
by replacing
![]() $A'x$
with
$A'x$
with
![]() $A'$
. Hence,
$A'$
. Hence,
Therefore,
![]() $(f\otimes \operatorname {\mathrm {id}})$
gives a morphism in
$(f\otimes \operatorname {\mathrm {id}})$
gives a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
. Similarly, if
$\widetilde {\mathcal {K}}'(S_0)$
. Similarly, if
![]() $f\colon B_1\to B_2$
is a morphism in
$f\colon B_1\to B_2$
is a morphism in
![]() ${\mathcal {S}\mathrm {Bimod}}$
, then
${\mathcal {S}\mathrm {Bimod}}$
, then
![]() $\operatorname {\mathrm {id}}\otimes f\colon M*B_1\to M*B_2$
is a morphism in
$\operatorname {\mathrm {id}}\otimes f\colon M*B_1\to M*B_2$
is a morphism in
![]() $\mathcal {K}'(S_0)$
.
$\mathcal {K}'(S_0)$
.
For each
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
,
$B\in {\mathcal {S}\mathrm {Bimod}}$
,
![]() $B_x^{\emptyset }$
is free as a left
$B_x^{\emptyset }$
is free as a left
![]() $R^{\emptyset }$
-module. We put
$R^{\emptyset }$
-module. We put
![]() $\operatorname {\mathrm {supp}}_{W_{{\mathrm {aff}}}}(B) = \{x\in W_{{\mathrm {aff}}}\mid B_{x}^{\emptyset }\ne 0\}$
. The following lemma follows.
$\operatorname {\mathrm {supp}}_{W_{{\mathrm {aff}}}}(B) = \{x\in W_{{\mathrm {aff}}}\mid B_{x}^{\emptyset }\ne 0\}$
. The following lemma follows.
Lemma 2.21. We have
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M*B) = \{Ax\mid A\in \operatorname {\mathrm {supp}}_{\mathcal {A}}(M),x\in \operatorname {\mathrm {supp}}_{W_{\mathrm {aff}}}(B)\}$
.
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M*B) = \{Ax\mid A\in \operatorname {\mathrm {supp}}_{\mathcal {A}}(M),x\in \operatorname {\mathrm {supp}}_{W_{\mathrm {aff}}}(B)\}$
.
Consider
![]() $M\otimes _R B_s = M\otimes _{R^s}R(1) = M(1)\otimes 1\oplus M(1)\otimes \delta _s$
. In
$M\otimes _R B_s = M\otimes _{R^s}R(1) = M(1)\otimes 1\oplus M(1)\otimes \delta _s$
. In
![]() $(M\otimes _R B_s)^{\emptyset } = M^{\emptyset }(1)\otimes 1\oplus M^{\emptyset }(1)\otimes \delta _s$
, we have
$(M\otimes _R B_s)^{\emptyset } = M^{\emptyset }(1)\otimes 1\oplus M^{\emptyset }(1)\otimes \delta _s$
, we have
 $$ \begin{align} \begin{aligned} (M*B_s)^{\emptyset}_A & = \{m\delta_s\otimes 1 - m\otimes s(\delta_s)\mid m\in M_{A}^{\emptyset}\}\oplus \{m\delta_s\otimes 1 - m\otimes \delta_s\mid m\in M_{As}^{\emptyset}\}\\ & \simeq M_{A}^{\emptyset}\oplus M_{As}^{\emptyset}. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} (M*B_s)^{\emptyset}_A & = \{m\delta_s\otimes 1 - m\otimes s(\delta_s)\mid m\in M_{A}^{\emptyset}\}\oplus \{m\delta_s\otimes 1 - m\otimes \delta_s\mid m\in M_{As}^{\emptyset}\}\\ & \simeq M_{A}^{\emptyset}\oplus M_{As}^{\emptyset}. \end{aligned} \end{align} $$
The isomorphism is given by
![]() $m\otimes f\mapsto (mf,ms(f))$
. Note that the last isomorphism is an isomorphism as left
$m\otimes f\mapsto (mf,ms(f))$
. Note that the last isomorphism is an isomorphism as left
![]() $S_0^{\emptyset }$
-modules. As right R-modules, if
$S_0^{\emptyset }$
-modules. As right R-modules, if
![]() $m\in (M*B_s)^{\emptyset }_A$
corresponds to
$m\in (M*B_s)^{\emptyset }_A$
corresponds to
![]() $(m_1,m_2)\in M_{A}^{\emptyset }\oplus M_{As}^{\emptyset }$
, then
$(m_1,m_2)\in M_{A}^{\emptyset }\oplus M_{As}^{\emptyset }$
, then
![]() $mf$
corresponds to
$mf$
corresponds to
![]() $(m_1f,m_2s(f))$
.
$(m_1f,m_2s(f))$
.
Proposition 2.22. Let
![]() $M,N\in \widetilde {\mathcal {K}}'(S_0)$
. We have
$M,N\in \widetilde {\mathcal {K}}'(S_0)$
. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(M,N*B_s)\simeq \operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(M*B_s,N)$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(M,N*B_s)\simeq \operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(M*B_s,N)$
.
Proof. Take
![]() $\delta \in \Lambda ^\vee _{{\mathbb {K}}}$
such that
$\delta \in \Lambda ^\vee _{{\mathbb {K}}}$
such that
![]() $\langle \alpha _s,\delta \rangle = 1$
. As
$\langle \alpha _s,\delta \rangle = 1$
. As
![]() $(S_0,R)$
-bimodules, we have
$(S_0,R)$
-bimodules, we have
![]() $N*B_s = N\otimes _{R^s}R(1)$
and
$N*B_s = N\otimes _{R^s}R(1)$
and
![]() $M*B_s = M\otimes _{R^s}R(1)$
. For
$M*B_s = M\otimes _{R^s}R(1)$
. For
![]() $\varphi \colon M\otimes _{R^s}R(1)\to N$
, define
$\varphi \colon M\otimes _{R^s}R(1)\to N$
, define
![]() $\psi \colon M\to N\otimes _{R^s}R(1)$
by
$\psi \colon M\to N\otimes _{R^s}R(1)$
by
![]() $\psi (m) = \varphi (m\delta \otimes 1)\otimes 1 - \varphi (m\otimes 1)\otimes s(\delta )$
. We know that if
$\psi (m) = \varphi (m\delta \otimes 1)\otimes 1 - \varphi (m\otimes 1)\otimes s(\delta )$
. We know that if
![]() $\varphi $
is an
$\varphi $
is an
![]() $(S_0,R)$
-bimodule homomorphism,
$(S_0,R)$
-bimodule homomorphism,
![]() $\psi $
is also an
$\psi $
is also an
![]() $(S_0,R)$
-bimodule homomorphism and it induces a bijection between the spaces of
$(S_0,R)$
-bimodule homomorphism and it induces a bijection between the spaces of
![]() $(S_0,R)$
-bimodule homomorphisms (ee, for example, [Reference LibedinskyLib08, Lemma 3.3]). We prove that
$(S_0,R)$
-bimodule homomorphisms (ee, for example, [Reference LibedinskyLib08, Lemma 3.3]). We prove that
![]() $\varphi $
is a morphism in
$\varphi $
is a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
if and only if
$\widetilde {\mathcal {K}}'(S_0)$
if and only if
![]() $\psi $
is a morphism in
$\psi $
is a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
.
$\widetilde {\mathcal {K}}'(S_0)$
.
Set
![]() $a(m) = m\delta \otimes 1 - m\otimes s(\delta )$
and
$a(m) = m\delta \otimes 1 - m\otimes s(\delta )$
and
![]() $b(m) = ms(\delta ) \otimes 1 - m\otimes s(\delta )$
for
$b(m) = ms(\delta ) \otimes 1 - m\otimes s(\delta )$
for
![]() $m\in M^\emptyset $
. We also define
$m\in M^\emptyset $
. We also define
![]() $a'(n),b'(n)\in N^{\emptyset }\otimes _{R^s}R$
for
$a'(n),b'(n)\in N^{\emptyset }\otimes _{R^s}R$
for
![]() $n\in N^\emptyset $
in the same way. Then, we have
$n\in N^\emptyset $
in the same way. Then, we have
![]() $(M*B_s)_{A}^{\emptyset } = a(M_{A}^{\emptyset }) + b(M_{As}^{\emptyset })$
and the same for N by (2.1) for
$(M*B_s)_{A}^{\emptyset } = a(M_{A}^{\emptyset }) + b(M_{As}^{\emptyset })$
and the same for N by (2.1) for
![]() $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
Let
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $m\in M_{A}^{\emptyset }$
. By the definition,
$m\in M_{A}^{\emptyset }$
. By the definition,
![]() $\psi (m) = \varphi (a(m))\otimes 1 + b'(\varphi (m\otimes 1))$
. Since
$\psi (m) = \varphi (a(m))\otimes 1 + b'(\varphi (m\otimes 1))$
. Since
![]() $a(m)\in (M*B_s)^{\emptyset }_A$
,
$a(m)\in (M*B_s)^{\emptyset }_A$
,
![]() $\varphi (a(m))\otimes 1 = (\alpha _s)_{A}^{-1}\varphi (a(m))\alpha _s\otimes 1 = (\alpha _s)_{A}^{-1}a'(\varphi (a(m))) - (\alpha _s)_{A}^{-1}b'(\varphi (a(m)))$
. However, we have
$\varphi (a(m))\otimes 1 = (\alpha _s)_{A}^{-1}\varphi (a(m))\alpha _s\otimes 1 = (\alpha _s)_{A}^{-1}a'(\varphi (a(m))) - (\alpha _s)_{A}^{-1}b'(\varphi (a(m)))$
. However, we have
![]() $m\otimes 1 = (\alpha _s)_{A}^{-1}m\alpha _s\otimes 1 = (\alpha _s)_{A}^{-1}a(m) - (\alpha _s)_{A}^{-1}b(m)$
. Since
$m\otimes 1 = (\alpha _s)_{A}^{-1}m\alpha _s\otimes 1 = (\alpha _s)_{A}^{-1}a(m) - (\alpha _s)_{A}^{-1}b(m)$
. Since
![]() $\varphi $
and
$\varphi $
and
![]() $b'$
are left
$b'$
are left
![]() $S_0$
-equivariant, we get
$S_0$
-equivariant, we get
![]() $\psi (m) = (\alpha _s)_{A}^{-1}a'(\varphi (a(m))) - (\alpha _s)_{A}^{-1}b'(\varphi (b(m)))$
.
$\psi (m) = (\alpha _s)_{A}^{-1}a'(\varphi (a(m))) - (\alpha _s)_{A}^{-1}b'(\varphi (b(m)))$
.
Assume that
![]() $\varphi $
is a morphism in
$\varphi $
is a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
. Then, for any
$\widetilde {\mathcal {K}}'(S_0)$
. Then, for any
![]() $m\in M_{A}^{\emptyset }$
,
$m\in M_{A}^{\emptyset }$
,
![]() $\varphi (a(m))\in \bigoplus _{A'\ge A}N_{A'}^{\emptyset }$
. Hence,
$\varphi (a(m))\in \bigoplus _{A'\ge A}N_{A'}^{\emptyset }$
. Hence,
![]() $a'(\varphi (a(m)))\in \bigoplus _{A' \ge A}(N*B_s)_{A'}^{\emptyset }$
. Since
$a'(\varphi (a(m)))\in \bigoplus _{A' \ge A}(N*B_s)_{A'}^{\emptyset }$
. Since
![]() $b(m)\in (M*B_s)_{As}^{\emptyset }$
, we have
$b(m)\in (M*B_s)_{As}^{\emptyset }$
, we have
![]() $\varphi (b(m))\in \bigoplus _{A' \ge As, A'\in As + {\mathbb {Z}}\Delta }N_{A'}^{\emptyset }$
. Therefore,
$\varphi (b(m))\in \bigoplus _{A' \ge As, A'\in As + {\mathbb {Z}}\Delta }N_{A'}^{\emptyset }$
. Therefore,
![]() $b'(\varphi (b(m)))\in \bigoplus _{A' \ge As,A' \in As + {\mathbb {Z}}\Delta }(N*B_s)_{A's}^{\emptyset }$
. If
$b'(\varphi (b(m)))\in \bigoplus _{A' \ge As,A' \in As + {\mathbb {Z}}\Delta }(N*B_s)_{A's}^{\emptyset }$
. If
![]() $A'\in As + {\mathbb {Z}}\Delta $
satisfies
$A'\in As + {\mathbb {Z}}\Delta $
satisfies
![]() $A'\ge As$
, since
$A'\ge As$
, since
![]() $s\colon As + {\mathbb {Z}}\Delta \to A + {\mathbb {Z}}\Delta $
preserves the order, we get
$s\colon As + {\mathbb {Z}}\Delta \to A + {\mathbb {Z}}\Delta $
preserves the order, we get
![]() $A's \ge A$
. Hence,
$A's \ge A$
. Hence,
![]() $b'(\varphi (b(m)))\in \bigoplus _{A' \ge A}(N*B_s)_{A'}^{\emptyset }$
. Therefore,
$b'(\varphi (b(m)))\in \bigoplus _{A' \ge A}(N*B_s)_{A'}^{\emptyset }$
. Therefore,
![]() $\psi $
is a morphism in
$\psi $
is a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
.
$\widetilde {\mathcal {K}}'(S_0)$
.
However, assume that
![]() $\psi $
is a morphism in
$\psi $
is a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
. Consider the map
$\widetilde {\mathcal {K}}'(S_0)$
. Consider the map
![]() $\Phi \colon N\otimes _{R^s}R\to N$
defined by
$\Phi \colon N\otimes _{R^s}R\to N$
defined by
![]() $n\otimes f\mapsto nf$
. Then,
$n\otimes f\mapsto nf$
. Then,
![]() $\Phi (a'(n)) = n\alpha _s$
and
$\Phi (a'(n)) = n\alpha _s$
and
![]() $\Phi (b'(n)) = 0$
. Therefore,
$\Phi (b'(n)) = 0$
. Therefore,
![]() $\Phi ((N*B_s)_{A}^{\emptyset }) = \Phi (a'(N_{A}^{\emptyset }) + b'(N_{As}^{\emptyset }))\subset N_{A}^{\emptyset }$
. Let
$\Phi ((N*B_s)_{A}^{\emptyset }) = \Phi (a'(N_{A}^{\emptyset }) + b'(N_{As}^{\emptyset }))\subset N_{A}^{\emptyset }$
. Let
![]() $m\in M_{A}^{\emptyset }$
. Then applying
$m\in M_{A}^{\emptyset }$
. Then applying
![]() $\Phi $
to
$\Phi $
to
![]() $\psi (m) = (\alpha _s)_{A}^{-1}a'(\varphi (a(m))) - (\alpha _s)_{A}^{-1}b'(\varphi (b(m)))$
, we get
$\psi (m) = (\alpha _s)_{A}^{-1}a'(\varphi (a(m))) - (\alpha _s)_{A}^{-1}b'(\varphi (b(m)))$
, we get
![]() $(\alpha _s)_{A}^{-1}\varphi (a(m))\alpha _s\in \bigoplus _{A'\in A + {\mathbb {Z}}\Delta ,A'\ge A}M_{A'}^{\emptyset }$
. Hence,
$(\alpha _s)_{A}^{-1}\varphi (a(m))\alpha _s\in \bigoplus _{A'\in A + {\mathbb {Z}}\Delta ,A'\ge A}M_{A'}^{\emptyset }$
. Hence,
![]() $\varphi (a(M_{A}^{\emptyset }))\subset \bigoplus _{A'\ge A}N_{A'}^{\emptyset }$
. Similarly, using
$\varphi (a(M_{A}^{\emptyset }))\subset \bigoplus _{A'\ge A}N_{A'}^{\emptyset }$
. Similarly, using
![]() $N\otimes _{R^s}R\to N$
defined by
$N\otimes _{R^s}R\to N$
defined by
![]() $n\otimes f\mapsto ns(f)$
, we get
$n\otimes f\mapsto ns(f)$
, we get
![]() $\varphi (b(M_{As}^{\emptyset }))\subset \bigoplus _{A'\ge A}N_{A'}^{\emptyset }$
. Since
$\varphi (b(M_{As}^{\emptyset }))\subset \bigoplus _{A'\ge A}N_{A'}^{\emptyset }$
. Since
![]() $(M*B_s)_{A}^{\emptyset } = a(M_{A}^{\emptyset }) + b(M_{As}^{\emptyset })$
,
$(M*B_s)_{A}^{\emptyset } = a(M_{A}^{\emptyset }) + b(M_{As}^{\emptyset })$
,
![]() $\varphi $
is a morphism in
$\varphi $
is a morphism in
![]() $\widetilde {\mathcal {K}}'(S_0)$
.
$\widetilde {\mathcal {K}}'(S_0)$
.
Lemma 2.23. Let
![]() $M\in \widetilde {\mathcal {K}}'(S_0)$
.
$M\in \widetilde {\mathcal {K}}'(S_0)$
.
-
(1) For
 $\alpha \in \Delta $
,
$\alpha \in \Delta $
,
 $s\in S_{{\mathrm {aff}}}$
and
$s\in S_{{\mathrm {aff}}}$
and
 $\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
, set
$\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}$
, set
 $M^{(\Omega )} = M^{\alpha }\cap \bigoplus _{A\in \Omega }M_A^{\emptyset }$
. Then, we have the following.
$M^{(\Omega )} = M^{\alpha }\cap \bigoplus _{A\in \Omega }M_A^{\emptyset }$
. Then, we have the following.-
(a) If
 $\Omega s = \Omega $
, then
$\Omega s = \Omega $
, then
 $(M*B_s)^{(\Omega )} \simeq M^{(\Omega )}*B_s$
.
$(M*B_s)^{(\Omega )} \simeq M^{(\Omega )}*B_s$
. -
(b) If
 $\Omega s \ne \Omega $
, then the right action of
$\Omega s \ne \Omega $
, then the right action of
 $\alpha _s$
on
$\alpha _s$
on
 $M^{(\Omega )}$
is invertible and we have
$M^{(\Omega )}$
is invertible and we have  $$\begin{align*}(M*B_s)^{(\Omega)}\simeq M^{(\Omega)}\otimes(\delta_s\otimes 1 - 1\otimes s(\delta_s))\oplus M^{(\Omega s)}\otimes(\delta_s\otimes 1 - 1\otimes \delta_s) \end{align*}$$
$$\begin{align*}(M*B_s)^{(\Omega)}\simeq M^{(\Omega)}\otimes(\delta_s\otimes 1 - 1\otimes s(\delta_s))\oplus M^{(\Omega s)}\otimes(\delta_s\otimes 1 - 1\otimes \delta_s) \end{align*}$$
where
 $\langle \alpha _s,\delta _s\rangle = 1$
.
$\langle \alpha _s,\delta _s\rangle = 1$
.
-
-
(2) If
 $M\in \widetilde {\mathcal {K}}'(S_0)$
satisfies (LE), then
$M\in \widetilde {\mathcal {K}}'(S_0)$
satisfies (LE), then
 $M*B$
also satisfies (LE) for any
$M*B$
also satisfies (LE) for any
 $B\in {\mathcal {S}\mathrm {Bimod}}$
.
$B\in {\mathcal {S}\mathrm {Bimod}}$
.
Proof. We have
 $$ \begin{align*} (M*B_s)^{(\Omega)} & = M^{\alpha}*B_s\cap \bigoplus_{A\in \Omega}(M*B_s)_{A}^{\emptyset}\\ & = M^{\alpha}*B_s\cap \left(\bigoplus_{A\in \Omega}M_A^{\emptyset}\otimes (B_s)^{\emptyset}_e\oplus \bigoplus_{A\in \Omega}M_{As}^{\emptyset}\otimes (B_s)^{\emptyset}_s\right). \end{align*} $$
$$ \begin{align*} (M*B_s)^{(\Omega)} & = M^{\alpha}*B_s\cap \bigoplus_{A\in \Omega}(M*B_s)_{A}^{\emptyset}\\ & = M^{\alpha}*B_s\cap \left(\bigoplus_{A\in \Omega}M_A^{\emptyset}\otimes (B_s)^{\emptyset}_e\oplus \bigoplus_{A\in \Omega}M_{As}^{\emptyset}\otimes (B_s)^{\emptyset}_s\right). \end{align*} $$
If
![]() $\Omega s = \Omega $
, then in the second direct sum, we can replace
$\Omega s = \Omega $
, then in the second direct sum, we can replace
![]() $As$
with A. Therefore,
$As$
with A. Therefore,
 $$ \begin{align*} (M*B_s)^{(\Omega)} & = M^{\alpha}*B_s\cap \left(\bigoplus_{A\in \Omega}M_A^{\emptyset}\otimes (B_s)^{\emptyset}_e\oplus \bigoplus_{A\in \Omega}M_{A}^{\emptyset}\otimes (B_s)^{\emptyset}_s\right)\\ & = M^{\alpha}*B_s\cap \bigoplus_{A\in \Omega}M_A^{\emptyset}\otimes (B_s)^{\emptyset}\\ & = (M^{\alpha}\cap \bigoplus_{A\in \Omega}M_A^{\emptyset})\otimes B_s\\ & = M^{(\Omega)}* B_s. \end{align*} $$
$$ \begin{align*} (M*B_s)^{(\Omega)} & = M^{\alpha}*B_s\cap \left(\bigoplus_{A\in \Omega}M_A^{\emptyset}\otimes (B_s)^{\emptyset}_e\oplus \bigoplus_{A\in \Omega}M_{A}^{\emptyset}\otimes (B_s)^{\emptyset}_s\right)\\ & = M^{\alpha}*B_s\cap \bigoplus_{A\in \Omega}M_A^{\emptyset}\otimes (B_s)^{\emptyset}\\ & = (M^{\alpha}\cap \bigoplus_{A\in \Omega}M_A^{\emptyset})\otimes B_s\\ & = M^{(\Omega)}* B_s. \end{align*} $$
Assume that
![]() $\Omega s\ne \Omega $
and take
$\Omega s\ne \Omega $
and take
![]() $A\in \Omega $
. Set
$A\in \Omega $
. Set
![]() $\beta ^\vee = (\alpha _s^\vee )_A$
. Then the assumption
$\beta ^\vee = (\alpha _s^\vee )_A$
. Then the assumption
![]() $\Omega s\ne \Omega $
tells us that
$\Omega s\ne \Omega $
tells us that
![]() $\beta ^\vee \ne \pm \alpha ^\vee $
. Hence,
$\beta ^\vee \ne \pm \alpha ^\vee $
. Hence,
![]() $\beta ^\vee $
is invertible in
$\beta ^\vee $
is invertible in
![]() $S^\alpha $
. The element
$S^\alpha $
. The element
![]() $s_\alpha (\beta ^\vee )$
is also invertible.
$s_\alpha (\beta ^\vee )$
is also invertible.
Let
![]() $\delta \in X^\vee _{{\mathbb {K}}}$
such that
$\delta \in X^\vee _{{\mathbb {K}}}$
such that
![]() $\langle \alpha ,\delta \rangle = 1$
. For
$\langle \alpha ,\delta \rangle = 1$
. For
![]() $m \in M^{(\Omega )}$
, there exists
$m \in M^{(\Omega )}$
, there exists
![]() $m_1\in \bigoplus _{A'\in A + {\mathbb {Z}} \alpha }M_{A'}^{\emptyset }$
and
$m_1\in \bigoplus _{A'\in A + {\mathbb {Z}} \alpha }M_{A'}^{\emptyset }$
and
![]() $m_2\in \bigoplus _{A'\in s_{(\alpha ,0)}A + {\mathbb {Z}} \alpha }M_{A'}^{\emptyset }$
such that
$m_2\in \bigoplus _{A'\in s_{(\alpha ,0)}A + {\mathbb {Z}} \alpha }M_{A'}^{\emptyset }$
such that
![]() $m = m_1 + m_2$
. For each
$m = m_1 + m_2$
. For each
![]() $f\in R$
,
$f\in R$
,
![]() $m_1f = f_Am_1$
and
$m_1f = f_Am_1$
and
![]() $m_2f = s_\alpha (f_A)m_2$
. By calculations using this, we have
$m_2f = s_\alpha (f_A)m_2$
. By calculations using this, we have
 $$\begin{align*}\left(\frac{1}{\beta^\vee}m + \frac{\langle\alpha,\beta^\vee\rangle}{\beta s_{\alpha}(\beta^\vee)}(\delta m - m\delta^A)\right)\alpha_s^\vee = m. \end{align*}$$
$$\begin{align*}\left(\frac{1}{\beta^\vee}m + \frac{\langle\alpha,\beta^\vee\rangle}{\beta s_{\alpha}(\beta^\vee)}(\delta m - m\delta^A)\right)\alpha_s^\vee = m. \end{align*}$$
Hence, the right action of
![]() $\alpha _s^\vee $
is invertible.
$\alpha _s^\vee $
is invertible.
Therefore, we have
![]() $(M*B_s)^{(\Omega )} = (M*B_s[\alpha _s^{-1}])^{(\Omega )}$
where
$(M*B_s)^{(\Omega )} = (M*B_s[\alpha _s^{-1}])^{(\Omega )}$
where
![]() $B_s[(\alpha _s^\vee )^{-1}] = B_s\otimes _{R}R[(\alpha _s^\vee )^{-1}]$
. Since
$B_s[(\alpha _s^\vee )^{-1}] = B_s\otimes _{R}R[(\alpha _s^\vee )^{-1}]$
. Since
![]() $B_s[(\alpha _s^\vee )^{-1}] = R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes s(\delta _s))\oplus R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes \delta _s)$
with
$B_s[(\alpha _s^\vee )^{-1}] = R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes s(\delta _s))\oplus R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes \delta _s)$
with
![]() $R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes s(\delta _s))\subset (B_s)_e^{\emptyset }$
and
$R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes s(\delta _s))\subset (B_s)_e^{\emptyset }$
and
![]() $R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes \delta _s)\subset (B_s)_s^{\emptyset }$
, the definition of
$R[(\alpha _s^\vee )^{-1}](\delta _s\otimes 1 - 1\otimes \delta _s)\subset (B_s)_s^{\emptyset }$
, the definition of
![]() $(M*B_s)^{(\Omega )}$
implies (b).
$(M*B_s)^{(\Omega )}$
implies (b).
(2) Fix
![]() $\alpha \in \Delta $
. By replacing
$\alpha \in \Delta $
. By replacing
![]() $M^{\alpha }$
with an object which is isomorphic to
$M^{\alpha }$
with an object which is isomorphic to
![]() $M^{\alpha }$
, we may assume
$M^{\alpha }$
, we may assume
![]() $M^{\alpha } = \bigoplus _{\Omega \in W_{\alpha ,{\mathrm {aff}}}'\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }M_A^{\emptyset }\cap M^{\alpha })$
. Let
$M^{\alpha } = \bigoplus _{\Omega \in W_{\alpha ,{\mathrm {aff}}}'\backslash \mathcal {A}}(\bigoplus _{A\in \Omega }M_A^{\emptyset }\cap M^{\alpha })$
. Let
![]() $\{\Omega _i\}$
be a complete set of representatives for
$\{\Omega _i\}$
be a complete set of representatives for
![]() $\{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}\mid \Omega s\ne \Omega \}/\{e,s\}$
. Then, we have
$\{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}\mid \Omega s\ne \Omega \}/\{e,s\}$
. Then, we have
 $$ \begin{align*} \bigoplus_{\Omega\in W^{\prime}_{\alpha,{\mathrm{aff}}}\backslash \mathcal{A}}(M^{\alpha}*B_s)^{(\Omega)} & = \bigoplus_{\Omega s = \Omega}(M*B_s)^{(\Omega)} \oplus \bigoplus_{i}((M*B_s)^{(\Omega_i)}\oplus (M*B_s)^{(\Omega_i s)})\\ & = \bigoplus_{\Omega s = \Omega}M^{(\Omega)}*B_s \oplus \bigoplus_{i}((M*B_s)^{(\Omega_i)}\oplus (M*B_s)^{(\Omega_i s)}). \end{align*} $$
$$ \begin{align*} \bigoplus_{\Omega\in W^{\prime}_{\alpha,{\mathrm{aff}}}\backslash \mathcal{A}}(M^{\alpha}*B_s)^{(\Omega)} & = \bigoplus_{\Omega s = \Omega}(M*B_s)^{(\Omega)} \oplus \bigoplus_{i}((M*B_s)^{(\Omega_i)}\oplus (M*B_s)^{(\Omega_i s)})\\ & = \bigoplus_{\Omega s = \Omega}M^{(\Omega)}*B_s \oplus \bigoplus_{i}((M*B_s)^{(\Omega_i)}\oplus (M*B_s)^{(\Omega_i s)}). \end{align*} $$
From the argument of the proof of (1)(b), we have
![]() $M^{(\Omega _i)}\otimes (\delta _s \otimes 1 - 1\otimes s(\delta _s))\oplus M^{(\Omega _i)}\otimes (\delta _s\otimes 1 - 1\otimes \delta _s) = M^{(\Omega _i)}\otimes B_s[\alpha _s^{-1}] = M^{(\Omega _i)}\otimes B_s$
. Therefore, by (1)(b),
$M^{(\Omega _i)}\otimes (\delta _s \otimes 1 - 1\otimes s(\delta _s))\oplus M^{(\Omega _i)}\otimes (\delta _s\otimes 1 - 1\otimes \delta _s) = M^{(\Omega _i)}\otimes B_s[\alpha _s^{-1}] = M^{(\Omega _i)}\otimes B_s$
. Therefore, by (1)(b),
![]() $((M*B_s)^{(\Omega _i)}\oplus (M*B_s)^{(\Omega _i s)}) = M^{(\Omega _i)}\otimes B_s\oplus M^{(\Omega _i s)}\otimes B_s$
. Hence,
$((M*B_s)^{(\Omega _i)}\oplus (M*B_s)^{(\Omega _i s)}) = M^{(\Omega _i)}\otimes B_s\oplus M^{(\Omega _i s)}\otimes B_s$
. Hence,
 $$ \begin{align*} \bigoplus_{\Omega\in W^{\prime}_{\alpha,{\mathrm{aff}}}\backslash \mathcal{A}}(M*B_s)^{(\Omega)} & = \bigoplus_{\Omega s = \Omega}M^{(\Omega)}*B_s \oplus \bigoplus_{i}(M^{(\Omega_i )}*B_s\oplus M^{(\Omega_i s)}*B_s)\\ & = \bigoplus_{\Omega\in W^{\prime}_{\alpha,{\mathrm{aff}}}\backslash \mathcal{A}}M^{(\Omega)}*B_s\\ & = M^{\alpha}*B_s. \end{align*} $$
$$ \begin{align*} \bigoplus_{\Omega\in W^{\prime}_{\alpha,{\mathrm{aff}}}\backslash \mathcal{A}}(M*B_s)^{(\Omega)} & = \bigoplus_{\Omega s = \Omega}M^{(\Omega)}*B_s \oplus \bigoplus_{i}(M^{(\Omega_i )}*B_s\oplus M^{(\Omega_i s)}*B_s)\\ & = \bigoplus_{\Omega\in W^{\prime}_{\alpha,{\mathrm{aff}}}\backslash \mathcal{A}}M^{(\Omega)}*B_s\\ & = M^{\alpha}*B_s. \end{align*} $$
Hence,
![]() $M*B_s$
satisfies (LE).
$M*B_s$
satisfies (LE).
2.5 An example
We give an example of our category. Let
![]() $(X = {\mathbb {Z}},\Delta = \{\alpha = 2\},X^\vee = {\mathbb {Z}},\Delta ^\vee = \{\alpha ^\vee = 1\})$
be the root system of type
$(X = {\mathbb {Z}},\Delta = \{\alpha = 2\},X^\vee = {\mathbb {Z}},\Delta ^\vee = \{\alpha ^\vee = 1\})$
be the root system of type
![]() $A_1$
. The Weyl group
$A_1$
. The Weyl group
![]() $W_{\mathrm {f}}$
is
$W_{\mathrm {f}}$
is
![]() $\{e,s_{\alpha }\}$
. Let
$\{e,s_{\alpha }\}$
. Let
![]() $s_1\in S_{{\mathrm {aff}}}$
(resp.
$s_1\in S_{{\mathrm {aff}}}$
(resp.
![]() $s_0\in S_{{\mathrm {aff}}}$
) be the element corresponding to
$s_0\in S_{{\mathrm {aff}}}$
) be the element corresponding to
![]() $W^{\prime }_{{\mathrm {aff}}}\{0\}$
(resp.
$W^{\prime }_{{\mathrm {aff}}}\{0\}$
(resp.
![]() $W^{\prime }_{{\mathrm {aff}}}\{1\}$
). Then,
$W^{\prime }_{{\mathrm {aff}}}\{1\}$
). Then,
![]() $S_{{\mathrm {aff}}} = \{s_0,s_1\}$
. The set of alcoves is given by
$S_{{\mathrm {aff}}} = \{s_0,s_1\}$
. The set of alcoves is given by
![]() $\mathcal {A} = \{A_n = \{r\in {\mathbb {R}} = X\otimes _{{\mathbb {Z}}}{\mathbb {R}}\mid n < r < n + 1\}\mid n\in {\mathbb {Z}}\}$
. We have
$\mathcal {A} = \{A_n = \{r\in {\mathbb {R}} = X\otimes _{{\mathbb {Z}}}{\mathbb {R}}\mid n < r < n + 1\}\mid n\in {\mathbb {Z}}\}$
. We have
![]() $A_ns_1 = A_{n - 1}$
if n is even and
$A_ns_1 = A_{n - 1}$
if n is even and
![]() $A_ns_1 = A_{n + 1}$
if n is odd. The algebra
$A_ns_1 = A_{n + 1}$
if n is odd. The algebra
![]() $S = \operatorname {\mathrm {Sym}}(X_{{\mathbb {K}}}^\vee )$
is isomorphic to the polynomial ring
$S = \operatorname {\mathrm {Sym}}(X_{{\mathbb {K}}}^\vee )$
is isomorphic to the polynomial ring
![]() ${\mathbb {K}}[\alpha ^\vee ]$
.
${\mathbb {K}}[\alpha ^\vee ]$
.
Define
![]() $Q_{A_n}\in \widetilde {\mathcal {K}}' = \widetilde {\mathcal {K}}'(S)$
as follows. As an
$Q_{A_n}\in \widetilde {\mathcal {K}}' = \widetilde {\mathcal {K}}'(S)$
as follows. As an
![]() $(S,R)$
-bimodule, we define
$(S,R)$
-bimodule, we define
![]() $Q_{A_n} = \{(f,g)\in S^2\mid f\equiv g\pmod {\alpha ^\vee }\}$
. Here, S acts naturally and
$Q_{A_n} = \{(f,g)\in S^2\mid f\equiv g\pmod {\alpha ^\vee }\}$
. Here, S acts naturally and
![]() $r\in R$
acts by
$r\in R$
acts by
![]() $(f,g)r = (r_{A_n}f,r_{A_{n + 1}}g)$
. We put
$(f,g)r = (r_{A_n}f,r_{A_{n + 1}}g)$
. We put
![]() $(Q_{A_n}^{\emptyset })_{A_n} = S^{\emptyset }\oplus 0$
,
$(Q_{A_n}^{\emptyset })_{A_n} = S^{\emptyset }\oplus 0$
,
![]() $(Q_{A_n}^{\emptyset })_{A_{n + 1}} = 0\oplus S^{\emptyset }$
and
$(Q_{A_n}^{\emptyset })_{A_{n + 1}} = 0\oplus S^{\emptyset }$
and
![]() $(Q_{A_n}^{\emptyset })_{A_m} = 0$
for
$(Q_{A_n}^{\emptyset })_{A_m} = 0$
for
![]() $m\ne n,n + 1$
(we denote this object
$m\ne n,n + 1$
(we denote this object
![]() $Q_{A_n,\alpha }$
later in 3.5).
$Q_{A_n,\alpha }$
later in 3.5).
We have
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_n}) = \{A_n,A_{n + 1}\}$
. We prove
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_n}) = \{A_n,A_{n + 1}\}$
. We prove
![]() $Q_{A_0}*B_{s_1} \simeq Q_{A_{-1}}\oplus Q_{A_{1}}$
. We have
$Q_{A_0}*B_{s_1} \simeq Q_{A_{-1}}\oplus Q_{A_{1}}$
. We have
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_0}*B_{s_1}) = \{A_0,A_{1},A_0s_1,A_{1}s_1\} = \{A_{- 1},A_{0},A_{1},A_{2}\}$
.
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_0}*B_{s_1}) = \{A_0,A_{1},A_0s_1,A_{1}s_1\} = \{A_{- 1},A_{0},A_{1},A_{2}\}$
.
Below, by an isomorphism
![]() $f\mapsto f_{A_0}$
, we identify
$f\mapsto f_{A_0}$
, we identify
![]() $R\simeq S = {\mathbb {K}}[\alpha ^\vee ]$
. Hence,
$R\simeq S = {\mathbb {K}}[\alpha ^\vee ]$
. Hence,
![]() $Q_{A_n} = \{(a,b)\in {\mathbb {K}}[\alpha ^\vee ]^2\mid a\equiv b\pmod {\alpha ^\vee }\}$
. Put
$Q_{A_n} = \{(a,b)\in {\mathbb {K}}[\alpha ^\vee ]^2\mid a\equiv b\pmod {\alpha ^\vee }\}$
. Put
![]() $s = s_{\alpha }$
which acts on
$s = s_{\alpha }$
which acts on
![]() ${\mathbb {K}}[\alpha ^\vee ]$
. The right actions of
${\mathbb {K}}[\alpha ^\vee ]$
. The right actions of
![]() $R\simeq {\mathbb {K}}[\alpha ^\vee ]$
on
$R\simeq {\mathbb {K}}[\alpha ^\vee ]$
on
![]() $Q_{A_0},Q_{A_1},Q_{A_{-1}}$
are given as follows: for
$Q_{A_0},Q_{A_1},Q_{A_{-1}}$
are given as follows: for
![]() $(a,b)\in Q_{A_0}$
, we have
$(a,b)\in Q_{A_0}$
, we have
![]() $(a,b)f = (af,bs(f))$
and for
$(a,b)f = (af,bs(f))$
and for
![]() $(c,d)\in Q_{A_1},Q_{A_{-1}}$
, we have
$(c,d)\in Q_{A_1},Q_{A_{-1}}$
, we have
![]() $(c,d)f = (cs(f),df)$
.
$(c,d)f = (cs(f),df)$
.
We have
![]() $B_{s_1}\simeq \{(f,g)\in {\mathbb {K}}[\alpha ^\vee ]\mid f \equiv g\pmod {\alpha ^\vee }\}$
,
$B_{s_1}\simeq \{(f,g)\in {\mathbb {K}}[\alpha ^\vee ]\mid f \equiv g\pmod {\alpha ^\vee }\}$
,
![]() $(B_{s_1}^{\emptyset })_{e} = {\mathbb {K}}[\alpha ^\vee ]^{\emptyset } \oplus 0$
and
$(B_{s_1}^{\emptyset })_{e} = {\mathbb {K}}[\alpha ^\vee ]^{\emptyset } \oplus 0$
and
![]() $(B_{s_1}^{\emptyset })_{s_1} = 0\oplus {\mathbb {K}}[\alpha ^\vee ]^{\emptyset }$
where
$(B_{s_1}^{\emptyset })_{s_1} = 0\oplus {\mathbb {K}}[\alpha ^\vee ]^{\emptyset }$
where
![]() ${\mathbb {K}}[\alpha ^\vee ]^{\emptyset } = {\mathbb {K}}[(\alpha ^\vee )^{\pm 1}]$
. We have
${\mathbb {K}}[\alpha ^\vee ]^{\emptyset } = {\mathbb {K}}[(\alpha ^\vee )^{\pm 1}]$
. We have
 $$ \begin{align*} & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{-1}} = ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0)\otimes (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset}), \\ & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{0}} = ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0)\otimes ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0),\\ & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{1}} = (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset})\otimes ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0), \\ & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{2}} = (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset})\otimes (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset}). \end{align*} $$
$$ \begin{align*} & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{-1}} = ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0)\otimes (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset}), \\ & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{0}} = ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0)\otimes ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0),\\ & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{1}} = (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset})\otimes ({\mathbb{K}}[\alpha^\vee]^{\emptyset}\oplus 0), \\ & (Q_{A_0}*B_{s_1})^{\emptyset}_{A_{2}} = (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset})\otimes (0\oplus {\mathbb{K}}[\alpha^\vee]^{\emptyset}). \end{align*} $$
These correspond to
![]() $A_{-1} = A_{0}s_{1}$
,
$A_{-1} = A_{0}s_{1}$
,
![]() $A_{0} = A_{0}e$
,
$A_{0} = A_{0}e$
,
![]() $A_{1} = A_{1}e$
and
$A_{1} = A_{1}e$
and
![]() $A_{2} = A_{1}s_1$
, respectively.
$A_{2} = A_{1}s_1$
, respectively.
We define
![]() $p_1\colon Q_{A_0}*B_s\to Q_{A_{- 1}}$
by
$p_1\colon Q_{A_0}*B_s\to Q_{A_{- 1}}$
by
![]() $p_1((a,b)\otimes (f,g)) = (ag,af)$
and
$p_1((a,b)\otimes (f,g)) = (ag,af)$
and
![]() $p_2\colon Q_{A_0}*B_s\to Q_{A_{1}}$
by
$p_2\colon Q_{A_0}*B_s\to Q_{A_{1}}$
by
![]() $p_2((a,b)\otimes (f,g)) = ((bs(f) - ag)/\alpha ^\vee ,(bs(g) - af)/\alpha ^\vee )$
. In the definition of
$p_2((a,b)\otimes (f,g)) = ((bs(f) - ag)/\alpha ^\vee ,(bs(g) - af)/\alpha ^\vee )$
. In the definition of
![]() $p_2$
, we note that
$p_2$
, we note that
![]() $bs(f)\equiv ag,bs(g)\equiv af\pmod {\alpha ^\vee }$
since
$bs(f)\equiv ag,bs(g)\equiv af\pmod {\alpha ^\vee }$
since
![]() $a\equiv b,s(f)\equiv f,s(g)\equiv g,f\equiv g\pmod {\alpha ^\vee }$
. These are
$a\equiv b,s(f)\equiv f,s(g)\equiv g,f\equiv g\pmod {\alpha ^\vee }$
. These are
![]() ${\mathbb {K}}[\alpha ^\vee ]$
-bimodule homomorphisms, and from the above description,
${\mathbb {K}}[\alpha ^\vee ]$
-bimodule homomorphisms, and from the above description,
![]() $p_1$
is a morphism in
$p_1$
is a morphism in
![]() $\widetilde {\mathcal {K}}'$
. We have
$\widetilde {\mathcal {K}}'$
. We have
![]() $p_2((1,0)\otimes (0,1)) = (-1/\alpha ^\vee ,0)$
. Hence,
$p_2((1,0)\otimes (0,1)) = (-1/\alpha ^\vee ,0)$
. Hence,
![]() $p_2((Q_{A_0}*B_{s_1})_{A_{-1}}^{\emptyset })\subset (Q_{A_{1}})_{A_1}^{\emptyset }$
. We also have
$p_2((Q_{A_0}*B_{s_1})_{A_{-1}}^{\emptyset })\subset (Q_{A_{1}})_{A_1}^{\emptyset }$
. We also have
![]() $p_2((Q_{A_0}*B_{s_1})^{\emptyset }_{A_1})\subset (Q_{A_{1}})_{A_1}^{\emptyset }$
,
$p_2((Q_{A_0}*B_{s_1})^{\emptyset }_{A_1})\subset (Q_{A_{1}})_{A_1}^{\emptyset }$
,
![]() $p_2((Q_{A_0}*B_{s_1})^{\emptyset }_{A_0}),p_2((Q_{A_0}*B_{s_1})^{\emptyset }_{A_2})\subset (Q_{A_{1}})_{A_2}^{\emptyset }$
. Therefore,
$p_2((Q_{A_0}*B_{s_1})^{\emptyset }_{A_0}),p_2((Q_{A_0}*B_{s_1})^{\emptyset }_{A_2})\subset (Q_{A_{1}})_{A_2}^{\emptyset }$
. Therefore,
![]() $p_2$
is also a morphism in
$p_2$
is also a morphism in
![]() $\widetilde {\mathcal {K}}'$
.
$\widetilde {\mathcal {K}}'$
.
We define
![]() $i_1\colon Q_{A_{- 1}}\to Q_{A_0}*B_{s_1}$
by
$i_1\colon Q_{A_{- 1}}\to Q_{A_0}*B_{s_1}$
by
![]() $i_1(a,b) = (b,a)\otimes (1,1) + ((a - b)/\alpha ^\vee ,(a - b)/\alpha ^\vee )\otimes (0,\alpha ^\vee )$
. In
$i_1(a,b) = (b,a)\otimes (1,1) + ((a - b)/\alpha ^\vee ,(a - b)/\alpha ^\vee )\otimes (0,\alpha ^\vee )$
. In
![]() $(Q_{A_0}*B_{s_1})^{\emptyset }$
,
$(Q_{A_0}*B_{s_1})^{\emptyset }$
,
![]() $i_1$
is given by
$i_1$
is given by
![]() $i_1(a,b) = (b,a)\otimes (1,0) + (a,b)\otimes (0,1)$
. It is easy to see that
$i_1(a,b) = (b,a)\otimes (1,0) + (a,b)\otimes (0,1)$
. It is easy to see that
![]() $i_1$
is a left
$i_1$
is a left
![]() ${\mathbb {K}}[\alpha ^\vee ]$
-module homomorphism. For
${\mathbb {K}}[\alpha ^\vee ]$
-module homomorphism. For
![]() $f\in {\mathbb {K}}[\alpha ^\vee ]$
, we have
$f\in {\mathbb {K}}[\alpha ^\vee ]$
, we have
![]() $i_1(a,b)f = (b,a)\otimes (f,0) + (a,b)\otimes (0,s(f)) = (b,a)f\otimes (1,0) + (a,b)s(f)\otimes (0,1) = (bf,as(f))\otimes (1,0) + (as(f),bf)\otimes (0,1) = i_1(as(f),bf) = i_1((a,b)f)$
. Therefore,
$i_1(a,b)f = (b,a)\otimes (f,0) + (a,b)\otimes (0,s(f)) = (b,a)f\otimes (1,0) + (a,b)s(f)\otimes (0,1) = (bf,as(f))\otimes (1,0) + (as(f),bf)\otimes (0,1) = i_1(as(f),bf) = i_1((a,b)f)$
. Therefore,
![]() $i_1$
is a
$i_1$
is a
![]() ${\mathbb {K}}[\alpha ^\vee ]$
-bimodule homomorphism. We can also check that
${\mathbb {K}}[\alpha ^\vee ]$
-bimodule homomorphism. We can also check that
![]() $i_1$
is a morphism in
$i_1$
is a morphism in
![]() $\widetilde {\mathcal {K}}'$
. We also define
$\widetilde {\mathcal {K}}'$
. We also define
![]() $i_2\colon Q_{A_1}\to Q_{A_0}*B_{s_1}$
by
$i_2\colon Q_{A_1}\to Q_{A_0}*B_{s_1}$
by
![]() $i_2(a,b) = (0,\alpha ^\vee )\otimes (s(a),s(b))$
. Then, it is straightforward to check that
$i_2(a,b) = (0,\alpha ^\vee )\otimes (s(a),s(b))$
. Then, it is straightforward to check that
![]() $i_2$
is a morphism in
$i_2$
is a morphism in
![]() $\widetilde {\mathcal {K}}'$
. Finally, straightforward calculations imply
$\widetilde {\mathcal {K}}'$
. Finally, straightforward calculations imply
![]() $p_1\circ i_1 = \operatorname {\mathrm {id}}$
,
$p_1\circ i_1 = \operatorname {\mathrm {id}}$
,
![]() $p_2 \circ i_2 = \operatorname {\mathrm {id}}$
,
$p_2 \circ i_2 = \operatorname {\mathrm {id}}$
,
![]() $i_1\circ p_1 + i_2\circ p_2 = \operatorname {\mathrm {id}}$
. Hence,
$i_1\circ p_1 + i_2\circ p_2 = \operatorname {\mathrm {id}}$
. Hence,
![]() $Q_{A_0}*B_{s_1}\simeq Q_{A_{-1}}\oplus Q_{A_1}$
.
$Q_{A_0}*B_{s_1}\simeq Q_{A_{-1}}\oplus Q_{A_1}$
.
Note that the decomposition
![]() $Q_{A_0}*B_{s_1} = \operatorname {\mathrm {Im}} i_1\oplus \operatorname {\mathrm {Im}} i_2$
is not compatible with respect to the decomposition over
$Q_{A_0}*B_{s_1} = \operatorname {\mathrm {Im}} i_1\oplus \operatorname {\mathrm {Im}} i_2$
is not compatible with respect to the decomposition over
![]() ${\mathbb {K}}[\alpha ^\vee ]^{\emptyset }$
since
${\mathbb {K}}[\alpha ^\vee ]^{\emptyset }$
since
![]() $i_1$
is not compatible with the decomposition.
$i_1$
is not compatible with the decomposition.
2.6 Hecke actions preserve
 $\widetilde {\mathcal {K}}_{\Delta }$
$\widetilde {\mathcal {K}}_{\Delta }$
We assume that
![]() ${\mathbb {K}}$
is local. Then, since any direct summand of a graded free S-module is also graded free, a direct summand of an object in
${\mathbb {K}}$
is local. Then, since any direct summand of a graded free S-module is also graded free, a direct summand of an object in
![]() $\widetilde {\mathcal {K}}_{\Delta }$
is also in
$\widetilde {\mathcal {K}}_{\Delta }$
is also in
![]() $\widetilde {\mathcal {K}}_{\Delta }$
. The aim of this subsection is to prove the following proposition.
$\widetilde {\mathcal {K}}_{\Delta }$
. The aim of this subsection is to prove the following proposition.
Proposition 2.24. We have
![]() $\widetilde {\mathcal {K}}_{\Delta } * {\mathcal {S}\mathrm {Bimod}}\subset \widetilde {\mathcal {K}}_{\Delta }$
.
$\widetilde {\mathcal {K}}_{\Delta } * {\mathcal {S}\mathrm {Bimod}}\subset \widetilde {\mathcal {K}}_{\Delta }$
.
We fix
![]() $M \in \widetilde {\mathcal {K}}_{\Delta }$
and
$M \in \widetilde {\mathcal {K}}_{\Delta }$
and
![]() $s\in S_{{\mathrm {aff}}}$
in this subsection and prove
$s\in S_{{\mathrm {aff}}}$
in this subsection and prove
![]() $M*B_s\in \widetilde {\mathcal {K}}_{\Delta }$
. The most difficult part is to prove that
$M*B_s\in \widetilde {\mathcal {K}}_{\Delta }$
. The most difficult part is to prove that
![]() $M*B_s$
satisfies (S). First we remark that, since
$M*B_s$
satisfies (S). First we remark that, since
![]() $M*B_s$
satisfies (LE) by Lemma 2.23,
$M*B_s$
satisfies (LE) by Lemma 2.23,
![]() $(M*B_s)^{\alpha }$
satisfies (S) by Lemma 2.10.
$(M*B_s)^{\alpha }$
satisfies (S) by Lemma 2.10.
Lemma 2.25. If I is a closed s-invariant subset of
![]() $\mathcal {A}$
, then
$\mathcal {A}$
, then
![]() $(M*B_s)_I\simeq M_I*B_s$
.
$(M*B_s)_I\simeq M_I*B_s$
.
Proof. We have
![]() $(M*B_s)_{I}^{\emptyset } = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes (B_s)_{e}^{\emptyset }\oplus \bigoplus _{A\in I}M_{As}^{\emptyset }\otimes (B_s)_{s}^{\emptyset }$
. Since I is s-invariant,
$(M*B_s)_{I}^{\emptyset } = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes (B_s)_{e}^{\emptyset }\oplus \bigoplus _{A\in I}M_{As}^{\emptyset }\otimes (B_s)_{s}^{\emptyset }$
. Since I is s-invariant,
![]() $\bigoplus _{A\in I}M_{As}^{\emptyset }\otimes (B_s)_{s}^{\emptyset } = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes (B_s)_s^{\emptyset }$
. Hence,
$\bigoplus _{A\in I}M_{As}^{\emptyset }\otimes (B_s)_{s}^{\emptyset } = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes (B_s)_s^{\emptyset }$
. Hence,
![]() $(M*B_s)_{I}^{\emptyset } = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes ((B_s)_{e}^{\emptyset }\oplus (B_s)_{s}^{\emptyset }) = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes B_{s}^{\emptyset } = M_I^{\emptyset }\otimes B_{s}^{\emptyset }$
.
$(M*B_s)_{I}^{\emptyset } = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes ((B_s)_{e}^{\emptyset }\oplus (B_s)_{s}^{\emptyset }) = \bigoplus _{A\in I}M_{A}^{\emptyset }\otimes B_{s}^{\emptyset } = M_I^{\emptyset }\otimes B_{s}^{\emptyset }$
.
Lemma 2.26. Let
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() $As < A$
and I (resp. J) be an s-invariant closed (resp. open) subset such that
$As < A$
and I (resp. J) be an s-invariant closed (resp. open) subset such that
![]() $I\cap J = \{A,As\}$
. Set
$I\cap J = \{A,As\}$
. Set
![]() $N = M*B_s$
. Then, we have
$N = M*B_s$
. Then, we have
as left S-modules.
Proof. First we note that
![]() $I\setminus \{A,As\} = I\setminus J$
and
$I\setminus \{A,As\} = I\setminus J$
and
![]() $I\setminus \{As\} = (I\setminus J)\cup \{A'\in \mathcal {A}\mid A'\ge A\}$
are closed. We have an exact sequence
$I\setminus \{As\} = (I\setminus J)\cup \{A'\in \mathcal {A}\mid A'\ge A\}$
are closed. We have an exact sequence
We have
![]() $(N_I/N_{I\setminus \{A,As\}})^{\emptyset } = N_{A}^{\emptyset }\oplus N_{As}^{\emptyset }$
and we have the following commutative diagram:
$(N_I/N_{I\setminus \{A,As\}})^{\emptyset } = N_{A}^{\emptyset }\oplus N_{As}^{\emptyset }$
and we have the following commutative diagram:

Therefore,
![]() $N_{I\setminus \{As\}}/N_{I\setminus \{A,As\}} = (N_I/N_{I\setminus \{A,As\}})\cap (N_A^{\emptyset }\oplus 0)$
.
$N_{I\setminus \{As\}}/N_{I\setminus \{A,As\}} = (N_I/N_{I\setminus \{A,As\}})\cap (N_A^{\emptyset }\oplus 0)$
.
Set
![]() $L = N_I/N_{I\setminus \{A,As\}}$
. By Lemma 2.25,
$L = N_I/N_{I\setminus \{A,As\}}$
. By Lemma 2.25,
![]() $L\simeq M_{\{A,As\}}\otimes _{R^s}R(1)$
. We have
$L\simeq M_{\{A,As\}}\otimes _{R^s}R(1)$
. We have
![]() $L^{\emptyset } = L_{A}^{\emptyset }\oplus L_{As}^{\emptyset }$
. We determine
$L^{\emptyset } = L_{A}^{\emptyset }\oplus L_{As}^{\emptyset }$
. We determine
![]() $L\cap (L_{A}^{\emptyset }\oplus 0)$
.
$L\cap (L_{A}^{\emptyset }\oplus 0)$
.
By (2.1), we have
![]() $L_{A}^{\emptyset }\simeq M_{A}^{\emptyset }\oplus M_ {As}^{\emptyset }$
and
$L_{A}^{\emptyset }\simeq M_{A}^{\emptyset }\oplus M_ {As}^{\emptyset }$
and
![]() $L_{As}^{\emptyset }\simeq M_{As}^{\emptyset }\oplus M_ {A}^{\emptyset }$
. In general, we write
$L_{As}^{\emptyset }\simeq M_{As}^{\emptyset }\oplus M_ {A}^{\emptyset }$
. In general, we write
![]() $m_{A'}$
for the image of
$m_{A'}$
for the image of
![]() $m\in M$
in
$m\in M$
in
![]() $M_{A'}^{\emptyset }$
, where
$M_{A'}^{\emptyset }$
, where
![]() $A'\in \mathcal {A}$
. The image of
$A'\in \mathcal {A}$
. The image of
![]() $m_1\otimes 1 + m_2\otimes \delta \in L = M_{\{A,As\}}\otimes _{R^s}R(1)$
in each direct summand is
$m_1\otimes 1 + m_2\otimes \delta \in L = M_{\{A,As\}}\otimes _{R^s}R(1)$
in each direct summand is
 $$ \begin{gather*} m_{1,A} + m_{2,A}\delta\in M_{A}^{\emptyset}\subset L_{A}^{\emptyset},\\ m_{1,As} + m_{2,As}s(\delta)\in M_{As}^{\emptyset}\subset L_{A}^{\emptyset},\\ m_{1,As} + m_{2,As}\delta\in M_{As}^{\emptyset}\subset L_{As}^{\emptyset},\\ m_{1,A} + m_{2,A}s(\delta)\in M_{A}^{\emptyset}\subset L_{As}^{\emptyset}. \end{gather*} $$
$$ \begin{gather*} m_{1,A} + m_{2,A}\delta\in M_{A}^{\emptyset}\subset L_{A}^{\emptyset},\\ m_{1,As} + m_{2,As}s(\delta)\in M_{As}^{\emptyset}\subset L_{A}^{\emptyset},\\ m_{1,As} + m_{2,As}\delta\in M_{As}^{\emptyset}\subset L_{As}^{\emptyset},\\ m_{1,A} + m_{2,A}s(\delta)\in M_{A}^{\emptyset}\subset L_{As}^{\emptyset}. \end{gather*} $$
Therefore,
![]() $m_1\otimes 1 + m_2\otimes \delta \in L_{A}^{\emptyset }$
if and only if
$m_1\otimes 1 + m_2\otimes \delta \in L_{A}^{\emptyset }$
if and only if
![]() $m_{1,As} + m_{2,As}\delta = 0$
,
$m_{1,As} + m_{2,As}\delta = 0$
,
![]() $m_{1,A} + m_{2,A}s(\delta ) = 0$
. Note that
$m_{1,A} + m_{2,A}s(\delta ) = 0$
. Note that
![]() $m_{2,As}\delta = (s(\delta ))_Am_{2,As}$
and
$m_{2,As}\delta = (s(\delta ))_Am_{2,As}$
and
![]() $m_{2,A}s(\delta ) = (s(\delta ))_{A}m_{2,A}$
. Therefore,
$m_{2,A}s(\delta ) = (s(\delta ))_{A}m_{2,A}$
. Therefore,
![]() $(m_1 + (s(\delta ))_Am_2)_{A'} = 0$
for
$(m_1 + (s(\delta ))_Am_2)_{A'} = 0$
for
![]() $A' = A,As$
. Hence,
$A' = A,As$
. Hence,
![]() $m_1 + (s(\delta ))_Am_2 = 0$
. Therefore, we have
$m_1 + (s(\delta ))_Am_2 = 0$
. Therefore, we have
which is isomorphic to
![]() $M_{\{A,As\}}(-1)$
.
$M_{\{A,As\}}(-1)$
.
The map
![]() $L\simeq M_{\{A,As\}}\otimes _{R^s}R(1)\ni m\otimes f\mapsto (s(f))_Am\in M_{\{A,As\}}(1)$
is surjective and, by the above argument, the kernel is
$L\simeq M_{\{A,As\}}\otimes _{R^s}R(1)\ni m\otimes f\mapsto (s(f))_Am\in M_{\{A,As\}}(1)$
is surjective and, by the above argument, the kernel is
![]() $L\cap (L_{A}^{\emptyset }\oplus 0)\simeq N_{I\setminus \{As\}}/N_{I\setminus \{A,As\}}$
. Therefore, by the exact sequence (2.2), we have
$L\cap (L_{A}^{\emptyset }\oplus 0)\simeq N_{I\setminus \{As\}}/N_{I\setminus \{A,As\}}$
. Therefore, by the exact sequence (2.2), we have
![]() $N_{I}/N_{I\setminus \{As\}}\simeq M_{\{A,As\}}(1)$
.
$N_{I}/N_{I\setminus \{As\}}\simeq M_{\{A,As\}}(1)$
.
Lemma 2.27. Let
![]() $A\in \mathcal {A}$
such that
$A\in \mathcal {A}$
such that
![]() $As < A$
, I is a closed subset and J is an open subset. Then, we have the following.
$As < A$
, I is a closed subset and J is an open subset. Then, we have the following.
-
(1) If
 $I\cap J = \{As\}$
, then
$I\cap J = \{As\}$
, then
 $(M*B_s)_I/(M*B_s)_{I\setminus J}\simeq M_{\{A,As\}}(1)$
as left S-modules.
$(M*B_s)_I/(M*B_s)_{I\setminus J}\simeq M_{\{A,As\}}(1)$
as left S-modules. -
(2) If
 $I\cap J = \{A\}$
, then
$I\cap J = \{A\}$
, then
 $(M*B_s)_I/(M*B_s)_{I\setminus J}\simeq M_{\{A,As\}}(-1)$
as left S-modules.
$(M*B_s)_I/(M*B_s)_{I\setminus J}\simeq M_{\{A,As\}}(-1)$
as left S-modules.
Proof. Set
![]() $N = M*B_s\in \widetilde {\mathcal {K}}'$
.
$N = M*B_s\in \widetilde {\mathcal {K}}'$
.
(1) Put
![]() $I_1 = \{A'\in \mathcal {A}\mid A'\ge As\}$
. This is s-invariant. Since I is closed and contains
$I_1 = \{A'\in \mathcal {A}\mid A'\ge As\}$
. This is s-invariant. Since I is closed and contains
![]() $As$
, we have
$As$
, we have
![]() $I_1\subset I$
. Hence,
$I_1\subset I$
. Hence,
![]() $N_{I_1}/N_{I_1\setminus \{As\}}\hookrightarrow N_{I}/N_{I\setminus \{As\}}$
. By Lemma 2.26, we have
$N_{I_1}/N_{I_1\setminus \{As\}}\hookrightarrow N_{I}/N_{I\setminus \{As\}}$
. By Lemma 2.26, we have
![]() $N_{I_1}/N_{I_1\setminus \{As\}}\simeq M_{\{A,As\}}(-1)$
. Hence, we have
$N_{I_1}/N_{I_1\setminus \{As\}}\simeq M_{\{A,As\}}(-1)$
. Hence, we have
![]() $M_{\{A,As\}}(-1)\hookrightarrow N_{I}/N_{I\setminus \{As\}}$
.
$M_{\{A,As\}}(-1)\hookrightarrow N_{I}/N_{I\setminus \{As\}}$
.
Let
![]() $\nu \in X^\vee _{{\mathbb {K}}}$
and write
$\nu \in X^\vee _{{\mathbb {K}}}$
and write
![]() $S_{(\nu )}$
for the localization at the prime ideal
$S_{(\nu )}$
for the localization at the prime ideal
![]() $(\nu )$
. Set
$(\nu )$
. Set
![]() $N_{(\nu )} = S_{(\nu )}\otimes _S N$
. The algebra
$N_{(\nu )} = S_{(\nu )}\otimes _S N$
. The algebra
![]() $S_{(\nu )}$
is an
$S_{(\nu )}$
is an
![]() $S^{\alpha }$
-algebra for a certain
$S^{\alpha }$
-algebra for a certain
![]() $\alpha \in \Delta $
. Therefore,
$\alpha \in \Delta $
. Therefore,
![]() $N_{(\nu )}$
satisfies (S). Hence, the above embedding
$N_{(\nu )}$
satisfies (S). Hence, the above embedding
![]() $(M_{(\nu )})_{\{A,As\}}(-1)\hookrightarrow (N_{(\nu )})_{I}/(N_{(\nu )})_{I\setminus \{As\}}$
is an isomorphism. Since M admits a standard filtration,
$(M_{(\nu )})_{\{A,As\}}(-1)\hookrightarrow (N_{(\nu )})_{I}/(N_{(\nu )})_{I\setminus \{As\}}$
is an isomorphism. Since M admits a standard filtration,
![]() $M_{\{A,As\}}$
is graded free as an S-module. Therefore,
$M_{\{A,As\}}$
is graded free as an S-module. Therefore,
![]() $M_{\{A,As\}}(-1) = \bigcap _{\nu \in X_{{\mathbb {K}}}}(S_{(\nu )}\otimes _S M_{\{A,As\}}(-1)) = \bigcap _{\nu \in X_{{\mathbb {K}}}}((N_{(\nu )})_{I}/(N_{(\nu )})_{I\setminus \{As\}})\supset N_{I}/N_{I\setminus \{As\}}$
. We get the lemma.
$M_{\{A,As\}}(-1) = \bigcap _{\nu \in X_{{\mathbb {K}}}}(S_{(\nu )}\otimes _S M_{\{A,As\}}(-1)) = \bigcap _{\nu \in X_{{\mathbb {K}}}}((N_{(\nu )})_{I}/(N_{(\nu )})_{I\setminus \{As\}})\supset N_{I}/N_{I\setminus \{As\}}$
. We get the lemma.
(2) First, we prove that there exists an embedding
![]() $(M*B_s)_I/(M*B_s)_{I\setminus J}\hookrightarrow M_{\{A,As\}}(-1)$
. We may assume
$(M*B_s)_I/(M*B_s)_{I\setminus J}\hookrightarrow M_{\{A,As\}}(-1)$
. We may assume
![]() $J = \{A'\in \mathcal {A}\mid A'\le A\}$
since
$J = \{A'\in \mathcal {A}\mid A'\le A\}$
since
![]() $I\setminus J$
is not changed. Then, J is s-invariant. Put
$I\setminus J$
is not changed. Then, J is s-invariant. Put
![]() $I_1 = I\cup Is$
. Then
$I_1 = I\cup Is$
. Then
![]() $I_1$
is an s-invariant closed subset and
$I_1$
is an s-invariant closed subset and
![]() $I_1\cap J = (I\cap J)\cup (Is\cap J) = (I\cap J)\cup (I\cap J)s = \{A,As\}$
. We have
$I_1\cap J = (I\cap J)\cup (Is\cap J) = (I\cap J)\cup (I\cap J)s = \{A,As\}$
. We have
![]() $I_1\setminus \{As\}\supset I$
. Hence, we have an embedding
$I_1\setminus \{As\}\supset I$
. Hence, we have an embedding
![]() $N_I/N_{I\setminus J}\hookrightarrow N_{I_1\setminus \{As\}}/N_{I_1\setminus \{A,As\}}\simeq M_{\{A,As\}(-1)}$
. We prove that this embedding is surjective.
$N_I/N_{I\setminus J}\hookrightarrow N_{I_1\setminus \{As\}}/N_{I_1\setminus \{A,As\}}\simeq M_{\{A,As\}(-1)}$
. We prove that this embedding is surjective.
First, we assume that
![]() ${\mathbb {K}}$
is a field. Take a sequence of closed subsets
${\mathbb {K}}$
is a field. Take a sequence of closed subsets
![]() $I_0 \subset \dotsm \subset I_r$
such that
$I_0 \subset \dotsm \subset I_r$
such that
![]() $\#(I_{i + 1}\setminus I_i) = 1$
,
$\#(I_{i + 1}\setminus I_i) = 1$
,
![]() $N_{I_0} = 0$
,
$N_{I_0} = 0$
,
![]() $N_{I_r} = N$
, and there exists
$N_{I_r} = N$
, and there exists
![]() $k = 1,\dots ,r$
such that
$k = 1,\dots ,r$
such that
![]() $I_{k - 1}\cap \operatorname {\mathrm {supp}}_{\mathcal {A}}(N) = I\cap \operatorname {\mathrm {supp}}_{\mathcal {A}}(N)$
and
$I_{k - 1}\cap \operatorname {\mathrm {supp}}_{\mathcal {A}}(N) = I\cap \operatorname {\mathrm {supp}}_{\mathcal {A}}(N)$
and
![]() $I_k = I_{k - 1}\cup \{A\}$
(Lemma 2.14). Let
$I_k = I_{k - 1}\cup \{A\}$
(Lemma 2.14). Let
![]() $A_i\in \mathcal {A}$
such that
$A_i\in \mathcal {A}$
such that
![]() $I_i = I_{i - 1}\cup \{A_i\}$
. Since
$I_i = I_{i - 1}\cup \{A_i\}$
. Since
![]() $N_{I_i}$
is a filtration of N, for each l, the l-th graded piece
$N_{I_i}$
is a filtration of N, for each l, the l-th graded piece
![]() $N^{l}$
satisfies
$N^{l}$
satisfies
![]() $\dim _{{\mathbb {K}}} N^{l} = \sum _i (N_{I_{i}}/N_{I_{i - 1}})^{l}$
. By the existence of an embedding we have proved,
$\dim _{{\mathbb {K}}} N^{l} = \sum _i (N_{I_{i}}/N_{I_{i - 1}})^{l}$
. By the existence of an embedding we have proved,
![]() $\dim _{{\mathbb {K}}}(N_{I_{i}}/N_{I_{i - 1}})^{l}\le \dim _{{\mathbb {K}}}(M_{\{A_i,A_is\}})^{l + \varepsilon (A_i)}$
, where
$\dim _{{\mathbb {K}}}(N_{I_{i}}/N_{I_{i - 1}})^{l}\le \dim _{{\mathbb {K}}}(M_{\{A_i,A_is\}})^{l + \varepsilon (A_i)}$
, where
![]() $\varepsilon (A_i) = 1$
if
$\varepsilon (A_i) = 1$
if
![]() $A_is> A_i$
and
$A_is> A_i$
and
![]() $\varepsilon (A_i) = -1$
otherwise. We have
$\varepsilon (A_i) = -1$
otherwise. We have
 $$ \begin{align*} & \dim_{{\mathbb{K}}}(M_{\{A_i,A_is\}})^{l + \varepsilon(A_i)}\\ & = \sum_i(\dim_{{\mathbb{K}}}(M_{\{A_i\}})^{l+ \varepsilon(A_i)} + \dim_{{\mathbb{K}}}(M_{\{A_is\}})^{l + \varepsilon(A_i)})\\ & = \sum_{A_is> A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l + 1}) + \sum_{A_is > A_i}\dim_{{\mathbb{K}}}(M_{\{A_is\}}^{l + 1})\\ & \quad + \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l - 1})+ \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_is\}}^{l - 1}). \end{align*} $$
$$ \begin{align*} & \dim_{{\mathbb{K}}}(M_{\{A_i,A_is\}})^{l + \varepsilon(A_i)}\\ & = \sum_i(\dim_{{\mathbb{K}}}(M_{\{A_i\}})^{l+ \varepsilon(A_i)} + \dim_{{\mathbb{K}}}(M_{\{A_is\}})^{l + \varepsilon(A_i)})\\ & = \sum_{A_is> A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l + 1}) + \sum_{A_is > A_i}\dim_{{\mathbb{K}}}(M_{\{A_is\}}^{l + 1})\\ & \quad + \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l - 1})+ \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_is\}}^{l - 1}). \end{align*} $$
By replacing
![]() $A_i$
with
$A_i$
with
![]() $A_is$
in the second and fourth sum, we have
$A_is$
in the second and fourth sum, we have
 $$ \begin{align*} & \sum_i(\dim_{{\mathbb{K}}}(M_{\{A_i\}})^{l+ \varepsilon(A_i)} + \dim_{{\mathbb{K}}}(M_{\{A_is\}})^{l + \varepsilon(A_i)})\\[5.5pt] & = \sum_{A_is> A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l + 1}) + \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l + 1}))\\[5.5pt] & \quad + \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l - 1}) + \sum_{A_is> A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l - 1})\\[5.5pt] & = \sum_i (\dim_{{\mathbb{K}}} M_{\{A_i\}}^{l + 1} + \dim_{{\mathbb{K}}} M_{\{A_i\}}^{l - 1}). \end{align*} $$
$$ \begin{align*} & \sum_i(\dim_{{\mathbb{K}}}(M_{\{A_i\}})^{l+ \varepsilon(A_i)} + \dim_{{\mathbb{K}}}(M_{\{A_is\}})^{l + \varepsilon(A_i)})\\[5.5pt] & = \sum_{A_is> A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l + 1}) + \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l + 1}))\\[5.5pt] & \quad + \sum_{A_is < A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l - 1}) + \sum_{A_is> A_i}\dim_{{\mathbb{K}}}(M_{\{A_i\}}^{l - 1})\\[5.5pt] & = \sum_i (\dim_{{\mathbb{K}}} M_{\{A_i\}}^{l + 1} + \dim_{{\mathbb{K}}} M_{\{A_i\}}^{l - 1}). \end{align*} $$
Since
![]() $\{M_{\{A_i\}}\}$
are subquotients of a filtration
$\{M_{\{A_i\}}\}$
are subquotients of a filtration
![]() $\{M_{I_i}\}$
on M, we have
$\{M_{I_i}\}$
on M, we have
![]() $\sum _i\dim _{{\mathbb {K}}} (M_{\{A_i\}})^{l'} = \dim _{{\mathbb {K}}} M^{l'}$
. Hence,
$\sum _i\dim _{{\mathbb {K}}} (M_{\{A_i\}})^{l'} = \dim _{{\mathbb {K}}} M^{l'}$
. Hence,
![]() $\sum _i (\dim _{{\mathbb {K}}} M_{\{A_i\}}^{l + 1} + \dim _{{\mathbb {K}}} M_{\{A_i\}}^{l - 1}) = \dim _{{\mathbb {K}}} M^{l + 1} + \dim _{{\mathbb {K}}} M^{l - 1}$
.
$\sum _i (\dim _{{\mathbb {K}}} M_{\{A_i\}}^{l + 1} + \dim _{{\mathbb {K}}} M_{\{A_i\}}^{l - 1}) = \dim _{{\mathbb {K}}} M^{l + 1} + \dim _{{\mathbb {K}}} M^{l - 1}$
.
However, since
![]() $N = M*B_s = M\otimes _{R^s}R(1) = M(1)\otimes 1\oplus M(1)\otimes \delta _s$
where
$N = M*B_s = M\otimes _{R^s}R(1) = M(1)\otimes 1\oplus M(1)\otimes \delta _s$
where
![]() $\delta _s$
satisfies
$\delta _s$
satisfies
![]() $\langle \delta _s,\alpha _s^\vee \rangle = 1$
, we have
$\langle \delta _s,\alpha _s^\vee \rangle = 1$
, we have
![]() $\dim _{{\mathbb {K}}} N^l = \dim _{{\mathbb {K}}} M^{l + 1} + \dim _{{\mathbb {K}}} M^{l - 1}$
. Therefore, we get
$\dim _{{\mathbb {K}}} N^l = \dim _{{\mathbb {K}}} M^{l + 1} + \dim _{{\mathbb {K}}} M^{l - 1}$
. Therefore, we get
Hence, the embedding has to be a bijection.
Now, let
![]() ${\mathbb {K}}$
be a general Noetherian integral domain. Assume that we can prove that
${\mathbb {K}}$
be a general Noetherian integral domain. Assume that we can prove that
![]() $(N_{I_i}/N_{I_{i - 1}})\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M_{\{A_i,A_is\}}(\varepsilon (A_i)))\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
for each maximal ideal
$(N_{I_i}/N_{I_{i - 1}})\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M_{\{A_i,A_is\}}(\varepsilon (A_i)))\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
for each maximal ideal
![]() $\mathfrak {m}$
in
$\mathfrak {m}$
in
![]() ${\mathbb {K}}$
. Since
${\mathbb {K}}$
. Since
![]() $M_{\{A_i,A_is\}}^l$
is finitely generated as a
$M_{\{A_i,A_is\}}^l$
is finitely generated as a
![]() ${\mathbb {K}}$
-module, by Nakayama’s lemma,
${\mathbb {K}}$
-module, by Nakayama’s lemma,
![]() $(N_{I_i}/N_{I_{i - 1}})^l_{\mathfrak {m}}\to (M_{\{A_i,A_{i}s\}})^{l + \varepsilon (A_i)}_{\mathfrak {m}}$
is surjective, where
$(N_{I_i}/N_{I_{i - 1}})^l_{\mathfrak {m}}\to (M_{\{A_i,A_{i}s\}})^{l + \varepsilon (A_i)}_{\mathfrak {m}}$
is surjective, where
![]() $(\bullet )_{\mathfrak {m}}$
means the localization at
$(\bullet )_{\mathfrak {m}}$
means the localization at
![]() $\mathfrak {m}$
. Since this is true for any maximal ideal
$\mathfrak {m}$
. Since this is true for any maximal ideal
![]() $\mathfrak {m}$
, the map
$\mathfrak {m}$
, the map
![]() $(N_{I_i}/N_{I_{i - 1}})^l\to M^l_{\{A_i,A_{i}s\}}$
is surjective for any
$(N_{I_i}/N_{I_{i - 1}})^l\to M^l_{\{A_i,A_{i}s\}}$
is surjective for any
![]() $l\in {\mathbb {Z}}$
. Hence, it is an isomorphism. Therefore, it is sufficient to prove
$l\in {\mathbb {Z}}$
. Hence, it is an isomorphism. Therefore, it is sufficient to prove
![]() $(N_{I_i}/N_{I_{i - 1}})\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M_{\{A_i,A_is\}}(\varepsilon (A_i)))\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. In the rest of the proof, we omit the grading.
$(N_{I_i}/N_{I_{i - 1}})\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M_{\{A_i,A_is\}}(\varepsilon (A_i)))\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. In the rest of the proof, we omit the grading.
To prove this, we need some properties on the base change to
![]() ${\mathbb {K}}/\mathfrak {m}$
. Let
${\mathbb {K}}/\mathfrak {m}$
. Let
![]() $L\in \widetilde {\mathcal {K}}'$
. Then,
$L\in \widetilde {\mathcal {K}}'$
. Then,
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
is an
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
is an
![]() $(S/\mathfrak {m}S,R/\mathfrak {m}R)$
-bimodule and we have
$(S/\mathfrak {m}S,R/\mathfrak {m}R)$
-bimodule and we have
![]() $S^{\emptyset }\otimes _{S}L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}) \simeq \bigoplus _{A\in \mathcal {A}}L^{\emptyset }_{A}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. Therefore, it defines an object in
$S^{\emptyset }\otimes _{S}L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}) \simeq \bigoplus _{A\in \mathcal {A}}L^{\emptyset }_{A}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. Therefore, it defines an object in
![]() $\widetilde {\mathcal {K}}^{\prime }_{{\mathbb {K}}/\mathfrak {m}}$
. Here, the suffix
$\widetilde {\mathcal {K}}^{\prime }_{{\mathbb {K}}/\mathfrak {m}}$
. Here, the suffix
![]() ${\mathbb {K}}/\mathfrak {m}$
means that, in the definition of
${\mathbb {K}}/\mathfrak {m}$
means that, in the definition of
![]() $\widetilde {\mathcal {K}}'$
, we replace
$\widetilde {\mathcal {K}}'$
, we replace
![]() ${\mathbb {K}}$
with
${\mathbb {K}}$
with
![]() ${\mathbb {K}}/\mathfrak {m}$
. We also have
${\mathbb {K}}/\mathfrak {m}$
. We also have
![]() $B\otimes _{{\mathbb {K}}}{\mathbb {K}}/\mathfrak {m}\in {\mathcal {S}\mathrm {Bimod}}_{{\mathbb {K}}/\mathfrak {m}}$
(the meaning of the suffix
$B\otimes _{{\mathbb {K}}}{\mathbb {K}}/\mathfrak {m}\in {\mathcal {S}\mathrm {Bimod}}_{{\mathbb {K}}/\mathfrak {m}}$
(the meaning of the suffix
![]() ${\mathbb {K}}/\mathfrak {m}$
is the same as above) and we have
${\mathbb {K}}/\mathfrak {m}$
is the same as above) and we have
![]() $(M*B)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))*(B\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))$
. Let
$(M*B)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))*(B\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))$
. Let
![]() $K\subset \mathcal {A}$
be a closed subset. Then, we have a map
$K\subset \mathcal {A}$
be a closed subset. Then, we have a map
![]() $L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. Since
$L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. Since
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))\subset K$
, the image of this homomorphism is in
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))\subset K$
, the image of this homomorphism is in
![]() $(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. Hence, we get a map
$(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. Hence, we get a map
![]() $L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. We claim:
$L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. We claim:
-
(a) The map is surjective.
-
(b) If
 $L/L_K$
is graded free, then this map is an isomorphism.
$L/L_K$
is graded free, then this map is an isomorphism.
We prove (a) first. By the exact sequence
![]() $0\to L_K\to L\to L/L_K\to 0$
, we have an exact sequence
$0\to L_K\to L\to L/L_K\to 0$
, we have an exact sequence
![]() $L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to 0$
. Since
$L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to 0$
. Since
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}((L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))\subset \mathcal {A}\setminus K$
, the map
$\operatorname {\mathrm {supp}}_{\mathcal {A}}((L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))\subset \mathcal {A}\setminus K$
, the map
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
factors through
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
factors through
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))/(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. Hence,
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))/(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. Hence,
![]() $(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K\subset \operatorname {\mathrm {Ker}} (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})) = \operatorname {\mathrm {Im}}(L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))$
. Therefore, we get (a). If
$(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K\subset \operatorname {\mathrm {Ker}} (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to (L/L_K)\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})) = \operatorname {\mathrm {Im}}(L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))$
. Therefore, we get (a). If
![]() $L/L_K$
is graded free, then
$L/L_K$
is graded free, then
![]() $L/L_K$
is free as a
$L/L_K$
is free as a
![]() ${\mathbb {K}}$
-module. Hence,
${\mathbb {K}}$
-module. Hence,
![]() $L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
is injective. Therefore, we have (b).
$L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\to L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
is injective. Therefore, we have (b).
In particular, if L satisfies (S), then
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
also satisfies (S). Indeed, let
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
also satisfies (S). Indeed, let
![]() $K_1,K_2$
be closed subsets. Then, we have a commutative diagram
$K_1,K_2$
be closed subsets. Then, we have a commutative diagram

Here, the horizontal maps are surjective by (a) in the above, and the left vertical map is surjective since L satisfies (S). Hence, the right vertical map is surjective and it means that
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
satisfies (S).
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
satisfies (S).
We also have that if L satisfies (LE), then
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
satisfies (LE). Let
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
satisfies (LE). Let
![]() $\alpha \in \Delta $
and decompose
$\alpha \in \Delta $
and decompose
![]() $L^{\alpha }$
as
$L^{\alpha }$
as
![]() $L^{\alpha } \simeq \bigoplus _{\Omega \in W^{\prime }_{\alpha }\backslash \mathcal {A}}L^{(\Omega )}$
such that
$L^{\alpha } \simeq \bigoplus _{\Omega \in W^{\prime }_{\alpha }\backslash \mathcal {A}}L^{(\Omega )}$
such that
![]() $\operatorname {\mathrm {supp}} L^{(\Omega )}\subset \Omega $
. Then,
$\operatorname {\mathrm {supp}} L^{(\Omega )}\subset \Omega $
. Then,
![]() $(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))^{\alpha }\simeq \bigoplus _{\Omega \in W^{\prime }_{\alpha }\backslash \mathcal {A}}L^{(\Omega )}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
and it gives a desired decomposition in (LE).
$(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))^{\alpha }\simeq \bigoplus _{\Omega \in W^{\prime }_{\alpha }\backslash \mathcal {A}}L^{(\Omega )}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
and it gives a desired decomposition in (LE).
Let
![]() $K_1\subset K_2\subset \mathcal {A}$
be closed subsets and suppose that
$K_1\subset K_2\subset \mathcal {A}$
be closed subsets and suppose that
![]() $L\in \widetilde {\mathcal {K}}_{\Delta }$
. Since
$L\in \widetilde {\mathcal {K}}_{\Delta }$
. Since
![]() $L\in \widetilde {\mathcal {K}}_{\Delta }$
,
$L\in \widetilde {\mathcal {K}}_{\Delta }$
,
![]() $L/L_{K_1}$
and
$L/L_{K_1}$
and
![]() $L/L_{K_2}$
are both graded free. Hence,
$L/L_{K_2}$
are both graded free. Hence,
![]() $L_{K_1}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_1}\subset (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_2}\simeq L_{K_2}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. By the right exactness of the tensor product, we have
$L_{K_1}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_1}\subset (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_2}\simeq L_{K_2}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})$
. By the right exactness of the tensor product, we have
![]() $(L_{K_2}/L_{K_1})\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (L_{K_2}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))/(L_{K_1}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))\simeq (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_2}/(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_1}$
. Therefore, for any locally closed subset
$(L_{K_2}/L_{K_1})\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (L_{K_2}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))/(L_{K_1}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))\simeq (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_2}/(L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{K_1}$
. Therefore, for any locally closed subset
![]() $K\subset \mathcal {A}$
, we have
$K\subset \mathcal {A}$
, we have
![]() $L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. In particular,
$L_K\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_K$
. In particular,
![]() $L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\in \widetilde {\mathcal {K}}_{\Delta ,{\mathbb {K}}/\mathfrak {m}}$
.
$L\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\in \widetilde {\mathcal {K}}_{\Delta ,{\mathbb {K}}/\mathfrak {m}}$
.
We return to the proof of the lemma. We have
![]() $M\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\in \widetilde {\mathcal {K}}_{\Delta ,{\mathbb {K}}/\mathfrak {m}}$
as we have proved. We have
$M\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\in \widetilde {\mathcal {K}}_{\Delta ,{\mathbb {K}}/\mathfrak {m}}$
as we have proved. We have
![]() $M_{\{A_i,A_is\}}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{\{A_i,A_is\}}$
. Hence, we have the following commutative diagram:
$M_{\{A_i,A_is\}}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (M\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{\{A_i,A_is\}}$
. Hence, we have the following commutative diagram:

Note that the bottom homomorphism is an isomorphism since the lemma is proved if
![]() ${\mathbb {K}}$
is a field.
${\mathbb {K}}$
is a field.
We prove that the left vertical map is an isomorphism by backward induction on i. By inductive hypothesis,
![]() $N_{I_{i'}}/N_{I_{i' - 1}}\simeq M_{\{A_{i'},A_{i'}s\}}$
for any
$N_{I_{i'}}/N_{I_{i' - 1}}\simeq M_{\{A_{i'},A_{i'}s\}}$
for any
![]() $i'> i$
and, in particular, it is graded free. Hence,
$i'> i$
and, in particular, it is graded free. Hence,
![]() $N/N_{I_i}$
is also graded free. Therefore, we have
$N/N_{I_i}$
is also graded free. Therefore, we have
![]() $N_{I_i}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (N\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{I_i}$
. Now we get the desired result by applying the five lemmas to the following commutative diagram with exact columns:
$N_{I_i}\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m})\simeq (N\otimes _{{\mathbb {K}}}({\mathbb {K}}/\mathfrak {m}))_{I_i}$
. Now we get the desired result by applying the five lemmas to the following commutative diagram with exact columns:

Lemma 2.28. Set
![]() $N = M*B_s$
. Then, for any two closed subsets
$N = M*B_s$
. Then, for any two closed subsets
![]() $I_{1},I_{2}$
with
$I_{1},I_{2}$
with
![]() $I_1\supset I_2$
,
$I_1\supset I_2$
,
![]() $N_{I_1}/N_{I_2}$
is a graded free S-module.
$N_{I_1}/N_{I_2}$
is a graded free S-module.
Proof. Take
![]() $A_0,A_1\in \mathcal {A}$
such that
$A_0,A_1\in \mathcal {A}$
such that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}N\subset [A_0,A_1]$
. Replacing
$\operatorname {\mathrm {supp}}_{\mathcal {A}}N\subset [A_0,A_1]$
. Replacing
![]() $I_1$
with
$I_1$
with
![]() $I_1\cap \{A\in \mathcal {A}\mid A\ge A_0\}$
and
$I_1\cap \{A\in \mathcal {A}\mid A\ge A_0\}$
and
![]() $I_2$
with
$I_2$
with
![]() $I_2\cup \{A\in \mathcal {A}\mid A\not \le A_1\}$
, we may assume
$I_2\cup \{A\in \mathcal {A}\mid A\not \le A_1\}$
, we may assume
![]() $I_1\setminus I_2$
is finite. We can take a sequence of closed subsets
$I_1\setminus I_2$
is finite. We can take a sequence of closed subsets
![]() $I_2 = I^{\prime }_0 \subset I^{\prime }_1\subset \dots \subset I^{\prime }_r = I_1$
such that
$I_2 = I^{\prime }_0 \subset I^{\prime }_1\subset \dots \subset I^{\prime }_r = I_1$
such that
![]() $\#(I^{\prime }_{i}\setminus I^{\prime }_{i - 1}) = 1$
. Let
$\#(I^{\prime }_{i}\setminus I^{\prime }_{i - 1}) = 1$
. Let
![]() $A_i$
such that
$A_i$
such that
![]() $I^{\prime }_{i} = I^{\prime }_{i - 1}\cup \{A_i\}$
. Then by Lemma 2.27,
$I^{\prime }_{i} = I^{\prime }_{i - 1}\cup \{A_i\}$
. Then by Lemma 2.27,
![]() $N_{I^{\prime }_i}/N_{I^{\prime }_{i - 1}}\simeq M_{\{A_i,A_is\}}(\varepsilon (A_i))$
, where
$N_{I^{\prime }_i}/N_{I^{\prime }_{i - 1}}\simeq M_{\{A_i,A_is\}}(\varepsilon (A_i))$
, where
![]() $\varepsilon (A_i)\in \{\pm 1\}$
is as in the proof of Lemma 2.27. In particular, this is graded free and therefore,
$\varepsilon (A_i)\in \{\pm 1\}$
is as in the proof of Lemma 2.27. In particular, this is graded free and therefore,
![]() $M_{I_1}/M_{I_2} = M_{I^{\prime }_r}/M_{I^{\prime }_0}$
is also graded free.
$M_{I_1}/M_{I_2} = M_{I^{\prime }_r}/M_{I^{\prime }_0}$
is also graded free.
Proof of Proposition 2.24
Set
![]() $N = M*B_s$
. We prove that N satisfies (S). Let
$N = M*B_s$
. We prove that N satisfies (S). Let
![]() $I_1,I_2$
be closed subsets, and we prove the surjectivity of
$I_1,I_2$
be closed subsets, and we prove the surjectivity of
![]() $N_{I_1}/N_{I_1\cap I_2}\hookrightarrow N_{I_1\cup I_2}/N_{I_2}$
. For each
$N_{I_1}/N_{I_1\cap I_2}\hookrightarrow N_{I_1\cup I_2}/N_{I_2}$
. For each
![]() $\nu \in X^\vee _{{\mathbb {K}}}$
, let
$\nu \in X^\vee _{{\mathbb {K}}}$
, let
![]() $S_{(\nu )}$
be the localization at the prime ideal
$S_{(\nu )}$
be the localization at the prime ideal
![]() $(\nu )$
. Then,
$(\nu )$
. Then,
![]() $S_{(\nu )}$
is an
$S_{(\nu )}$
is an
![]() $S^{\alpha }$
-algebra for some
$S^{\alpha }$
-algebra for some
![]() $\alpha \in \Delta ^{+}$
. Since
$\alpha \in \Delta ^{+}$
. Since
![]() $N_{(\nu )} = S_{(\nu )}\otimes _{S}N$
satisfies (LE),
$N_{(\nu )} = S_{(\nu )}\otimes _{S}N$
satisfies (LE),
![]() $N_{(\nu )}$
satisfies (S) by Lemma 2.10. Hence, this embedding is surjective after applying
$N_{(\nu )}$
satisfies (S) by Lemma 2.10. Hence, this embedding is surjective after applying
![]() $S_{(\nu )}\otimes _S$
. Put
$S_{(\nu )}\otimes _S$
. Put
![]() $L_{(\nu )} = S_{(\nu )}\otimes _{S}L$
for a left S-module L. Since
$L_{(\nu )} = S_{(\nu )}\otimes _{S}L$
for a left S-module L. Since
![]() $N_{I_1}/N_{I_1\cap I_2}$
is graded free by Lemma 2.28, we have
$N_{I_1}/N_{I_1\cap I_2}$
is graded free by Lemma 2.28, we have
![]() $N_{I_1}/N_{I_1\cap I_2} = \bigcap _{\nu } (N_{I_1}/N_{I_1\cap I_2})_{(\nu )}$
. Hence,
$N_{I_1}/N_{I_1\cap I_2} = \bigcap _{\nu } (N_{I_1}/N_{I_1\cap I_2})_{(\nu )}$
. Hence,
![]() $N_{I_1}/N_{I_1\cap I_2} = \bigcap _{\nu } (N_{I_1}/N_{I_1\cap I_2})_{(\nu )} \simeq \bigcap _{\nu } (N_{I_1\cup I_2}/N_{I_2})_{(\nu )}\supset N_{I_1\cup I_2}/N_{I_2}$
. We get the surjectivity.
$N_{I_1}/N_{I_1\cap I_2} = \bigcap _{\nu } (N_{I_1}/N_{I_1\cap I_2})_{(\nu )} \simeq \bigcap _{\nu } (N_{I_1\cup I_2}/N_{I_2})_{(\nu )}\supset N_{I_1\cup I_2}/N_{I_2}$
. We get the surjectivity.
Now
![]() $N_{\{A\}}$
is well-defined and isomorphic to
$N_{\{A\}}$
is well-defined and isomorphic to
![]() $M_{\{A,As\}}(\varepsilon (A))$
, where
$M_{\{A,As\}}(\varepsilon (A))$
, where
![]() $\varepsilon (A)\in \{\pm 1\}$
is as in the proof of Lemma 2.27. Hence,
$\varepsilon (A)\in \{\pm 1\}$
is as in the proof of Lemma 2.27. Hence,
![]() $N_{\{A\}}$
is graded free; namely, N admits a standard filtration.
$N_{\{A\}}$
is graded free; namely, N admits a standard filtration.
As a consequence of Lemma 2.27, we get the following corollary.
Corollary 2.29. If
![]() $M\in \widetilde {\mathcal {K}}_{\Delta }$
, then we have
$M\in \widetilde {\mathcal {K}}_{\Delta }$
, then we have
 $$\begin{align*}(M*B_s)_{\{A\}} \simeq \begin{cases} M_{\{A,As\}}(-1) & (As < A),\\ M_{\{A,As\}}(1) & (As> A). \end{cases} \end{align*}$$
$$\begin{align*}(M*B_s)_{\{A\}} \simeq \begin{cases} M_{\{A,As\}}(-1) & (As < A),\\ M_{\{A,As\}}(1) & (As> A). \end{cases} \end{align*}$$
Therefore, we have
 $$\begin{align*}\operatorname{\mathrm{grk}}((M*B_s)_{\{A\}}) = \begin{cases} v^{-1}(\operatorname{\mathrm{grk}}(M_{\{A\}}) + \operatorname{\mathrm{grk}}(M_{\{As\}})) & (As < A),\\ v(\operatorname{\mathrm{grk}}(M_{\{A\}}) + \operatorname{\mathrm{grk}}(M_{\{As\}})) & (As> A) \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{grk}}((M*B_s)_{\{A\}}) = \begin{cases} v^{-1}(\operatorname{\mathrm{grk}}(M_{\{A\}}) + \operatorname{\mathrm{grk}}(M_{\{As\}})) & (As < A),\\ v(\operatorname{\mathrm{grk}}(M_{\{A\}}) + \operatorname{\mathrm{grk}}(M_{\{As\}})) & (As> A) \end{cases} \end{align*}$$
for each
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $s\in S_{\mathrm {aff}}$
.
$s\in S_{\mathrm {aff}}$
.
The action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
preserves
${\mathcal {S}\mathrm {Bimod}}$
preserves
![]() $\widetilde {\mathcal {K}}_P$
too.
$\widetilde {\mathcal {K}}_P$
too.
Proposition 2.30. We have
![]() $\widetilde {\mathcal {K}}_P*{\mathcal {S}\mathrm {Bimod}}\subset \widetilde {\mathcal {K}}_P$
.
$\widetilde {\mathcal {K}}_P*{\mathcal {S}\mathrm {Bimod}}\subset \widetilde {\mathcal {K}}_P$
.
Proof. Let
![]() $M\in \widetilde {\mathcal {K}}_P$
and
$M\in \widetilde {\mathcal {K}}_P$
and
![]() $s\in S_{\mathrm {aff}}$
. We prove
$s\in S_{\mathrm {aff}}$
. We prove
![]() $M* B_s\in \widetilde {\mathcal {K}}_{P}$
. We have already proved that
$M* B_s\in \widetilde {\mathcal {K}}_{P}$
. We have already proved that
![]() $M*B_s\in \widetilde {\mathcal {K}}_{\Delta }$
.
$M*B_s\in \widetilde {\mathcal {K}}_{\Delta }$
.
Assume that a sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\widetilde {\mathcal {K}}_{\Delta }$
satisfies (ES). By Lemma 2.17,
$\widetilde {\mathcal {K}}_{\Delta }$
satisfies (ES). By Lemma 2.17,
![]() $0\to (M_1)_{\{A,As\}}\to (M_2)_{\{A,As\}}\to (M_3)_{\{A,As\}}\to 0$
is also exact for any
$0\to (M_1)_{\{A,As\}}\to (M_2)_{\{A,As\}}\to (M_3)_{\{A,As\}}\to 0$
is also exact for any
![]() $A\in \mathcal {A}$
. Hence,
$A\in \mathcal {A}$
. Hence,
![]() $0\to (M_1*B_s)_{\{A\}}\to (M_2*B_s)_{\{A\}}\to (M_3*B_s)_{\{A\}}\to 0$
is exact (i.e.,
$0\to (M_1*B_s)_{\{A\}}\to (M_2*B_s)_{\{A\}}\to (M_3*B_s)_{\{A\}}\to 0$
is exact (i.e.,
![]() $M_1*B_s\to M_2*B_s\to M_3*B_s$
also satisfies (ES)). Since
$M_1*B_s\to M_2*B_s\to M_3*B_s$
also satisfies (ES)). Since
![]() $M\in \widetilde {\mathcal {K}}_P$
, the sequence
$M\in \widetilde {\mathcal {K}}_P$
, the sequence
![]() $0\to \operatorname {\mathrm {Hom}}^{\bullet }(M,M_1*B_s)\to \operatorname {\mathrm {Hom}}^{\bullet }(M,M_2*B_s)\to \operatorname {\mathrm {Hom}}^{\bullet }(M,M_3*B_s)\to 0$
is exact. By Proposition 2.22,
$0\to \operatorname {\mathrm {Hom}}^{\bullet }(M,M_1*B_s)\to \operatorname {\mathrm {Hom}}^{\bullet }(M,M_2*B_s)\to \operatorname {\mathrm {Hom}}^{\bullet }(M,M_3*B_s)\to 0$
is exact. By Proposition 2.22,
![]() $M*B_s\in \widetilde {\mathcal {K}}_P$
.
$M*B_s\in \widetilde {\mathcal {K}}_P$
.
2.7 Indecomposable objects
Assume that
![]() ${\mathbb {K}}$
is complete local Noetherian integral domain. For
${\mathbb {K}}$
is complete local Noetherian integral domain. For
![]() $M,N\in \widetilde {\mathcal {K}}'$
,
$M,N\in \widetilde {\mathcal {K}}'$
,
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_S(M,N)$
is finitely generated as an S-module since
$\operatorname {\mathrm {Hom}}^{\bullet }_S(M,N)$
is finitely generated as an S-module since
![]() $M,N$
are finitely generated and S is Noetherian. Hence,
$M,N$
are finitely generated and S is Noetherian. Hence,
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'}(M,N)\subset \operatorname {\mathrm {Hom}}^{\bullet }_S(M,N)$
is also finitely generated. Therefore,
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'}(M,N)\subset \operatorname {\mathrm {Hom}}^{\bullet }_S(M,N)$
is also finitely generated. Therefore,
![]() $\operatorname {\mathrm {Hom}}_{\widetilde {\mathcal {K}}'}(M,N)$
is finitely generated
$\operatorname {\mathrm {Hom}}_{\widetilde {\mathcal {K}}'}(M,N)$
is finitely generated
![]() ${\mathbb {K}}$
-module. Hence,
${\mathbb {K}}$
-module. Hence,
![]() $\widetilde {\mathcal {K}}'$
has Krull-Schmidt property. This is also true for
$\widetilde {\mathcal {K}}'$
has Krull-Schmidt property. This is also true for
![]() $\widetilde {\mathcal {K}}_P$
.
$\widetilde {\mathcal {K}}_P$
.
Let
![]() $({\mathbb {R}}\Delta )_{{\mathrm {int}}} = \{\lambda \in {\mathbb {R}}\Delta \mid \langle \lambda ,\Delta ^\vee \rangle \subset {\mathbb {Z}}\}$
be the set of integral weights. For
$({\mathbb {R}}\Delta )_{{\mathrm {int}}} = \{\lambda \in {\mathbb {R}}\Delta \mid \langle \lambda ,\Delta ^\vee \rangle \subset {\mathbb {Z}}\}$
be the set of integral weights. For
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
, let
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
, let
![]() $\Pi _{\lambda }$
be the set of alcoves A such that
$\Pi _{\lambda }$
be the set of alcoves A such that
![]() $\langle \lambda ,\alpha ^\vee \rangle - 1 < \langle a,\alpha ^\vee \rangle < \langle \lambda ,\alpha ^\vee \rangle $
for any
$\langle \lambda ,\alpha ^\vee \rangle - 1 < \langle a,\alpha ^\vee \rangle < \langle \lambda ,\alpha ^\vee \rangle $
for any
![]() $a\in A$
and simple root
$a\in A$
and simple root
![]() $\alpha $
. The set
$\alpha $
. The set
![]() $\Pi _{\lambda }$
is called a box and each
$\Pi _{\lambda }$
is called a box and each
![]() $A\in \mathcal {A}$
is contained in a box. Each
$A\in \mathcal {A}$
is contained in a box. Each
![]() $\Pi _{\lambda }$
has the unique maximal element
$\Pi _{\lambda }$
has the unique maximal element
![]() $A_{\lambda }^-$
. Let
$A_{\lambda }^-$
. Let
![]() $W^{\prime }_{\lambda } = \operatorname {\mathrm {Stab}}_{W^{\prime }_{\mathrm {aff}}}(\lambda )$
be the stabilizer. Then,
$W^{\prime }_{\lambda } = \operatorname {\mathrm {Stab}}_{W^{\prime }_{\mathrm {aff}}}(\lambda )$
be the stabilizer. Then,
![]() $A_{\lambda }^-$
is the minimal element in
$A_{\lambda }^-$
is the minimal element in
![]() $W_{\lambda }'A_{\lambda }^-$
. The set
$W_{\lambda }'A_{\lambda }^-$
. The set
![]() $W^{\prime }_{\lambda }A_{\lambda }^-$
is the set of alcoves whose closure contains
$W^{\prime }_{\lambda }A_{\lambda }^-$
is the set of alcoves whose closure contains
![]() $\lambda $
.
$\lambda $
.
We define
![]() $Q_{\lambda }\in \widetilde {\mathcal {K}}$
as follows. Consider the orbit
$Q_{\lambda }\in \widetilde {\mathcal {K}}$
as follows. Consider the orbit
![]() $W^{\prime }_{\lambda }A_{\lambda }^-$
through
$W^{\prime }_{\lambda }A_{\lambda }^-$
through
![]() $A_{\lambda }^{-}$
. As an
$A_{\lambda }^{-}$
. As an
![]() $(S,R)$
-bimodule, it is given by
$(S,R)$
-bimodule, it is given by
where the right action of R is given by
![]() $(z_A)f = (f_Az_A)$
. We have
$(z_A)f = (f_Az_A)$
. We have
![]() $Q_{\lambda }^{\emptyset } = (S^{\emptyset })^{W^{\prime }_{\lambda }A_{\lambda }^-}$
. The module
$Q_{\lambda }^{\emptyset } = (S^{\emptyset })^{W^{\prime }_{\lambda }A_{\lambda }^-}$
. The module
![]() $(Q_{\lambda })^{\emptyset }_{A}$
is the A-component if
$(Q_{\lambda })^{\emptyset }_{A}$
is the A-component if
![]() $A\in W^{\prime }_{\lambda }A_{\lambda }^-$
, and
$A\in W^{\prime }_{\lambda }A_{\lambda }^-$
, and
![]() $0$
otherwise.
$0$
otherwise.
The definition of
![]() $Q_{\lambda }$
comes from the structure sheaf of the moment graph associated to
$Q_{\lambda }$
comes from the structure sheaf of the moment graph associated to
![]() $W_{\mathrm {f}}$
. The structure sheaf is defined by
$W_{\mathrm {f}}$
. The structure sheaf is defined by
The natural map
![]() $W^{\prime }_{\lambda }\hookrightarrow W^{\prime }_{{\mathrm {aff}}}\to W_{\mathrm {f}}$
is an isomorphism. The map
$W^{\prime }_{\lambda }\hookrightarrow W^{\prime }_{{\mathrm {aff}}}\to W_{\mathrm {f}}$
is an isomorphism. The map
![]() $W_{\mathrm {f}}\simeq W^{\prime }_{\lambda }\xrightarrow {w\mapsto w(A_{\lambda }^-)}W^{\prime }_{\lambda }A_{\lambda }^{-}$
is a bijection which preserves orders and, by this bijection, we have
$W_{\mathrm {f}}\simeq W^{\prime }_{\lambda }\xrightarrow {w\mapsto w(A_{\lambda }^-)}W^{\prime }_{\lambda }A_{\lambda }^{-}$
is a bijection which preserves orders and, by this bijection, we have
![]() $\mathcal {Z}\simeq Q_{\lambda }$
.
$\mathcal {Z}\simeq Q_{\lambda }$
.
The following are well-known. (See [Reference AbeAbe20b] for example.)
-
• The map
 $S\otimes _{S^{W_{\mathrm {f}}}}S\to \mathcal {Z}$
defined by
$S\otimes _{S^{W_{\mathrm {f}}}}S\to \mathcal {Z}$
defined by
 $f\otimes g\mapsto (x^{-1}(f)g)_{x\in W_{\mathrm {f}}}$
is an isomorphism.
$f\otimes g\mapsto (x^{-1}(f)g)_{x\in W_{\mathrm {f}}}$
is an isomorphism. -
• Let
 $K\subset W_{\mathrm {f}}$
be a closed subset and
$K\subset W_{\mathrm {f}}$
be a closed subset and
 $w\in K$
such that
$w\in K$
such that
 $K\setminus \{w\}$
is closed. Put
$K\setminus \{w\}$
is closed. Put
 $\mathcal {Z}_{K} = \{(z_x)\in \mathcal {Z}\mid z_x = 0 \text { for } x\notin K\}$
and the same for
$\mathcal {Z}_{K} = \{(z_x)\in \mathcal {Z}\mid z_x = 0 \text { for } x\notin K\}$
and the same for
 $\mathcal {Z}_{K\setminus \{w\}}$
. Then,
$\mathcal {Z}_{K\setminus \{w\}}$
. Then,
 $\mathcal {Z}_{K}/\mathcal {Z}_{K\setminus \{w\}}\simeq S(-2\ell (w_0w))$
as a left S-module.
$\mathcal {Z}_{K}/\mathcal {Z}_{K\setminus \{w\}}\simeq S(-2\ell (w_0w))$
as a left S-module.
Let
![]() $d\colon \mathcal {A}\times \mathcal {A}\to {\mathbb {Z}}$
be the function defined in [Reference LusztigLus80, 1.4]. From the second property, we get the following.
$d\colon \mathcal {A}\times \mathcal {A}\to {\mathbb {Z}}$
be the function defined in [Reference LusztigLus80, 1.4]. From the second property, we get the following.
Lemma 2.31. Let
![]() $A\in W^{\prime }_{\lambda }A_{\lambda }^-$
and
$A\in W^{\prime }_{\lambda }A_{\lambda }^-$
and
![]() $I\subset \mathcal {A}$
is a closed subset such that
$I\subset \mathcal {A}$
is a closed subset such that
![]() $A\in I$
and
$A\in I$
and
![]() $I\setminus \{A\}$
is closed. Then, we have
$I\setminus \{A\}$
is closed. Then, we have
![]() $(Q_{\lambda })_I/(Q_{\lambda })_{I\setminus \{A\}}\simeq S(2d(A,A_{\lambda }^-))$
.
$(Q_{\lambda })_I/(Q_{\lambda })_{I\setminus \{A\}}\simeq S(2d(A,A_{\lambda }^-))$
.
It is easy to see that
![]() $Q_{\lambda }$
satisfies (LE) and the argument of the proof of Proposition 2.24 with the above lemma implies that
$Q_{\lambda }$
satisfies (LE) and the argument of the proof of Proposition 2.24 with the above lemma implies that
![]() $Q_{\lambda }$
also satisfies (S). Hence, we have
$Q_{\lambda }$
also satisfies (S). Hence, we have
![]() $Q_{\lambda }\in \mathcal {K}_{\Delta }$
.
$Q_{\lambda }\in \mathcal {K}_{\Delta }$
.
Lemma 2.32. Let
![]() $S_0$
be a flat commutative graded S-algebra. We have
$S_0$
be a flat commutative graded S-algebra. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(S_0\otimes _{S}Q_{\lambda },M)\simeq M_{\{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^-\}}$
for
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}'(S_0)}(S_0\otimes _{S}Q_{\lambda },M)\simeq M_{\{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^-\}}$
for
![]() $M\in \widetilde {\mathcal {K}}'(S_{0})$
. Therefore,
$M\in \widetilde {\mathcal {K}}'(S_{0})$
. Therefore,
![]() $S_0\otimes _{S}Q_{\lambda }\in \widetilde {\mathcal {K}}_P(S_0)$
.
$S_0\otimes _{S}Q_{\lambda }\in \widetilde {\mathcal {K}}_P(S_0)$
.
Proof. Since
![]() $S_0$
is flat, we have
$S_0$
is flat, we have
Put
![]() $I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}$
and
$I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}$
and
![]() $q = (1)_{A\in W_{\mathrm {f}}A_{\lambda }^-}\in S_0\otimes _{S}Q_{\lambda }$
.
$q = (1)_{A\in W_{\mathrm {f}}A_{\lambda }^-}\in S_0\otimes _{S}Q_{\lambda }$
.
Any
![]() $(S_0,R)$
-bimodule is regarded as an
$(S_0,R)$
-bimodule is regarded as an
![]() $S_0\otimes R$
-module. Let
$S_0\otimes R$
-module. Let
![]() $M\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
and
$M\in \widetilde {\mathcal {K}}_{\Delta }(S_0)$
and
![]() $m\in M$
. According to the decomposition
$m\in M$
. According to the decomposition
![]() $M^{\emptyset } = \bigoplus _{A\in \mathcal {A}}M_A^{\emptyset }$
, m can be written as
$M^{\emptyset } = \bigoplus _{A\in \mathcal {A}}M_A^{\emptyset }$
, m can be written as
![]() $m = \sum _{A\in \mathcal {A}}m_A$
with
$m = \sum _{A\in \mathcal {A}}m_A$
with
![]() $m_{A}\in M_{A}^{\emptyset }$
. Consider
$m_{A}\in M_{A}^{\emptyset }$
. Consider
![]() $S^{W_{\mathrm {f}}} = \{f\in S\mid w(f) = f \text { for all } w\in W_{\mathrm {f}}\}$
. Then, we have the following.
$S^{W_{\mathrm {f}}} = \{f\in S\mid w(f) = f \text { for all } w\in W_{\mathrm {f}}\}$
. Then, we have the following.
-
• For
 $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
 $f\in S^{W_{\mathrm {f}}}$
,
$f\in S^{W_{\mathrm {f}}}$
,
 $f^A$
does not depend on A.
$f^A$
does not depend on A. -
• For
 $f\in S$
, we have
$f\in S$
, we have
 $fm = \sum fm_A = \sum m_Af^A$
.
$fm = \sum fm_A = \sum m_Af^A$
.
Therefore, we have an embedding
![]() $S^{W_{\mathrm {f}}}\hookrightarrow R$
naturally and any M is an
$S^{W_{\mathrm {f}}}\hookrightarrow R$
naturally and any M is an
![]() $S_0\otimes _{S^{W_{\mathrm {f}}}}R$
-module. Then, we have a map
$S_0\otimes _{S^{W_{\mathrm {f}}}}R$
-module. Then, we have a map
![]() $S\otimes _{S^{W_{\mathrm {f}}}}R\to Q_{\lambda }$
defined by
$S\otimes _{S^{W_{\mathrm {f}}}}R\to Q_{\lambda }$
defined by
![]() $f\otimes g\mapsto (fg_{w(A_{\lambda }^-)})$
, and by the property of
$f\otimes g\mapsto (fg_{w(A_{\lambda }^-)})$
, and by the property of
![]() $\mathcal {Z}$
we have remarked, this is an isomorphism. Therefore,
$\mathcal {Z}$
we have remarked, this is an isomorphism. Therefore,
![]() $Q_{\lambda }$
is a free
$Q_{\lambda }$
is a free
![]() $S\otimes _{S^{W_{\mathrm {f}}}}R$
-module of rank one with a basis q. We also remark that
$S\otimes _{S^{W_{\mathrm {f}}}}R$
-module of rank one with a basis q. We also remark that
![]() $q\in S_{0}\otimes _{S}Q_{\lambda } = (S_{0}\otimes _{S}Q_{\lambda })_{I}$
. Therefore,
$q\in S_{0}\otimes _{S}Q_{\lambda } = (S_{0}\otimes _{S}Q_{\lambda })_{I}$
. Therefore,
![]() $\varphi \mapsto \varphi (q)$
gives an embedding
$\varphi \mapsto \varphi (q)$
gives an embedding
Let
![]() $m\in M_I$
and
$m\in M_I$
and
![]() $\varphi \colon S_0\otimes _{S}Q_{\lambda }\to M$
be an
$\varphi \colon S_0\otimes _{S}Q_{\lambda }\to M$
be an
![]() $(S_0,R)$
-bimodule homomorphism such that
$(S_0,R)$
-bimodule homomorphism such that
![]() $\varphi (q) = m$
. We prove that this is a morphism in
$\varphi (q) = m$
. We prove that this is a morphism in
![]() $\widetilde {\mathcal {K}}(S_0)$
. Let
$\widetilde {\mathcal {K}}(S_0)$
. Let
![]() $A\in W_{\lambda }'A_{\lambda }^-$
. Then,
$A\in W_{\lambda }'A_{\lambda }^-$
. Then,
![]() $\varphi ((Q_{\lambda })_{A}^{\emptyset })\subset \bigoplus _{A'\in A + {\mathbb {Z}}\Delta ,A'\in I}M_{A'}^{\emptyset }$
. Therefore, the lemma follows from the following lemma.
$\varphi ((Q_{\lambda })_{A}^{\emptyset })\subset \bigoplus _{A'\in A + {\mathbb {Z}}\Delta ,A'\in I}M_{A'}^{\emptyset }$
. Therefore, the lemma follows from the following lemma.
Lemma 2.33. Let
![]() $A\in W^{\prime }_{\lambda }A_{\lambda }^-$
. Then,
$A\in W^{\prime }_{\lambda }A_{\lambda }^-$
. Then,
![]() $(A + {\mathbb {Z}}\Delta )\cap \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^-\} = \{A'\in A + {\mathbb {Z}}\Delta \mid A'\ge A\}$
.
$(A + {\mathbb {Z}}\Delta )\cap \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^-\} = \{A'\in A + {\mathbb {Z}}\Delta \mid A'\ge A\}$
.
Proof. Since
![]() $A_{\lambda }^-$
is the minimal element in
$A_{\lambda }^-$
is the minimal element in
![]() $W^{\prime }_{\lambda }A_{\lambda }^-$
, the right-hand side is contained in the left-hand side. Let
$W^{\prime }_{\lambda }A_{\lambda }^-$
, the right-hand side is contained in the left-hand side. Let
![]() $A'$
be in the left-hand side. Take
$A'$
be in the left-hand side. Take
![]() $x\in W^{\prime }_{\lambda }$
and
$x\in W^{\prime }_{\lambda }$
and
![]() $\mu \in {\mathbb {Z}}\Delta $
such that
$\mu \in {\mathbb {Z}}\Delta $
such that
![]() $A = x(A_{\lambda }^{-})$
and
$A = x(A_{\lambda }^{-})$
and
![]() $A' = A + \mu $
. Then,
$A' = A + \mu $
. Then,
![]() $A' = x(A_{\lambda }^{-}) + \mu $
. Since
$A' = x(A_{\lambda }^{-}) + \mu $
. Since
![]() $A'\ge A_{\lambda }^{-}$
and
$A'\ge A_{\lambda }^{-}$
and
![]() $\lambda $
is in the closure of
$\lambda $
is in the closure of
![]() $A_{\lambda }^{-}$
, we have
$A_{\lambda }^{-}$
, we have
![]() $x(\lambda ) + \mu - \lambda \in {\mathbb {R}}_{\ge 0}\Delta ^+$
by Lemma 2.2. Since
$x(\lambda ) + \mu - \lambda \in {\mathbb {R}}_{\ge 0}\Delta ^+$
by Lemma 2.2. Since
![]() $x\in W^{\prime }_{\lambda } = \operatorname {\mathrm {Stab}}_{W^{\prime }_{{\mathrm {aff}}}}(\lambda )$
,
$x\in W^{\prime }_{\lambda } = \operatorname {\mathrm {Stab}}_{W^{\prime }_{{\mathrm {aff}}}}(\lambda )$
,
![]() $x(\lambda ) = \lambda $
. Therefore,
$x(\lambda ) = \lambda $
. Therefore,
![]() $\mu \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. Hence,
$\mu \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. Hence,
![]() $A' = A + \mu \ge A$
.
$A' = A + \mu \ge A$
.
Let
![]() $A\in \Pi _{\lambda }$
and take
$A\in \Pi _{\lambda }$
and take
![]() $w\in W_{{\mathrm {aff}}}$
such that
$w\in W_{{\mathrm {aff}}}$
such that
![]() $A = A_{\lambda }^{-}w$
. As in the proof of [Reference LusztigLus80, Proposition 4.2], for any
$A = A_{\lambda }^{-}w$
. As in the proof of [Reference LusztigLus80, Proposition 4.2], for any
![]() $x < w$
and
$x < w$
and
![]() $A'\in W^{\prime }_{\lambda }A_{\lambda }^-$
, we have
$A'\in W^{\prime }_{\lambda }A_{\lambda }^-$
, we have
![]() $A'x> A_{\lambda }^-w$
. Let
$A'x> A_{\lambda }^-w$
. Let
![]() $w = s_1\dotsm s_l$
be a reduced expression. Then,
$w = s_1\dotsm s_l$
be a reduced expression. Then,
![]() $Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}$
satisfies the following.
$Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}$
satisfies the following.
Lemma 2.34. We have the following.
-
(1)
 $(Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l})_{\{A\}}\simeq S(l)$
as a left S-module.
$(Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l})_{\{A\}}\simeq S(l)$
as a left S-module. -
(2)
 $\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l})\subset \{A'\in \mathcal {A}\mid A'\ge A\}$
.
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l})\subset \{A'\in \mathcal {A}\mid A'\ge A\}$
.
Proof. (2) is obvious from what we mentioned before the lemma. We prove (1) by induction on l. Set
![]() $M = Q_{\lambda }*B_{s_1}*\dotsb * B_{s_{l - 1}}$
and
$M = Q_{\lambda }*B_{s_1}*\dotsb * B_{s_{l - 1}}$
and
![]() $s = s_l$
. By Lemma 2.27,
$s = s_l$
. By Lemma 2.27,
![]() $(M*B_s)_{\{A\}}\simeq M_{\{A,As\}}(1)$
. By (2),
$(M*B_s)_{\{A\}}\simeq M_{\{A,As\}}(1)$
. By (2),
![]() $A\notin \operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
. Hence,
$A\notin \operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
. Hence,
![]() $M_{\{A,As\}}\simeq M_{\{As\}}$
. Therefore,
$M_{\{A,As\}}\simeq M_{\{As\}}$
. Therefore,
![]() $(M*B_s)_{\{A\}}\simeq M_{\{As\}}(1)$
and the inductive hypothesis implies (1).
$(M*B_s)_{\{A\}}\simeq M_{\{As\}}(1)$
and the inductive hypothesis implies (1).
Theorem 2.35. We have the following.
-
(1) For any
 $A\in \mathcal {A}$
, there exists an indecomposable object
$A\in \mathcal {A}$
, there exists an indecomposable object
 $Q(A)\in \widetilde {\mathcal {K}}_P$
such that
$Q(A)\in \widetilde {\mathcal {K}}_P$
such that
 $\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q(A))\subset \{A'\in \mathcal {A}\mid A'\ge A\}$
and
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q(A))\subset \{A'\in \mathcal {A}\mid A'\ge A\}$
and
 $Q(A)_{\{A\}}\simeq S$
. Moreover,
$Q(A)_{\{A\}}\simeq S$
. Moreover,
 $Q(A)$
is unique up to isomorphisms.
$Q(A)$
is unique up to isomorphisms. -
(2) Any object in
 $\widetilde {\mathcal {K}}_P$
is a direct sum of
$\widetilde {\mathcal {K}}_P$
is a direct sum of
 $Q(A)(n)$
, where
$Q(A)(n)$
, where
 $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
 $n\in {\mathbb {Z}}$
.
$n\in {\mathbb {Z}}$
.
Proof. Fix
![]() $s_1,\dots ,s_l$
as in the above. By Lemma 2.34, there is the unique indecomposable module
$s_1,\dots ,s_l$
as in the above. By Lemma 2.34, there is the unique indecomposable module
![]() $Q(A)$
such that
$Q(A)$
such that
![]() $Q(A)_{\{A\}} \simeq S$
and
$Q(A)_{\{A\}} \simeq S$
and
![]() $Q(A)(l)$
is a direct summand of
$Q(A)(l)$
is a direct summand of
![]() $Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l}$
. It is sufficient to prove that any object
$Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l}$
. It is sufficient to prove that any object
![]() $M\in \widetilde {\mathcal {K}}_P$
is a direct sum of
$M\in \widetilde {\mathcal {K}}_P$
is a direct sum of
![]() $Q(A)(n)$
’s. By induction on the rank of M, it is sufficient to prove that
$Q(A)(n)$
’s. By induction on the rank of M, it is sufficient to prove that
![]() $Q(A)(n)$
is a direct summand of M for some
$Q(A)(n)$
is a direct summand of M for some
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $n\in {\mathbb {Z}}$
if
$n\in {\mathbb {Z}}$
if
![]() $M\ne 0$
.
$M\ne 0$
.
Let
![]() $M\in \widetilde {\mathcal {K}}_P$
and let
$M\in \widetilde {\mathcal {K}}_P$
and let
![]() $A\in \operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
be a minimal element. Then,
$A\in \operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
be a minimal element. Then,
![]() $M_{\{A\}}\ne 0$
. Since M admits a standard filtration,
$M_{\{A\}}\ne 0$
. Since M admits a standard filtration,
![]() $M_{\{A\}}$
is graded free. Hence, there exists n such that
$M_{\{A\}}$
is graded free. Hence, there exists n such that
![]() $S(n)\simeq Q(A)(n)_{\{A\}}$
is a direct summand of
$S(n)\simeq Q(A)(n)_{\{A\}}$
is a direct summand of
![]() $M_{\{A\}}$
. Let
$M_{\{A\}}$
. Let
![]() $i\colon Q(A)(n)_{\{A\}}\to M_{\{A\}}$
(resp.
$i\colon Q(A)(n)_{\{A\}}\to M_{\{A\}}$
(resp.
![]() $p\colon M_{\{A\}}\to Q(A)(n)_{\{A\}}$
) be the embedding from (resp. projection to) the direct summand.
$p\colon M_{\{A\}}\to Q(A)(n)_{\{A\}}$
) be the embedding from (resp. projection to) the direct summand.
Let I be a closed subset which contains
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
such that
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
such that
![]() $I\setminus \{A\}$
is closed. Then,
$I\setminus \{A\}$
is closed. Then,
![]() $I\supset \{A'\in \mathcal {A}\mid A'\ge A\}\supset \operatorname {\mathrm {supp}}_{\mathcal {A}}(Q(A))$
. Therefore, we have two sequences
$I\supset \{A'\in \mathcal {A}\mid A'\ge A\}\supset \operatorname {\mathrm {supp}}_{\mathcal {A}}(Q(A))$
. Therefore, we have two sequences
 $$ \begin{gather*} M_{I\setminus\{A\}}\to M_I = M\to M_{\{A\}},\\ Q(A)(n)_{I\setminus\{A\}}\to Q(A)(n)_I = Q(A)(n)\to Q(A)(n)_{\{A\}}, \end{gather*} $$
$$ \begin{gather*} M_{I\setminus\{A\}}\to M_I = M\to M_{\{A\}},\\ Q(A)(n)_{I\setminus\{A\}}\to Q(A)(n)_I = Q(A)(n)\to Q(A)(n)_{\{A\}}, \end{gather*} $$
which satisfy (ES). Consider the homomorphism
![]() $Q(A)(n)\to Q(A)(n)_{\{A\}}\xrightarrow {i}M_{\{A\}}$
. Since
$Q(A)(n)\to Q(A)(n)_{\{A\}}\xrightarrow {i}M_{\{A\}}$
. Since
![]() $Q(A)(n)\in \widetilde {\mathcal {K}}_P$
, there exists a lift
$Q(A)(n)\in \widetilde {\mathcal {K}}_P$
, there exists a lift
![]() $\widetilde {i}\colon Q(A)(n)\to M$
of the above homomorphism. Similarly, we have a morphism
$\widetilde {i}\colon Q(A)(n)\to M$
of the above homomorphism. Similarly, we have a morphism
![]() $\widetilde {p}\colon M\to Q(A)(n)$
which is a lift of p. The composition
$\widetilde {p}\colon M\to Q(A)(n)$
which is a lift of p. The composition
![]() $\widetilde {p}\circ \widetilde {i}\in \operatorname {\mathrm {End}}(Q(A)(n))$
induces the identity on
$\widetilde {p}\circ \widetilde {i}\in \operatorname {\mathrm {End}}(Q(A)(n))$
induces the identity on
![]() $Q(A)(n)_{\{A\}}$
. Therefore,
$Q(A)(n)_{\{A\}}$
. Therefore,
![]() $1 - \widetilde {p}\circ \widetilde {i}$
is not a unit. Since
$1 - \widetilde {p}\circ \widetilde {i}$
is not a unit. Since
![]() $Q(A)(n)$
is indecomposable, the endomorphism ring of
$Q(A)(n)$
is indecomposable, the endomorphism ring of
![]() $Q(A)(n)$
is local. Therefore,
$Q(A)(n)$
is local. Therefore,
![]() $\widetilde {p}\circ \widetilde {i}$
is an isomorphism. Hence,
$\widetilde {p}\circ \widetilde {i}$
is an isomorphism. Hence,
![]() $Q(A)(n)$
is a direct summand of M.
$Q(A)(n)$
is a direct summand of M.
Corollary 2.36. Any object in
![]() $\widetilde {\mathcal {K}}_P$
is a direct summand of a direct sum of objects of a form
$\widetilde {\mathcal {K}}_P$
is a direct summand of a direct sum of objects of a form
![]() $Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}(n)$
, where
$Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}(n)$
, where
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
![]() $n\in {\mathbb {Z}}$
and
$n\in {\mathbb {Z}}$
and
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
.
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
.
Proof. This is obvious from Theorem 2.35 and the proof of the theorem.
Corollary 2.37. Let
![]() $M,N\in \widetilde {\mathcal {K}}_P$
. Then,
$M,N\in \widetilde {\mathcal {K}}_P$
. Then,
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P}(M,N)$
is graded free of finite rank as an S-module.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P}(M,N)$
is graded free of finite rank as an S-module.
Proof. We may assume
![]() $M = Q_{\lambda } *B_{s_1}*\dotsb * B_{s_l}(n)$
for some
$M = Q_{\lambda } *B_{s_1}*\dotsb * B_{s_l}(n)$
for some
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
![]() $n\in {\mathbb {Z}}$
and
$n\in {\mathbb {Z}}$
and
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
. Hence, by Proposition 2.22, we may assume
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
. Hence, by Proposition 2.22, we may assume
![]() $M = Q_{\lambda }$
. Then,
$M = Q_{\lambda }$
. Then,
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P}(M,N)\simeq N_{\{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}}$
and this is graded free since N admits a standard filtration.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P}(M,N)\simeq N_{\{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}}$
and this is graded free since N admits a standard filtration.
Corollary 2.38. Let
![]() $M,N\in \widetilde {\mathcal {K}}_P$
. Then, for any flat commutative graded S-algebra
$M,N\in \widetilde {\mathcal {K}}_P$
. Then, for any flat commutative graded S-algebra
![]() $S_0$
, we have
$S_0$
, we have
![]() $S_0\otimes _{S}\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P}(M,N)\simeq \operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P(S_0)}(S_0\otimes _{S}M,S_0\otimes _{S}N)$
.
$S_0\otimes _{S}\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P}(M,N)\simeq \operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}_P(S_0)}(S_0\otimes _{S}M,S_0\otimes _{S}N)$
.
Proof. As in the proof of the previous corollary, we may assume
![]() $M = Q_{\lambda }$
. Set
$M = Q_{\lambda }$
. Set
![]() $I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^-\}$
. Then, the corollary is equivalent to
$I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^-\}$
. Then, the corollary is equivalent to
![]() $S_0\otimes _{S}N_I\simeq (S_0\otimes _{S}N)_{I}$
. This is clear.
$S_0\otimes _{S}N_I\simeq (S_0\otimes _{S}N)_{I}$
. This is clear.
2.8 The categorification
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain. We follow the notation of Soergel [Reference SoergelSoe97] for the Hecke algebra and the periodic module. The
${\mathbb {K}}$
is a complete local Noetherian integral domain. We follow the notation of Soergel [Reference SoergelSoe97] for the Hecke algebra and the periodic module. The
![]() ${\mathbb {Z}}[v,v^{-1}]$
-algebra
${\mathbb {Z}}[v,v^{-1}]$
-algebra
![]() $\mathcal {H}$
is generated by
$\mathcal {H}$
is generated by
![]() $\{H_w\mid w\in W_{{\mathrm {aff}}}\}$
and defined by the following relations.
$\{H_w\mid w\in W_{{\mathrm {aff}}}\}$
and defined by the following relations.
-
•
 $(H_s - v^{-1})(H_s + v) = 0$
for any
$(H_s - v^{-1})(H_s + v) = 0$
for any
 $s\in S_{{\mathrm {aff}}}$
.
$s\in S_{{\mathrm {aff}}}$
. -
• If
 $\ell (w_1) + \ell (w_2) = \ell (w_1w_2)$
for
$\ell (w_1) + \ell (w_2) = \ell (w_1w_2)$
for
 $w_1,w_2\in W_{{\mathrm {aff}}}$
, we have
$w_1,w_2\in W_{{\mathrm {aff}}}$
, we have
 $H_{w_1w_2} = H_{w_1}H_{w_2}$
.
$H_{w_1w_2} = H_{w_1}H_{w_2}$
.
It is well-known that
![]() $\{H_w\mid w\in W_{{\mathrm {aff}}}\}$
is a
$\{H_w\mid w\in W_{{\mathrm {aff}}}\}$
is a
![]() ${\mathbb {Z}}[v,v^{-1}]$
-basis of
${\mathbb {Z}}[v,v^{-1}]$
-basis of
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Set
![]() $\mathcal {P} = \bigoplus _{A\in \mathcal {A}}{\mathbb {Z}}[v,v^{-1}]A$
and define a right action of
$\mathcal {P} = \bigoplus _{A\in \mathcal {A}}{\mathbb {Z}}[v,v^{-1}]A$
and define a right action of
![]() $\mathcal {H}$
[Reference SoergelSoe97, Lemma 4.1] on
$\mathcal {H}$
[Reference SoergelSoe97, Lemma 4.1] on
![]() $\mathcal {P}$
by
$\mathcal {P}$
by
 $$\begin{align*}AH_s = \begin{cases} As & (As> A),\\ As + (v^{-1} - v)A & (As < A). \end{cases} \end{align*}$$
$$\begin{align*}AH_s = \begin{cases} As & (As> A),\\ As + (v^{-1} - v)A & (As < A). \end{cases} \end{align*}$$
for
![]() $s\in S_{{\mathrm {aff}}}$
.
$s\in S_{{\mathrm {aff}}}$
.
For an additive category
![]() $\mathcal {B}$
, let
$\mathcal {B}$
, let
![]() $[\mathcal {B}]$
be the split Grothendieck group of
$[\mathcal {B}]$
be the split Grothendieck group of
![]() $\mathcal {B}$
. We have
$\mathcal {B}$
. We have
![]() $[{\mathcal {S}\mathrm {Bimod}}]\simeq \mathcal {H}$
[Reference AbeAbe21, Theorem 4.3] and under this isomorphism,
$[{\mathcal {S}\mathrm {Bimod}}]\simeq \mathcal {H}$
[Reference AbeAbe21, Theorem 4.3] and under this isomorphism,
![]() $[B_s]\in [{\mathcal {S}\mathrm {Bimod}}]$
corresponds to
$[B_s]\in [{\mathcal {S}\mathrm {Bimod}}]$
corresponds to
![]() $H_s + v\in \mathcal {H}$
. By
$H_s + v\in \mathcal {H}$
. By
![]() $[M][B] = [M*B]$
,
$[M][B] = [M*B]$
,
![]() $[\mathcal {K}_P]$
is a right
$[\mathcal {K}_P]$
is a right
![]() $[{\mathcal {S}\mathrm {Bimod}}]$
-module. Fix a length function
$[{\mathcal {S}\mathrm {Bimod}}]$
-module. Fix a length function
![]() $\ell \colon \mathcal {A}\to {\mathbb {Z}}$
in the sense of [Reference LusztigLus80, 2.11]. Define
$\ell \colon \mathcal {A}\to {\mathbb {Z}}$
in the sense of [Reference LusztigLus80, 2.11]. Define
![]() $\operatorname {\mathrm {ch}}\colon [\mathcal {K}_P]\to \mathcal {P}$
by
$\operatorname {\mathrm {ch}}\colon [\mathcal {K}_P]\to \mathcal {P}$
by
Then, by Corollary 2.29,
![]() $\operatorname {\mathrm {ch}}$
is an
$\operatorname {\mathrm {ch}}$
is an
![]() $[{\mathcal {S}\mathrm {Bimod}}]\simeq \mathcal {H}$
-module homomorphism.
$[{\mathcal {S}\mathrm {Bimod}}]\simeq \mathcal {H}$
-module homomorphism.
For each
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
, set
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
, set
![]() $e_{\lambda } = \sum _{A\in W^{\prime }_{\lambda }A_{\lambda }^-}v^{-\ell (A)}A$
. We put
$e_{\lambda } = \sum _{A\in W^{\prime }_{\lambda }A_{\lambda }^-}v^{-\ell (A)}A$
. We put
![]() $\mathcal {P}^{0} = \sum _{\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}}e_{\lambda }\mathcal {H}\subset \mathcal {P}$
.
$\mathcal {P}^{0} = \sum _{\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}}e_{\lambda }\mathcal {H}\subset \mathcal {P}$
.
Lemma 2.39. We have
![]() $\operatorname {\mathrm {ch}}(Q_\lambda ) = v^{2\ell (A_{\lambda }^{-})}e_{\lambda }$
.
$\operatorname {\mathrm {ch}}(Q_\lambda ) = v^{2\ell (A_{\lambda }^{-})}e_{\lambda }$
.
Proof. It follows from Lemma 2.31.
Theorem 2.40. We have
![]() $\operatorname {\mathrm {ch}}\colon [\widetilde {\mathcal {K}}_P]\xrightarrow {\sim } \mathcal {P}^{0}$
.
$\operatorname {\mathrm {ch}}\colon [\widetilde {\mathcal {K}}_P]\xrightarrow {\sim } \mathcal {P}^{0}$
.
Proof. Since
![]() $e_{\lambda } = v^{-2\ell (A_{\lambda }^{-})}\operatorname {\mathrm {ch}}(Q_\lambda )\in \operatorname {\mathrm {Im}}(\operatorname {\mathrm {ch}})$
, the image of
$e_{\lambda } = v^{-2\ell (A_{\lambda }^{-})}\operatorname {\mathrm {ch}}(Q_\lambda )\in \operatorname {\mathrm {Im}}(\operatorname {\mathrm {ch}})$
, the image of
![]() $\operatorname {\mathrm {ch}}$
is contained in
$\operatorname {\mathrm {ch}}$
is contained in
![]() $\mathcal {P}^{0}$
and it surjects to
$\mathcal {P}^{0}$
and it surjects to
![]() $\mathcal {P}^{0}$
. The
$\mathcal {P}^{0}$
. The
![]() $\mathcal {H}$
-module
$\mathcal {H}$
-module
![]() $[\widetilde {\mathcal {K}}_P]$
has a
$[\widetilde {\mathcal {K}}_P]$
has a
![]() ${\mathbb {Z}}[v,v^{-1}]$
-basis
${\mathbb {Z}}[v,v^{-1}]$
-basis
![]() $[Q(A)]$
by Theorem 2.35. Since
$[Q(A)]$
by Theorem 2.35. Since
![]() $\operatorname {\mathrm {ch}}(Q(A))\in v^{\ell (A)}A + \sum _{A'> A}{\mathbb {Z}}[v,v^{-1}]A'$
,
$\operatorname {\mathrm {ch}}(Q(A))\in v^{\ell (A)}A + \sum _{A'> A}{\mathbb {Z}}[v,v^{-1}]A'$
,
![]() $\{\operatorname {\mathrm {ch}}(Q(A))\mid A\in \mathcal {A}\}$
is linearly independent. Hence,
$\{\operatorname {\mathrm {ch}}(Q(A))\mid A\in \mathcal {A}\}$
is linearly independent. Hence,
![]() $\operatorname {\mathrm {ch}}$
is injective.
$\operatorname {\mathrm {ch}}$
is injective.
2.9 A relation with a work of Fiebig-Lanini
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain. In [Reference Fiebig and LaniniFL15], Fiebig and Lanini constructed a category denoted by
${\mathbb {K}}$
is a complete local Noetherian integral domain. In [Reference Fiebig and LaniniFL15], Fiebig and Lanini constructed a category denoted by
![]() $\mathbf {C}$
and proved that this is an exact category. They also constructed a wall-crossing functor
$\mathbf {C}$
and proved that this is an exact category. They also constructed a wall-crossing functor
![]() $\theta _s$
for
$\theta _s$
for
![]() $s\in S_{{\mathrm {aff}}}$
on
$s\in S_{{\mathrm {aff}}}$
on
![]() $\mathbf {C}$
and proved that projective objects are preserved by wall-crossing functors. In this subsection, we prove the following. We identify
$\mathbf {C}$
and proved that projective objects are preserved by wall-crossing functors. In this subsection, we prove the following. We identify
![]() $W^{\prime }_{{\mathrm {aff}}}\simeq W_{{\mathrm {aff}}}$
and
$W^{\prime }_{{\mathrm {aff}}}\simeq W_{{\mathrm {aff}}}$
and
![]() $S\simeq R$
by using
$S\simeq R$
by using
![]() $A_0^+$
, the maximal element in
$A_0^+$
, the maximal element in
![]() $W^{\prime }_{0}A_{0}^{-}$
.
$W^{\prime }_{0}A_{0}^{-}$
.
Theorem 2.41. The category
![]() $\widetilde {\mathcal {K}}_P$
is equivalent to the category of projective objects in
$\widetilde {\mathcal {K}}_P$
is equivalent to the category of projective objects in
![]() $\mathbf {C}$
. The action of
$\mathbf {C}$
. The action of
![]() $B_s$
on
$B_s$
on
![]() $\widetilde {\mathcal {K}}_P$
corresponds to
$\widetilde {\mathcal {K}}_P$
corresponds to
![]() $\theta _s$
for
$\theta _s$
for
![]() $s\in S_{{\mathrm {aff}}}$
.
$s\in S_{{\mathrm {aff}}}$
.
Let
![]() $M\in \widetilde {\mathcal {K}}_P$
, and let
$M\in \widetilde {\mathcal {K}}_P$
, and let
![]() $J\subset \mathcal {A}$
be an open subset. Then,
$J\subset \mathcal {A}$
be an open subset. Then,
![]() $M_J$
is an R-bimodule (as we identify
$M_J$
is an R-bimodule (as we identify
![]() $S\simeq R$
) and the left action of
$S\simeq R$
) and the left action of
![]() $f\in R^{W_{\mathrm {f}}}$
is equal to the right action of f. Hence,
$f\in R^{W_{\mathrm {f}}}$
is equal to the right action of f. Hence,
![]() $M_J$
is an
$M_J$
is an
![]() $R\otimes _{R^{W_{\mathrm {f}}}}R$
-module. The algebra
$R\otimes _{R^{W_{\mathrm {f}}}}R$
-module. The algebra
![]() $R\otimes _{R^{W_{\mathrm {f}}}}R$
is isomorphic to the structure algebra
$R\otimes _{R^{W_{\mathrm {f}}}}R$
is isomorphic to the structure algebra
![]() $\mathcal {Z}$
on the moment graph attached to
$\mathcal {Z}$
on the moment graph attached to
![]() $W_{\mathrm {f}}$
. Hence, we get a functor F from
$W_{\mathrm {f}}$
. Hence, we get a functor F from
![]() $\widetilde {\mathcal {K}}_P$
to the category of
$\widetilde {\mathcal {K}}_P$
to the category of
![]() $\mathcal {Z}$
-coefficient presheaves on
$\mathcal {Z}$
-coefficient presheaves on
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
We prove that F is fully faithful. Since
![]() $M = F(M)(\mathcal {A})$
is an R-module, F induces an injective map between the space of morphisms; namely, F is faithful. Let
$M = F(M)(\mathcal {A})$
is an R-module, F induces an injective map between the space of morphisms; namely, F is faithful. Let
![]() $f\colon F(M)\to F(N)$
be a morphism between sheaves. We define
$f\colon F(M)\to F(N)$
be a morphism between sheaves. We define
![]() $\varphi \colon M\to N$
by
$\varphi \colon M\to N$
by
![]() $M = F(M)(\mathcal {A})\to F(N)(\mathcal {A}) = N$
. Then, this is an R-bimodule morphism. Moreover,
$M = F(M)(\mathcal {A})\to F(N)(\mathcal {A}) = N$
. Then, this is an R-bimodule morphism. Moreover,
![]() $\varphi $
induces
$\varphi $
induces
![]() $M/M_{\mathcal {A}\setminus J} = F(M)(J) \to F(N)(J) = N/N_{\mathcal {A}\setminus J}$
for any open subset J. Hence,
$M/M_{\mathcal {A}\setminus J} = F(M)(J) \to F(N)(J) = N/N_{\mathcal {A}\setminus J}$
for any open subset J. Hence,
![]() $\varphi (M_I)\subset N_I$
for any closed subset
$\varphi (M_I)\subset N_I$
for any closed subset
![]() $I\subset \mathcal {A}$
. Therefore,
$I\subset \mathcal {A}$
. Therefore,
![]() $\varphi $
is a morphism in
$\varphi $
is a morphism in
![]() $\widetilde {\mathcal {K}}_P$
, and therefore, F is full.
$\widetilde {\mathcal {K}}_P$
, and therefore, F is full.
Next, we prove that
![]() $F(M*B_s)\simeq \theta _s(F(M))$
for
$F(M*B_s)\simeq \theta _s(F(M))$
for
![]() $M\in \widetilde {\mathcal {K}}_P$
. Let
$M\in \widetilde {\mathcal {K}}_P$
. Let
![]() $s\in S_{{\mathrm {aff}}}$
, and let
$s\in S_{{\mathrm {aff}}}$
, and let
![]() $\epsilon _s$
be the functor defined in [Reference Fiebig and LaniniFL15, 8.1]. Then an argument of the proof in [Reference AbeAbe21, Proposition 5.3] gives
$\epsilon _s$
be the functor defined in [Reference Fiebig and LaniniFL15, 8.1]. Then an argument of the proof in [Reference AbeAbe21, Proposition 5.3] gives
![]() $\epsilon _s(M) \simeq M\otimes _{R}B_s$
as
$\epsilon _s(M) \simeq M\otimes _{R}B_s$
as
![]() $\mathcal {Z}$
-modules (here, in the right-hand side, we consider a
$\mathcal {Z}$
-modules (here, in the right-hand side, we consider a
![]() $\mathcal {Z}$
-module as an R-bimodule via
$\mathcal {Z}$
-module as an R-bimodule via
![]() $\mathcal {Z} \simeq R\otimes _{R^{W_{\mathrm {f}}}}R$
). Let
$\mathcal {Z} \simeq R\otimes _{R^{W_{\mathrm {f}}}}R$
). Let
![]() $J\subset \mathcal {A}$
be an open subset and
$J\subset \mathcal {A}$
be an open subset and
![]() $J^{\flat }$
(resp.
$J^{\flat }$
(resp.
![]() $J^{\sharp }$
) be the largest (resp. smallest) s-invariant open subset which is contained in (resp. contains) J. Then, we have morphisms
$J^{\sharp }$
) be the largest (resp. smallest) s-invariant open subset which is contained in (resp. contains) J. Then, we have morphisms
such that
![]() $j^{\sharp },j^{\flat }$
are surjective. We have
$j^{\sharp },j^{\flat }$
are surjective. We have
![]() $(M*B_s)_{J^{\sharp }}\simeq M_{J^{\sharp }}*B_s$
and
$(M*B_s)_{J^{\sharp }}\simeq M_{J^{\sharp }}*B_s$
and
![]() $(M*B_s)_{J^{\flat }} \simeq M_{J^{\flat }}*B_s$
by Lemma 2.25. We have
$(M*B_s)_{J^{\flat }} \simeq M_{J^{\flat }}*B_s$
by Lemma 2.25. We have
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(\operatorname {\mathrm {Ker}} j_1)\subset J^{\sharp }\setminus J$
and
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(\operatorname {\mathrm {Ker}} j_1)\subset J^{\sharp }\setminus J$
and
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(\operatorname {\mathrm {Ker}} j_2)\subset J\setminus J^{\flat }$
. Hence, by [Reference Fiebig and LaniniFL15, Lemma 2.8],
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(\operatorname {\mathrm {Ker}} j_2)\subset J\setminus J^{\flat }$
. Hence, by [Reference Fiebig and LaniniFL15, Lemma 2.8],
![]() $(M*B_s)_{J}$
satisfies the condition in [Reference Fiebig and LaniniFL15, 8.3], and we get
$(M*B_s)_{J}$
satisfies the condition in [Reference Fiebig and LaniniFL15, 8.3], and we get
![]() $F(M*B_s)(J) \simeq \theta _s(F(M))(J)$
. Therefore, we get
$F(M*B_s)(J) \simeq \theta _s(F(M))(J)$
. Therefore, we get
![]() $F(M*B_s)\simeq \theta _s(F(M))$
.
$F(M*B_s)\simeq \theta _s(F(M))$
.
Finally, we prove that the image of F is projective and the functor from
![]() $\widetilde {\mathcal {K}}_P$
to the category of projective objects in
$\widetilde {\mathcal {K}}_P$
to the category of projective objects in
![]() $\mathbf {C}$
is essentially surjective. Let
$\mathbf {C}$
is essentially surjective. Let
![]() $\underline {\mathcal {K}}_{\lambda }$
be a projective object in
$\underline {\mathcal {K}}_{\lambda }$
be a projective object in
![]() $\mathbf {C}$
defined in [Reference Fiebig and LaniniFL15, Section 6]. From the definitions, we have
$\mathbf {C}$
defined in [Reference Fiebig and LaniniFL15, Section 6]. From the definitions, we have
![]() $F(Q_{\lambda }) = \underline {\mathcal {K}}_{\lambda }$
. Any
$F(Q_{\lambda }) = \underline {\mathcal {K}}_{\lambda }$
. Any
![]() $M\in \widetilde {\mathcal {K}}_{P}$
is a direct sum of direct summands of objects of the form
$M\in \widetilde {\mathcal {K}}_{P}$
is a direct sum of direct summands of objects of the form
![]() $M*B_{s_1}*\cdots *B_{s_l}(n)$
for
$M*B_{s_1}*\cdots *B_{s_l}(n)$
for
![]() $s_1,\ldots ,s_l\in S_{{\mathrm {aff}}}$
and
$s_1,\ldots ,s_l\in S_{{\mathrm {aff}}}$
and
![]() $n\in {\mathbb {Z}}$
. Since
$n\in {\mathbb {Z}}$
. Since
![]() $F(M*B_{s_1}*\cdots *B_{s_l}(n)) = \theta _{s_l}\cdots \theta _{s_1}\underline {\mathcal {K}}_{\lambda }$
is projective in
$F(M*B_{s_1}*\cdots *B_{s_l}(n)) = \theta _{s_l}\cdots \theta _{s_1}\underline {\mathcal {K}}_{\lambda }$
is projective in
![]() $\mathbf {C}$
by [Reference Fiebig and LaniniFL15, Corollary 8.7],
$\mathbf {C}$
by [Reference Fiebig and LaniniFL15, Corollary 8.7],
![]() $F(M)$
is projective in
$F(M)$
is projective in
![]() $\mathbf {C}$
for any
$\mathbf {C}$
for any
![]() $M\in \widetilde {\mathcal {K}}_{P}$
. Moreover, by the proof of [Reference Fiebig and LaniniFL15, Theorem 8.8], any projective object in
$M\in \widetilde {\mathcal {K}}_{P}$
. Moreover, by the proof of [Reference Fiebig and LaniniFL15, Theorem 8.8], any projective object in
![]() $\mathbf {C}$
is a direct sum of direct summands of objects of the form
$\mathbf {C}$
is a direct sum of direct summands of objects of the form
![]() $\theta _{s_l}\cdots \theta _{s_1}\underline {\mathcal {K}}_{\lambda }$
. Since F is fully faithful, the essential image of F is closed under taking a direct summand. Hence, F is essentially surjective.
$\theta _{s_l}\cdots \theta _{s_1}\underline {\mathcal {K}}_{\lambda }$
. Since F is fully faithful, the essential image of F is closed under taking a direct summand. Hence, F is essentially surjective.
3 The category of Andersen-Jantzen-Soergel
3.1 Our combinatorial category
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain. In this subsection, we introduce some categories using the categories introduced in the previous section. The categories will be related to the combinatorial categories of Andersen-Jantzen-Soergel.
${\mathbb {K}}$
is a complete local Noetherian integral domain. In this subsection, we introduce some categories using the categories introduced in the previous section. The categories will be related to the combinatorial categories of Andersen-Jantzen-Soergel.
Let
![]() $S_0$
be a flat commutative graded S-algebra. Let
$S_0$
be a flat commutative graded S-algebra. Let
![]() $\mathcal {K}'(S_0)$
be the category whose objects are the same as those of
$\mathcal {K}'(S_0)$
be the category whose objects are the same as those of
![]() $\widetilde {\mathcal {K}}'(S_0)$
and the spaces of morphisms are defined by
$\widetilde {\mathcal {K}}'(S_0)$
and the spaces of morphisms are defined by
We also define
![]() $\mathcal {K}(S_0)$
and
$\mathcal {K}(S_0)$
and
![]() $\mathcal {K}_{\Delta }(S_0)$
in the same way.
$\mathcal {K}_{\Delta }(S_0)$
in the same way.
Lemma 3.1. Let
![]() $M,N\in \widetilde {\mathcal {K}}'(S_0)$
,
$M,N\in \widetilde {\mathcal {K}}'(S_0)$
,
![]() $\varphi \colon M\to N$
and
$\varphi \colon M\to N$
and
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
. If
$B\in {\mathcal {S}\mathrm {Bimod}}$
. If
![]() $\varphi (M_{A}^{\emptyset }) \subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
for any
$\varphi (M_{A}^{\emptyset }) \subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
for any
![]() $A\in \mathcal {A}$
, then
$A\in \mathcal {A}$
, then
![]() $\varphi \otimes \operatorname {\mathrm {id}}\colon M*B\to N*B$
satisfies
$\varphi \otimes \operatorname {\mathrm {id}}\colon M*B\to N*B$
satisfies
![]() $(\varphi \otimes \operatorname {\mathrm {id}})((M*B)_{A}^{\emptyset }) \subset \bigoplus _{A'> A}(N*B)_{A'}^{\emptyset }$
for any
$(\varphi \otimes \operatorname {\mathrm {id}})((M*B)_{A}^{\emptyset }) \subset \bigoplus _{A'> A}(N*B)_{A'}^{\emptyset }$
for any
![]() $A\in \mathcal {A}$
.
$A\in \mathcal {A}$
.
Proof. Recall that we have
![]() $(M*B)_A^{\emptyset } = \bigoplus _{x\in W_{\mathrm {aff}}}M_{Ax^{-1}}^{\emptyset }\otimes B_x^{\emptyset }$
. We have
$(M*B)_A^{\emptyset } = \bigoplus _{x\in W_{\mathrm {aff}}}M_{Ax^{-1}}^{\emptyset }\otimes B_x^{\emptyset }$
. We have
![]() $\varphi (M_{Ax^{-1}}^{\emptyset })\otimes B_x^{\emptyset }\subset \bigoplus _{A'x^{-1}\in Ax^{-1} + {\mathbb {Z}}\Delta ,A'x^{-1}> Ax^{-1}}N_{A'x^{-1}}^{\emptyset }\otimes B_x^{\emptyset }$
. Since
$\varphi (M_{Ax^{-1}}^{\emptyset })\otimes B_x^{\emptyset }\subset \bigoplus _{A'x^{-1}\in Ax^{-1} + {\mathbb {Z}}\Delta ,A'x^{-1}> Ax^{-1}}N_{A'x^{-1}}^{\emptyset }\otimes B_x^{\emptyset }$
. Since
![]() $x\colon (Ax^{-1} + {\mathbb {Z}}\Delta )\to (A + {\mathbb {Z}}\Delta )$
preserves the order,
$x\colon (Ax^{-1} + {\mathbb {Z}}\Delta )\to (A + {\mathbb {Z}}\Delta )$
preserves the order,
![]() $A'x^{-1}> Ax^{-1}$
if and only if
$A'x^{-1}> Ax^{-1}$
if and only if
![]() $A'> A$
. Therefore,
$A'> A$
. Therefore,
![]() $(\varphi \otimes \operatorname {\mathrm {id}})(M*B)_A^{\emptyset }\subset \bigoplus _{x\in W_{\mathrm {aff}},A'> A}N_{A'x^{-1}}^{\emptyset }\otimes B_x^{\emptyset } = \bigoplus _{A'>A}(N*B)_{A'}^{\emptyset }$
.
$(\varphi \otimes \operatorname {\mathrm {id}})(M*B)_A^{\emptyset }\subset \bigoplus _{x\in W_{\mathrm {aff}},A'> A}N_{A'x^{-1}}^{\emptyset }\otimes B_x^{\emptyset } = \bigoplus _{A'>A}(N*B)_{A'}^{\emptyset }$
.
Therefore,
![]() $(M,B)\mapsto M*B$
defines a bi-functor
$(M,B)\mapsto M*B$
defines a bi-functor
![]() $\mathcal {K}'(S_0)\times {\mathcal {S}\mathrm {Bimod}}\to \mathcal {K}'(S_0)$
and also
$\mathcal {K}'(S_0)\times {\mathcal {S}\mathrm {Bimod}}\to \mathcal {K}'(S_0)$
and also
![]() $\mathcal {K}_{\Delta }(S_0)\times {\mathcal {S}\mathrm {Bimod}}\to \mathcal {K}_{\Delta }(S_0)$
.
$\mathcal {K}_{\Delta }(S_0)\times {\mathcal {S}\mathrm {Bimod}}\to \mathcal {K}_{\Delta }(S_0)$
.
Proposition 3.2. Let
![]() $M,N\in \mathcal {K}'(S_0)$
and
$M,N\in \mathcal {K}'(S_0)$
and
![]() $s\in S_{{\mathrm {aff}}}$
. Then,
$s\in S_{{\mathrm {aff}}}$
. Then,
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}'(S_0)}(M*B_s,N)\simeq \operatorname {\mathrm {Hom}}_{\mathcal {K}'(S_0)}(M,N*B_s)$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}'(S_0)}(M*B_s,N)\simeq \operatorname {\mathrm {Hom}}_{\mathcal {K}'(S_0)}(M,N*B_s)$
.
Proof. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
as in the proof of Proposition 2.22. Then, the proof of Proposition 2.22 shows that
$\psi $
as in the proof of Proposition 2.22. Then, the proof of Proposition 2.22 shows that
![]() $\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'> A}(N*B_s)_{A'}^{\emptyset }$
for any
$\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'> A}(N*B_s)_{A'}^{\emptyset }$
for any
![]() $A\in \mathcal {A}$
if and only if
$A\in \mathcal {A}$
if and only if
![]() $\psi ((M*B_s)^{\emptyset }_{A}) \subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
for any
$\psi ((M*B_s)^{\emptyset }_{A}) \subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
for any
![]() $A\in \mathcal {A}$
. The proposition follows.
$A\in \mathcal {A}$
. The proposition follows.
For each morphism
![]() $\varphi \colon M\to N$
in
$\varphi \colon M\to N$
in
![]() $\widetilde {\mathcal {K}}(S_0)$
and
$\widetilde {\mathcal {K}}(S_0)$
and
![]() $A\in \mathcal {A}$
, we have a homomorphism
$A\in \mathcal {A}$
, we have a homomorphism
![]() $\varphi _{\{A\}}\colon M_{\{A\}}\to N_{\{A\}}$
. Note that
$\varphi _{\{A\}}\colon M_{\{A\}}\to N_{\{A\}}$
. Note that
![]() $\varphi (M_A^{\emptyset })\subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
if and only if
$\varphi (M_A^{\emptyset })\subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
if and only if
![]() $\varphi _{\{A\}} = 0$
. Hence,
$\varphi _{\{A\}} = 0$
. Hence,
![]() $M\mapsto M_{\{A\}}$
defines a functor from
$M\mapsto M_{\{A\}}$
defines a functor from
![]() $\mathcal {K}(S_0)$
to the category of graded
$\mathcal {K}(S_0)$
to the category of graded
![]() $S_0$
-modules. Using this, we define as follows. A sequence
$S_0$
-modules. Using this, we define as follows. A sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\mathcal {K}(S_0)$
satisfies (ES) if the composition
$\mathcal {K}(S_0)$
satisfies (ES) if the composition
![]() $M_1\to M_2\to M_3$
is zero in
$M_1\to M_2\to M_3$
is zero in
![]() $\mathcal {K}(S_0)$
and
$\mathcal {K}(S_0)$
and
![]() $0\to (M_1)_{\{A\}}\to (M_2)_{\{A\}}\to (M_3)_{\{A\}}\to 0$
is exact for any
$0\to (M_1)_{\{A\}}\to (M_2)_{\{A\}}\to (M_3)_{\{A\}}\to 0$
is exact for any
![]() $A\in \mathcal {A}$
. Note that a sequence
$A\in \mathcal {A}$
. Note that a sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\widetilde {\mathcal {K}}$
may not satisfy (ES) even when it satisfies (ES) in
$\widetilde {\mathcal {K}}$
may not satisfy (ES) even when it satisfies (ES) in
![]() $\mathcal {K}$
since the composition
$\mathcal {K}$
since the composition
![]() $M_1\to M_2\to M_3$
may be zero only in
$M_1\to M_2\to M_3$
may be zero only in
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
For the definition of
![]() $\mathcal {K}_{P}(S_0)$
, we use the same condition to define
$\mathcal {K}_{P}(S_0)$
, we use the same condition to define
![]() $\widetilde {\mathcal {K}}_{P}(S_0)$
. For
$\widetilde {\mathcal {K}}_{P}(S_0)$
. For
![]() $M\in \mathcal {K}_{\Delta }(S_0)$
, we say
$M\in \mathcal {K}_{\Delta }(S_0)$
, we say
![]() $M\in \mathcal {K}_{P}(S_0)$
if, for any sequence
$M\in \mathcal {K}_{P}(S_0)$
if, for any sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\mathcal {K}_{\Delta }(S_0)$
which satisfies (ES), the induced homomorphism
$\mathcal {K}_{\Delta }(S_0)$
which satisfies (ES), the induced homomorphism
![]() $0\to \operatorname {\mathrm {Hom}}_{\mathcal {K}_{\Delta }(S_0)}^{\bullet }(M,M_1)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}_{\Delta }(S_0)}^{\bullet }(M,M_2)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}_{\Delta }(S_0)}^{\bullet }(M,M_3)\to 0$
is exact. Note that this definition is not the same as that in the Introduction. We will prove that two definitions coincide with each other later (Proposition 3.7).
$0\to \operatorname {\mathrm {Hom}}_{\mathcal {K}_{\Delta }(S_0)}^{\bullet }(M,M_1)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}_{\Delta }(S_0)}^{\bullet }(M,M_2)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}_{\Delta }(S_0)}^{\bullet }(M,M_3)\to 0$
is exact. Note that this definition is not the same as that in the Introduction. We will prove that two definitions coincide with each other later (Proposition 3.7).
Proposition 3.3. An indecomposable object in
![]() $\widetilde {\mathcal {K}}'(S_0)$
such that
$\widetilde {\mathcal {K}}'(S_0)$
such that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite and is also indecomposable as an object of
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite and is also indecomposable as an object of
![]() $\mathcal {K}'(S_0)$
.
$\mathcal {K}'(S_0)$
.
Proof. Let
![]() $M\in \widetilde {\mathcal {K}}'(S_0)$
and assume that
$M\in \widetilde {\mathcal {K}}'(S_0)$
and assume that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite. Then,
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite. Then,
![]() $\{\varphi \in \operatorname {\mathrm {End}}_{\widetilde {\mathcal {K}}'(S_0)}(M)\mid \varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'> A}M_{A'}^{\emptyset }\ (A\in \mathcal {A})\}$
is a two-sided ideal of
$\{\varphi \in \operatorname {\mathrm {End}}_{\widetilde {\mathcal {K}}'(S_0)}(M)\mid \varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'> A}M_{A'}^{\emptyset }\ (A\in \mathcal {A})\}$
is a two-sided ideal of
![]() $\operatorname {\mathrm {End}}_{\widetilde {\mathcal {K}}'(S_0)}(M)$
and, since
$\operatorname {\mathrm {End}}_{\widetilde {\mathcal {K}}'(S_0)}(M)$
and, since
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite, this is nilpotent. Therefore, the idempotent lifting property implies the proposition.
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M)$
is finite, this is nilpotent. Therefore, the idempotent lifting property implies the proposition.
Lemma 3.4. Let
![]() $K\subset \mathcal {A}$
be a locally closed subset such that for any
$K\subset \mathcal {A}$
be a locally closed subset such that for any
![]() $A\in K$
, we have
$A\in K$
, we have
![]() $(A + {\mathbb {Z}}\Delta ) \cap K = \{A\}$
. Then, we have the following.
$(A + {\mathbb {Z}}\Delta ) \cap K = \{A\}$
. Then, we have the following.
-
(1) For a morphism
 $\varphi \colon M\to N$
in
$\varphi \colon M\to N$
in
 $\widetilde {\mathcal {K}}(S_0)$
which is zero in
$\widetilde {\mathcal {K}}(S_0)$
which is zero in
 $\mathcal {K}(S_0)$
, the homomorphism
$\mathcal {K}(S_0)$
, the homomorphism
 $M_{K}\to N_{K}$
is zero in
$M_{K}\to N_{K}$
is zero in
 $\widetilde {\mathcal {K}}(S_0)$
.
$\widetilde {\mathcal {K}}(S_0)$
. -
(2) Let
 $M_1\to M_2\to M_3$
be a sequence in
$M_1\to M_2\to M_3$
be a sequence in
 $\widetilde {\mathcal {K}}(S_0)$
and assume that the sequence
$\widetilde {\mathcal {K}}(S_0)$
and assume that the sequence
 $M_1\to M_2\to M_3$
satisfies (ES) as a seqeune in
$M_1\to M_2\to M_3$
satisfies (ES) as a seqeune in
 $\mathcal {K}(S_0)$
. Then,
$\mathcal {K}(S_0)$
. Then,
 $(M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}$
satisfies (ES) as a sequence in
$(M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}$
satisfies (ES) as a sequence in
 $\widetilde {\mathcal {K}}(S_0)$
. In particular,
$\widetilde {\mathcal {K}}(S_0)$
. In particular,
 $0\to (M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}\to 0$
is an exact sequence of
$0\to (M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}\to 0$
is an exact sequence of
 $(S_0,R)$
-bimodules.
$(S_0,R)$
-bimodules.
Proof. (1) We have
![]() $M^{\emptyset }_{K} = \bigoplus _{A\in K}M_{A}^{\emptyset }$
and
$M^{\emptyset }_{K} = \bigoplus _{A\in K}M_{A}^{\emptyset }$
and
![]() $N_{K}^{\emptyset } = \bigoplus _{A\in K}N_{A}^{\emptyset }$
. Since
$N_{K}^{\emptyset } = \bigoplus _{A\in K}N_{A}^{\emptyset }$
. Since
![]() $\varphi = 0$
in
$\varphi = 0$
in
![]() $\mathcal {K}$
, we have
$\mathcal {K}$
, we have
![]() $\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
for any
$\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'> A}N_{A'}^{\emptyset }$
for any
![]() $A\in K$
. We also know that
$A\in K$
. We also know that
![]() $\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A' \in A + {\mathbb {Z}}\Delta }N_{A'}^{\emptyset }$
. By the assumption, there is no
$\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A' \in A + {\mathbb {Z}}\Delta }N_{A'}^{\emptyset }$
. By the assumption, there is no
![]() $A'\in A + {\mathbb {Z}}\Delta $
such that
$A'\in A + {\mathbb {Z}}\Delta $
such that
![]() $A'> A$
and
$A'> A$
and
![]() $A'\in K$
. Hence,
$A'\in K$
. Hence,
![]() $\varphi (M_{A}^{\emptyset }) = 0$
.
$\varphi (M_{A}^{\emptyset }) = 0$
.
(2) By (1), the composition
![]() $(M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}$
is zero.
$(M_1)_{K}\to (M_2)_{K}\to (M_3)_{K}$
is zero.
Lemma 3.5. Assume that a sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\mathcal {K}_{\Delta }(S_0)$
satisfies (ES). Then,
$\mathcal {K}_{\Delta }(S_0)$
satisfies (ES). Then,
![]() $M_1*B\to M_2*B\to M_3*B$
also satisfies (ES).
$M_1*B\to M_2*B\to M_3*B$
also satisfies (ES).
Proof. We may assume
![]() $B = B_s$
where
$B = B_s$
where
![]() $s\in S_{{\mathrm {aff}}}$
. We take lifts of
$s\in S_{{\mathrm {aff}}}$
. We take lifts of
![]() $M_1\to M_2$
and
$M_1\to M_2$
and
![]() $M_2\to M_3$
in
$M_2\to M_3$
in
![]() $\widetilde {\mathcal {K}}(S_0)$
, and we regard
$\widetilde {\mathcal {K}}(S_0)$
, and we regard
![]() $M_1\to M_2\to M_3$
also as a sequence in
$M_1\to M_2\to M_3$
also as a sequence in
![]() $\widetilde {\mathcal {K}}(S_0)$
. As in Corollary 2.29, we have
$\widetilde {\mathcal {K}}(S_0)$
. As in Corollary 2.29, we have
![]() $(M_{i}*B_s)_{\{A\}}\simeq (M_{i})_{\{A,As\}}(\varepsilon (A))$
, where
$(M_{i}*B_s)_{\{A\}}\simeq (M_{i})_{\{A,As\}}(\varepsilon (A))$
, where
![]() $\varepsilon (A)$
is as in the proof of Lemma 2.27. By the previous lemma,
$\varepsilon (A)$
is as in the proof of Lemma 2.27. By the previous lemma,
![]() $0\to (M_{1})_{\{A,As\}}\to (M_{2})_{\{A,As\}}\to (M_{3})_{\{A,As\}}\to 0$
is exact. Therefore,
$0\to (M_{1})_{\{A,As\}}\to (M_{2})_{\{A,As\}}\to (M_{3})_{\{A,As\}}\to 0$
is exact. Therefore,
![]() $0\to (M_1*B_s)_{\{A\}}\to (M_2*B_s)_{\{A\}}\to (M_3*B_s)_{\{A\}}\to 0$
is exact. Hence, a sequence
$0\to (M_1*B_s)_{\{A\}}\to (M_2*B_s)_{\{A\}}\to (M_3*B_s)_{\{A\}}\to 0$
is exact. Hence, a sequence
![]() $M_1*B_s\to M_2*B_s\to M_3*B_s$
in
$M_1*B_s\to M_2*B_s\to M_3*B_s$
in
![]() $\mathcal {K}_{\Delta }(S_0)$
satisfies (ES).
$\mathcal {K}_{\Delta }(S_0)$
satisfies (ES).
Combining Proposition 3.2, we have
![]() $\mathcal {K}_{P}(S_0)*{\mathcal {S}\mathrm {Bimod}}\subset \mathcal {K}_{P}(S_0)$
.
$\mathcal {K}_{P}(S_0)*{\mathcal {S}\mathrm {Bimod}}\subset \mathcal {K}_{P}(S_0)$
.
Lemma 3.6. Let
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
. The subset
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
. The subset
![]() $W^{\prime }_{\lambda }A_{\lambda }^{-}$
is locally closed and we have a natural isomorphism
$W^{\prime }_{\lambda }A_{\lambda }^{-}$
is locally closed and we have a natural isomorphism
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{\lambda },M)\simeq M_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
for
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{\lambda },M)\simeq M_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
for
![]() $M\in \mathcal {K}_{\Delta }(S_0)$
.
$M\in \mathcal {K}_{\Delta }(S_0)$
.
Proof. Set
![]() $I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}$
. We prove
$I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}$
. We prove
![]() $I\setminus W^{\prime }_{\lambda }A_{\lambda ^{-}}$
is closed. Let
$I\setminus W^{\prime }_{\lambda }A_{\lambda ^{-}}$
is closed. Let
![]() $A_1\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
and
$A_1\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
and
![]() $A_2\in I$
satisfies
$A_2\in I$
satisfies
![]() $A_2\le A_1$
. We prove
$A_2\le A_1$
. We prove
![]() $A_2\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
. This proves that
$A_2\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
. This proves that
![]() $I\setminus W^{\prime }_{\lambda }A_{\lambda ^{-}}$
is closed. Take
$I\setminus W^{\prime }_{\lambda }A_{\lambda ^{-}}$
is closed. Take
![]() $A_3\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
such that
$A_3\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
such that
![]() $A_2\in A_3 + {\mathbb {Z}}\Delta $
. Then, by Lemma 2.33, we have
$A_2\in A_3 + {\mathbb {Z}}\Delta $
. Then, by Lemma 2.33, we have
![]() $A_2\ge A_3$
. Take
$A_2\ge A_3$
. Take
![]() $x\in W^{\prime }_{\lambda }$
and
$x\in W^{\prime }_{\lambda }$
and
![]() $\mu \in {\mathbb {Z}}\Delta $
such that
$\mu \in {\mathbb {Z}}\Delta $
such that
![]() $A_1 = x(A_3)$
and
$A_1 = x(A_3)$
and
![]() $A_2 = A_3 + \mu $
. Then,
$A_2 = A_3 + \mu $
. Then,
![]() $A_1\ge A_2\ge A_3$
implies
$A_1\ge A_2\ge A_3$
implies
![]() $x(\lambda ) - (\lambda + \mu )\in {\mathbb {R}}_{\ge 0}\Delta ^+$
and
$x(\lambda ) - (\lambda + \mu )\in {\mathbb {R}}_{\ge 0}\Delta ^+$
and
![]() $(\lambda + \mu ) - \lambda \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. As
$(\lambda + \mu ) - \lambda \in {\mathbb {R}}_{\ge 0}\Delta ^+$
. As
![]() $x(\lambda ) = \lambda $
, we have
$x(\lambda ) = \lambda $
, we have
![]() $\mu = 0$
. Hence,
$\mu = 0$
. Hence,
![]() $A_2 = A_3\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
.
$A_2 = A_3\in W^{\prime }_{\lambda }A_{\lambda }^{-}$
.
We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}(S_0)}(Q_{\lambda },M)\simeq M_{I}$
where
$\operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}(S_0)}(Q_{\lambda },M)\simeq M_{I}$
where
![]() $I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}$
and, under this correspondence,
$I = \{A'\in \mathcal {A}\mid A'\ge A_{\lambda }^{-}\}$
and, under this correspondence,
![]() $\{\varphi \in \operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}(S_0)}(Q_{\lambda },M)\mid \varphi ((Q_{\lambda })_A^{\emptyset })\subset \bigoplus _{A'> A}M_{A'}^{\emptyset }\}$
exactly corresponds to
$\{\varphi \in \operatorname {\mathrm {Hom}}^{\bullet }_{\widetilde {\mathcal {K}}(S_0)}(Q_{\lambda },M)\mid \varphi ((Q_{\lambda })_A^{\emptyset })\subset \bigoplus _{A'> A}M_{A'}^{\emptyset }\}$
exactly corresponds to
![]() $\{m\in M_{I}\mid m_A = 0 \text { for any } A\in W^{\prime }_{\lambda }A_{\lambda ^{-}}\}$
. Since
$\{m\in M_{I}\mid m_A = 0 \text { for any } A\in W^{\prime }_{\lambda }A_{\lambda ^{-}}\}$
. Since
![]() $I\setminus W^{\prime }_{\lambda }A_{\lambda ^{-}}$
is closed,
$I\setminus W^{\prime }_{\lambda }A_{\lambda ^{-}}$
is closed,
![]() $\{m\in M_{I}\mid m_A = 0 \text { for any } A\in W^{\prime }_{\lambda }A_{\lambda ^{-}}\} = M_{I\setminus W^{\prime }_{\lambda }A_{\lambda }^{-}}$
. Hence,
$\{m\in M_{I}\mid m_A = 0 \text { for any } A\in W^{\prime }_{\lambda }A_{\lambda ^{-}}\} = M_{I\setminus W^{\prime }_{\lambda }A_{\lambda }^{-}}$
. Hence,
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(Q_{\lambda },M)\simeq M_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(Q_{\lambda },M)\simeq M_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
.
Proposition 3.7. The objects of
![]() $\mathcal {K}_P$
are the same as those of
$\mathcal {K}_P$
are the same as those of
![]() $\widetilde {\mathcal {K}}_{P}$
.
$\widetilde {\mathcal {K}}_{P}$
.
Proof. First, we prove that any
![]() $M\in \widetilde {\mathcal {K}}_P$
belongs to
$M\in \widetilde {\mathcal {K}}_P$
belongs to
![]() $\mathcal {K}_P$
. By Theorem 2.35, we may assume
$\mathcal {K}_P$
. By Theorem 2.35, we may assume
![]() $M = Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}(n)$
for some
$M = Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}(n)$
for some
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
and
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
and
![]() $n\in {\mathbb {Z}}$
. By Proposition 3.2 and Lemma 3.5, we may assume
$n\in {\mathbb {Z}}$
. By Proposition 3.2 and Lemma 3.5, we may assume
![]() $M = Q_{\lambda }$
.
$M = Q_{\lambda }$
.
We have
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}}(Q_{\lambda },N) \simeq N_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
for
$\operatorname {\mathrm {Hom}}_{\mathcal {K}}(Q_{\lambda },N) \simeq N_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
for
![]() $N\in \mathcal {K}$
. Since
$N\in \mathcal {K}$
. Since
![]() $W^{\prime }_{\lambda }A_{\lambda }^{-}$
satisfies the condition of Lemma 3.4, this implies
$W^{\prime }_{\lambda }A_{\lambda }^{-}$
satisfies the condition of Lemma 3.4, this implies
![]() $Q_{\lambda }\in \mathcal {K}_{P}$
.
$Q_{\lambda }\in \mathcal {K}_{P}$
.
The object
![]() $Q(A)$
is indecomposable in
$Q(A)$
is indecomposable in
![]() $\mathcal {K}_{P}$
by Proposition 3.3. Using the argument in the proof of Theorem 2.35, any object in
$\mathcal {K}_{P}$
by Proposition 3.3. Using the argument in the proof of Theorem 2.35, any object in
![]() $\mathcal {K}_{P}$
is a direct sum of
$\mathcal {K}_{P}$
is a direct sum of
![]() $Q(A)(n)$
where
$Q(A)(n)$
where
![]() $A\in \mathcal {A},n\in {\mathbb {Z}}$
. Hence, the proposition is proved.
$A\in \mathcal {A},n\in {\mathbb {Z}}$
. Hence, the proposition is proved.
Hence, our
![]() $\mathcal {K}_{P}$
is the same as that in the Introduction.
$\mathcal {K}_{P}$
is the same as that in the Introduction.
Corollary 3.8. Let
![]() $M\in \mathcal {K}_{P}$
,
$M\in \mathcal {K}_{P}$
,
![]() $N\in \mathcal {K}_{\Delta }$
and
$N\in \mathcal {K}_{\Delta }$
and
![]() $S_0$
a flat commutative graded S-algebra.
$S_0$
a flat commutative graded S-algebra.
-
(1) The natural map
 $S_0\otimes _{S}\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P}(M,N)\to \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P(S_0)}(S_0\otimes _{S}M,S_0\otimes _{S}N)$
is an isomorphism.
$S_0\otimes _{S}\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P}(M,N)\to \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P(S_0)}(S_0\otimes _{S}M,S_0\otimes _{S}N)$
is an isomorphism. -
(2) We have
 $S_0\otimes _{S}M\in \mathcal {K}_{P}(S_0)$
.
$S_0\otimes _{S}M\in \mathcal {K}_{P}(S_0)$
.
Proof. We may assume
![]() $M = Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}(n)$
for some
$M = Q_{\lambda }*B_{s_1}*\dotsm *B_{s_l}(n)$
for some
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
,
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
and
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
and
![]() $n\in {\mathbb {Z}}$
.
$n\in {\mathbb {Z}}$
.
(1) By Proposition 3.2, we may assume
![]() $M = Q_{\lambda }$
. In this case, the corollary is equivalent to
$M = Q_{\lambda }$
. In this case, the corollary is equivalent to
![]() $S_0\otimes _S(N_{W^{\prime }_{\lambda }A_{\lambda }^{-}})\simeq (S_0\otimes _{S}N)_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
. This is clear.
$S_0\otimes _S(N_{W^{\prime }_{\lambda }A_{\lambda }^{-}})\simeq (S_0\otimes _{S}N)_{W^{\prime }_{\lambda }A_{\lambda }^{-}}$
. This is clear.
(2) By Lemma 3.5, we may assume
![]() $M = Q_{\lambda }$
. Then,
$M = Q_{\lambda }$
. Then,
![]() $S_0\otimes _{S}Q_{\lambda }\in \mathcal {K}_{P}(S_0)$
by Lemma 3.4 and 3.6.
$S_0\otimes _{S}Q_{\lambda }\in \mathcal {K}_{P}(S_0)$
by Lemma 3.4 and 3.6.
We can define
![]() $\operatorname {\mathrm {ch}}\colon [\mathcal {K}_P]\to \mathcal {P}^{0}$
by the same formula as
$\operatorname {\mathrm {ch}}\colon [\mathcal {K}_P]\to \mathcal {P}^{0}$
by the same formula as
![]() $\operatorname {\mathrm {ch}}\colon [\widetilde {\mathcal {K}}_P]\to \mathcal {P}^{0}$
. By the previous proposition with Theorem 2.40, we get the following.
$\operatorname {\mathrm {ch}}\colon [\widetilde {\mathcal {K}}_P]\to \mathcal {P}^{0}$
. By the previous proposition with Theorem 2.40, we get the following.
Theorem 3.9. We have
![]() $[\mathcal {K}_P]\simeq \mathcal {P}^{0}$
.
$[\mathcal {K}_P]\simeq \mathcal {P}^{0}$
.
3.2 A formula on homomorphisms
Assume that
![]() ${\mathbb {K}}$
is amcomplete local Noetherian integral domain. Let
${\mathbb {K}}$
is amcomplete local Noetherian integral domain. Let
![]() $m\mapsto \overline {m}$
be a map from
$m\mapsto \overline {m}$
be a map from
![]() $\mathcal {P}^{0}$
to
$\mathcal {P}^{0}$
to
![]() $\mathcal {P}^{0}$
defined in [Reference SoergelSoe97, Theorem 4.3]. For
$\mathcal {P}^{0}$
defined in [Reference SoergelSoe97, Theorem 4.3]. For
![]() $m\in \mathcal {P}^{0}$
and
$m\in \mathcal {P}^{0}$
and
![]() $m' \in \mathcal {P}$
, take
$m' \in \mathcal {P}$
, take
![]() $c_A,d_A\in {\mathbb {Z}}[v,v^{-1}]$
such that
$c_A,d_A\in {\mathbb {Z}}[v,v^{-1}]$
such that
![]() $\overline {m} = \sum _{A\in \mathcal {A}}c_AA$
and
$\overline {m} = \sum _{A\in \mathcal {A}}c_AA$
and
![]() $m' = \sum _{A\in \mathcal {A}}d_AA$
. Set
$m' = \sum _{A\in \mathcal {A}}d_AA$
. Set
![]() $(m,m')_{\mathcal {P}} = \sum _{A\in \mathcal {A}}c_Ad_A$
. We define
$(m,m')_{\mathcal {P}} = \sum _{A\in \mathcal {A}}c_Ad_A$
. We define
![]() $\omega \colon \mathcal {H}\to \mathcal {H}$
by
$\omega \colon \mathcal {H}\to \mathcal {H}$
by
![]() $\omega (\sum _{x\in W}a_x(v)H_x) = \sum _{x\in W}a_x(v^{-1})H_{x}^{-1}$
. Then, we have
$\omega (\sum _{x\in W}a_x(v)H_x) = \sum _{x\in W}a_x(v^{-1})H_{x}^{-1}$
. Then, we have
where
![]() $m\in \mathcal {P}^{0}$
,
$m\in \mathcal {P}^{0}$
,
![]() $m'\in \mathcal {P}$
and
$m'\in \mathcal {P}$
and
![]() $h\in \mathcal {H}$
. This easily follows from the definitions. Let
$h\in \mathcal {H}$
. This easily follows from the definitions. Let
![]() $w_0\in W_{\mathrm {f}}$
be the longest element.
$w_0\in W_{\mathrm {f}}$
be the longest element.
Theorem 3.10. Let
![]() $P\in \mathcal {K}_{P}$
and
$P\in \mathcal {K}_{P}$
and
![]() $M\in \mathcal {K}_{\Delta }$
. Then,
$M\in \mathcal {K}_{\Delta }$
. Then,
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{\Delta }}(P,M)$
is amgraded free left S-module and the graded rank is given by
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{\Delta }}(P,M)$
is amgraded free left S-module and the graded rank is given by
Proof. Since
![]() $[\mathcal {K}_P]$
is generated by elements of a form
$[\mathcal {K}_P]$
is generated by elements of a form
![]() $[Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l}]$
with
$[Q_{\lambda }*B_{s_1}*\dotsb *B_{s_l}]$
with
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
and
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
and
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
, we may assume P has this form. Moreover, by Lemma 3.2 and the formula before the theorem, we may assume
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
, we may assume P has this form. Moreover, by Lemma 3.2 and the formula before the theorem, we may assume
![]() $P = Q_{\lambda }$
. In this case, we have
$P = Q_{\lambda }$
. In this case, we have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{\Delta }}(P,M) \simeq M_{W_{\lambda }'A_{\lambda }^-}$
, and this is graded free by the definition of
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{\Delta }}(P,M) \simeq M_{W_{\lambda }'A_{\lambda }^-}$
, and this is graded free by the definition of
![]() $\mathcal {K}_{\Delta }$
. Moreover, the graded rank of
$\mathcal {K}_{\Delta }$
. Moreover, the graded rank of
![]() $M_{W_{\lambda }'A_{\lambda }^-}$
is
$M_{W_{\lambda }'A_{\lambda }^-}$
is
![]() $\sum _{A\in W_{\lambda }'A_{\lambda }^-}\operatorname {\mathrm {grk}}(M_{\{A\}})$
.
$\sum _{A\in W_{\lambda }'A_{\lambda }^-}\operatorname {\mathrm {grk}}(M_{\{A\}})$
.
Let
![]() $S_{\lambda }$
be the set of reflections in
$S_{\lambda }$
be the set of reflections in
![]() $W^{\prime }_{\lambda }$
along the walls of
$W^{\prime }_{\lambda }$
along the walls of
![]() $A_{\lambda }^-$
. Then, this is a generator of
$A_{\lambda }^-$
. Then, this is a generator of
![]() $W^{\prime }_{\lambda }$
, and
$W^{\prime }_{\lambda }$
, and
![]() $(W^{\prime }_{\lambda },S_{\lambda })$
is a Coxeter system. The length function of this Coxeter system is denoted by
$(W^{\prime }_{\lambda },S_{\lambda })$
is a Coxeter system. The length function of this Coxeter system is denoted by
![]() $\ell _{\lambda }$
.
$\ell _{\lambda }$
.
We calculate
![]() $(\operatorname {\mathrm {ch}}(Q_{\lambda }),\operatorname {\mathrm {ch}}(M))$
. We put
$(\operatorname {\mathrm {ch}}(Q_{\lambda }),\operatorname {\mathrm {ch}}(M))$
. We put
![]() $(\sum _{A\in \mathcal {A}} c_AA,\sum _{A\in \mathcal {A}}d_AA)' = \sum _{A\in \mathcal {A}} c_Ad_A$
. Let
$(\sum _{A\in \mathcal {A}} c_AA,\sum _{A\in \mathcal {A}}d_AA)' = \sum _{A\in \mathcal {A}} c_Ad_A$
. Let
![]() $E_{\lambda }\in \mathcal {P}$
be the element defined in [Reference SoergelSoe97, 4] and
$E_{\lambda }\in \mathcal {P}$
be the element defined in [Reference SoergelSoe97, 4] and
![]() $A_{\lambda }^+$
the maximal element in
$A_{\lambda }^+$
the maximal element in
![]() $W^{\prime }_{\lambda }A_{\lambda }^-$
. Then, we have
$W^{\prime }_{\lambda }A_{\lambda }^-$
. Then, we have
![]() $E_{\lambda } = \sum _{w\in W^{\prime }_{\lambda }}v^{\ell _{\lambda }(w)}wA_{\lambda }^+$
. Since
$E_{\lambda } = \sum _{w\in W^{\prime }_{\lambda }}v^{\ell _{\lambda }(w)}wA_{\lambda }^+$
. Since
![]() $\ell (w(A_{\lambda }^+)) = \ell (A_{\lambda }^+) - \ell _{\lambda }(w)$
, we have
$\ell (w(A_{\lambda }^+)) = \ell (A_{\lambda }^+) - \ell _{\lambda }(w)$
, we have
![]() $e_{\lambda } = \sum _{w\in W^{\prime }_{\lambda }}v^{-\ell (w(A_{\lambda }^+))}w(A_{\lambda }^+) = v^{-\ell (A_{\lambda }^+)}E_\lambda $
. Therefore,
$e_{\lambda } = \sum _{w\in W^{\prime }_{\lambda }}v^{-\ell (w(A_{\lambda }^+))}w(A_{\lambda }^+) = v^{-\ell (A_{\lambda }^+)}E_\lambda $
. Therefore,
![]() $\operatorname {\mathrm {ch}}(Q_{\lambda }) = v^{2\ell (A_{\lambda }^-)}e_{\lambda } = v^{2\ell (A_{\lambda }^-)-\ell (A_{\lambda }^+)}E_{\lambda }$
. Since
$\operatorname {\mathrm {ch}}(Q_{\lambda }) = v^{2\ell (A_{\lambda }^-)}e_{\lambda } = v^{2\ell (A_{\lambda }^-)-\ell (A_{\lambda }^+)}E_{\lambda }$
. Since
![]() $\overline {E_{\lambda }} = E_{\lambda }$
, we get
$\overline {E_{\lambda }} = E_{\lambda }$
, we get
![]() $\overline {\operatorname {\mathrm {ch}}(Q_{\lambda })} = v^{-2\ell (A_{\lambda }^-)+\ell (A_{\lambda }^+)}E_{\lambda } = v^{-2\ell (A_{\lambda }^-)+2\ell (A_{\lambda }^+)}e_{\lambda } = v^{2\ell (w_0)}e_{\lambda }$
. Hence,
$\overline {\operatorname {\mathrm {ch}}(Q_{\lambda })} = v^{-2\ell (A_{\lambda }^-)+\ell (A_{\lambda }^+)}E_{\lambda } = v^{-2\ell (A_{\lambda }^-)+2\ell (A_{\lambda }^+)}e_{\lambda } = v^{2\ell (w_0)}e_{\lambda }$
. Hence,
 $$ \begin{align*} (\operatorname{\mathrm{ch}}(Q_\lambda),\operatorname{\mathrm{ch}}(M))_{\mathcal{P}} & = v^{2\ell(w_0)}(e_\lambda,\operatorname{\mathrm{ch}}(M))'\\ & = v^{2\ell(w_0)}\left(\sum_{A\in W^{\prime}_{\lambda}A_{\lambda}^-}v^{-\ell(A)}A,\sum_{A\in \mathcal{A}}v^{\ell(A)}\operatorname{\mathrm{grk}}(M_{\{A\}})A\right)'\\ & = v^{2\ell(w_0)}\sum_{A\in W^{\prime}_{\lambda}A_{\lambda}^-}\operatorname{\mathrm{grk}}(M_{\{A\}})\\ & = v^{2\ell(w_0)}\operatorname{\mathrm{grk}}\operatorname{\mathrm{Hom}}^{\bullet}_{\mathcal{K}_P}(Q_{\lambda},M). \end{align*} $$
$$ \begin{align*} (\operatorname{\mathrm{ch}}(Q_\lambda),\operatorname{\mathrm{ch}}(M))_{\mathcal{P}} & = v^{2\ell(w_0)}(e_\lambda,\operatorname{\mathrm{ch}}(M))'\\ & = v^{2\ell(w_0)}\left(\sum_{A\in W^{\prime}_{\lambda}A_{\lambda}^-}v^{-\ell(A)}A,\sum_{A\in \mathcal{A}}v^{\ell(A)}\operatorname{\mathrm{grk}}(M_{\{A\}})A\right)'\\ & = v^{2\ell(w_0)}\sum_{A\in W^{\prime}_{\lambda}A_{\lambda}^-}\operatorname{\mathrm{grk}}(M_{\{A\}})\\ & = v^{2\ell(w_0)}\operatorname{\mathrm{grk}}\operatorname{\mathrm{Hom}}^{\bullet}_{\mathcal{K}_P}(Q_{\lambda},M). \end{align*} $$
We get the theorem.
3.3 The category
 $\mathcal {K}_{P}^{\alpha }$
$\mathcal {K}_{P}^{\alpha }$
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain. In this subsection, we analyze
${\mathbb {K}}$
is a complete local Noetherian integral domain. In this subsection, we analyze
![]() $\mathcal {K}^{\alpha }_{P} = \mathcal {K}_P(S^{\alpha })$
. First, we define an object
$\mathcal {K}^{\alpha }_{P} = \mathcal {K}_P(S^{\alpha })$
. First, we define an object
![]() $Q_{A,\alpha }$
where
$Q_{A,\alpha }$
where
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $\alpha \in \Delta ^+$
. Set
$\alpha \in \Delta ^+$
. Set
![]() $Q_{A,\alpha } = \{(a,b)\in S^2\mid a\equiv b\pmod {\alpha ^\vee }\}$
and define a right action of R on
$Q_{A,\alpha } = \{(a,b)\in S^2\mid a\equiv b\pmod {\alpha ^\vee }\}$
and define a right action of R on
![]() $Q_{A,\alpha }$
by
$Q_{A,\alpha }$
by
![]() $(x,y)f = (f_Ax,s_\alpha (f_A)y)$
for
$(x,y)f = (f_Ax,s_\alpha (f_A)y)$
for
![]() $(x,y)\in Q_{A,\alpha }$
and
$(x,y)\in Q_{A,\alpha }$
and
![]() $f\in R$
. We have
$f\in R$
. We have
![]() $Q_{A,\alpha }^\emptyset = S^\emptyset \oplus S^\emptyset $
and we set
$Q_{A,\alpha }^\emptyset = S^\emptyset \oplus S^\emptyset $
and we set
 $$\begin{align*}(Q_{A,\alpha})_{A'}^{\emptyset} = \begin{cases} S^\emptyset\oplus 0 & (A' = A),\\ 0\oplus S^{\emptyset} & (A' = \alpha\uparrow A),\\ 0 & (\text{otherwise}). \end{cases} \end{align*}$$
$$\begin{align*}(Q_{A,\alpha})_{A'}^{\emptyset} = \begin{cases} S^\emptyset\oplus 0 & (A' = A),\\ 0\oplus S^{\emptyset} & (A' = \alpha\uparrow A),\\ 0 & (\text{otherwise}). \end{cases} \end{align*}$$
It is easy to see that
![]() $Q^{\alpha }_{A,\alpha } = S^{\alpha }\otimes _{S}Q_{A,\alpha }$
is indecomposable.
$Q^{\alpha }_{A,\alpha } = S^{\alpha }\otimes _{S}Q_{A,\alpha }$
is indecomposable.
Lemma 3.11. We have
![]() $Q^\alpha _{A,\alpha }\in \mathcal {K}_{P}^{\alpha }$
.
$Q^\alpha _{A,\alpha }\in \mathcal {K}_{P}^{\alpha }$
.
Proof. It is easy to see that
![]() $Q_{A,\alpha }^{\alpha }\in \mathcal {K}_{\Delta }^{\alpha }$
. Let
$Q_{A,\alpha }^{\alpha }\in \mathcal {K}_{\Delta }^{\alpha }$
. Let
![]() $M\in \mathcal {K}^{\alpha }_{\Delta }$
and we analyze
$M\in \mathcal {K}^{\alpha }_{\Delta }$
and we analyze
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}^{\alpha }_{\Delta }}(Q_{A,\alpha }^{\alpha },M)$
. By (LE),
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}^{\alpha }_{\Delta }}(Q_{A,\alpha }^{\alpha },M)$
. By (LE),
![]() $M \simeq \bigoplus _i M_i$
such that
$M \simeq \bigoplus _i M_i$
such that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A_i$
for some
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A_i$
for some
![]() $A_i\in \mathcal {A}$
. We have
$A_i\in \mathcal {A}$
. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{\Delta }^{\alpha }}(Q^{\alpha }_{A,\alpha },M_i) = 0$
if
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{\Delta }^{\alpha }}(Q^{\alpha }_{A,\alpha },M_i) = 0$
if
![]() $A\notin W^{\prime }_{\alpha ,{\mathrm {aff}}}A_i$
. Therefore, it is sufficient to prove the following: if a sequence
$A\notin W^{\prime }_{\alpha ,{\mathrm {aff}}}A_i$
. Therefore, it is sufficient to prove the following: if a sequence
![]() $M_1\to M_2\to M_3$
in
$M_1\to M_2\to M_3$
in
![]() $\mathcal {K}^{\alpha }_{\Delta }$
satisfies (ES) and
$\mathcal {K}^{\alpha }_{\Delta }$
satisfies (ES) and
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
, then
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M_i)\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
, then
![]() $0\to \operatorname {\mathrm {Hom}}_{\mathcal {K}^{\alpha }_{\Delta }}^{\bullet }(Q_{A,\alpha }^{\alpha },M_1)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}^{\alpha }_{\Delta }}^{\bullet }(Q_{A,\alpha }^{\alpha },M_2)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}^{\alpha }_{\Delta }}^{\bullet }(Q_{A,\alpha }^{\alpha },M_3)\to 0$
is exact. We can apply a similar argument of the proof of Proposition 3.7.
$0\to \operatorname {\mathrm {Hom}}_{\mathcal {K}^{\alpha }_{\Delta }}^{\bullet }(Q_{A,\alpha }^{\alpha },M_1)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}^{\alpha }_{\Delta }}^{\bullet }(Q_{A,\alpha }^{\alpha },M_2)\to \operatorname {\mathrm {Hom}}_{\mathcal {K}^{\alpha }_{\Delta }}^{\bullet }(Q_{A,\alpha }^{\alpha },M_3)\to 0$
is exact. We can apply a similar argument of the proof of Proposition 3.7.
We can apply the argument in the proof of Theorem 2.35 and get the following proposition.
Proposition 3.12. Any object in
![]() $\mathcal {K}_{P}^{\alpha }$
is a direct sum of
$\mathcal {K}_{P}^{\alpha }$
is a direct sum of
![]() $Q_{A,\alpha }^{\alpha }(n)$
where
$Q_{A,\alpha }^{\alpha }(n)$
where
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $n\in {\mathbb {Z}}$
.
$n\in {\mathbb {Z}}$
.
3.4 The combinatorial category of Andersen-Jantzen-Soergel
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain. We recall the combinatorial category of Andersen-Jantzen-Soergel [Reference Andersen, Jantzen and SoergelAJS94]. We use the version introduced by Fiebig in [Reference FiebigFie11]. We write
${\mathbb {K}}$
is a complete local Noetherian integral domain. We recall the combinatorial category of Andersen-Jantzen-Soergel [Reference Andersen, Jantzen and SoergelAJS94]. We use the version introduced by Fiebig in [Reference FiebigFie11]. We write
![]() $\mathcal {K}_{{\mathrm {AJS}}}$
for this category.
$\mathcal {K}_{{\mathrm {AJS}}}$
for this category.
Let
![]() $S_0$
be a flat commutative graded S-algebra and we define the category
$S_0$
be a flat commutative graded S-algebra and we define the category
![]() $\mathcal {K}_{{\mathrm {AJS}}}(S_0)$
as follows. An object of
$\mathcal {K}_{{\mathrm {AJS}}}(S_0)$
as follows. An object of
![]() $\mathcal {K}_{{\mathrm {AJS}}}(S_0)$
is
$\mathcal {K}_{{\mathrm {AJS}}}(S_0)$
is
![]() $\mathcal {M} = ((\mathcal {M}(A))_{A\in \mathcal {A}},(\mathcal {M}(A,\alpha ))_{A\in \mathcal {A},\alpha \in \Delta ^+})$
, where
$\mathcal {M} = ((\mathcal {M}(A))_{A\in \mathcal {A}},(\mathcal {M}(A,\alpha ))_{A\in \mathcal {A},\alpha \in \Delta ^+})$
, where
![]() $\mathcal {M}(A)$
is a graded
$\mathcal {M}(A)$
is a graded
![]() $(S_0)^{\emptyset }$
-module and
$(S_0)^{\emptyset }$
-module and
![]() $\mathcal {M}(A,\alpha )\subset \mathcal {M}(A)\oplus \mathcal {M}(\alpha \uparrow A)$
is a graded sub-
$\mathcal {M}(A,\alpha )\subset \mathcal {M}(A)\oplus \mathcal {M}(\alpha \uparrow A)$
is a graded sub-
![]() $(S_0)^{\alpha }$
-module. A morphism
$(S_0)^{\alpha }$
-module. A morphism
![]() $f\colon \mathcal {M}\to \mathcal {N}$
in
$f\colon \mathcal {M}\to \mathcal {N}$
in
![]() $\mathcal {K}_{{\mathrm {AJS}}}(S_0)$
is a collection of degree zero
$\mathcal {K}_{{\mathrm {AJS}}}(S_0)$
is a collection of degree zero
![]() $(S_0)^{\emptyset }$
-homomorphisms
$(S_0)^{\emptyset }$
-homomorphisms
![]() $f_{A}\colon \mathcal {M}(A)\to \mathcal {N}(A)$
which sends
$f_{A}\colon \mathcal {M}(A)\to \mathcal {N}(A)$
which sends
![]() $\mathcal {M}(A,\alpha )$
to
$\mathcal {M}(A,\alpha )$
to
![]() $\mathcal {N}(A,\alpha )$
for any
$\mathcal {N}(A,\alpha )$
for any
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $\alpha \in \Delta ^+$
. Put
$\alpha \in \Delta ^+$
. Put
![]() $\mathcal {K}_{{\mathrm {AJS}}} = \mathcal {K}_{{\mathrm {AJS}}}(S)$
and
$\mathcal {K}_{{\mathrm {AJS}}} = \mathcal {K}_{{\mathrm {AJS}}}(S)$
and
![]() $\mathcal {K}_{{\mathrm {AJS}}}^{*} = \mathcal {K}_{{\mathrm {AJS}}}(S^*)$
for
$\mathcal {K}_{{\mathrm {AJS}}}^{*} = \mathcal {K}_{{\mathrm {AJS}}}(S^*)$
for
![]() $*\in \{\emptyset \}\cup \Delta $
.
$*\in \{\emptyset \}\cup \Delta $
.
For each
![]() $s\in S_{{\mathrm {aff}}}$
, the translation functor
$s\in S_{{\mathrm {aff}}}$
, the translation functor
![]() $\vartheta _s\colon \mathcal {K}_{{\mathrm {AJS}}}(S_0)\to \mathcal {K}_{{\mathrm {AJS}}}(S_0)$
is defined as
$\vartheta _s\colon \mathcal {K}_{{\mathrm {AJS}}}(S_0)\to \mathcal {K}_{{\mathrm {AJS}}}(S_0)$
is defined as
and
 $$\begin{align*}\vartheta_s(\mathcal{M})(A,\alpha) = \begin{cases} \mathcal{M}(A,\alpha)\oplus \mathcal{M}(As,\alpha) & (As\notin W^{\prime}_{\alpha,{\mathrm{aff}}}A),\\ \{(x,y)\in \mathcal{M}(A,\alpha)^2\mid x - y\in \alpha^\vee \mathcal{M}(A,\alpha)\} & (As = \alpha\uparrow A),\\ \alpha^\vee\mathcal{M}(As,\alpha)\oplus \mathcal{M}(\alpha\uparrow A,\alpha) & (As = \alpha\downarrow A). \end{cases} \end{align*}$$
$$\begin{align*}\vartheta_s(\mathcal{M})(A,\alpha) = \begin{cases} \mathcal{M}(A,\alpha)\oplus \mathcal{M}(As,\alpha) & (As\notin W^{\prime}_{\alpha,{\mathrm{aff}}}A),\\ \{(x,y)\in \mathcal{M}(A,\alpha)^2\mid x - y\in \alpha^\vee \mathcal{M}(A,\alpha)\} & (As = \alpha\uparrow A),\\ \alpha^\vee\mathcal{M}(As,\alpha)\oplus \mathcal{M}(\alpha\uparrow A,\alpha) & (As = \alpha\downarrow A). \end{cases} \end{align*}$$
We define
![]() $\mathcal {F}(S_0)\colon \mathcal {K}_P(S_0)\to \mathcal {K}_{{\mathrm {AJS}}}(S_0)$
as follows. First, we put
$\mathcal {F}(S_0)\colon \mathcal {K}_P(S_0)\to \mathcal {K}_{{\mathrm {AJS}}}(S_0)$
as follows. First, we put
To define
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
, we take
$(\mathcal {F}(S_0)(M))(A,\alpha )$
, we take
![]() $X\in \widetilde {\mathcal {K}}_{P}(S_0^{\alpha })$
and an isomorphism
$X\in \widetilde {\mathcal {K}}_{P}(S_0^{\alpha })$
and an isomorphism
![]() $\varphi \colon X\to M^{\alpha }$
in
$\varphi \colon X\to M^{\alpha }$
in
![]() $\widetilde {\mathcal {K}}_P(S_0^{\alpha })$
such that
$\widetilde {\mathcal {K}}_P(S_0^{\alpha })$
such that
![]() $X = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(X\cap \bigoplus _{A\in \Omega }X_A^{\emptyset })$
. Such X exists since M satisfies (LE). Then we have an isomorphism
$X = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(X\cap \bigoplus _{A\in \Omega }X_A^{\emptyset })$
. Such X exists since M satisfies (LE). Then we have an isomorphism
![]() $X_A^{\emptyset }\simeq (X_{\ge A}/X_{>A})^{\emptyset }\simeq ((M^{\alpha })_{\ge A}/(M^{\alpha })_{>A})^{\emptyset }\simeq M^{\emptyset }_{A}$
. In general, for
$X_A^{\emptyset }\simeq (X_{\ge A}/X_{>A})^{\emptyset }\simeq ((M^{\alpha })_{\ge A}/(M^{\alpha })_{>A})^{\emptyset }\simeq M^{\emptyset }_{A}$
. In general, for
![]() $Y\in \mathcal {K}_P(S_0)$
,
$Y\in \mathcal {K}_P(S_0)$
,
![]() $y\in Y^{\emptyset }$
and
$y\in Y^{\emptyset }$
and
![]() $A\in \mathcal {A}$
, write
$A\in \mathcal {A}$
, write
![]() $y_A$
for the
$y_A$
for the
![]() $Y_A^{\emptyset }$
-component of y along the decomposition
$Y_A^{\emptyset }$
-component of y along the decomposition
![]() $Y^{\emptyset } = \bigoplus _{A\in \mathcal {A}}Y^{\emptyset }_A$
. Then, this isomorphism can be written as
$Y^{\emptyset } = \bigoplus _{A\in \mathcal {A}}Y^{\emptyset }_A$
. Then, this isomorphism can be written as
![]() $x\mapsto \varphi (x)_A$
. Here, we use the same letter
$x\mapsto \varphi (x)_A$
. Here, we use the same letter
![]() $\varphi $
for the induced map
$\varphi $
for the induced map
![]() $X^{\emptyset }\to M^{\emptyset }$
.
$X^{\emptyset }\to M^{\emptyset }$
.
Now let
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
be the image of
$(\mathcal {F}(S_0)(M))(A,\alpha )$
be the image of
In other words,
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
is the set of
$(\mathcal {F}(S_0)(M))(A,\alpha )$
is the set of
![]() $(\varphi (x_A)_A,\varphi (x_{\alpha \uparrow A})_{\alpha \uparrow A})$
where
$(\varphi (x_A)_A,\varphi (x_{\alpha \uparrow A})_{\alpha \uparrow A})$
where
![]() $x\in X_{\ge A}$
. We may assume
$x\in X_{\ge A}$
. We may assume
![]() $x\in \bigoplus _{A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A}X_{A'}^{\emptyset }$
. Of course, we have to prove that this space does not depend on a choice of X. We use the following lemma.
$x\in \bigoplus _{A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A}X_{A'}^{\emptyset }$
. Of course, we have to prove that this space does not depend on a choice of X. We use the following lemma.
Lemma 3.13. Let
![]() $X,Y\in \widetilde {\mathcal {K}}_P(S_0)$
,
$X,Y\in \widetilde {\mathcal {K}}_P(S_0)$
,
![]() $f\colon X\to Y$
be a morphism,
$f\colon X\to Y$
be a morphism,
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $\alpha \in \Delta ^{+}$
. Assume that
$\alpha \in \Delta ^{+}$
. Assume that
![]() $x\in X^{\emptyset }_{\ge A}$
satisfies
$x\in X^{\emptyset }_{\ge A}$
satisfies
![]() $x_{A'} = 0$
for
$x_{A'} = 0$
for
![]() $A'\notin W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
.
$A'\notin W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
.
-
(1) We have
 $f(x)_A = f(x_A)_A$
and
$f(x)_A = f(x_A)_A$
and
 $f(x)_{\alpha \uparrow A} = f(x_{\alpha \uparrow A})_{\alpha \uparrow A}$
.
$f(x)_{\alpha \uparrow A} = f(x_{\alpha \uparrow A})_{\alpha \uparrow A}$
. -
(2) Let
 $g\colon Y\to Z$
be another morphism in
$g\colon Y\to Z$
be another morphism in
 $\widetilde {\mathcal {K}}_P(S_0)$
. Then,
$\widetilde {\mathcal {K}}_P(S_0)$
. Then,
 $g(f(x)_{A'})_{A'} = g(f(x))_{A'}$
for
$g(f(x)_{A'})_{A'} = g(f(x))_{A'}$
for
 $A'\in \{A,\alpha \uparrow A\}$
$A'\in \{A,\alpha \uparrow A\}$
Proof. We prove (1). Let
![]() $A"\in \mathcal {A}$
. Then
$A"\in \mathcal {A}$
. Then
![]() $f(x)_{A"} = \sum _{A'\in \mathcal {A}}f(x_{A'})_{A"}$
. We have
$f(x)_{A"} = \sum _{A'\in \mathcal {A}}f(x_{A'})_{A"}$
. We have
-
•
 $x_{A'} = 0$
unless
$x_{A'} = 0$
unless
 $A'\ge A$
since
$A'\ge A$
since
 $x\in X_{\ge A}$
.
$x\in X_{\ge A}$
. -
•
 $x_{A'} = 0$
unless
$x_{A'} = 0$
unless
 $A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
from the condition on x.
$A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
from the condition on x. -
•
 $f(x_{A'})_{A"} = 0$
unless
$f(x_{A'})_{A"} = 0$
unless
 $A"\ge A'$
from the definition of morphisms in
$A"\ge A'$
from the definition of morphisms in
 $\widetilde {\mathcal {K}}_P(S_0)$
.
$\widetilde {\mathcal {K}}_P(S_0)$
.
Therefore, in the sum
![]() $\sum _{A'\in \mathcal {A}}f(x_{A'})_{A"}$
, we may assume
$\sum _{A'\in \mathcal {A}}f(x_{A'})_{A"}$
, we may assume
![]() $A'$
satisfies
$A'$
satisfies
![]() $A\le A'\le A",A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. If
$A\le A'\le A",A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. If
![]() $A" = A$
, then
$A" = A$
, then
![]() $A\le A'\le A"$
, implying
$A\le A'\le A"$
, implying
![]() $A' = A$
. Hence,
$A' = A$
. Hence,
![]() $f(x)_A = f(x_A)_A$
. If
$f(x)_A = f(x_A)_A$
. If
![]() $A" = \alpha \uparrow A$
, we have
$A" = \alpha \uparrow A$
, we have
![]() $A\le A'\le \alpha \uparrow A$
and
$A\le A'\le \alpha \uparrow A$
and
![]() $A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. Thus, we have
$A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. Thus, we have
![]() $A' = A$
or
$A' = A$
or
![]() $\alpha \uparrow A$
. However, by Remark 2.7, we have
$\alpha \uparrow A$
. However, by Remark 2.7, we have
![]() $f(x_{A})_{\alpha \uparrow A} = 0$
. Hence,
$f(x_{A})_{\alpha \uparrow A} = 0$
. Hence,
![]() $f(x)_{\alpha \uparrow A} = f(x_{\alpha \uparrow A})_{\alpha \uparrow A}$
.
$f(x)_{\alpha \uparrow A} = f(x_{\alpha \uparrow A})_{\alpha \uparrow A}$
.
We prove (2). We have
![]() $f(x_{A'})\in \bigoplus _{A" \ge A'}Y_{A"}^{\emptyset }$
. Hence,
$f(x_{A'})\in \bigoplus _{A" \ge A'}Y_{A"}^{\emptyset }$
. Hence,
![]() $f(x_{A'}) - f(x_{A'})_{A'}\in \bigoplus _{A"> A'}Y_{A"}^{\emptyset }$
. Therefore,
$f(x_{A'}) - f(x_{A'})_{A'}\in \bigoplus _{A"> A'}Y_{A"}^{\emptyset }$
. Therefore,
![]() $g(f(x_{A'})) - g(f(x_{A'})_{A'})\in \bigoplus _{A"> A'}Z_{A"}^{\emptyset }$
. Hence,
$g(f(x_{A'})) - g(f(x_{A'})_{A'})\in \bigoplus _{A"> A'}Z_{A"}^{\emptyset }$
. Hence,
![]() $g(f(x_{A'}))_{A'} = g(f(x_{A'})_{A'})_{A'}$
. By (1), the right-hand side is
$g(f(x_{A'}))_{A'} = g(f(x_{A'})_{A'})_{A'}$
. By (1), the right-hand side is
![]() $g(f(x)_{A'})_{A'}$
and the left-hand side is
$g(f(x)_{A'})_{A'}$
and the left-hand side is
![]() $g(f(x_{A'}))_{A'} = (g\circ f)(x_{A'})_{A'} = (g\circ f)(x)_{A'} = g(f(x))_{A'}$
.
$g(f(x_{A'}))_{A'} = (g\circ f)(x_{A'})_{A'} = (g\circ f)(x)_{A'} = g(f(x))_{A'}$
.
Let
![]() $\varphi '\colon X'\to M^{\alpha }$
be another isomorphism which satisfies the condition for X and set
$\varphi '\colon X'\to M^{\alpha }$
be another isomorphism which satisfies the condition for X and set
![]() $\psi = (\varphi ')^{-1}\circ \varphi $
. For
$\psi = (\varphi ')^{-1}\circ \varphi $
. For
![]() $A'\in \{A,\alpha \uparrow A\}$
, we have
$A'\in \{A,\alpha \uparrow A\}$
, we have
![]() $\varphi (x_{A'})_{A'} = \varphi (x)_{A'} = \varphi '(\psi (x))_{A'} = \varphi '(\psi (x)_{A'})_{A'}$
. Hence,
$\varphi (x_{A'})_{A'} = \varphi (x)_{A'} = \varphi '(\psi (x))_{A'} = \varphi '(\psi (x)_{A'})_{A'}$
. Hence,
![]() $(\varphi (x_{A})_{A},\varphi (x_{\alpha \uparrow A})_{\alpha \uparrow A}) = (\varphi '(\psi (x)_{A})_{A},\varphi '(\psi (x)_{\alpha \uparrow A})_{\alpha \uparrow A})$
. As
$(\varphi (x_{A})_{A},\varphi (x_{\alpha \uparrow A})_{\alpha \uparrow A}) = (\varphi '(\psi (x)_{A})_{A},\varphi '(\psi (x)_{\alpha \uparrow A})_{\alpha \uparrow A})$
. As
![]() $\psi $
is a morphism,
$\psi $
is a morphism,
![]() $\psi (x)\in X^{\prime }_{\ge A}$
. Hence, the right-hand side is in
$\psi (x)\in X^{\prime }_{\ge A}$
. Hence, the right-hand side is in
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
determined by
$(\mathcal {F}(S_0)(M))(A,\alpha )$
determined by
![]() $X'$
. Therefore, the space
$X'$
. Therefore, the space
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
determined by X is contained in the space
$(\mathcal {F}(S_0)(M))(A,\alpha )$
determined by X is contained in the space
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
determined by
$(\mathcal {F}(S_0)(M))(A,\alpha )$
determined by
![]() $X'$
. By swapping X with
$X'$
. By swapping X with
![]() $X'$
, we get the reverse inclusion and therefore, the space
$X'$
, we get the reverse inclusion and therefore, the space
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
does not depend on the choice of X.
$(\mathcal {F}(S_0)(M))(A,\alpha )$
does not depend on the choice of X.
Let
![]() $f\colon M\to N$
be a morphism in
$f\colon M\to N$
be a morphism in
![]() $\mathcal {K}_P(S_0)$
and take a lift
$\mathcal {K}_P(S_0)$
and take a lift
![]() $\widetilde {f}\in \operatorname {\mathrm {Hom}}_{\widetilde {\mathcal {K}}_P(S_0)}(M,N)$
of f. Then, we have a homomorphism
$\widetilde {f}\in \operatorname {\mathrm {Hom}}_{\widetilde {\mathcal {K}}_P(S_0)}(M,N)$
of f. Then, we have a homomorphism
![]() $(\mathcal {F}(S_0)(f))(A)\colon M_A^{\emptyset }\to N_A^{\emptyset }$
defined by
$(\mathcal {F}(S_0)(f))(A)\colon M_A^{\emptyset }\to N_A^{\emptyset }$
defined by
![]() $M_A^{\emptyset }\hookrightarrow \bigoplus _{A'\ge A}M_{A'}^{\emptyset }\xrightarrow {\widetilde {f}}\bigoplus _{A'\ge A}N_{A'}^{\emptyset }\twoheadrightarrow N_{A}^{\emptyset }$
. In other words, we put
$M_A^{\emptyset }\hookrightarrow \bigoplus _{A'\ge A}M_{A'}^{\emptyset }\xrightarrow {\widetilde {f}}\bigoplus _{A'\ge A}N_{A'}^{\emptyset }\twoheadrightarrow N_{A}^{\emptyset }$
. In other words, we put
![]() $(\mathcal {F}(S_0)(f))(A)(m) = \widetilde {f}(m)_{A}$
. It is easy to see that this does not depend on a lift
$(\mathcal {F}(S_0)(f))(A)(m) = \widetilde {f}(m)_{A}$
. It is easy to see that this does not depend on a lift
![]() $\widetilde {f}$
.
$\widetilde {f}$
.
We prove that the collection
![]() $((\mathcal {F}(S_0)(f))(A))_{A\in \mathcal {A}}$
preserves
$((\mathcal {F}(S_0)(f))(A))_{A\in \mathcal {A}}$
preserves
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
. Take
$(\mathcal {F}(S_0)(M))(A,\alpha )$
. Take
![]() $X\in \widetilde {\mathcal {K}}_{P}(S_0^{\alpha })$
and
$X\in \widetilde {\mathcal {K}}_{P}(S_0^{\alpha })$
and
![]() $\varphi \colon X\xrightarrow {\sim } M^{\alpha }$
as in the definition of
$\varphi \colon X\xrightarrow {\sim } M^{\alpha }$
as in the definition of
![]() $(\mathcal {F}(S_0)(M))(A,\alpha )$
. We also take
$(\mathcal {F}(S_0)(M))(A,\alpha )$
. We also take
![]() $\psi \colon Y\xrightarrow {\sim } N^{\alpha }$
where
$\psi \colon Y\xrightarrow {\sim } N^{\alpha }$
where
![]() $Y\in \mathcal {K}_{P}(S_{0}^{\alpha })$
satisfies
$Y\in \mathcal {K}_{P}(S_{0}^{\alpha })$
satisfies
![]() $Y = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}}(Y\cap \bigoplus _{A\in \Omega } Y_{A}^{\emptyset })$
. Let
$Y = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}}(Y\cap \bigoplus _{A\in \Omega } Y_{A}^{\emptyset })$
. Let
![]() $(x_1,x_2)\in (\mathcal {F}(S_0)(M))(A,\alpha )$
. There exists
$(x_1,x_2)\in (\mathcal {F}(S_0)(M))(A,\alpha )$
. There exists
![]() $x\in X_{\ge A}$
such that
$x\in X_{\ge A}$
such that
![]() $(x_1,x_2) = (\varphi (x_A)_A,\varphi (x_{\alpha \uparrow A})_{\alpha \uparrow A})$
. We may assume
$(x_1,x_2) = (\varphi (x_A)_A,\varphi (x_{\alpha \uparrow A})_{\alpha \uparrow A})$
. We may assume
![]() $x\in \bigoplus _{A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A}X_{A'}^{\emptyset }$
. We put
$x\in \bigoplus _{A'\in W^{\prime }_{\alpha ,{\mathrm {aff}}}A}X_{A'}^{\emptyset }$
. We put
![]() $\widetilde {g} = \psi ^{-1}\circ \widetilde {f}$
. Then,
$\widetilde {g} = \psi ^{-1}\circ \widetilde {f}$
. Then,
![]() $(\mathcal {F}(S_0)(f))(A)(x_1) = \widetilde {f}(\varphi (x_A)_A)_A = \psi (\widetilde {g}(\varphi (x_A)_A))_A$
. By Lemma 3.13 (2) to
$(\mathcal {F}(S_0)(f))(A)(x_1) = \widetilde {f}(\varphi (x_A)_A)_A = \psi (\widetilde {g}(\varphi (x_A)_A))_A$
. By Lemma 3.13 (2) to
![]() $\varphi (x_A)_A$
, we have
$\varphi (x_A)_A$
, we have
![]() $\psi (\widetilde {g}(\varphi (x_A)_A))_A = \psi (\widetilde {g}(\varphi (x_A)_A)_A)_A$
and again by Lemma 3.13 (1), (2), this is equal to
$\psi (\widetilde {g}(\varphi (x_A)_A))_A = \psi (\widetilde {g}(\varphi (x_A)_A)_A)_A$
and again by Lemma 3.13 (1), (2), this is equal to
![]() $\psi (\widetilde {g}(\varphi (x))_{A})_A$
. Similarly, we have
$\psi (\widetilde {g}(\varphi (x))_{A})_A$
. Similarly, we have
![]() $(\mathcal {F}(S_0)(f))(\alpha \uparrow A)(x_2) = \psi (\widetilde {g}(\varphi (x))_{\alpha \uparrow A})_{\alpha \uparrow A}$
. Since the element
$(\mathcal {F}(S_0)(f))(\alpha \uparrow A)(x_2) = \psi (\widetilde {g}(\varphi (x))_{\alpha \uparrow A})_{\alpha \uparrow A}$
. Since the element
![]() $(\psi (\widetilde {g}(\varphi (x))_{A})_A,\psi (\widetilde {g}(\varphi (x))_{\alpha \uparrow A})_{\alpha \uparrow A})$
is the image of
$(\psi (\widetilde {g}(\varphi (x))_{A})_A,\psi (\widetilde {g}(\varphi (x))_{\alpha \uparrow A})_{\alpha \uparrow A})$
is the image of
![]() $\widetilde {g}(\varphi (x))\in Y_{\ge A}$
under
$\widetilde {g}(\varphi (x))\in Y_{\ge A}$
under
![]() $Y_{\ge A}\to Y_{A}^{\emptyset }\oplus Y_{\alpha \uparrow A}^{\emptyset }\simeq N_{A}^{\emptyset }\oplus N_{\alpha \uparrow A}^{\emptyset }$
, it is in
$Y_{\ge A}\to Y_{A}^{\emptyset }\oplus Y_{\alpha \uparrow A}^{\emptyset }\simeq N_{A}^{\emptyset }\oplus N_{\alpha \uparrow A}^{\emptyset }$
, it is in
![]() $(\mathcal {F}(S_0)(N))(A,\alpha )$
. Hence, we have proved that the collection
$(\mathcal {F}(S_0)(N))(A,\alpha )$
. Hence, we have proved that the collection
![]() $((\mathcal {F}(S_0)(f))(A))_{A\in \mathcal {A}}$
defines a morphism
$((\mathcal {F}(S_0)(f))(A))_{A\in \mathcal {A}}$
defines a morphism
![]() $\mathcal {F}(S_0)(M)\to \mathcal {F}(S_0)(N)$
. Hence,
$\mathcal {F}(S_0)(M)\to \mathcal {F}(S_0)(N)$
. Hence,
![]() $\mathcal {F}(S_0)$
is a functor.
$\mathcal {F}(S_0)$
is a functor.
Put
![]() $\mathcal {F} = \mathcal {F}(S)$
and
$\mathcal {F} = \mathcal {F}(S)$
and
![]() $\mathcal {F}^{*} = \mathcal {F}(S^*)$
for
$\mathcal {F}^{*} = \mathcal {F}(S^*)$
for
![]() $*\in \{\emptyset \}\cup \Delta $
.
$*\in \{\emptyset \}\cup \Delta $
.
Proposition 3.14. We have
![]() $\mathcal {F}(M*B_s)\simeq \vartheta _s(\mathcal {F}(M))$
.
$\mathcal {F}(M*B_s)\simeq \vartheta _s(\mathcal {F}(M))$
.
Proof. Before giving a proof, we give some notation. Fix
![]() $\alpha \in \Delta $
and
$\alpha \in \Delta $
and
![]() $M\in \mathcal {K}(S_0)$
. Put
$M\in \mathcal {K}(S_0)$
. Put
![]() $M^{(\Omega )} = M^{\alpha }\cap \bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
for
$M^{(\Omega )} = M^{\alpha }\cap \bigoplus _{A\in \Omega }M_{A}^{\emptyset }$
for
![]() $\Omega \in W_{\alpha ,{\mathrm {aff}}}'\backslash \mathcal {A}$
. Then, if
$\Omega \in W_{\alpha ,{\mathrm {aff}}}'\backslash \mathcal {A}$
. Then, if
![]() $M^{\alpha } = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(M^{\alpha }\cap \bigoplus _{A\in \Omega }M_{A}^{\emptyset })$
, then
$M^{\alpha } = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(M^{\alpha }\cap \bigoplus _{A\in \Omega }M_{A}^{\emptyset })$
, then
![]() $(\mathcal {F}(M))(A,\alpha )$
is the image of
$(\mathcal {F}(M))(A,\alpha )$
is the image of
![]() $M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}$
in
$M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}$
in
![]() $M_{A}^{\emptyset }\oplus M_{\alpha \uparrow A}^{\emptyset }$
. As
$M_{A}^{\emptyset }\oplus M_{\alpha \uparrow A}^{\emptyset }$
. As
![]() $\operatorname {\mathrm {supp}} M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
and
$\operatorname {\mathrm {supp}} M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}\subset W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
and
![]() $W^{\prime }_{\alpha ,{\mathrm {aff}}}\cap [A,\alpha \uparrow A] = \{A,\alpha \uparrow A\}$
, we have
$W^{\prime }_{\alpha ,{\mathrm {aff}}}\cap [A,\alpha \uparrow A] = \{A,\alpha \uparrow A\}$
, we have
![]() $(\mathcal {F}(M))(A,\alpha ) \simeq M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}_{[A,\alpha \uparrow A]}$
.
$(\mathcal {F}(M))(A,\alpha ) \simeq M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}_{[A,\alpha \uparrow A]}$
.
Take
![]() $\delta _s\in \Lambda ^\vee _{{\mathbb {K}}}$
such that
$\delta _s\in \Lambda ^\vee _{{\mathbb {K}}}$
such that
![]() $\langle \alpha _s,\delta _s\rangle = 1$
and put
$\langle \alpha _s,\delta _s\rangle = 1$
and put
![]() $b_e = (\alpha _s^\vee )^{-1}(\delta _s\otimes 1 - 1\otimes s(\delta _s))$
and
$b_e = (\alpha _s^\vee )^{-1}(\delta _s\otimes 1 - 1\otimes s(\delta _s))$
and
![]() $b_s = (\alpha _s^\vee )^{-1}(\delta _s\otimes 1 - 1\otimes \delta _s)$
. Note that this does not depend on a choice of
$b_s = (\alpha _s^\vee )^{-1}(\delta _s\otimes 1 - 1\otimes \delta _s)$
. Note that this does not depend on a choice of
![]() $\delta _s$
. We fix
$\delta _s$
. We fix
![]() $(B_s)_e^{\emptyset }\simeq R^{\emptyset }$
and
$(B_s)_e^{\emptyset }\simeq R^{\emptyset }$
and
![]() $(B_s)_s^{\emptyset }\simeq R^{\emptyset }$
as
$(B_s)_s^{\emptyset }\simeq R^{\emptyset }$
as
 $$ \begin{gather*} R^{\emptyset}\ni 1\mapsto b_e\in (B_s)_e^{\emptyset},\\ R^{\emptyset}\ni 1\mapsto b_s\in (B_s)_s^{\emptyset}. \end{gather*} $$
$$ \begin{gather*} R^{\emptyset}\ni 1\mapsto b_e\in (B_s)_e^{\emptyset},\\ R^{\emptyset}\ni 1\mapsto b_s\in (B_s)_s^{\emptyset}. \end{gather*} $$
We have
![]() $(M*B_s)_{A}^{\emptyset } = M_{A}^{\emptyset }\otimes (B_s)_e^{\emptyset }\oplus M_{As}^{\emptyset }\otimes (B_s)_s^{\emptyset }\simeq M_{A}^{\emptyset }\oplus M_{As}^{\emptyset } = \vartheta _s(\mathcal {F}(M))(A)$
. Here, we use the above fixed isomorphisms. We check
$(M*B_s)_{A}^{\emptyset } = M_{A}^{\emptyset }\otimes (B_s)_e^{\emptyset }\oplus M_{As}^{\emptyset }\otimes (B_s)_s^{\emptyset }\simeq M_{A}^{\emptyset }\oplus M_{As}^{\emptyset } = \vartheta _s(\mathcal {F}(M))(A)$
. Here, we use the above fixed isomorphisms. We check
![]() $\mathcal {F}(M*B_s)(A,\alpha ) \simeq \vartheta _s(\mathcal {F}(M))(A,\alpha )$
under this isomorphism. We may assume
$\mathcal {F}(M*B_s)(A,\alpha ) \simeq \vartheta _s(\mathcal {F}(M))(A,\alpha )$
under this isomorphism. We may assume
![]() $M^{\alpha } = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(M^{\alpha }\cap \bigoplus _{A\in \Omega }M_A^{\emptyset })$
.
$M^{\alpha } = \bigoplus _{\Omega \in W^{\prime }_{\alpha ,{\mathrm {aff}}}\backslash \mathcal {A}}(M^{\alpha }\cap \bigoplus _{A\in \Omega }M_A^{\emptyset })$
.
First, we assume that
![]() $As\notin W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. Then, we have
$As\notin W^{\prime }_{\alpha ,{\mathrm {aff}}}A$
. Then, we have
![]() $(M*B_s)^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)} = M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}\otimes b_e\oplus M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}As)}\otimes b_s$
by Lemma 2.23. As
$(M*B_s)^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)} = M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}\otimes b_e\oplus M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}As)}\otimes b_s$
by Lemma 2.23. As
![]() $b_e\in (B_s)_e^{\emptyset }$
(resp.
$b_e\in (B_s)_e^{\emptyset }$
(resp.
![]() $b_s\in (B_s)_s^{\emptyset }$
) and
$b_s\in (B_s)_s^{\emptyset }$
) and
![]() $[A,\alpha \uparrow A]s\cap W^{\prime }_{\alpha ,{\mathrm {aff}}}As = [As,\alpha \uparrow As]\cap W^{\prime }_{\alpha ,{\mathrm {aff}}}As$
, we have
$[A,\alpha \uparrow A]s\cap W^{\prime }_{\alpha ,{\mathrm {aff}}}As = [As,\alpha \uparrow As]\cap W^{\prime }_{\alpha ,{\mathrm {aff}}}As$
, we have
Therefore,
![]() $\mathcal {F}(M*B_s)(A,\alpha ) = \mathcal {F}(M)(A,\alpha )\oplus \mathcal {F}(M)(As,\alpha ) = \vartheta _s(\mathcal {F}(M))(A,\alpha )$
.
$\mathcal {F}(M*B_s)(A,\alpha ) = \mathcal {F}(M)(A,\alpha )\oplus \mathcal {F}(M)(As,\alpha ) = \vartheta _s(\mathcal {F}(M))(A,\alpha )$
.
Next, assume that
![]() $As = \alpha \uparrow A$
. Then, we have
$As = \alpha \uparrow A$
. Then, we have
![]() $[A,\alpha \uparrow A] = [A,As] = \{A,As\}$
. Hence,
$[A,\alpha \uparrow A] = [A,As] = \{A,As\}$
. Hence,
![]() $\mathcal {F}(M*B_s)(A,\alpha ) = (M*B_s)^{\alpha }_{\{A,As\}}$
. Since
$\mathcal {F}(M*B_s)(A,\alpha ) = (M*B_s)^{\alpha }_{\{A,As\}}$
. Since
![]() $[A,As] = \{A,As\}$
is s-invariant, by Lemma 2.25, we have
$[A,As] = \{A,As\}$
is s-invariant, by Lemma 2.25, we have
![]() $(M*B_s)^{\alpha }_{[A,As]}\simeq M_{[A,As]}^{\alpha }\otimes _{R} B_s = \mathcal {F}(M)(A,\alpha )\otimes _R B_s$
. Our claim is that the image of
$(M*B_s)^{\alpha }_{[A,As]}\simeq M_{[A,As]}^{\alpha }\otimes _{R} B_s = \mathcal {F}(M)(A,\alpha )\otimes _R B_s$
. Our claim is that the image of
![]() $M_{\{A,As\}}^{\alpha }\otimes _{R}B_s$
in
$M_{\{A,As\}}^{\alpha }\otimes _{R}B_s$
in
![]() $(M_{\{A,As\}}*B_s)^{\emptyset } \simeq (M_{A}^{\emptyset }\oplus M_{As}^{\emptyset })\oplus (M_{As}^{\emptyset }\oplus M_{A}^{\emptyset })$
is equal to
$(M_{\{A,As\}}*B_s)^{\emptyset } \simeq (M_{A}^{\emptyset }\oplus M_{As}^{\emptyset })\oplus (M_{As}^{\emptyset }\oplus M_{A}^{\emptyset })$
is equal to
![]() $\{(x,y)\in M^{\alpha }_{\{A,As\}}\mid x - y\in \alpha ^\vee M^{\alpha }_{\{A,As\}}\}$
. We write the image of
$\{(x,y)\in M^{\alpha }_{\{A,As\}}\mid x - y\in \alpha ^\vee M^{\alpha }_{\{A,As\}}\}$
. We write the image of
![]() $m\in M$
in
$m\in M$
in
![]() $M_{A'}^{\emptyset }$
by
$M_{A'}^{\emptyset }$
by
![]() $m_{A'}$
for
$m_{A'}$
for
![]() $A'\in \mathcal {A}$
. We have
$A'\in \mathcal {A}$
. We have
![]() $M_{\{A,As\}}^{\alpha }\otimes _{R}B_s = M_{\{A,As\}}^{\alpha }\otimes _{R^s}R$
and the image of
$M_{\{A,As\}}^{\alpha }\otimes _{R}B_s = M_{\{A,As\}}^{\alpha }\otimes _{R^s}R$
and the image of
![]() $m_1\otimes 1 + m_2\otimes \delta _s\in M_{\{A,As\}}^{\alpha }\otimes _{R^s}R$
in
$m_1\otimes 1 + m_2\otimes \delta _s\in M_{\{A,As\}}^{\alpha }\otimes _{R^s}R$
in
![]() $(M_{A}^{\emptyset }\oplus M_{As}^{\emptyset })\oplus (M_{As}^{\emptyset }\oplus M_{A}^{\emptyset })$
is
$(M_{A}^{\emptyset }\oplus M_{As}^{\emptyset })\oplus (M_{As}^{\emptyset }\oplus M_{A}^{\emptyset })$
is
Therefore, we have
 $$ \begin{align*} (m_{1,A} + \delta_s^Am_{2,A},m_{1,As} + \delta_s^Am_{2,As}) &- (m_{1,A} + s(\delta_s)^Am_{2,A},m_{1,As} + s(\delta_s)^Am_{2,As})\\ &\qquad\qquad\qquad\qquad\qquad\qquad\quad = (\alpha_s^\vee)^A(m_{2,A},m_{2,As}) \end{align*} $$
$$ \begin{align*} (m_{1,A} + \delta_s^Am_{2,A},m_{1,As} + \delta_s^Am_{2,As}) &- (m_{1,A} + s(\delta_s)^Am_{2,A},m_{1,As} + s(\delta_s)^Am_{2,As})\\ &\qquad\qquad\qquad\qquad\qquad\qquad\quad = (\alpha_s^\vee)^A(m_{2,A},m_{2,As}) \end{align*} $$
which is in
![]() $\alpha ^\vee M_{\{A,As\}}^{\alpha }$
since
$\alpha ^\vee M_{\{A,As\}}^{\alpha }$
since
![]() $(\alpha _s^\vee )^A \in \{\pm 1\}\alpha ^\vee $
. From this formula it is easy to see the reverse inclusion.
$(\alpha _s^\vee )^A \in \{\pm 1\}\alpha ^\vee $
. From this formula it is easy to see the reverse inclusion.
Finally, we assume that
![]() $As = \alpha \downarrow A$
. Note that
$As = \alpha \downarrow A$
. Note that
![]() $As < A < \alpha \uparrow A < (\alpha \uparrow A)s$
. Put
$As < A < \alpha \uparrow A < (\alpha \uparrow A)s$
. Put
![]() $N = M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}$
. We have
$N = M^{(W^{\prime }_{\alpha ,{\mathrm {aff}}}A)}$
. We have
![]() $\mathcal {F}(N*B_s)(A,\alpha ) \subset \mathcal {F}(N*B_{s})(A)\oplus \mathcal {F}(N*B_s)(\alpha \uparrow A) = (N_{As}^{\emptyset }\oplus N_{A}^{\emptyset })\oplus (N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset })$
. We describe the image of
$\mathcal {F}(N*B_s)(A,\alpha ) \subset \mathcal {F}(N*B_{s})(A)\oplus \mathcal {F}(N*B_s)(\alpha \uparrow A) = (N_{As}^{\emptyset }\oplus N_{A}^{\emptyset })\oplus (N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset })$
. We describe the image of
![]() $(N*B_s)_{[A,\alpha \uparrow A]}$
in
$(N*B_s)_{[A,\alpha \uparrow A]}$
in
![]() $(N_{As}^{\emptyset }\oplus N_{A}^{\emptyset })\oplus (N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset })$
, or equivalently the image of
$(N_{As}^{\emptyset }\oplus N_{A}^{\emptyset })\oplus (N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset })$
, or equivalently the image of
![]() $(N*B_s)_{I}$
where
$(N*B_s)_{I}$
where
![]() $I = \{A'\in \mathcal {A}\mid A'\ge As\}\setminus \{As\}$
.
$I = \{A'\in \mathcal {A}\mid A'\ge As\}\setminus \{As\}$
.
Set
![]() $I' = \{A'\in \mathcal {A}\mid A'\ge As\}$
. Then,
$I' = \{A'\in \mathcal {A}\mid A'\ge As\}$
. Then,
![]() $I'\supset I$
and
$I'\supset I$
and
![]() $I'$
is s-invariant. Hence,
$I'$
is s-invariant. Hence,
![]() $(N*B_s)_{I'} = N_{I'}\otimes B_s = N_{I'}\otimes _{R^s}R$
by Lemma 2.25. Consider the projection
$(N*B_s)_{I'} = N_{I'}\otimes B_s = N_{I'}\otimes _{R^s}R$
by Lemma 2.25. Consider the projection
 $(N*B_s)_{I'}\to (N*B_s)_{As}\oplus (N*B_s)_{A}\oplus (N*B_s)_{\alpha \uparrow A} = (N_{As}^{\emptyset }\oplus N_{A}^{\emptyset })\oplus (N_{A}^{\emptyset }\oplus N_{As}^{\emptyset })\oplus (N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset })$
. This is given by
$(N*B_s)_{I'}\to (N*B_s)_{As}\oplus (N*B_s)_{A}\oplus (N*B_s)_{\alpha \uparrow A} = (N_{As}^{\emptyset }\oplus N_{A}^{\emptyset })\oplus (N_{A}^{\emptyset }\oplus N_{As}^{\emptyset })\oplus (N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset })$
. This is given by

Any element in
![]() $N_{I'}\otimes _{R^s}R$
is written as
$N_{I'}\otimes _{R^s}R$
is written as
![]() $m_1\otimes 1 + m_2\otimes \delta _s$
for
$m_1\otimes 1 + m_2\otimes \delta _s$
for
![]() $m_1,m_2\in N_{I'}$
. It is in
$m_1,m_2\in N_{I'}$
. It is in
![]() $(N*B_s)_{I}$
if and only the projection to
$(N*B_s)_{I}$
if and only the projection to
![]() $(N*B_s)_{As}^{\emptyset } \simeq N_{As}^{\emptyset }\oplus N_{A}^{\emptyset }$
is zero. This projection is given by
$(N*B_s)_{As}^{\emptyset } \simeq N_{As}^{\emptyset }\oplus N_{A}^{\emptyset }$
is zero. This projection is given by
![]() $(m_{1,As} + s_\alpha (\delta _s^A)m_{2,As},m_{1,A} + s_\alpha (\delta _s^A) m_{2,A})$
. Hence, it is sufficient to prove that the image of
$(m_{1,As} + s_\alpha (\delta _s^A)m_{2,As},m_{1,A} + s_\alpha (\delta _s^A) m_{2,A})$
. Hence, it is sufficient to prove that the image of
in
![]() $(N*B_s)_{A}^{\emptyset }\oplus (N*B_s)_{\alpha \uparrow A}^{\emptyset } = N_{A}^{\emptyset }\oplus N_{As}^{\emptyset }\oplus N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset }$
is
$(N*B_s)_{A}^{\emptyset }\oplus (N*B_s)_{\alpha \uparrow A}^{\emptyset } = N_{A}^{\emptyset }\oplus N_{As}^{\emptyset }\oplus N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset }$
is
![]() $\alpha ^\vee N_{[As,A]}\oplus N_{[\alpha \uparrow A,(\alpha \uparrow A)s]}$
(note that
$\alpha ^\vee N_{[As,A]}\oplus N_{[\alpha \uparrow A,(\alpha \uparrow A)s]}$
(note that
![]() $A = \alpha \uparrow (As)$
and
$A = \alpha \uparrow (As)$
and
![]() $(\alpha \uparrow A)s = \alpha \uparrow (\alpha \uparrow A)$
).
$(\alpha \uparrow A)s = \alpha \uparrow (\alpha \uparrow A)$
).
The image of
![]() $m_1\otimes 1 + m_2\otimes \delta _s$
in
$m_1\otimes 1 + m_2\otimes \delta _s$
in
![]() $N_{A}^{\emptyset }\oplus N_{As}^{\emptyset }\oplus N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset }$
is given by
$N_{A}^{\emptyset }\oplus N_{As}^{\emptyset }\oplus N_{\alpha \uparrow A}^{\emptyset }\oplus N_{(\alpha \uparrow A)s}^{\emptyset }$
is given by
Define
![]() $\varepsilon \in \{\pm 1\}$
by
$\varepsilon \in \{\pm 1\}$
by
![]() $\alpha _s^A = \varepsilon \alpha $
. Since
$\alpha _s^A = \varepsilon \alpha $
. Since
![]() $m_{1,A} + s_{\alpha }(\delta _s^A)m_{2,A} = 0$
, we have
$m_{1,A} + s_{\alpha }(\delta _s^A)m_{2,A} = 0$
, we have
![]() $m_{1,A} + \delta _s^Am_{2,A} = (\delta _s^A - s_{\alpha }(\delta _s^A))m_{2,A} = \varepsilon \alpha ^\vee m_{2,A}$
. By the same argument, we have
$m_{1,A} + \delta _s^Am_{2,A} = (\delta _s^A - s_{\alpha }(\delta _s^A))m_{2,A} = \varepsilon \alpha ^\vee m_{2,A}$
. By the same argument, we have
![]() $m_{1,As} + \delta _s^Am_{2,As} = \varepsilon \alpha ^\vee m_{2,As}$
. Therefore,
$m_{1,As} + \delta _s^Am_{2,As} = \varepsilon \alpha ^\vee m_{2,As}$
. Therefore,
![]() $(m_{1,A} + \delta _s^Am_{2,A},m_{1,As} + \delta _s^Am_{2,As}) = \alpha ^\vee (\varepsilon m_{2,A},\varepsilon m_{2,As})\in \alpha ^\vee N_{[A,As]}^{\emptyset }$
. Therefore, the image is in
$(m_{1,A} + \delta _s^Am_{2,A},m_{1,As} + \delta _s^Am_{2,As}) = \alpha ^\vee (\varepsilon m_{2,A},\varepsilon m_{2,As})\in \alpha ^\vee N_{[A,As]}^{\emptyset }$
. Therefore, the image is in
![]() $\alpha ^\vee N_{[As,A]}\oplus N_{[\alpha \uparrow A,(\alpha \uparrow A)s]}$
.
$\alpha ^\vee N_{[As,A]}\oplus N_{[\alpha \uparrow A,(\alpha \uparrow A)s]}$
.
However, let
![]() $m^{\prime }_1\in N_{[As,A]}$
and
$m^{\prime }_1\in N_{[As,A]}$
and
![]() $m^{\prime }_2\in N_{[\alpha \uparrow A,(\alpha \uparrow A)s]}$
. Take a lift
$m^{\prime }_2\in N_{[\alpha \uparrow A,(\alpha \uparrow A)s]}$
. Take a lift
![]() $m_1\in N_{I'}$
(resp.
$m_1\in N_{I'}$
(resp.
![]() $m_2\in M_{I"}$
) of
$m_2\in M_{I"}$
) of
![]() $m^{\prime }_1$
(resp.
$m^{\prime }_1$
(resp.
![]() $m^{\prime }_2$
) where
$m^{\prime }_2$
) where
![]() $I" = \{A'\in A\mid A'\ge \alpha \uparrow A\}$
. Put
$I" = \{A'\in A\mid A'\ge \alpha \uparrow A\}$
. Put
![]() $n = m_2\otimes 1 + \varepsilon (m_1\otimes \delta _s - (s(\delta _s))^Am_1\otimes 1)$
. Then, since
$n = m_2\otimes 1 + \varepsilon (m_1\otimes \delta _s - (s(\delta _s))^Am_1\otimes 1)$
. Then, since
![]() $m_2\in M_{I"}$
,
$m_2\in M_{I"}$
,
![]() $m_{2,A} = 0$
,
$m_{2,A} = 0$
,
![]() $m_{2,As} = 0$
. Now it is straightforward to see
$m_{2,As} = 0$
. Now it is straightforward to see
![]() $n\in (M*B_s)_{I}$
and the image of n is
$n\in (M*B_s)_{I}$
and the image of n is
![]() $(\alpha ^\vee m^{\prime }_{1,A},\alpha ^\vee m^{\prime }_{1,As},m^{\prime }_{2,\alpha \uparrow A},m^{\prime }_{2,(\alpha \uparrow A)s})$
. We get the proposition.
$(\alpha ^\vee m^{\prime }_{1,A},\alpha ^\vee m^{\prime }_{1,As},m^{\prime }_{2,\alpha \uparrow A},m^{\prime }_{2,(\alpha \uparrow A)s})$
. We get the proposition.
3.5 Some calculations of homomorphisms
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain. In this subsection, we fix a flat commutative graded S-algebra
${\mathbb {K}}$
is a complete local Noetherian integral domain. In this subsection, we fix a flat commutative graded S-algebra
![]() $S_0$
. We define some morphisms as follows. These will be used only in this subsection. Let
$S_0$
. We define some morphisms as follows. These will be used only in this subsection. Let
![]() $A\in \mathcal {A}$
and
$A\in \mathcal {A}$
and
![]() $\alpha \in \Delta ^+$
.
$\alpha \in \Delta ^+$
.
 $$ \begin{gather*} i_0\colon Q_{A,\alpha}\to Q_{A,\alpha}\quad (f,g)\mapsto (0,\alpha^\vee g),\\ i_0^+\colon Q_{A,\alpha}\to Q_{\alpha\uparrow A,\alpha}\quad (f,g)\mapsto (g,f),\\ i_0^-\colon Q_{A,\alpha}\to Q_{\alpha\downarrow A,\alpha}\quad (f,g)\mapsto (0,\alpha^\vee f). \end{gather*} $$
$$ \begin{gather*} i_0\colon Q_{A,\alpha}\to Q_{A,\alpha}\quad (f,g)\mapsto (0,\alpha^\vee g),\\ i_0^+\colon Q_{A,\alpha}\to Q_{\alpha\uparrow A,\alpha}\quad (f,g)\mapsto (g,f),\\ i_0^-\colon Q_{A,\alpha}\to Q_{\alpha\downarrow A,\alpha}\quad (f,g)\mapsto (0,\alpha^\vee f). \end{gather*} $$
It is straightforward to see that these are morphisms in
![]() $\widetilde {\mathcal {K}}$
. We use the same letter for the images of these morphisms in
$\widetilde {\mathcal {K}}$
. We use the same letter for the images of these morphisms in
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Lemma 3.15. We have
![]() $\operatorname {\mathrm {End}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A,\alpha }) = \operatorname {\mathrm {End}}^{\bullet }_{\widetilde {\mathcal {K}}(S_0)}(S_0\otimes _{S}Q_{A,\alpha }) = S_0\operatorname {\mathrm {id}}\oplus S_0i_0$
.
$\operatorname {\mathrm {End}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A,\alpha }) = \operatorname {\mathrm {End}}^{\bullet }_{\widetilde {\mathcal {K}}(S_0)}(S_0\otimes _{S}Q_{A,\alpha }) = S_0\operatorname {\mathrm {id}}\oplus S_0i_0$
.
Proof. Put
![]() $M = S_0\otimes _{S}Q_{A,\alpha }$
. Note that
$M = S_0\otimes _{S}Q_{A,\alpha }$
. Note that
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(M) = \{A,\alpha \uparrow A\}$
. Let
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(M) = \{A,\alpha \uparrow A\}$
. Let
![]() $\varphi \in \operatorname {\mathrm {End}}_{\widetilde {\mathcal {K}}(S_0)}(S_0\otimes _{S}Q_{A,\alpha })$
. We have
$\varphi \in \operatorname {\mathrm {End}}_{\widetilde {\mathcal {K}}(S_0)}(S_0\otimes _{S}Q_{A,\alpha })$
. We have
![]() $\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'\in A + {\mathbb {Z}}\Delta }M_{A'}^{\emptyset } = M_{A}^{\emptyset }$
. By the same argument, we also have
$\varphi (M_{A}^{\emptyset })\subset \bigoplus _{A'\in A + {\mathbb {Z}}\Delta }M_{A'}^{\emptyset } = M_{A}^{\emptyset }$
. By the same argument, we also have
![]() $\varphi (M_{\alpha \uparrow A}^{\emptyset })\subset M_{\alpha \uparrow A}^{\emptyset }$
. Therefore,
$\varphi (M_{\alpha \uparrow A}^{\emptyset })\subset M_{\alpha \uparrow A}^{\emptyset }$
. Therefore,
![]() $\varphi $
preserves
$\varphi $
preserves
![]() $M_{A'}^{\emptyset }$
for any
$M_{A'}^{\emptyset }$
for any
![]() $A'\in \mathcal {A}$
. Hence, we get the first equality of the lemma.
$A'\in \mathcal {A}$
. Hence, we get the first equality of the lemma.
We prove
![]() $\varphi \in S_0\operatorname {\mathrm {id}} + S_0i_0$
. Since
$\varphi \in S_0\operatorname {\mathrm {id}} + S_0i_0$
. Since
![]() $\varphi $
preserves
$\varphi $
preserves
![]() $M_{A'}^{\emptyset }$
, we have
$M_{A'}^{\emptyset }$
, we have
![]() $\varphi (f,g) = (\varphi _1(f),\varphi _2(g))$
for some
$\varphi (f,g) = (\varphi _1(f),\varphi _2(g))$
for some
![]() $\varphi _1,\varphi _2\colon S_0^{\emptyset }\to S_0^{\emptyset }$
. Restricting to
$\varphi _1,\varphi _2\colon S_0^{\emptyset }\to S_0^{\emptyset }$
. Restricting to
![]() $\{(f,g)\in M\mid g = 0\} = \alpha ^\vee S_0\oplus 0$
,
$\{(f,g)\in M\mid g = 0\} = \alpha ^\vee S_0\oplus 0$
,
![]() $\varphi _1$
sends
$\varphi _1$
sends
![]() $\alpha ^\vee S_0$
to
$\alpha ^\vee S_0$
to
![]() $\alpha ^\vee S_0$
. Therefore, it is given by
$\alpha ^\vee S_0$
. Therefore, it is given by
![]() $\varphi _1(f) = cf$
for some
$\varphi _1(f) = cf$
for some
![]() $c\in S_{0}$
. Replacing
$c\in S_{0}$
. Replacing
![]() $\varphi $
with
$\varphi $
with
![]() $\varphi - c\operatorname {\mathrm {id}}$
, we may assume
$\varphi - c\operatorname {\mathrm {id}}$
, we may assume
![]() $\varphi _{1} = 0$
. The image of
$\varphi _{1} = 0$
. The image of
![]() $\varphi $
is contained in
$\varphi $
is contained in
![]() $\{(f,g)\in M\mid f = 0\} = 0\oplus \alpha ^\vee S_0$
. Hence,
$\{(f,g)\in M\mid f = 0\} = 0\oplus \alpha ^\vee S_0$
. Hence,
![]() $\varphi _2(g) = \alpha ^\vee dg$
for some
$\varphi _2(g) = \alpha ^\vee dg$
for some
![]() $d\in S_0$
and we have
$d\in S_0$
and we have
![]() $\varphi = di_0$
.
$\varphi = di_0$
.
Lemma 3.16. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A,\alpha },S_0\otimes _{S}Q_{\alpha \uparrow A,\alpha }) = S_0i_0^{+}$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A,\alpha },S_0\otimes _{S}Q_{\alpha \uparrow A,\alpha }) = S_0i_0^{+}$
.
Proof. Let
![]() $\varphi \colon S_0\otimes _{S}Q_{A,\alpha }\to S_0\otimes _{S}Q_{\alpha \uparrow A,\alpha }$
be a morphism in
$\varphi \colon S_0\otimes _{S}Q_{A,\alpha }\to S_0\otimes _{S}Q_{\alpha \uparrow A,\alpha }$
be a morphism in
![]() $\widetilde {\mathcal {K}}(S_0)$
. By a similar argument of the proof of Lemma 3.15,
$\widetilde {\mathcal {K}}(S_0)$
. By a similar argument of the proof of Lemma 3.15,
![]() $\varphi $
is given by
$\varphi $
is given by
![]() $\varphi (f,g) = (\varphi _1(g),\varphi _2(f))$
for
$\varphi (f,g) = (\varphi _1(g),\varphi _2(f))$
for
![]() $\varphi _i\colon S_0^{\emptyset }\to S_0^{\emptyset }$
such that
$\varphi _i\colon S_0^{\emptyset }\to S_0^{\emptyset }$
such that
![]() $\varphi _i(\alpha ^\vee S_0)\subset \alpha ^\vee S_0$
for
$\varphi _i(\alpha ^\vee S_0)\subset \alpha ^\vee S_0$
for
![]() $i = 1,2$
. Hence,
$i = 1,2$
. Hence,
![]() $\varphi _1(f) = cf$
for some
$\varphi _1(f) = cf$
for some
![]() $c\in S_0$
. It is clear that
$c\in S_0$
. It is clear that
![]() $\varphi - ci_0^{+}$
is zero as a morphism in
$\varphi - ci_0^{+}$
is zero as a morphism in
![]() $\mathcal {K}(S_0)$
. Hence, we get the lemma.
$\mathcal {K}(S_0)$
. Hence, we get the lemma.
Lemma 3.17. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A,\alpha },S_0\otimes _{S}Q_{\alpha \downarrow A,\alpha }) = S_0i_0^{-}$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A,\alpha },S_0\otimes _{S}Q_{\alpha \downarrow A,\alpha }) = S_0i_0^{-}$
.
Proof. Set
![]() $M = S_0\otimes _{S}Q_{A,\alpha }$
and
$M = S_0\otimes _{S}Q_{A,\alpha }$
and
![]() $N = S_0\otimes _{S}Q_{\alpha \downarrow A,\alpha }$
and let
$N = S_0\otimes _{S}Q_{\alpha \downarrow A,\alpha }$
and let
![]() $\varphi \colon M\to N$
be a morphism in
$\varphi \colon M\to N$
be a morphism in
![]() $\widetilde {\mathcal {K}}(S_0)$
. We have
$\widetilde {\mathcal {K}}(S_0)$
. We have
![]() $\varphi (M_{\alpha \uparrow A}^{\emptyset })\subset \bigoplus _{A' \ge \alpha \uparrow A}N_{A'}^{\emptyset } = 0$
and
$\varphi (M_{\alpha \uparrow A}^{\emptyset })\subset \bigoplus _{A' \ge \alpha \uparrow A}N_{A'}^{\emptyset } = 0$
and
![]() $\varphi (M_{A}^{\emptyset }) \subset \bigoplus _{A' \in A + {\mathbb {Z}}\Delta }N_{A'}^{\emptyset } = N_{A}^{\emptyset }$
. Hence
$\varphi (M_{A}^{\emptyset }) \subset \bigoplus _{A' \in A + {\mathbb {Z}}\Delta }N_{A'}^{\emptyset } = N_{A}^{\emptyset }$
. Hence
![]() $\varphi (f,g) = (0,\varphi _1(f))$
for some
$\varphi (f,g) = (0,\varphi _1(f))$
for some
![]() $\varphi _1\colon S_{0}^{\emptyset }\to S_{0}^{\emptyset }$
. For any
$\varphi _1\colon S_{0}^{\emptyset }\to S_{0}^{\emptyset }$
. For any
![]() $f\in S_0$
we have
$f\in S_0$
we have
![]() $\varphi (f,f) = (0,\varphi _1(f))\in N$
. Hence,
$\varphi (f,f) = (0,\varphi _1(f))\in N$
. Hence,
![]() $\varphi _1(f)\in \alpha ^\vee S_0$
. Therefore,
$\varphi _1(f)\in \alpha ^\vee S_0$
. Therefore,
![]() $\varphi _1(f) = c\alpha ^\vee f$
for some
$\varphi _1(f) = c\alpha ^\vee f$
for some
![]() $c\in S_0$
. Hence,
$c\in S_0$
. Hence,
![]() $\varphi = ci_0^{-}$
.
$\varphi = ci_0^{-}$
.
Lemma 3.18. If
![]() $A_1\ne \alpha \downarrow A_2,A_2,\alpha \uparrow A_2$
, then
$A_1\ne \alpha \downarrow A_2,A_2,\alpha \uparrow A_2$
, then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}(S_0)}(Q_{A_1,\alpha },Q_{A_2,\alpha }) = 0$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}(S_0)}(Q_{A_1,\alpha },Q_{A_2,\alpha }) = 0$
.
Proof. It follows from
![]() $\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_1,\alpha })\cap \operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_2,\alpha }) = \emptyset $
.
$\operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_1,\alpha })\cap \operatorname {\mathrm {supp}}_{\mathcal {A}}(Q_{A_2,\alpha }) = \emptyset $
.
Next, we calculate homomorphisms in
![]() $\mathcal {K}_{{\mathrm {AJS}}}$
. Set
$\mathcal {K}_{{\mathrm {AJS}}}$
. Set
![]() $\mathcal {Q}_{A,\alpha } = \mathcal {F}(Q_{A,\alpha })$
.
$\mathcal {Q}_{A,\alpha } = \mathcal {F}(Q_{A,\alpha })$
.
Lemma 3.19. The object
![]() $\mathcal {Q}_{A,\alpha }$
is given by
$\mathcal {Q}_{A,\alpha }$
is given by
 $$ \begin{gather*} \mathcal{Q}_{A,\alpha}(A') = \begin{cases} S^{\emptyset} & (A' = A,\alpha\uparrow A),\\ 0 & (\text{otherwise}), \end{cases}\\ \mathcal{Q}_{A,\alpha}(A',\beta) = \begin{cases} S^{\beta}\oplus 0 & (A' = A,\alpha\uparrow A,\ \beta\ne\alpha),\\ 0\oplus S^{\beta} & (\beta\uparrow A' = A,\alpha\uparrow A,\ \beta\ne\alpha),\\ \alpha^\vee S^{\alpha}\oplus 0 & (A' = \alpha\uparrow A,\ \beta = \alpha),\\ \{(f,g)\in (S^{\alpha})^2\mid f\equiv g\quad\pmod{\alpha^\vee}\} & (A' = A,\ \beta = \alpha),\\ 0\oplus S^{\alpha} & (A' = \alpha\downarrow A,\ \beta = \alpha),\\ 0 & (\text{otherwise}). \end{cases} \end{gather*} $$
$$ \begin{gather*} \mathcal{Q}_{A,\alpha}(A') = \begin{cases} S^{\emptyset} & (A' = A,\alpha\uparrow A),\\ 0 & (\text{otherwise}), \end{cases}\\ \mathcal{Q}_{A,\alpha}(A',\beta) = \begin{cases} S^{\beta}\oplus 0 & (A' = A,\alpha\uparrow A,\ \beta\ne\alpha),\\ 0\oplus S^{\beta} & (\beta\uparrow A' = A,\alpha\uparrow A,\ \beta\ne\alpha),\\ \alpha^\vee S^{\alpha}\oplus 0 & (A' = \alpha\uparrow A,\ \beta = \alpha),\\ \{(f,g)\in (S^{\alpha})^2\mid f\equiv g\quad\pmod{\alpha^\vee}\} & (A' = A,\ \beta = \alpha),\\ 0\oplus S^{\alpha} & (A' = \alpha\downarrow A,\ \beta = \alpha),\\ 0 & (\text{otherwise}). \end{cases} \end{gather*} $$
Proof. The formula of
![]() $\mathcal {Q}_{A,\alpha }(A)$
is obvious. If
$\mathcal {Q}_{A,\alpha }(A)$
is obvious. If
![]() $\beta \ne \alpha $
, then
$\beta \ne \alpha $
, then
![]() $S^{\beta }\otimes _{S}Q_{A,\alpha } = S^{\beta }\oplus S^{\beta }$
. Hence, the formula of
$S^{\beta }\otimes _{S}Q_{A,\alpha } = S^{\beta }\oplus S^{\beta }$
. Hence, the formula of
![]() $\mathcal {Q}_{A,\alpha }(A',\beta )$
with
$\mathcal {Q}_{A,\alpha }(A',\beta )$
with
![]() $\beta \ne \alpha $
follows. The other formulas follow from a direct calculation.
$\beta \ne \alpha $
follows. The other formulas follow from a direct calculation.
Set
![]() $\iota _0 = \mathcal {F}(i_0)$
,
$\iota _0 = \mathcal {F}(i_0)$
,
![]() $\iota _0^{+} = \mathcal {F}(i_0^{+})$
,
$\iota _0^{+} = \mathcal {F}(i_0^{+})$
,
![]() $\iota _0^{-} = \mathcal {F}(i_0^{-})$
. These morphisms are described as follows.
$\iota _0^{-} = \mathcal {F}(i_0^{-})$
. These morphisms are described as follows.
 $$ \begin{gather*} \iota_0\colon \mathcal{Q}_{A,\alpha}\to \mathcal{Q}_{A,\alpha}\quad (\iota_0)_{A} = 0,(\iota_0)_{\alpha\uparrow A} = \alpha \operatorname{\mathrm{id}},\\ \iota_0^{+}\colon \mathcal{Q}_{A,\alpha}\to \mathcal{Q}_{\alpha\uparrow A,\alpha} \quad (\iota_0^{+})_{A} = 0,(\iota_0^{+})_{\alpha\uparrow A} = \operatorname{\mathrm{id}},\\ \iota_0^{-}\colon \mathcal{Q}_{A,\alpha}\to \mathcal{Q}_{\alpha\downarrow A,\alpha} \quad (\iota_0^{-})_{A} = \alpha \operatorname{\mathrm{id}},(\iota_0^{-})_{\alpha\uparrow A} = 0. \end{gather*} $$
$$ \begin{gather*} \iota_0\colon \mathcal{Q}_{A,\alpha}\to \mathcal{Q}_{A,\alpha}\quad (\iota_0)_{A} = 0,(\iota_0)_{\alpha\uparrow A} = \alpha \operatorname{\mathrm{id}},\\ \iota_0^{+}\colon \mathcal{Q}_{A,\alpha}\to \mathcal{Q}_{\alpha\uparrow A,\alpha} \quad (\iota_0^{+})_{A} = 0,(\iota_0^{+})_{\alpha\uparrow A} = \operatorname{\mathrm{id}},\\ \iota_0^{-}\colon \mathcal{Q}_{A,\alpha}\to \mathcal{Q}_{\alpha\downarrow A,\alpha} \quad (\iota_0^{-})_{A} = \alpha \operatorname{\mathrm{id}},(\iota_0^{-})_{\alpha\uparrow A} = 0. \end{gather*} $$
Lemma 3.20. We have
![]() $\operatorname {\mathrm {End}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {Q}_{A,\alpha }) = S_0\operatorname {\mathrm {id}}\oplus S_0\iota _0$
.
$\operatorname {\mathrm {End}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {Q}_{A,\alpha }) = S_0\operatorname {\mathrm {id}}\oplus S_0\iota _0$
.
Proof. Set
![]() $\mathcal {M} = S_0\otimes _{S}\mathcal {Q}_{A,\alpha }$
and let
$\mathcal {M} = S_0\otimes _{S}\mathcal {Q}_{A,\alpha }$
and let
![]() $\varphi \colon \mathcal {M}\to \mathcal {M}$
be a morphism. Since
$\varphi \colon \mathcal {M}\to \mathcal {M}$
be a morphism. Since
![]() $\mathcal {M}(A') = 0$
for
$\mathcal {M}(A') = 0$
for
![]() $A'\ne A,\alpha \uparrow A$
, we have
$A'\ne A,\alpha \uparrow A$
, we have
![]() $\varphi _{A'} = 0$
for such
$\varphi _{A'} = 0$
for such
![]() $A'$
. The morphism
$A'$
. The morphism
![]() $\varphi $
preserves
$\varphi $
preserves
![]() $\mathcal {M}(\beta \downarrow A,\beta ) = 0\oplus S_0^{\beta }$
for any
$\mathcal {M}(\beta \downarrow A,\beta ) = 0\oplus S_0^{\beta }$
for any
![]() $\beta \in \Delta ^+$
. Hence,
$\beta \in \Delta ^+$
. Hence,
![]() $\varphi _A(S_0^{\beta })\subset S_0^{\beta }$
. Therefore,
$\varphi _A(S_0^{\beta })\subset S_0^{\beta }$
. Therefore,
![]() $\varphi _A(S_0)\subset S_0$
and hence,
$\varphi _A(S_0)\subset S_0$
and hence,
![]() $\varphi _A = c\operatorname {\mathrm {id}}$
for some
$\varphi _A = c\operatorname {\mathrm {id}}$
for some
![]() $c\in S_0$
. We also have
$c\in S_0$
. We also have
![]() $\varphi _{\alpha \uparrow A} = d\operatorname {\mathrm {id}}$
for some
$\varphi _{\alpha \uparrow A} = d\operatorname {\mathrm {id}}$
for some
![]() $d\in S_0$
.
$d\in S_0$
.
We prove
![]() $\varphi \in S_0\operatorname {\mathrm {id}} + S_0\iota _{0}$
. By replacing
$\varphi \in S_0\operatorname {\mathrm {id}} + S_0\iota _{0}$
. By replacing
![]() $\varphi $
with
$\varphi $
with
![]() $\varphi - c\operatorname {\mathrm {id}}$
, we may assume
$\varphi - c\operatorname {\mathrm {id}}$
, we may assume
![]() $\varphi _{A} = 0$
. We have
$\varphi _{A} = 0$
. We have
![]() $(\varphi _A(f),\varphi _{\alpha \uparrow A}(g))\in \mathcal {M}(A,\alpha )$
for any
$(\varphi _A(f),\varphi _{\alpha \uparrow A}(g))\in \mathcal {M}(A,\alpha )$
for any
![]() $(f,g)\in \mathcal {M}(A,\alpha )$
. Since
$(f,g)\in \mathcal {M}(A,\alpha )$
. Since
![]() $\varphi _A(f) = 0$
, we have
$\varphi _A(f) = 0$
, we have
![]() $\varphi _{\alpha \uparrow A}(g)\in \alpha ^\vee S_0^{\alpha }$
. Therefore,
$\varphi _{\alpha \uparrow A}(g)\in \alpha ^\vee S_0^{\alpha }$
. Therefore,
![]() $d\in \alpha ^\vee S_0^{\alpha }\cap S_0 = \alpha ^\vee S_0$
. We have
$d\in \alpha ^\vee S_0^{\alpha }\cap S_0 = \alpha ^\vee S_0$
. We have
![]() $\varphi = (d/\alpha ^\vee )\iota _0$
.
$\varphi = (d/\alpha ^\vee )\iota _0$
.
Lemma 3.21. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {Q}_{A,\alpha },S_0\otimes _{S}\mathcal {Q}_{\alpha \uparrow A,\alpha }) = S_0\iota _0^{+}$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {Q}_{A,\alpha },S_0\otimes _{S}\mathcal {Q}_{\alpha \uparrow A,\alpha }) = S_0\iota _0^{+}$
.
Proof. Set
![]() $\mathcal {M} = S_0\otimes _{S}\mathcal {Q}_{A,\alpha }$
and
$\mathcal {M} = S_0\otimes _{S}\mathcal {Q}_{A,\alpha }$
and
![]() $\mathcal {N} = S_0\otimes _{S}\mathcal {Q}_{\alpha \uparrow A,\alpha }$
. Let
$\mathcal {N} = S_0\otimes _{S}\mathcal {Q}_{\alpha \uparrow A,\alpha }$
. Let
![]() $\varphi \colon \mathcal {M}\to \mathcal {N}$
be a morphism. Then,
$\varphi \colon \mathcal {M}\to \mathcal {N}$
be a morphism. Then,
![]() $\varphi _{A'} = 0$
for
$\varphi _{A'} = 0$
for
![]() $A'\ne \alpha \uparrow A$
. For
$A'\ne \alpha \uparrow A$
. For
![]() $\beta \in \Delta ^+\setminus \{\alpha \}$
, since
$\beta \in \Delta ^+\setminus \{\alpha \}$
, since
![]() $\varphi $
sends
$\varphi $
sends
![]() $\mathcal {M}(\alpha \uparrow A,\beta ) = S_0^{\beta }\oplus 0$
to
$\mathcal {M}(\alpha \uparrow A,\beta ) = S_0^{\beta }\oplus 0$
to
![]() $\mathcal {N}(\alpha \uparrow A,\beta ) = S_0^{\beta }\oplus 0$
, we have
$\mathcal {N}(\alpha \uparrow A,\beta ) = S_0^{\beta }\oplus 0$
, we have
![]() $\varphi _{\alpha \uparrow A}(S_0^{\beta })\subset S_0^{\beta }$
. Since
$\varphi _{\alpha \uparrow A}(S_0^{\beta })\subset S_0^{\beta }$
. Since
![]() $\varphi $
sends
$\varphi $
sends
![]() $\mathcal {M}(A,\alpha )$
to
$\mathcal {M}(A,\alpha )$
to
![]() $\mathcal {N}(A,\alpha ) = 0\oplus S^{\alpha }$
,
$\mathcal {N}(A,\alpha ) = 0\oplus S^{\alpha }$
,
![]() $\varphi _{\alpha \uparrow A}(S^{\alpha })\subset S^{\alpha }$
. Hence,
$\varphi _{\alpha \uparrow A}(S^{\alpha })\subset S^{\alpha }$
. Hence,
![]() $\varphi _{\alpha \uparrow A} \in S_0\operatorname {\mathrm {id}}$
and we get the lemma.
$\varphi _{\alpha \uparrow A} \in S_0\operatorname {\mathrm {id}}$
and we get the lemma.
Lemma 3.22. We have
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {Q}_{A,\alpha },S_0\otimes _{S}\mathcal {Q}_{\alpha \downarrow A,\alpha }) = S_0i_0^{-}$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {Q}_{A,\alpha },S_0\otimes _{S}\mathcal {Q}_{\alpha \downarrow A,\alpha }) = S_0i_0^{-}$
.
Proof. Set
![]() $\mathcal {M} = S_0\otimes _{S}\mathcal {Q}_{A,\alpha }$
and
$\mathcal {M} = S_0\otimes _{S}\mathcal {Q}_{A,\alpha }$
and
![]() $\mathcal {N} = S_0\otimes _{S}\mathcal {Q}_{\alpha \downarrow A,\alpha }$
. Let
$\mathcal {N} = S_0\otimes _{S}\mathcal {Q}_{\alpha \downarrow A,\alpha }$
. Let
![]() $\varphi \colon \mathcal {M}\to \mathcal {N}$
be a morphism. Then,
$\varphi \colon \mathcal {M}\to \mathcal {N}$
be a morphism. Then,
![]() $\varphi _{A'} = 0$
for
$\varphi _{A'} = 0$
for
![]() $A'\ne A$
. For
$A'\ne A$
. For
![]() $\beta \in \Delta ^+\setminus \{\alpha \}$
,
$\beta \in \Delta ^+\setminus \{\alpha \}$
,
![]() $\varphi $
sends
$\varphi $
sends
![]() $\mathcal {M}(A,\beta ) = 0\oplus S_0^\beta $
to
$\mathcal {M}(A,\beta ) = 0\oplus S_0^\beta $
to
![]() $\mathcal {N}(A,\beta ) = S_0^{\beta }\oplus 0$
. Hence,
$\mathcal {N}(A,\beta ) = S_0^{\beta }\oplus 0$
. Hence,
![]() $\varphi _A(S_0^{\beta })\subset S_0^{\beta }$
. The morphism
$\varphi _A(S_0^{\beta })\subset S_0^{\beta }$
. The morphism
![]() $\varphi $
sends
$\varphi $
sends
![]() $\mathcal {M}(A,\alpha )$
to
$\mathcal {M}(A,\alpha )$
to
![]() $\mathcal {N}(A,\alpha ) = \alpha ^\vee S^{\alpha }\oplus 0$
. Hence,
$\mathcal {N}(A,\alpha ) = \alpha ^\vee S^{\alpha }\oplus 0$
. Hence,
![]() $\varphi _{A}(S_0^{\alpha })\subset \alpha ^\vee S_0^{\alpha }$
. Therefore,
$\varphi _{A}(S_0^{\alpha })\subset \alpha ^\vee S_0^{\alpha }$
. Therefore,
![]() $\varphi _A \in \alpha ^\vee S_0 \operatorname {\mathrm {id}}$
and we get the lemma.
$\varphi _A \in \alpha ^\vee S_0 \operatorname {\mathrm {id}}$
and we get the lemma.
Lemma 3.23. If
![]() $A_1\ne \alpha \downarrow A_2,A_2,\alpha \uparrow A_2$
, then
$A_1\ne \alpha \downarrow A_2,A_2,\alpha \uparrow A_2$
, then
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(\mathcal {Q}_{A_1,\alpha },\mathcal {Q}_{A_2,\alpha }) = 0$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(\mathcal {Q}_{A_1,\alpha },\mathcal {Q}_{A_2,\alpha }) = 0$
.
Proof. It follows from there is no A such that
![]() $\mathcal {Q}_{A_1,\alpha }(A) \ne 0$
and
$\mathcal {Q}_{A_1,\alpha }(A) \ne 0$
and
![]() $\mathcal {Q}_{A_2,\alpha }(A)\ne 0$
.
$\mathcal {Q}_{A_2,\alpha }(A)\ne 0$
.
Summarizing the calculations in this subsection, we get the following.
Lemma 3.24. The functor
![]() $\mathcal {F}^{\alpha } = \mathcal {F}(S^{\alpha })$
induces an isomorphism
$\mathcal {F}^{\alpha } = \mathcal {F}(S^{\alpha })$
induces an isomorphism
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A_1,\alpha },S_0\otimes _{S}Q_{A_2,\alpha })\xrightarrow {\sim }\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {F}^{\alpha }(Q_{A_1,\alpha }),S_0\otimes _{S}\mathcal {F}^{\alpha }(Q_{A_2,\alpha }))$
.
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}(S_0)}(S_0\otimes _{S}Q_{A_1,\alpha },S_0\otimes _{S}Q_{A_2,\alpha })\xrightarrow {\sim }\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_0)}(S_0\otimes _{S}\mathcal {F}^{\alpha }(Q_{A_1,\alpha }),S_0\otimes _{S}\mathcal {F}^{\alpha }(Q_{A_2,\alpha }))$
.
3.6 Equivalence
Assume that
![]() ${\mathbb {K}}$
is a complete local Noetherian integral domain.
${\mathbb {K}}$
is a complete local Noetherian integral domain.
Lemma 3.25. The functor
![]() $\mathcal {F}^{\alpha }\colon \mathcal {K}^{\alpha }_P\to \mathcal {K}^{\alpha }_{{\mathrm {AJS}}}$
is fully faithful for
$\mathcal {F}^{\alpha }\colon \mathcal {K}^{\alpha }_P\to \mathcal {K}^{\alpha }_{{\mathrm {AJS}}}$
is fully faithful for
![]() $\alpha \in \Delta $
.
$\alpha \in \Delta $
.
Proof. By Corollary 3.8 and Proposition 3.12, we may assume
![]() $M = Q^{\alpha }_{A_1,\alpha }$
and
$M = Q^{\alpha }_{A_1,\alpha }$
and
![]() $N = Q^{\alpha }_{A_2,\alpha }$
, where
$N = Q^{\alpha }_{A_2,\alpha }$
, where
![]() $A_1,A_2\in \mathcal {A}$
. Hence, the lemma follows from Lemma 3.24.
$A_1,A_2\in \mathcal {A}$
. Hence, the lemma follows from Lemma 3.24.
Proposition 3.26. The functor
![]() $\mathcal {F}\colon \mathcal {K}_P\to \mathcal {K}_{{\mathrm {AJS}}}$
is fully faithful.
$\mathcal {F}\colon \mathcal {K}_P\to \mathcal {K}_{{\mathrm {AJS}}}$
is fully faithful.
Proof. Let
![]() $M,N\in \mathcal {K}_{P}$
and we prove that
$M,N\in \mathcal {K}_{P}$
and we prove that
![]() $\mathcal {F}\colon \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P}(M,N)\to \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}}(\mathcal {F}(M),\mathcal {F}(N))$
is an isomorphism. By the diagram
$\mathcal {F}\colon \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P}(M,N)\to \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}}(\mathcal {F}(M),\mathcal {F}(N))$
is an isomorphism. By the diagram

![]() $\mathcal {F}$
is injective (the injectivity of two morphisms in the above diagram follows from the definitions).
$\mathcal {F}$
is injective (the injectivity of two morphisms in the above diagram follows from the definitions).
We prove that
![]() $\mathcal {F}$
is surjective. For
$\mathcal {F}$
is surjective. For
![]() $\nu \in X_{{\mathbb {K}}}$
, let
$\nu \in X_{{\mathbb {K}}}$
, let
![]() $S_{(\nu )}$
be the localization at the prime ideal
$S_{(\nu )}$
be the localization at the prime ideal
![]() $(\nu )\subset S$
. Since
$(\nu )\subset S$
. Since
![]() $\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P}(M,N)$
is graded free, we have
$\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_P}(M,N)$
is graded free, we have
![]() $\operatorname {\mathrm {Im}}(\mathcal {F}) = \bigcap _{\nu \in X_{{\mathbb {K}}}}S_{(\nu )}\otimes _{S}\operatorname {\mathrm {Im}}(\mathcal {F})$
. By Corollary 3.8, we have
$\operatorname {\mathrm {Im}}(\mathcal {F}) = \bigcap _{\nu \in X_{{\mathbb {K}}}}S_{(\nu )}\otimes _{S}\operatorname {\mathrm {Im}}(\mathcal {F})$
. By Corollary 3.8, we have
![]() $S_{(\nu )}\otimes _{S}\operatorname {\mathrm {Im}}(\mathcal {F}) = \operatorname {\mathrm {Im}}(\mathcal {F}(S_{(\nu )}))$
. Since any
$S_{(\nu )}\otimes _{S}\operatorname {\mathrm {Im}}(\mathcal {F}) = \operatorname {\mathrm {Im}}(\mathcal {F}(S_{(\nu )}))$
. Since any
![]() $S_{(\nu )}$
is an
$S_{(\nu )}$
is an
![]() $S^{\alpha }$
-algebra for some
$S^{\alpha }$
-algebra for some
![]() $\alpha \in \Delta $
, by Proposition 3.26, we have
$\alpha \in \Delta $
, by Proposition 3.26, we have
![]() $\operatorname {\mathrm {Im}}(\mathcal {F}(S_{(\nu )})) = \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_{(\nu )})}(\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}M),\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}N))$
. Therefore,
$\operatorname {\mathrm {Im}}(\mathcal {F}(S_{(\nu )})) = \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_{(\nu )})}(\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}M),\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}N))$
. Therefore,
![]() $\mathcal {F}$
is surjective since
$\mathcal {F}$
is surjective since
![]() $\bigcap _{\nu \in X_{{\mathbb {K}}}}\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_{(\nu )})}(\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}M),\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}N))\supset \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}}(\mathcal {F}(M),\mathcal {F}(N))$
.
$\bigcap _{\nu \in X_{{\mathbb {K}}}}\operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}(S_{(\nu )})}(\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}M),\mathcal {F}(S_{(\nu )})(S_{(\nu )}\otimes _{S}N))\supset \operatorname {\mathrm {Hom}}^{\bullet }_{\mathcal {K}_{{\mathrm {AJS}}}}(\mathcal {F}(M),\mathcal {F}(N))$
.
Set
![]() $\mathcal {Q}_{\lambda } = \mathcal {F}(Q_{\lambda })$
. Let
$\mathcal {Q}_{\lambda } = \mathcal {F}(Q_{\lambda })$
. Let
![]() $\mathcal {K}_{{\mathrm {AJS}},P}$
be the full subcategory of
$\mathcal {K}_{{\mathrm {AJS}},P}$
be the full subcategory of
![]() $\mathcal {K}_{{\mathrm {AJS}}}$
consisting of direct summands of direct sums of objects of a form
$\mathcal {K}_{{\mathrm {AJS}}}$
consisting of direct summands of direct sums of objects of a form
![]() $(\vartheta _{s_1}\circ \dotsm \circ \vartheta _{s_l})(\mathcal {Q}_{\lambda })(n)$
for
$(\vartheta _{s_1}\circ \dotsm \circ \vartheta _{s_l})(\mathcal {Q}_{\lambda })(n)$
for
![]() $s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
,
$s_1,\dots ,s_l\in S_{{\mathrm {aff}}}$
,
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
and
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
and
![]() $n\in {\mathbb {Z}}$
. By Proposition 3.14 and 3.26, we get the following theorem.
$n\in {\mathbb {Z}}$
. By Proposition 3.14 and 3.26, we get the following theorem.
Theorem 3.27. We have
![]() $\mathcal {K}_{P}\simeq \mathcal {K}_{{\mathrm {AJS}},P}$
. In particular, the category
$\mathcal {K}_{P}\simeq \mathcal {K}_{{\mathrm {AJS}},P}$
. In particular, the category
![]() ${\mathcal {S}\mathrm {Bimod}}$
acts on
${\mathcal {S}\mathrm {Bimod}}$
acts on
![]() $\mathcal {K}_{{\mathrm {AJS}},P}$
.
$\mathcal {K}_{{\mathrm {AJS}},P}$
.
3.7 Representation Theory
In this subsection, we assume that
![]() ${\mathbb {K}}$
is an algebraically closed field of
${\mathbb {K}}$
is an algebraically closed field of
![]() $p> h$
, where h is the Coxeter number. Let G be a connected reductive group over
$p> h$
, where h is the Coxeter number. Let G be a connected reductive group over
![]() ${\mathbb {K}}$
and T a maximal torus of G with the root datum
${\mathbb {K}}$
and T a maximal torus of G with the root datum
![]() $(X,\Delta ,X^\vee ,\Delta ^\vee )$
. The Lie algebra
$(X,\Delta ,X^\vee ,\Delta ^\vee )$
. The Lie algebra
![]() $\mathfrak {g}$
of G has a structure of a p-Lie algebra. Let
$\mathfrak {g}$
of G has a structure of a p-Lie algebra. Let
![]() $U^{[p]}(\mathfrak {g})$
be the restricted enveloping algebra. Let
$U^{[p]}(\mathfrak {g})$
be the restricted enveloping algebra. Let
![]() $\widehat {S}$
be the completion of S at the augmentation ideal. For
$\widehat {S}$
be the completion of S at the augmentation ideal. For
![]() $S_0 = \widehat {S}$
or
$S_0 = \widehat {S}$
or
![]() ${\mathbb {K}}$
, let
${\mathbb {K}}$
, let
![]() $\mathcal {C}_{S_0}$
be the category defined in [Reference Andersen, Jantzen and SoergelAJS94]. The category
$\mathcal {C}_{S_0}$
be the category defined in [Reference Andersen, Jantzen and SoergelAJS94]. The category
![]() $\mathcal {C}_{{\mathbb {K}}}$
is equivalent to the category of
$\mathcal {C}_{{\mathbb {K}}}$
is equivalent to the category of
![]() $G_1T$
-modules, where
$G_1T$
-modules, where
![]() $G_1$
is the kernel of the Frobenius morphism. Let
$G_1$
is the kernel of the Frobenius morphism. Let
![]() $Z_{S_0}(\lambda )\in \mathcal {C}_{S_0}$
be the baby Verma module with highest weight
$Z_{S_0}(\lambda )\in \mathcal {C}_{S_0}$
be the baby Verma module with highest weight
![]() $\lambda $
and
$\lambda $
and
![]() $P_{S_0}(\lambda )\in \mathcal {C}_{S_0}$
the indecomposable projective module such that
$P_{S_0}(\lambda )\in \mathcal {C}_{S_0}$
the indecomposable projective module such that
![]() ${\mathbb {K}}\otimes _{S_0}P_{S_0}(\lambda )$
is the projective cover of the irreducible module with highest weight
${\mathbb {K}}\otimes _{S_0}P_{S_0}(\lambda )$
is the projective cover of the irreducible module with highest weight
![]() $\lambda $
. Such objects exist by [Reference Andersen, Jantzen and SoergelAJS94, 4.19 Theorem] when
$\lambda $
. Such objects exist by [Reference Andersen, Jantzen and SoergelAJS94, 4.19 Theorem] when
![]() $S_0 = \widehat {S}$
.
$S_0 = \widehat {S}$
.
We fix an alcove
![]() $A_0\in \mathcal {A}$
and
$A_0\in \mathcal {A}$
and
![]() $\lambda _0\in X\cap (pA_0 - \rho )$
, where
$\lambda _0\in X\cap (pA_0 - \rho )$
, where
![]() $\rho $
is the half sum of positive roots and
$\rho $
is the half sum of positive roots and
![]() $pA_0 = \{pa\mid a\in A_0\}$
. For
$pA_0 = \{pa\mid a\in A_0\}$
. For
![]() $S_0 = \widehat {S}$
or
$S_0 = \widehat {S}$
or
![]() ${\mathbb {K}}$
, let
${\mathbb {K}}$
, let
![]() $\mathcal {C}_{S_0,0}$
be the full subcategory of
$\mathcal {C}_{S_0,0}$
be the full subcategory of
![]() $\mathcal {C}_{S_0}$
consisting of quotients of modules of a form
$\mathcal {C}_{S_0}$
consisting of quotients of modules of a form
![]() $\bigoplus _{w\in W^{\prime }_{{\mathrm {aff}}}}P_{S_0}(w\cdot _{p}\lambda _{0})^{n_{w}}$
where
$\bigoplus _{w\in W^{\prime }_{{\mathrm {aff}}}}P_{S_0}(w\cdot _{p}\lambda _{0})^{n_{w}}$
where
![]() $w\cdot _p \lambda _0 = pw((\lambda _0 + \rho )/p) - \rho $
and
$w\cdot _p \lambda _0 = pw((\lambda _0 + \rho )/p) - \rho $
and
![]() $n_w\in {\mathbb {Z}}_{\ge 0}$
. Then, the cateogory
$n_w\in {\mathbb {Z}}_{\ge 0}$
. Then, the cateogory
![]() $\mathcal {C}_{S_0,0}$
is a direct summand of
$\mathcal {C}_{S_0,0}$
is a direct summand of
![]() $\mathcal {C}_{S_0}$
. Let
$\mathcal {C}_{S_0}$
. Let
![]() $\operatorname {\mathrm {Proj}}(\mathcal {C}_{S_0,0}) = \{P\in \mathcal {C}_{S_0,0}\mid P \text { is projective}\}$
.
$\operatorname {\mathrm {Proj}}(\mathcal {C}_{S_0,0}) = \{P\in \mathcal {C}_{S_0,0}\mid P \text { is projective}\}$
.
Let
![]() $S_0$
be a flat commutative S-algebra which is not necessary graded. We consider the following object:
$S_0$
be a flat commutative S-algebra which is not necessary graded. We consider the following object:
![]() $\mathcal {M} = ((\mathcal {M}(A))_{A\in \mathcal {A}},(\mathcal {M}(A,\alpha ))_{A\in \mathcal {A},\alpha \in \Delta ^+})$
, where
$\mathcal {M} = ((\mathcal {M}(A))_{A\in \mathcal {A}},(\mathcal {M}(A,\alpha ))_{A\in \mathcal {A},\alpha \in \Delta ^+})$
, where
![]() $\mathcal {M}(A)$
is an
$\mathcal {M}(A)$
is an
![]() $(S_0)^{\emptyset }$
-module and
$(S_0)^{\emptyset }$
-module and
![]() $\mathcal {M}(A,\alpha )\subset \mathcal {M}(A)\oplus \mathcal {M}(\alpha \uparrow A)$
is a sub-
$\mathcal {M}(A,\alpha )\subset \mathcal {M}(A)\oplus \mathcal {M}(\alpha \uparrow A)$
is a sub-
![]() $(S_0)^{\alpha }$
-module (we consider usual modules, not graded ones). Let
$(S_0)^{\alpha }$
-module (we consider usual modules, not graded ones). Let
![]() $\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}(S_0)$
be the category of such objects. Starting from this, we can define the functor
$\mathcal {K}_{{\mathrm {AJS}}}^{\mathrm {f}}(S_0)$
be the category of such objects. Starting from this, we can define the functor
![]() $\vartheta _s$
and the category
$\vartheta _s$
and the category
![]() $\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S_0)$
in a similar way. Andersen-Jantzen-Soergel proved the following (see [Reference Andersen, Jantzen and SoergelAJS94, 9.4. Proposition] for the full faithfulness. For the essential surjectivity, see the discussion in [Reference Andersen, Jantzen and SoergelAJS94, 16.5]). We modified the functor using [Reference FiebigFie11, Theorem 6.1].
$\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S_0)$
in a similar way. Andersen-Jantzen-Soergel proved the following (see [Reference Andersen, Jantzen and SoergelAJS94, 9.4. Proposition] for the full faithfulness. For the essential surjectivity, see the discussion in [Reference Andersen, Jantzen and SoergelAJS94, 16.5]). We modified the functor using [Reference FiebigFie11, Theorem 6.1].
Theorem 3.28. There is an equivalence of the categories
![]() $\mathcal {V}\colon \operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})\xrightarrow {\sim } \mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})$
.
$\mathcal {V}\colon \operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})\xrightarrow {\sim } \mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})$
.
Note that the functor
![]() $\mathcal {V}$
is defined explicitly.
$\mathcal {V}$
is defined explicitly.
Let
![]() ${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
be the category defined as follows. The objects of
${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
be the category defined as follows. The objects of
![]() ${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
are the same as those of
${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
are the same as those of
![]() $\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
, and the space of homomorphism is defined by
$\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
, and the space of homomorphism is defined by
Lemma 3.29. We have
![]() ${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})\simeq \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
.
${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})\simeq \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
.
Proof. We consider the functor
![]() ${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})\to \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
defined by
${\mathbb {K}}\otimes _{\widehat {S}}\operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})\to \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
defined by
![]() $P\mapsto {\mathbb {K}}\otimes _{\widehat {S}}P$
. This is essentially surjective by [Reference Andersen, Jantzen and SoergelAJS94, 4.19 Theorem] and fully faithful by [Reference Andersen, Jantzen and SoergelAJS94, 3.3 Proposition].
$P\mapsto {\mathbb {K}}\otimes _{\widehat {S}}P$
. This is essentially surjective by [Reference Andersen, Jantzen and SoergelAJS94, 4.19 Theorem] and fully faithful by [Reference Andersen, Jantzen and SoergelAJS94, 3.3 Proposition].
We also define
![]() ${\mathbb {K}}\otimes _{\widehat {S}}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})$
and
${\mathbb {K}}\otimes _{\widehat {S}}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})$
and
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S)$
in the same way.
${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S)$
in the same way.
Lemma 3.30. We have the following.
-
(1) The category
 $\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S)$
is equivalent to the category defined as follows: the objects are the same as
$\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S)$
is equivalent to the category defined as follows: the objects are the same as
 $\mathcal {K}_{{\mathrm {AJS}},P}$
, and the space of homomorphisms is defined by
$\mathcal {K}_{{\mathrm {AJS}},P}$
, and the space of homomorphisms is defined by
 $\operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}} = \operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}},P}}^{\bullet }$
.
$\operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}} = \operatorname {\mathrm {Hom}}_{\mathcal {K}_{{\mathrm {AJS}},P}}^{\bullet }$
. -
(2) We have
 ${\mathbb {K}}\otimes _{\widehat {S}}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})\simeq {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S)$
.
${\mathbb {K}}\otimes _{\widehat {S}}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})\simeq {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(S)$
.
Proof. (1) is obvious.
For (2), define
![]() $\widehat {S}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}$
in the obvious way. It is sufficient to prove
$\widehat {S}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}$
in the obvious way. It is sufficient to prove
![]() $\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})\simeq \widehat {S}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}$
. The functor
$\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})\simeq \widehat {S}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}$
. The functor
![]() $F\colon \widehat {S}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}\to \mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}},P}(\widehat {S})$
is defined in an obvious way and it is fully faithful by [Reference Andersen, Jantzen and SoergelAJS94, 14.8 Lemma]. In particular, F sends an indecomposable object to an indecomposable object. We define the category
$F\colon \widehat {S}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}\to \mathcal {K}^{\mathrm {f}}_{{\mathrm {AJS}},P}(\widehat {S})$
is defined in an obvious way and it is fully faithful by [Reference Andersen, Jantzen and SoergelAJS94, 14.8 Lemma]. In particular, F sends an indecomposable object to an indecomposable object. We define the category
![]() $\mathcal {K}_{P}^{\mathrm {f}}$
as in (1). Namely, the objects of
$\mathcal {K}_{P}^{\mathrm {f}}$
as in (1). Namely, the objects of
![]() $\mathcal {K}_{P}^{\mathrm {f}}$
are the same as those of
$\mathcal {K}_{P}^{\mathrm {f}}$
are the same as those of
![]() $\mathcal {K}_{P}^{\mathrm {f}}$
and we define
$\mathcal {K}_{P}^{\mathrm {f}}$
and we define
![]() $\operatorname {\mathrm {Hom}}_{\mathcal {K}_{P}^{\mathrm {f}}} = \operatorname {\mathrm {Hom}}_{\mathcal {K}_{P}}^{\bullet }$
. The indecomposable objects in
$\operatorname {\mathrm {Hom}}_{\mathcal {K}_{P}^{\mathrm {f}}} = \operatorname {\mathrm {Hom}}_{\mathcal {K}_{P}}^{\bullet }$
. The indecomposable objects in
![]() $\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}\simeq \mathcal {K}_{P}^{\mathrm {f}}$
and
$\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}\simeq \mathcal {K}_{P}^{\mathrm {f}}$
and
![]() $\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})\simeq \operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
are both parametrized by
$\mathcal {K}_{{\mathrm {AJS}},P}^{\mathrm {f}}(\widehat {S})\simeq \operatorname {\mathrm {Proj}}(\mathcal {C}_{\widehat {S},0})$
are both parametrized by
![]() $\mathcal {A}$
, and it is easy to see that F gives a bijection between the set of indecomposable objects. Therefore, F is essentially surjective.
$\mathcal {A}$
, and it is easy to see that F gives a bijection between the set of indecomposable objects. Therefore, F is essentially surjective.
Therefore, we get
Since the action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\mathcal {K}_{P}$
is S-linear, it gives an action on
$\mathcal {K}_{P}$
is S-linear, it gives an action on
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}^{\mathrm {f}}$
. Hence,
${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}^{\mathrm {f}}$
. Hence,
![]() ${\mathcal {S}\mathrm {Bimod}}$
acts on
${\mathcal {S}\mathrm {Bimod}}$
acts on
![]() $\operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
. With respect to this action,
$\operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
. With respect to this action,
![]() $B_s$
acts as the wall-crossing functor. We write this action as
$B_s$
acts as the wall-crossing functor. We write this action as
![]() $(M,B)\mapsto M*B$
.
$(M,B)\mapsto M*B$
.
Now we prove the following theorem.
Theorem 3.31. There is an action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\mathcal {C}_{{\mathbb {K}},0}$
such that
$\mathcal {C}_{{\mathbb {K}},0}$
such that
![]() $B_s$
acts as the wall-crossing functor for
$B_s$
acts as the wall-crossing functor for
![]() $s\in S_{\mathrm {aff}}$
.
$s\in S_{\mathrm {aff}}$
.
Let
![]() $L(p\lambda )\in \mathcal {C}_{{\mathbb {K}}}$
be the irreducible module with highest weight
$L(p\lambda )\in \mathcal {C}_{{\mathbb {K}}}$
be the irreducible module with highest weight
![]() $p\lambda $
for
$p\lambda $
for
![]() $\lambda \in {\mathbb {Z}}\Delta $
. The category
$\lambda \in {\mathbb {Z}}\Delta $
. The category
![]() $\mathcal {C}_{{\mathbb {K}},0}$
has the structure of
$\mathcal {C}_{{\mathbb {K}},0}$
has the structure of
![]() ${\mathbb {Z}}\Delta $
-category via
${\mathbb {Z}}\Delta $
-category via
![]() $M\mapsto M\otimes L(p\lambda )$
for
$M\mapsto M\otimes L(p\lambda )$
for
![]() $\lambda \in {\mathbb {Z}}\Delta $
. Fix a projective
$\lambda \in {\mathbb {Z}}\Delta $
. Fix a projective
![]() ${\mathbb {Z}}\Delta $
-generator P of
${\mathbb {Z}}\Delta $
-generator P of
![]() $\mathcal {C}_{{\mathbb {K}},0}$
and set
$\mathcal {C}_{{\mathbb {K}},0}$
and set
![]() $\mathcal {E} = \bigoplus _{\lambda \in {\mathbb {Z}}\Delta }\operatorname {\mathrm {Hom}}_{\mathcal {C}_{{\mathbb {K}},0}}(P,P\otimes L(p\lambda ))$
. This is a
$\mathcal {E} = \bigoplus _{\lambda \in {\mathbb {Z}}\Delta }\operatorname {\mathrm {Hom}}_{\mathcal {C}_{{\mathbb {K}},0}}(P,P\otimes L(p\lambda ))$
. This is a
![]() ${\mathbb {Z}}\Delta $
-graded algebra, and
${\mathbb {Z}}\Delta $
-graded algebra, and
![]() $\mathcal {C}_{{\mathbb {K}},0}\ni M\mapsto \bigoplus _{\lambda \in {\mathbb {Z}}\Delta }\operatorname {\mathrm {Hom}}(P,M\otimes L(p\lambda ))$
gives an equivalence of categories between
$\mathcal {C}_{{\mathbb {K}},0}\ni M\mapsto \bigoplus _{\lambda \in {\mathbb {Z}}\Delta }\operatorname {\mathrm {Hom}}(P,M\otimes L(p\lambda ))$
gives an equivalence of categories between
![]() $\mathcal {C}_{{\mathbb {K}},0}$
and the category of finitely generated
$\mathcal {C}_{{\mathbb {K}},0}$
and the category of finitely generated
![]() ${\mathbb {Z}}\Delta $
-graded right
${\mathbb {Z}}\Delta $
-graded right
![]() $\mathcal {E}$
-modules [Reference Andersen, Jantzen and SoergelAJS94, E.4 Proposition]. Let
$\mathcal {E}$
-modules [Reference Andersen, Jantzen and SoergelAJS94, E.4 Proposition]. Let
![]() $\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
be the the category of finitely generated
$\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
be the the category of finitely generated
![]() ${\mathbb {Z}}\Delta $
-graded right
${\mathbb {Z}}\Delta $
-graded right
![]() $\mathcal {E}$
-modules and
$\mathcal {E}$
-modules and
![]() $\operatorname {\mathrm {Proj}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
the category of projective objects in
$\operatorname {\mathrm {Proj}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
the category of projective objects in
![]() $\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
.
$\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
.
Lemma 3.32. We have
![]() $(Q*B)\otimes L(p\lambda )\simeq (Q\otimes L(p\lambda ))*B$
for
$(Q*B)\otimes L(p\lambda )\simeq (Q\otimes L(p\lambda ))*B$
for
![]() $Q\in \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
,
$Q\in \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
,
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
and
$B\in {\mathcal {S}\mathrm {Bimod}}$
and
![]() $\lambda \in {\mathbb {Z}}\Delta $
.
$\lambda \in {\mathbb {Z}}\Delta $
.
Proof. Let
![]() $\lambda \in {\mathbb {Z}}\Delta $
. Then, we have a functor
$\lambda \in {\mathbb {Z}}\Delta $
. Then, we have a functor
![]() $T_\lambda $
(resp.
$T_\lambda $
(resp.
![]() $T_{{\mathrm {AJS}},\lambda }$
) on
$T_{{\mathrm {AJS}},\lambda }$
) on
![]() $\mathcal {K}_P$
(resp.
$\mathcal {K}_P$
(resp.
![]() $\mathcal {K}_{{\mathrm {AJS}},P}$
) defined as follows.
$\mathcal {K}_{{\mathrm {AJS}},P}$
) defined as follows.
-
• For
 $M\in \mathcal {K}_P$
,
$M\in \mathcal {K}_P$
,
 $T_{\lambda }(M) = M$
and
$T_{\lambda }(M) = M$
and
 $T_{\lambda }(M)^{\emptyset }_{A} = M^{\emptyset }_{A + \lambda }$
.
$T_{\lambda }(M)^{\emptyset }_{A} = M^{\emptyset }_{A + \lambda }$
. -
• For
 $\mathcal {M}\in \mathcal {K}_{{\mathrm {AJS}}}$
,
$\mathcal {M}\in \mathcal {K}_{{\mathrm {AJS}}}$
,
 $T_{{\mathrm {AJS}},\lambda }(\mathcal {M})(A) = \mathcal {M}(A + \lambda )$
and
$T_{{\mathrm {AJS}},\lambda }(\mathcal {M})(A) = \mathcal {M}(A + \lambda )$
and
 $T_{{\mathrm {AJS}},\lambda }(\mathcal {M})(A,\alpha ) = \mathcal {M}(A + \lambda ,\alpha )$
.
$T_{{\mathrm {AJS}},\lambda }(\mathcal {M})(A,\alpha ) = \mathcal {M}(A + \lambda ,\alpha )$
.
Since these functors are S-linear, they give functors on
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}$
and
${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}$
and
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}$
, respectively. These functors give structures of
${\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}$
, respectively. These functors give structures of
![]() ${\mathbb {Z}}\Delta $
-category on each category. It is easy to see that equivalences
${\mathbb {Z}}\Delta $
-category on each category. It is easy to see that equivalences
![]() ${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}\simeq {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}\simeq \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
are
${\mathbb {K}}\otimes _{S}\mathcal {K}_{P}\simeq {\mathbb {K}}\otimes _{S}\mathcal {K}_{{\mathrm {AJS}},P}\simeq \operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
are
![]() ${\mathbb {Z}}\Delta $
-functor. Therefore, it is sufficient to prove
${\mathbb {Z}}\Delta $
-functor. Therefore, it is sufficient to prove
![]() $T_{\lambda }(M*B)\simeq T_{\lambda }(M)*B$
for
$T_{\lambda }(M*B)\simeq T_{\lambda }(M)*B$
for
![]() $M\in \mathcal {K}_{P}$
and
$M\in \mathcal {K}_{P}$
and
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
. This follows from the definition.
$B\in {\mathcal {S}\mathrm {Bimod}}$
. This follows from the definition.
Therefore, the action of
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
on
$B\in {\mathcal {S}\mathrm {Bimod}}$
on
![]() $\operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
is compatible with the
$\operatorname {\mathrm {Proj}}(\mathcal {C}_{{\mathbb {K}},0})$
is compatible with the
![]() ${\mathbb {Z}}\Delta $
-category structure, and it gives an action on
${\mathbb {Z}}\Delta $
-category structure, and it gives an action on
![]() $\operatorname {\mathrm {Proj}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
. We write this action again by
$\operatorname {\mathrm {Proj}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
. We write this action again by
![]() $M\mapsto M*B$
. For each
$M\mapsto M*B$
. For each
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
, we define
$B\in {\mathcal {S}\mathrm {Bimod}}$
, we define
![]() $\mathcal {E}(B)$
by
$\mathcal {E}(B)$
by
![]() $\mathcal {E}(B) = \bigoplus _{\lambda \in {\mathbb {Z}}\Delta }\operatorname {\mathrm {Hom}}(P,(P*B)\otimes L(p\lambda ))$
. This is a
$\mathcal {E}(B) = \bigoplus _{\lambda \in {\mathbb {Z}}\Delta }\operatorname {\mathrm {Hom}}(P,(P*B)\otimes L(p\lambda ))$
. This is a
![]() ${\mathbb {Z}}\Delta $
-graded
${\mathbb {Z}}\Delta $
-graded
![]() $\mathcal {E}$
-bimodule.
$\mathcal {E}$
-bimodule.
Lemma 3.33. Let Q be a projective finitely generated
![]() ${\mathbb {Z}}\Delta $
-graded
${\mathbb {Z}}\Delta $
-graded
![]() $\mathcal {E}$
-module. Then,
$\mathcal {E}$
-module. Then,
![]() $Q\otimes _{\mathcal {E}}\mathcal {E}(B)\simeq Q*B$
.
$Q\otimes _{\mathcal {E}}\mathcal {E}(B)\simeq Q*B$
.
Proof. Let
![]() $Q_{\nu }$
be the
$Q_{\nu }$
be the
![]() $\nu $
-th graded piece of Q, where
$\nu $
-th graded piece of Q, where
![]() $\nu \in {\mathbb {Z}}\Delta $
. Let
$\nu \in {\mathbb {Z}}\Delta $
. Let
![]() $p\in Q_{\nu }$
and let
$p\in Q_{\nu }$
and let
![]() $\varphi _{p}$
be the corresponding element in
$\varphi _{p}$
be the corresponding element in
![]() $\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})}(\mathcal {E},Q(\nu ))$
. Here
$\operatorname {\mathrm {Hom}}_{\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})}(\mathcal {E},Q(\nu ))$
. Here
![]() $(\nu )$
is the shift of the grading. Then,
$(\nu )$
is the shift of the grading. Then,
![]() $\varphi _p*B$
gives
$\varphi _p*B$
gives
![]() $\mathcal {E}*B\to Q(\nu )*B$
. By the definition,
$\mathcal {E}*B\to Q(\nu )*B$
. By the definition,
![]() $\mathcal {E}*B = \mathcal {E}(B)$
. Therefore, for
$\mathcal {E}*B = \mathcal {E}(B)$
. Therefore, for
![]() $m\in \mathcal {E}(B)$
, we have
$m\in \mathcal {E}(B)$
, we have
![]() $\varphi _p(m)\in Q(\nu )*B \simeq (Q*B)(\nu )$
. Hence, we get
$\varphi _p(m)\in Q(\nu )*B \simeq (Q*B)(\nu )$
. Hence, we get
![]() $Q\otimes _{\mathcal {E}}\mathcal {E}(B)\to Q*B$
by
$Q\otimes _{\mathcal {E}}\mathcal {E}(B)\to Q*B$
by
![]() $p\otimes m\mapsto \varphi _p(m)$
. This is an isomorphism if
$p\otimes m\mapsto \varphi _p(m)$
. This is an isomorphism if
![]() $Q = \mathcal {E}$
. Hence, it is an isomorphism for any
$Q = \mathcal {E}$
. Hence, it is an isomorphism for any
![]() $Q\in \operatorname {\mathrm {Proj}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
.
$Q\in \operatorname {\mathrm {Proj}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
.
Now for
![]() ${\mathbb {Z}}\Delta $
-graded right
${\mathbb {Z}}\Delta $
-graded right
![]() $\mathcal {E}$
-module M, put
$\mathcal {E}$
-module M, put
![]() $M*B = M\otimes _{\mathcal {E}}\mathcal {E}(B)$
. By the above lemma,
$M*B = M\otimes _{\mathcal {E}}\mathcal {E}(B)$
. By the above lemma,
![]() $\mathcal {E}(B_1)\otimes _{\mathcal {E}}\mathcal {E}(B_2)\simeq \mathcal {E}*B_1*B_2 = \mathcal {E}*(B_1\otimes B_2)\simeq \mathcal {E}(B_1\otimes B_2)$
. Hence,
$\mathcal {E}(B_1)\otimes _{\mathcal {E}}\mathcal {E}(B_2)\simeq \mathcal {E}*B_1*B_2 = \mathcal {E}*(B_1\otimes B_2)\simeq \mathcal {E}(B_1\otimes B_2)$
. Hence,
![]() $(M * B_1)*B_2 = (M\otimes _{\mathcal {E}}\mathcal {E}(B_1))\otimes _{\mathcal {E}}\mathcal {E}(B_2)\simeq M\otimes _{\mathcal {E}}(\mathcal {E}(B_1)\otimes _{\mathcal {E}}\mathcal {E}(B_2))\simeq M\otimes _{\mathcal {E}}\mathcal {E}(B_1\otimes B_2) = M*(B_1\otimes B_2)$
. It is easy to see that this gives an action of
$(M * B_1)*B_2 = (M\otimes _{\mathcal {E}}\mathcal {E}(B_1))\otimes _{\mathcal {E}}\mathcal {E}(B_2)\simeq M\otimes _{\mathcal {E}}(\mathcal {E}(B_1)\otimes _{\mathcal {E}}\mathcal {E}(B_2))\simeq M\otimes _{\mathcal {E}}\mathcal {E}(B_1\otimes B_2) = M*(B_1\otimes B_2)$
. It is easy to see that this gives an action of
![]() ${\mathcal {S}\mathrm {Bimod}}$
on
${\mathcal {S}\mathrm {Bimod}}$
on
![]() $\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
and therefore, on
$\operatorname {\mathrm {Mod}}_{{\mathbb {Z}}\Delta }(\mathcal {E})$
and therefore, on
![]() $\mathcal {C}_{{\mathbb {K}},0}$
.
$\mathcal {C}_{{\mathbb {K}},0}$
.
3.8 Characters
Assume that
![]() ${\mathbb {K}}$
is an algebraically closed field of
${\mathbb {K}}$
is an algebraically closed field of
![]() $p> h$
, where h is the Coxeter number. Any object
$p> h$
, where h is the Coxeter number. Any object
![]() $P\in \operatorname {\mathrm {Proj}}(\mathcal {C}_{S,0})$
has a baby Verma flag. Let
$P\in \operatorname {\mathrm {Proj}}(\mathcal {C}_{S,0})$
has a baby Verma flag. Let
![]() $(P:Z_{S}(w\cdot _p\lambda _0))$
be the the multiplicity of
$(P:Z_{S}(w\cdot _p\lambda _0))$
be the the multiplicity of
![]() $Z_{S}(w\cdot _{p}\lambda _0)$
in P. The following lemma is obvious from the constructions.
$Z_{S}(w\cdot _{p}\lambda _0)$
in P. The following lemma is obvious from the constructions.
Lemma 3.34. Let
![]() $P\in \operatorname {\mathrm {Proj}}(\mathcal {C}_{S,0})$
and
$P\in \operatorname {\mathrm {Proj}}(\mathcal {C}_{S,0})$
and
![]() $M\in \mathcal {K}_{P}$
such that
$M\in \mathcal {K}_{P}$
such that
![]() $\mathcal {V}(P)\simeq \mathcal {F}(M)$
. Then, we have
$\mathcal {V}(P)\simeq \mathcal {F}(M)$
. Then, we have
![]() $(P:Z_{S}(w\cdot _p\lambda _0)) = \operatorname {\mathrm {rank}}(M_{\{wA_0\}})$
for
$(P:Z_{S}(w\cdot _p\lambda _0)) = \operatorname {\mathrm {rank}}(M_{\{wA_0\}})$
for
![]() $w\in W^{\prime }_{{\mathrm {aff}}}$
.
$w\in W^{\prime }_{{\mathrm {aff}}}$
.
The projective module
![]() $P_S(\lambda )$
is characterized by
$P_S(\lambda )$
is characterized by
-
•
 $P_S(\lambda )$
is indecomposable.
$P_S(\lambda )$
is indecomposable. -
•
 $(P_S(\lambda ):Z_S(\lambda )) = 1$
.
$(P_S(\lambda ):Z_S(\lambda )) = 1$
. -
•
 $(P_S(\lambda ):Z_S(\mu )) = 0$
unless
$(P_S(\lambda ):Z_S(\mu )) = 0$
unless
 $\mu - \lambda \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
.
$\mu - \lambda \in {\mathbb {Z}}_{\ge 0}\Delta ^+$
.
The module
![]() $\mathcal {V}^{-1}(\mathcal {F}(Q(wA_0)))$
satisfies these conditions with
$\mathcal {V}^{-1}(\mathcal {F}(Q(wA_0)))$
satisfies these conditions with
![]() $\lambda = w\cdot _p\lambda _0$
by the above lemma. We get the following.
$\lambda = w\cdot _p\lambda _0$
by the above lemma. We get the following.
Proposition 3.35. Let
![]() $w\in W^{\prime }_{{\mathrm {aff}}}$
. Then
$w\in W^{\prime }_{{\mathrm {aff}}}$
. Then
![]() $\mathcal {V}(P_S(w\cdot _p\lambda _0)) \simeq \mathcal {F}(Q(wA_0))$
.
$\mathcal {V}(P_S(w\cdot _p\lambda _0)) \simeq \mathcal {F}(Q(wA_0))$
.
The following corollary is obvious from the above proposition.
Corollary 3.36. We have
![]() $[P_{{\mathbb {K}}}(w\cdot _p\lambda _0):Z_{{\mathbb {K}}}(v\cdot _p\lambda _0)] = \operatorname {\mathrm {rank}}(Q(wA_0)_{\{vA_0\}})$
.
$[P_{{\mathbb {K}}}(w\cdot _p\lambda _0):Z_{{\mathbb {K}}}(v\cdot _p\lambda _0)] = \operatorname {\mathrm {rank}}(Q(wA_0)_{\{vA_0\}})$
.
3.9 Lusztig’s conjecture
For
![]() $B\in {\mathcal {S}\mathrm {Bimod}}$
and
$B\in {\mathcal {S}\mathrm {Bimod}}$
and
![]() $w\in W_{{\mathrm {aff}}}$
, let
$w\in W_{{\mathrm {aff}}}$
, let
![]() $B^w$
be the image of
$B^w$
be the image of
![]() $B\hookrightarrow B\otimes _R R^{\emptyset } = \bigoplus _{x\in W_{{\mathrm {aff}}}}B_x^{\emptyset }\twoheadrightarrow B_w^{\emptyset }$
. Put
$B\hookrightarrow B\otimes _R R^{\emptyset } = \bigoplus _{x\in W_{{\mathrm {aff}}}}B_x^{\emptyset }\twoheadrightarrow B_w^{\emptyset }$
. Put
![]() $\operatorname {\mathrm {ch}}(B) = \sum _{w\in W_{{\mathrm {aff}}}}v^{-\ell (w)}\operatorname {\mathrm {grk}}(B^w)$
. Then,
$\operatorname {\mathrm {ch}}(B) = \sum _{w\in W_{{\mathrm {aff}}}}v^{-\ell (w)}\operatorname {\mathrm {grk}}(B^w)$
. Then,
![]() $[B]\mapsto \operatorname {\mathrm {ch}}(B)$
induces an isomorphism
$[B]\mapsto \operatorname {\mathrm {ch}}(B)$
induces an isomorphism
![]() $[{\mathcal {S}\mathrm {Bimod}}]\simeq \mathcal {H}$
. For each
$[{\mathcal {S}\mathrm {Bimod}}]\simeq \mathcal {H}$
. For each
![]() $w\in W_{{\mathrm {aff}}}$
, there exists an indecomposable object
$w\in W_{{\mathrm {aff}}}$
, there exists an indecomposable object
![]() $B(w)\in {\mathcal {S}\mathrm {Bimod}}$
unique up to isomorphism such that
$B(w)\in {\mathcal {S}\mathrm {Bimod}}$
unique up to isomorphism such that
![]() $\operatorname {\mathrm {ch}}(B(w)) \in H_w + \sum _{x < w}{\mathbb {Z}}[v,v^{-1}]H_x$
. We say that
$\operatorname {\mathrm {ch}}(B(w)) \in H_w + \sum _{x < w}{\mathbb {Z}}[v,v^{-1}]H_x$
. We say that
![]() $B(w)$
satisfies the Soergel conjecture if
$B(w)$
satisfies the Soergel conjecture if
![]() $\operatorname {\mathrm {ch}}(B(w))$
is a Kazhdan-Lusztig basis; namely,
$\operatorname {\mathrm {ch}}(B(w))$
is a Kazhdan-Lusztig basis; namely,
![]() $\operatorname {\mathrm {ch}}(B(w))\in H_w + \sum _{x < w}v{\mathbb {Z}}[v]H_x$
. It is known that the Soergel conjecture is satisfied by any
$\operatorname {\mathrm {ch}}(B(w))\in H_w + \sum _{x < w}v{\mathbb {Z}}[v]H_x$
. It is known that the Soergel conjecture is satisfied by any
![]() $B(w)$
over a characteristic zero field. Therefore, for a fixed w, if p is sufficiently large,
$B(w)$
over a characteristic zero field. Therefore, for a fixed w, if p is sufficiently large,
![]() $B(w)$
satisfies the Soergel conjecture (cf. [Reference Elias and WilliamsonEW14]). We fix
$B(w)$
satisfies the Soergel conjecture (cf. [Reference Elias and WilliamsonEW14]). We fix
![]() $\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
and
$\lambda \in ({\mathbb {R}}\Delta )_{{\mathrm {int}}}$
and
![]() $w\in W_{{\mathrm {aff}}}$
such that
$w\in W_{{\mathrm {aff}}}$
such that
![]() $A_{\lambda }^+w\in \Pi _{\lambda }$
. Here,
$A_{\lambda }^+w\in \Pi _{\lambda }$
. Here,
![]() $A_{\lambda }^+$
is the maximal element in
$A_{\lambda }^+$
is the maximal element in
![]() $W^{\prime }_{\lambda }A_{\lambda }^-$
.
$W^{\prime }_{\lambda }A_{\lambda }^-$
.
Lemma 3.37. Let
![]() $w_{\lambda }\in W_{{\mathrm {aff}}}$
such that
$w_{\lambda }\in W_{{\mathrm {aff}}}$
such that
![]() $A_{\lambda }^+w_{\lambda } = A_{\lambda }^-$
. Then, we have
$A_{\lambda }^+w_{\lambda } = A_{\lambda }^-$
. Then, we have
![]() $S_{A_{\lambda }^+}*B(w_{\lambda })\simeq Q_{\lambda }(\ell (w_0))$
.
$S_{A_{\lambda }^+}*B(w_{\lambda })\simeq Q_{\lambda }(\ell (w_0))$
.
Proof. By the translation as in the proof of Lemma 2.31, we may assume
![]() $\lambda = 0$
. Then,
$\lambda = 0$
. Then,
![]() $W_{\lambda }' = W_{\mathrm {f}}$
and it is generated by
$W_{\lambda }' = W_{\mathrm {f}}$
and it is generated by
![]() $S_{{\mathrm {aff}}}\cap W_{\mathrm {f}}$
. Moreover, the element
$S_{{\mathrm {aff}}}\cap W_{\mathrm {f}}$
. Moreover, the element
![]() $w_{\lambda }$
is equal to the longest element
$w_{\lambda }$
is equal to the longest element
![]() $w_0$
.
$w_0$
.
It is sufficient to prove:
![]() $B(w_{0}) \simeq \{(z_w)\in R^{W_{\mathrm {f}}}\mid z_{wt}\equiv z_w\pmod {\alpha _t}\}(\ell (w_0))$
, where t runs through the set of reflections in
$B(w_{0}) \simeq \{(z_w)\in R^{W_{\mathrm {f}}}\mid z_{wt}\equiv z_w\pmod {\alpha _t}\}(\ell (w_0))$
, where t runs through the set of reflections in
![]() $W_{\mathrm {f}}$
and
$W_{\mathrm {f}}$
and
![]() $\alpha _t$
the corresponding element in
$\alpha _t$
the corresponding element in
![]() $\Lambda _{{\mathbb {K}}}$
[Reference AbeAbe21, 2.1]. Let
$\Lambda _{{\mathbb {K}}}$
[Reference AbeAbe21, 2.1]. Let
![]() $(G_{\mathbb {C}}^\vee ,B_{\mathbb {C}}^\vee ,T_{\mathbb {C}}^\vee )$
be the reductive group over
$(G_{\mathbb {C}}^\vee ,B_{\mathbb {C}}^\vee ,T_{\mathbb {C}}^\vee )$
be the reductive group over
![]() $\mathbb {C}$
, the Borel subgroup and the maximal torus with the root datum
$\mathbb {C}$
, the Borel subgroup and the maximal torus with the root datum
![]() $(X^\vee ,\Delta ^\vee ,X,\Delta )$
and the positive system
$(X^\vee ,\Delta ^\vee ,X,\Delta )$
and the positive system
![]() $\Delta ^+\subset \Delta $
. Then, the category of
$\Delta ^+\subset \Delta $
. Then, the category of
![]() ${\mathbb {K}}$
-coefficient parity
${\mathbb {K}}$
-coefficient parity
![]() $B^\vee _{\mathbb {C}}$
-equivariant sheaves on
$B^\vee _{\mathbb {C}}$
-equivariant sheaves on
![]() $G^\vee _{\mathbb {C}}/B_{\mathbb {C}}^\vee $
is equivalent to the category of Soergel bimodules attached to
$G^\vee _{\mathbb {C}}/B_{\mathbb {C}}^\vee $
is equivalent to the category of Soergel bimodules attached to
![]() $(W_{\mathrm {f}},X^\vee _{{\mathbb {K}}})$
[Reference Riche and WilliamsonRW18]. The object
$(W_{\mathrm {f}},X^\vee _{{\mathbb {K}}})$
[Reference Riche and WilliamsonRW18]. The object
![]() $B(w_0)$
corresponds to the indecomposable parity sheaf such that the restriction to the big cell
$B(w_0)$
corresponds to the indecomposable parity sheaf such that the restriction to the big cell
![]() $B_{\mathbb {C}}^\vee w_0B_{\mathbb {C}}^\vee /B_{\mathbb {C}}^\vee $
is
$B_{\mathbb {C}}^\vee w_0B_{\mathbb {C}}^\vee /B_{\mathbb {C}}^\vee $
is
![]() ${\mathbb {K}}_{B_{\mathbb {C}}^\vee w_0B_{\mathbb {C}}^\vee /B_{\mathbb {C}}^\vee }[\ell (w_0)]$
. It is obvious that the constant sheaf
${\mathbb {K}}_{B_{\mathbb {C}}^\vee w_0B_{\mathbb {C}}^\vee /B_{\mathbb {C}}^\vee }[\ell (w_0)]$
. It is obvious that the constant sheaf
![]() ${\mathbb {K}}_{G^\vee _{\mathbb {C}}/B_{\mathbb {C}}^\vee }[\ell (w_0)]$
satisfies this condition, and therefore, the constant sheaf corresponds to
${\mathbb {K}}_{G^\vee _{\mathbb {C}}/B_{\mathbb {C}}^\vee }[\ell (w_0)]$
satisfies this condition, and therefore, the constant sheaf corresponds to
![]() $B(w_0)$
. By the main theorem of [Reference Fiebig and WilliamsonFW14], the corresponding Soergel bimodule is given as above.
$B(w_0)$
. By the main theorem of [Reference Fiebig and WilliamsonFW14], the corresponding Soergel bimodule is given as above.
Recall that we took
![]() $w\in W_{{\mathrm {aff}}}$
and
$w\in W_{{\mathrm {aff}}}$
and
![]() $\lambda \in ({\mathbb {R}}\Phi _{{\mathrm {int}}})$
such that
$\lambda \in ({\mathbb {R}}\Phi _{{\mathrm {int}}})$
such that
![]() $A_{\lambda }^+w\in \Pi _{\lambda }$
. Define
$A_{\lambda }^+w\in \Pi _{\lambda }$
. Define
![]() $S_{A_{\lambda }^{+}}\in \widetilde {\mathcal {K}}'(S)$
as follows:
$S_{A_{\lambda }^{+}}\in \widetilde {\mathcal {K}}'(S)$
as follows:
![]() $S_{A_{\lambda }^{+}} = S$
as a left S-module and R acts through
$S_{A_{\lambda }^{+}} = S$
as a left S-module and R acts through
![]() $f\mapsto f_{A}$
. We have
$f\mapsto f_{A}$
. We have
![]() $(S_{A_{\lambda }^{+}})_{A_{\lambda }^{+}}^{\emptyset } = S^{\emptyset }$
and
$(S_{A_{\lambda }^{+}})_{A_{\lambda }^{+}}^{\emptyset } = S^{\emptyset }$
and
![]() $(S_{A_{\lambda }^{+}})_{A'}^{\emptyset } = 0$
for
$(S_{A_{\lambda }^{+}})_{A'}^{\emptyset } = 0$
for
![]() $A'\in \mathcal {A}\setminus \{A_{\lambda }^{+}\}$
.
$A'\in \mathcal {A}\setminus \{A_{\lambda }^{+}\}$
.
Theorem 3.38. If
![]() $B(w)$
satisfies the Soergel conjecture, then
$B(w)$
satisfies the Soergel conjecture, then
![]() $S_{A_{\lambda }^+}*B(w)\simeq Q(A_{\lambda }^+w)$
.
$S_{A_{\lambda }^+}*B(w)\simeq Q(A_{\lambda }^+w)$
.
Proof. First, we prove that
![]() $S_{A_{\lambda }^+}*B(w)\in \mathcal {K}_P$
. By the translation as in Lemma 2.31, we may assume
$S_{A_{\lambda }^+}*B(w)\in \mathcal {K}_P$
. By the translation as in Lemma 2.31, we may assume
![]() $\lambda = 0$
. Then,
$\lambda = 0$
. Then,
![]() $W_{\lambda }' = W_{\mathrm {f}}$
, and this is isomorphic to the subgroup of
$W_{\lambda }' = W_{\mathrm {f}}$
, and this is isomorphic to the subgroup of
![]() $W_{{\mathrm {aff}}}$
generated by
$W_{{\mathrm {aff}}}$
generated by
![]() $s\in S_{{\mathrm {aff}}}$
which contains a hyperplance through
$s\in S_{{\mathrm {aff}}}$
which contains a hyperplance through
![]() $0$
. We identify
$0$
. We identify
![]() $W_{\mathrm {f}}\hookrightarrow W_{{\mathrm {aff}}}$
. We have
$W_{\mathrm {f}}\hookrightarrow W_{{\mathrm {aff}}}$
. We have
![]() $sw < w$
for any
$sw < w$
for any
![]() $s\in W_{\mathrm {f}}\cap S_{{\mathrm {aff}}}$
. Therefore,
$s\in W_{\mathrm {f}}\cap S_{{\mathrm {aff}}}$
. Therefore,
![]() $H_s\operatorname {\mathrm {ch}}(B(w)) = v^{-1}\operatorname {\mathrm {ch}}(B(w))$
by [Reference Jensen and WilliamsonJW17, Lemma 4.3]. Hence,
$H_s\operatorname {\mathrm {ch}}(B(w)) = v^{-1}\operatorname {\mathrm {ch}}(B(w))$
by [Reference Jensen and WilliamsonJW17, Lemma 4.3]. Hence,
![]() $H_x\operatorname {\mathrm {ch}}(B(w)) = v^{-\ell (x)}\operatorname {\mathrm {ch}}(B(w))$
for any
$H_x\operatorname {\mathrm {ch}}(B(w)) = v^{-\ell (x)}\operatorname {\mathrm {ch}}(B(w))$
for any
![]() $x\in W_{\mathrm {f}}$
. Take
$x\in W_{\mathrm {f}}$
. Take
![]() $a_{y} = \sum _{n\in {\mathbb {Z}}}a_{y,n}v^{n}\in {\mathbb {Z}}_{\ge 0}[v,v^{-1}]$
such that
$a_{y} = \sum _{n\in {\mathbb {Z}}}a_{y,n}v^{n}\in {\mathbb {Z}}_{\ge 0}[v,v^{-1}]$
such that
![]() $\operatorname {\mathrm {ch}}(B(w_{0})) = \sum _{y\in W_{\mathrm {f}}}a_{y}H_{y}$
(one can write
$\operatorname {\mathrm {ch}}(B(w_{0})) = \sum _{y\in W_{\mathrm {f}}}a_{y}H_{y}$
(one can write
![]() $a_{y}$
explicitly, but we do not do this here because we will not use this). Then, we have
$a_{y}$
explicitly, but we do not do this here because we will not use this). Then, we have
![]() $\operatorname {\mathrm {ch}}(B(w_{0})\otimes B(w)) = \sum _{y\in W_{\mathrm {f}}}a_{y}v^{- \ell (y)}\operatorname {\mathrm {ch}}(B(w))$
. Hence, we get
$\operatorname {\mathrm {ch}}(B(w_{0})\otimes B(w)) = \sum _{y\in W_{\mathrm {f}}}a_{y}v^{- \ell (y)}\operatorname {\mathrm {ch}}(B(w))$
. Hence, we get
![]() $B(w_{0})\otimes B(w)\simeq \bigoplus _{y\in W_{\mathrm {f}},n\in {\mathbb {Z}}}B(w)^{a_{y,n}}(n - \ell (y))$
. Therefore, up to shift,
$B(w_{0})\otimes B(w)\simeq \bigoplus _{y\in W_{\mathrm {f}},n\in {\mathbb {Z}}}B(w)^{a_{y,n}}(n - \ell (y))$
. Therefore, up to shift,
![]() $S_{A_{0}^+}*B(w)$
is a direct summand of
$S_{A_{0}^+}*B(w)$
is a direct summand of
![]() $S_{A_{0}^+}*(B(w_{0})\otimes B(w))\simeq Q_{0}(\ell (w_{0}))*B(w)\in \mathcal {K}_P$
. Hence,
$S_{A_{0}^+}*(B(w_{0})\otimes B(w))\simeq Q_{0}(\ell (w_{0}))*B(w)\in \mathcal {K}_P$
. Hence,
![]() $S_{A_{0}^+}*B(w)\in \mathcal {K}_P$
.
$S_{A_{0}^+}*B(w)\in \mathcal {K}_P$
.
We return to the proof of the theorem. By [Reference LusztigLus80, Theorem 5.2],
![]() $\operatorname {\mathrm {ch}}(S_{A_{\lambda }^+}*B(w)) = A_{\lambda }^+\operatorname {\mathrm {ch}}(B(w))$
is described by periodic Kazhdan-Lusztig polynomials; namely, we have
$\operatorname {\mathrm {ch}}(S_{A_{\lambda }^+}*B(w)) = A_{\lambda }^+\operatorname {\mathrm {ch}}(B(w))$
is described by periodic Kazhdan-Lusztig polynomials; namely, we have
![]() $A_{\lambda }^+\operatorname {\mathrm {ch}}(B(w)) = v^{-n}\underline {P}_{A_0}$
for some
$A_{\lambda }^+\operatorname {\mathrm {ch}}(B(w)) = v^{-n}\underline {P}_{A_0}$
for some
![]() $A_0\in \mathcal {A}$
and
$A_0\in \mathcal {A}$
and
![]() $n\in {\mathbb {Z}}$
. Here,
$n\in {\mathbb {Z}}$
. Here,
![]() $\underline {P}_{A'}\in \mathcal {P}^0$
is the element given in [Reference SoergelSoe97, Proposition 4.16]. We know
$\underline {P}_{A'}\in \mathcal {P}^0$
is the element given in [Reference SoergelSoe97, Proposition 4.16]. We know
![]() $A_{\lambda }^+\operatorname {\mathrm {ch}}(B(w))\in A_{\lambda }^+w + \sum _{A'> A_{\lambda }^+w}{\mathbb {Z}}[v,v^{-1}]A'$
. Comparing with [Reference SoergelSoe97, Lemma 4.21], we have
$A_{\lambda }^+\operatorname {\mathrm {ch}}(B(w))\in A_{\lambda }^+w + \sum _{A'> A_{\lambda }^+w}{\mathbb {Z}}[v,v^{-1}]A'$
. Comparing with [Reference SoergelSoe97, Lemma 4.21], we have
![]() $n = \ell (w_0)$
and
$n = \ell (w_0)$
and
![]() $\operatorname {\mathrm {ch}}(S_{A_{\lambda }^+}*B(w))\in A_{\lambda }^+w + \sum _{A'> A_{\lambda }^+w}v^{- 1}{\mathbb {Z}}[v^{-1}]A'$
. By the self-duality of
$\operatorname {\mathrm {ch}}(S_{A_{\lambda }^+}*B(w))\in A_{\lambda }^+w + \sum _{A'> A_{\lambda }^+w}v^{- 1}{\mathbb {Z}}[v^{-1}]A'$
. By the self-duality of
![]() $\underline {P}_{A_0}$
, we have
$\underline {P}_{A_0}$
, we have
![]() $\overline {\operatorname {\mathrm {ch}}(S_{A_{\lambda }^+}*B(w))} = v^{\ell (w_0)}\underline {P}_{A_0}\in v^{2\ell (w_0)}A_{\lambda }^+w + \sum _{A'> A_{\lambda }^+w}v^{2\ell (w_0)- 1}{\mathbb {Z}}[v^{-1}]A'$
. Therefore, by Theorem 3.10, we have
$\overline {\operatorname {\mathrm {ch}}(S_{A_{\lambda }^+}*B(w))} = v^{\ell (w_0)}\underline {P}_{A_0}\in v^{2\ell (w_0)}A_{\lambda }^+w + \sum _{A'> A_{\lambda }^+w}v^{2\ell (w_0)- 1}{\mathbb {Z}}[v^{-1}]A'$
. Therefore, by Theorem 3.10, we have
Hence,
![]() $\operatorname {\mathrm {End}}_{\mathcal {K}}(S_{A_{\lambda }^+}*B(w))$
is one-dimensional, and therefore,
$\operatorname {\mathrm {End}}_{\mathcal {K}}(S_{A_{\lambda }^+}*B(w))$
is one-dimensional, and therefore,
![]() $1$
and
$1$
and
![]() $0$
are only its idempotents. Therefore,
$0$
are only its idempotents. Therefore,
![]() $S_{A_{\lambda }^+}*B(w)$
is indecomposable. Since
$S_{A_{\lambda }^+}*B(w)$
is indecomposable. Since
![]() $Q({A_{\lambda }^+w})$
is a direct summand of
$Q({A_{\lambda }^+w})$
is a direct summand of
![]() $S_{A_{\lambda }^+}*B(w)$
, we get the theorem.
$S_{A_{\lambda }^+}*B(w)$
, we get the theorem.
From the above theorem and Corollary 3.36, the multiplicity of the baby Verma modules in the projective cover of an irreducible module is given by the value at
![]() $1$
of the Kazhdan-Lusztig polynomial. Hence, the Lusztig’s conjecture holds for sufficiently large p.
$1$
of the Kazhdan-Lusztig polynomial. Hence, the Lusztig’s conjecture holds for sufficiently large p.
Acknowledgements
The question treated in this paper was asked by Masaharu Kaneda. The author had many helpful discussions with him. He also thank the referees giving helpful comments and pointing out errors. The author was supported by JSPS KAKENHI Grant Number 18H01107.
Competing Interest
None.