Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T01:15:34.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Global well-posedness for 3D Navier–Stokes equations with ill-prepared initial data

Published online by Cambridge University Press:  19 July 2013

Marius Paicu  and
Zhifei Zhang
Marius Paicu
Affiliation:
Université Bordeaux 1 Institut de Mathématiques de Bordeaux F-33405 Talence Cedex, France ([email protected])
Zhifei Zhang
Affiliation:
LMAM and School of Mathematical Sciences, Peking University, 100871, PR China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

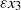We study the global well-posedness of 3D Navier–Stokes equations for a class of large initial data. This type of data slowly varies in the vertical direction (expressed as a function of $\varepsilon {x}_{3} $), and it is ill-prepared in the sense that its norm in 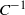${C}^{- 1} $ will blow up at the rate 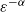${\varepsilon }^{- \alpha } $ for 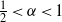$\frac{1}{2} \lt \alpha \lt 1$ as $\varepsilon $ tends to zero.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 2 , April 2014 , pp. 395 - 411
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alinhac, S. and Métivier, G., Propagation de l’analyticité locale pour les solutions de l’équation d’Euler, Arch. Ration. Mech. Anal. 92 (4) (1986), 287–296.CrossRefGoogle Scholar
Bahouri, H. and Gallagher, I., Weak stability of the set of global solutions to the Navier–Stokes equations, Arch. Ration. Mech. Anal. 209 (2) (2013), 569–629.Google Scholar
Bardos, C., Analyticité de la solution de l’équation d’Euler dans un ouvert de ${R}^{n} $ , C. R. Acad. Sci. Paris Sér. A–B 283 (5)(1976), Aii, A255–A258.Google Scholar
Bardos, C. and Benachour, S., Domaine d’analycité des solutions de l’équation d’Euler dans un ouvert de ${R}^{n} $ , Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 4 (1977), 647–687.Google Scholar
Bony, J.-M., Calcul symbolique et propagation des singularités pour les équations aux dérivées partielles non linéaires, Ann. Sci. Éc. Norm. Supér. 14 (1981), 209–246.CrossRefGoogle Scholar
Chemin, J.-Y., Le système de Navier–Stokes incompressible soixante dix ans après Jean Leray, Sémin. Congr. 9 (2004), 99–123.Google Scholar
Chemin, J.-Y., Desjardins, B., Gallagher, I. and Grenier, E., Fluids with anisotropic viscosity, Modél. Math. Anal. Numér. 34 (2000), 315–335.Google Scholar
Chemin, J.-Y. and Gallagher, I., On the global wellposedness of the 3-D Navier–Stokes equations with large initial data, Ann. Sci. Éc. Norm. Supér. 39 (2006), 679–698.Google Scholar
Chemin, J.-Y. and Gallagher, I., Wellposedness and stability results for the Navier–Stokes equations in  ${\mathbf{R} }^{3} $ , Ann. Inst. H. Poincaré Anal. Non Linéaire 26 (2009), 599–624.Google Scholar
Chemin, J.-Y. and Gallagher, I., Large, global solutions to the Navier–Stokes equations, slowly varying in one direction, Trans. Amer. Math. Soc. 362 (2010), 2859–2873.Google Scholar
Chemin, J.-Y., Gallagher, I. and Mullaert, C., The role of spectral anisotropy in the resolution of the three-dimensional Navier–Stokes equations (arXiv:1205.6992).Google Scholar
Chemin, J.-Y., Gallagher, I. and Paicu, M., Global regularity for some classes of large solutions to the Navier–Stokes equations, Ann. of Math. 173 (2011), 983–1012.Google Scholar
Chemin, J.-Y., Gallagher, I. and Zhang, P., Sums of large global solutions to the incompressible Navier–Stokes equations, J. Reine Angew. Math., in press.Google Scholar
Foias, C. and Temam, R., Gevrey class regularity for the solutions of the Navier–Stokes equations, J. Funct. Anal. 87 (1989), 359–369.CrossRefGoogle Scholar
Levermore, C. D. and Oliver, M., Analyticity of solutions for a generalized Euler equation, J. Differential Equations 133 (2) (1997), 321–339.CrossRefGoogle Scholar
Paicu, M., Équation anisotrope de Navier–Stokes dans des espaces critiques, Revista Rev. Matemtica Iberoam. 21 (2005), 179–235.CrossRefGoogle Scholar
Paicu, M. and Zhang, Z., Global regularity for the Navier–Stokes equations with some classes of large initial data, Anal. PDE 4 (2011), 95–113.CrossRefGoogle Scholar
Sammartino, M. and Caflisch, R. E., Zero viscosity limit for analytic solutions, of the Navier–Stokes equation on a half-space. I. Existence for Euler and Prandtl equations, Comm. Math. Phys. 192 (1998), 433–461.CrossRefGoogle Scholar