No CrossRef data available.
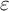 $\varepsilon $-FACTORS IN HIGHER DIMENSIONS
$\varepsilon $-FACTORS IN HIGHER DIMENSIONSPublished online by Cambridge University Press: 02 September 2021
We prove a product formula for the determinant of the cohomology of an étale sheaf with 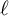 $\ell $
-adic coefficients over an arbitrary proper scheme over a perfect field of positive characteristic p distinct from
$\ell $
-adic coefficients over an arbitrary proper scheme over a perfect field of positive characteristic p distinct from 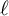 $\ell $
. The local contributions are constructed by iterating vanishing cycle functors as well as certain exact additive functors that can be considered as linearised versions of Artin conductors and local
$\ell $
. The local contributions are constructed by iterating vanishing cycle functors as well as certain exact additive functors that can be considered as linearised versions of Artin conductors and local 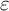 $\varepsilon $
-factors. We provide several applications of our higher dimensional product formula, such as twist formulas for global
$\varepsilon $
-factors. We provide several applications of our higher dimensional product formula, such as twist formulas for global 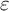 $\varepsilon $
-factors.
$\varepsilon $
-factors.