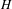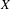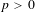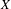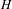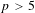Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ma, Linquan
Schwede, Karl
Tucker, Kevin
Waldron, Joe
and
Witaszek, Jakub
2022.
An analogue of adjoint ideals and PLT singularities in mixed characteristic.
Journal of Algebraic Geometry,
Vol. 31,
Issue. 3,
p.
497.
Das, Omprokash
and
Waldron, Joe
2022.
On the log minimal model program for threefolds over imperfect fields of characteristic p>5$p>5$.
Journal of the London Mathematical Society,
Vol. 106,
Issue. 4,
p.
3895.
Tanaka, Hiromu
2024.
Bertini theorems admitting base changes.
Journal of Algebra,
Vol. 644,
Issue. ,
p.
64.
Takahashi, Ryo
2025.
Proxy small thick subcategories of derived categories.
Journal of Algebra,
Vol. 662,
Issue. ,
p.
465.