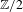Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-10T06:36:43.882Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVARIANT CALCULUS OF FUNCTORS AND$\mathbb{Z}/2$-ANALYTICITY OF REAL ALGEBRAIC 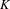$K$-THEORY

Part of: Homotopy theory $K$-theory of forms

Published online by Cambridge University Press:  01 April 2015

Emanuele Dotto
Emanuele Dotto*
Affiliation:
Mathematics, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Building E18, Cambridge, 02139-4307, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We define a theory of Goodwillie calculus for enriched functors from finite pointed simplicial 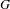$G$-sets to symmetric 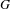$G$-spectra, where 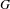$G$ is a finite group. We extend a notion of 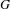$G$-linearity suggested by Blumberg to define stably excisive and 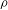${\it\rho}$-analytic homotopy functors, as well as a 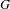$G$-differential, in this equivariant context. A main result of the paper is that analytic functors with trivial derivatives send highly connected 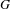$G$-maps to 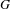$G$-equivalences. It is analogous to the classical result of Goodwillie that ‘functors with zero derivative are locally constant’. As the main example, we show that Hesselholt and Madsen’s Real algebraic 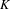$K$-theory of a split square zero extension of Wall antistructures defines an analytic functor in the 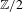$\mathbb{Z}/2$-equivariant setting. We further show that the equivariant derivative of this Real 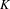$K$-theory functor is 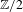$\mathbb{Z}/2$-equivalent to Real MacLane homology.

Keywords

Hermitian K-theoryequivariant homotopy theory

MSC classification

Primary: 19G38: Hermitian $K$-theory, relations with $K$-theory of rings 55P91: Equivariant homotopy theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 4 , October 2016 , pp. 829 - 883
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arone, G., A generalization of Snaith-type filtration, Trans. Amer. Math. Soc. 351(3) (1999), 1123–1150; MR 1638238 (99i:55011).CrossRefGoogle Scholar
Biedermann, G., Chorny, B. and Röndigs, O., Calculus of functors and model categories, Adv. Math. 214(1) (2007), 92–115; MR 2348024 (2008k:55036).Google Scholar
Biedermann, G. and Röndigs, O., Calculus of functors and model categories, II, Algebr. Geom. Topol. 14(5) (2014), 2853–2913; MR 3276850.Google Scholar
Blumberg, A. J., Continuous functors as a model for the equivariant stable homotopy category, Algebr. Geom. Topol. 6 (2006), 2257–2295; MR 2286026 (2008a:55006).CrossRefGoogle Scholar
Dundas, B. I., Goodwillie, T. G. and McCarthy, R., The Local Structure of Algebraic K-Theory, Algebra and Applications, Volume 18 (Springer-Verlag London Ltd., London, 2013); MR 3013261.Google Scholar
Dundas, B. I. and McCarthy, R., Stable K-theory and topological Hochschild homology, Ann. of Math. (2) 140(3) (1994), 685–701; MR 1307900 (96e:19005a).Google Scholar
Dotto, E., Stable real algebraic $K$ -theory and real topological Hochschild homology, PhD thesis, University of Copenhagen (2012) arXiv:1212.4310.Google Scholar
Fiedorowicz, Z., Pirashvili, T., Schwänzl, R., Vogt, R. and Waldhausen, F., Mac Lane homology and topological Hochschild homology, Math. Ann. 303(1) (1995), 149–164; MR 1348360 (97h:19007).Google Scholar
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory, Progress in Mathematics, Volume 174 (Birkhäuser Verlag, Basel, 1999); MR 1711612 (2001d:55012).Google Scholar
Goodwillie, T. G., Calculus. I. The first derivative of pseudoisotopy theory, K-Theory 4(1) (1990), 1–27; MR 1076523 (92m:57027).Google Scholar
Goodwillie, T. G., Calculus. III. Taylor series, Geom. Topol. 7 (2003), 645–711; (electronic) MR 2026544 (2005e:55015).Google Scholar
Goodwillie, T. G., Calculus. II. Analytic functors, K-Theory 5(4) (1991/92), 295–332; MR 1162445 (93i:55015).CrossRefGoogle Scholar
Hesselholt, L. and I. Madsen, Real algebraic $K$ -theory (2015) (to appear).Google Scholar
Hirschhorn, P. S., Model Categories and Their Localizations, Mathematical Surveys and Monographs, Volume 99 (American Mathematical Society, Providence, RI, 2003); MR 1944041 (2003j:18018).Google Scholar
Hornbostel, J., Constructions and dévissage in Hermitian K-theory, K-Theory 26(2) (2002), 139–170; MR 1931219 (2003i:19002).CrossRefGoogle Scholar
Lurie, J., Higher algebra (2015); http://www.math.harvard.edu/∼lurie/papers/higheralgebra.pdf.Google Scholar
Mandell, M. A., Equivariant symmetric spectra, in Homotopy Theory: Relations with Algebraic Geometry, Group Cohomology, and Algebraic K-Theory, Contemporary Mathematics, Volume 346, pp. 399–452 (American Mathematical Society, Providence, RI, 2004); MR 2066508 (2005d:55019).Google Scholar
Mandell, M. A. and May, J. P., Equivariant orthogonal spectra and S-modules, Mem. Amer. Math. Soc. 159(755) (2002), x+108; MR 1922205 (2003i:55012).Google Scholar
McCarthy, R., Relative algebraic K-theory and topological cyclic homology, Acta Math. 179(2) (1997), 197–222; MR 1607555 (99e:19006).CrossRefGoogle Scholar
Schlichting, M., Hermitian K-theory of exact categories, J. K-Theory 5(1) (2010), 105–165; MR 2600285 (2011b:19007).Google Scholar
Schwede, S., Lectures on equivariant stable homotopy theory (2015); http://www.math.uni-bonn.de/∼schwede/equivariant.pdf.Google Scholar
Segal, G., Configuration-spaces and iterated loop-spaces, Invent. Math. 21 (1973), 213–221; MR 0331377 (48 #9710).Google Scholar
Shimakawa, K., Infinite loop G-spaces associated to monoidal G-graded categories, Publ. Res. Inst. Math. Sci. 25(2) (1989), 239–262; MR 1003787 (90k:55017).Google Scholar
Shipley, B., A convenient model category for commutative ring spectra, in Homotopy Theory: Relations with Algebraic Geometry, Group Cohomology, and Algebraic K-theory, Contemporary Mathematics, Volume 346, pp. 473–483 (American Mathematical Society, Providence, RI, 2004); MR 2066511 (2005d:55014).Google Scholar
Vogell, W., The involution in the algebraic K-theory of spaces, in Algebraic and Geometric Topology (New Brunswick, NJ, 1983), Lecture Notes in Mathematics, Volume 1126, pp. 277–317 (Springer, Berlin, 1985); MR 802795 (87e:55009).Google Scholar
Waldhausen, F., Algebraic K-theory of spaces, in Algebraic and Geometric Topology (New Brunswick, NJ, 1983), Lecture Notes in Mathematics, Volume 1126, pp. 318–419 (Springer, Berlin, 1985); MR 802796 (86m:18011).CrossRefGoogle Scholar
Wall, C. T. C., On the axiomatic foundations of the theory of Hermitian forms, Proc. Cambridge Philos. Soc. 67 (1970), 243–250; MR 0251054 (40 #4285).Google Scholar
Weiss, M. and Williams, B., Duality in Waldhausen categories, Forum Math. 10(5) (1998), 533–603; MR 1644309 (99g:19002).Google Scholar