Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-22T06:09:32.640Z Has data issue: false hasContentIssue false
  • English
  • Français

EPSTEIN ZETA-FUNCTIONS, SUBCONVEXITY, AND THE PURITY CONJECTURE

Part of: Partial differential equations on manifolds; differential operators Zeta and $L$-functions: analytic theory Forms and linear algebraic groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  02 April 2018

Valentin Blomer
Valentin Blomer*
Affiliation:
Mathematisches Institut, Bunsenstr. 3-5, 37073 Göttingen, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Subconvexity bounds on the critical line are proved for general Epstein zeta-functions of 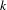$k$-ary quadratic forms. This is related to sup-norm bounds for unitary Eisenstein series on 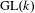$\text{GL}(k)$ associated with the maximal parabolic of type 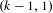$(k-1,1)$, and the exact sup-norm exponent is determined to be 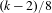$(k-2)/8$ for 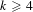$k\geqslant 4$. In particular, if 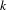$k$ is odd, this exponent is not in 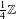$\frac{1}{4}\mathbb{Z}$, which is relevant in the context of Sarnak’s purity conjecture and shows that it can in general not directly be generalized to Eisenstein series.

Keywords

Epstein zeta-functionquadratic formssubconvexitysup-normsSarnak’s purity conjecturemultiple Dirichlet series

MSC classification

Primary: 11M36: Selberg zeta functions and regularized determinants; applications to spectral theory, Dirichlet series, Eisenstein series, etc. Explicit formulas 11E45: Analytic theory (Epstein zeta functions; relations with automorphic forms and functions)
Secondary: 11F68: Dirichlet series in several complex variables associated to automorphic forms; Weyl group multiple Dirichlet series 58J50: Spectral problems; spectral geometry; scattering theory
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 581 - 596
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author was supported in part by SNF-DFG grant BL 915/2 and NSF grant 1128155 while enjoying the hospitality of the Institute for Advanced Study. The United States Government is authorized to reproduce and distribute reprints notwithstanding any copyright notation herein.

References

Andersson, J. and Södergren, A., On the universality of the Epstein zeta function, Preprint, 2015, arXiv:1508.05836.Google Scholar
Arthur, J., A trace formula for reductive groups. II. Applications of a truncation operator, Compos. Math. 40 (1980), 87–121.Google Scholar
Balasubramanian, R., Ivić, A. and Ramachandra, K., The mean square of the Riemann zeta-function on the line 𝜎 = 1, Enseign. Math. 38 (1992), 13–25.Google Scholar
Blomer, V., Subconvexity for a double Dirichlet series, Compos. Math. 147 (2011), 355–374.Google Scholar
Blomer, V., Khan, R. and Young, M., Distribution of mass of holomorphic cusp forms, Duke Math. J. 162 (2013), 2609–2644.Google Scholar
Brumley, F. and Templier, N., Large values of cusp forms on $\text{GL}(n)$, Preprint, 2013,arXiv:1411.4317.Google Scholar
Chandrasekharan, K. and Narasimhan, R., The approximate functional equation for a class of zeta-functions, Math. Ann. 152 (1963), 30–64.Google Scholar
Cohen, H., Sums involving the values at negative integers of L-functions of quadratic characters, Math. Ann. 217 (1975), 271–285.Google Scholar
Donnelly, H., Exceptional sequences of eigenfunctions for hyperbolic manifolds, Proc. Amer. Math. Soc. 135 (2007), 1551–1555.Google Scholar
Epstein, P., Zur Theorie allgemeiner Zetafunctionen, Math. Ann. 56 (1903), 615–644.Google Scholar
Fomenko, O. M., The order of the Epstein zeta-function in the critical strip, J. Math. Sci. (N.Y.) 110 (2002), 3150–3163. translation.Google Scholar
Goldfeld, D., Automorphic forms and L-functions for the group GL(n, ℝ), Cambridge Studies in Advanced Mathematics, Volume 99 (Cambridge University Press, 2006).Google Scholar
Good, A., Beiträge zur Theorie der Dirichletreihen, die Spitzenformen zugeordnet sind, J. Number Theory 13 (1981), 18–65.Google Scholar
Götze, F., Lattice point problems and values of quadratic forms, Invent. Math. 157 (2004), 195–226.Google Scholar
Hecke, E., Über Modulfunktionen und Dirichletsche Reihen mit Eulerscher Produktentwicklung II, Math. Ann. 114 (1937), 316–351.Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory, Volume 53 (AMS Colloquium Publications, Providence, 2004).Google Scholar
Iwaniec, H. and Sarnak, P., L ∞ norms of eigenfunctions of arithmetic surfaces, Ann. of Math. 141 (1995), 301–320.Google Scholar
Iwaniec, H. and Sarnak, P., Perspectives on the analytic theory of L-functions, GAFA Special volume, pp. 705–741. (2000).Google Scholar
Jarník, V., Über Gitterpunkte in mehrdimensionalen Ellipsoiden, Math. Ann. 100 (1928), 699–721.Google Scholar
Lapid, E. and Offen, O., Compact unitary periods, Compositio Math. 143 (2007), 323–338.Google Scholar
Milićević, D., Large values of eigenfunctions on arithmetic hyperbolic surfaces, Geom. Funct. Anal. 21 (2011), 1375–1418.Google Scholar
Miller, S. D., On the existence and temperedness of cusp forms for SL3(ℤ), J. Reine Angew. Math. 533 (2001), 127–169.Google Scholar
Rudnick, Z. and Sarnak, P., The behavior of eigenstates of arithmetic hyperbolic manifolds, Comm. Math. Phys. 161 (1994), 195–213.Google Scholar
Sarnak, P., Letter to Morawetz http://www.math.princeton.edu/sarnak.Google Scholar
Shimura, G., The Representation of Integers as Sums of Squares, Amer. J. Math. 124 (2002), 1059–1081.Google Scholar
Siegel, C. L., Über die analytische Theorie der quadratischen Formen, Ann. of Math. 36 (1935), 527–606.Google Scholar
Sono, K., Higher moments of the Epstein zeta functions, Tokyo J. of Math. 36 (2013), 269–287.Google Scholar
Spinu, F., The $L^{4}$ norm of the Eisenstein series, thesis, Princeton (2003).Google Scholar
Titchmarsh, E. C., On Epstein’s zeta-function, Proc. Lond. Math. Soc. (2) 36 (1934), 485–500.Google Scholar
Young, M., A note on the sup norm of Eisenstein series, Quart. J. Math., to appear.Google Scholar
Zhang, L., Quantum unique ergodicity of degenerate Eisenstein series on $\text{GL}(n)$, Preprint, 2016, arXiv:1609:01386.Google Scholar