Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T10:19:46.309Z Has data issue: false hasContentIssue false
  • English
  • Français

ENFORCEABLE OPERATOR ALGEBRAS

Part of: Model theory Selfadjoint operator algebras

Published online by Cambridge University Press:  01 March 2019

Isaac Goldbring
Isaac Goldbring*
Affiliation:
Department of Mathematics, University of California, Irvine, Irvine, CA92697, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We adapt the classical notion of building models by games to the setting of continuous model theory. As an application, we study to what extent canonical operator algebras are enforceable models. For example, we show that the hyperfinite II1 factor is an enforceable II1 factor if and only if the Connes Embedding Problem has a positive solution. We also show that the set of continuous functions on the pseudoarc is an enforceable model of the theory of unital, projectionless, abelian 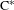$\text{C}^{\ast }$-algebras and use this to show that it is the prime model of its theory.

Keywords

model-theoretic forcinglocally universal objectsoperator algebras

MSC classification

Primary: 03C25: Model-theoretic forcing 03C98: Applications of model theory 03C20: Ultraproducts and related constructions 46L05: General theory of $C^*$-algebras 46L10: General theory of von Neumann algebras
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 1 , January 2021 , pp. 31 - 63
Check for updates
Copyright
© Cambridge University Press 2019

References

Bankston, P., The Chang–Łoś–Suszko theorem in a topological setting, Arch. Math. Logic 45 (2006), 97–112.CrossRefGoogle Scholar
Bellamy, D., Mapping hereditarily indecomposable continua onto a pseudo-arc, in Topology Conference (Virginia Polytech. Inst. and State Univ., Blacksburg, VA, 1973), Volume 375, pp. 6–14 (Springer, Berlin, 1974).CrossRefGoogle Scholar
Ben Yaacov, I., Topometric spaces and perturbations of metric structures, Log. Anal. 1 (2008), 235–272.CrossRefGoogle Scholar
Ben Yaacov, I., Berenstein, A., Henson, C. W. and Usvyatsov, A., Model theory for metric structures, in Model Theory with Applications to Algebra and Analysis, London Mathematical Society Lecture Note Series (350), Volume 2, pp. 315–427 (Cambridge University Press, Cambridge, 2008).CrossRefGoogle Scholar
Ben Yaacov, I. and Iovino, J., Model theoretic forcing in analysis, Ann. Pure Appl. Logic 158 (2009), 163–174.CrossRefGoogle Scholar
Carlson, K., Cheung, E., Gerhardt-Bourke, A., Farah, I., Hart, B., Mezuman, L., Sequeira, N. and Sherman, A., Omitting types and AF algebras, Arch. Math. Logic 53 (2014), 157–169.CrossRefGoogle Scholar
Eagle, C., Goldbring, I. and Vignati, A., The pseudoarc is a co-existentially closed continuum, Topology Appl. 207 (2016), 1–9.CrossRefGoogle Scholar
Farah, I., Absoluteness, truth, and quotients, in Proceedings of the IMS Workshop on Infinity and Truth,(ed. Chong, C.T. ), pp. 1–24 (World Scientific).Google Scholar
Farah, I., Goldbring, I., Hart, B. and Sherman, D., Existentially closed II1-factors, Fund. Math. 233 (2016), 173–196.Google Scholar
Farah, I., Hart, B., Lupini, M., Robert, L., Tikuisis, A.P., Vignati, A. and Winter, W., Model theory of $C^{\ast }$ -algebras, preprint, 2016, arXiv:1602.08072.Google Scholar
Farah, I., Hart, B., Tikuisis, A. and Rordam, M., Relative commutants of strongly self-absorbing C∗ -algebras, Selecta Math. 23 (2017), 363–387.CrossRefGoogle Scholar
Farah, I., Hart, B. and Sherman, D., Model theory of operator algebras II: Model theory, Israel J. Math. 201 (2014), 477–505.CrossRefGoogle Scholar
Farah, I., Hart, B. and Sherman, D., Model theory of operator algebras III: Elementary equivalence and II1 factors, Bull. Lond. Math. Soc. 46 (2014), 1–20.CrossRefGoogle Scholar
Farah, I. and Magidor, M., Omitting types in the logic of metric structures, J. Math. Logic 18(2) (2018), 1–58.CrossRefGoogle Scholar
Goldbring, I., Hart, B. and Sinclair, T., The theory of tracial von Neumann algebras does not have a model companion, J. Symbolic Log. 78 (2013), 1000–1004.CrossRefGoogle Scholar
Goldbring, I. and Lupini, M., Model theoretic properties of the Gurarij operator system, Israel J. Math. 226 (2018), 87–118.CrossRefGoogle Scholar
Goldbring, I. and Sinclair, T., On Kirchberg’s Embedding Problem, J. Funct. Anal. 269 (2015), 155–198.CrossRefGoogle Scholar
Goldbring, I. and Sinclair, T., Omitting types in operator systems, Indiana Univ. Math. J. 66 (2017), 821–844.CrossRefGoogle Scholar
Goldbring, I. and Sinclair, T., Robinson forcing and the quasidiagonality problem, Int. J. Math. 28 (2017), 1750008.CrossRefGoogle Scholar
Haagerup, U., Quasitraces on exact C∗ -algebras are traces, C. R. Math. Acad. Sci. Soc. R. Can. 36 (2014), 67–92.Google Scholar
Hart, B., Continuous model theory course notes, available at http://ms.mcmaster.ca/∼bradd/courses/math712/index.html.Google Scholar
Hart, K. P., There is no categorical metric continuum, Aportaciones Mat. Investig. 19 (2007), 39–43.Google Scholar
Hodges, W., Building Models by Games, London Mathematical Society Student Texts, vol. 2 (Cambridge University Press, Cambridge, 1985).Google Scholar
Junge, M. and Pisier, G., Bilinear forms on exact operator spaces and 𝓑(H) ⊗𝓑 (H), Geom. Funct. Anal. 5 (1995), 329–363.CrossRefGoogle Scholar
Lewis, W., The pseudo-arc, Bol. Soc. Mat. Mexicana (3) 5 (1999), 25–77.Google Scholar
Lupini, M., Uniqueness, universality, and homogeneity of the noncommutative Gurarij space, Adv. Math. 298 (2016), 286–324.CrossRefGoogle Scholar
Tikuisis, A., White, S. and Winter, W., Quasidiagonality of nuclear C ∗ -algebras, Ann. of Math. 185 (2017), 229–284.CrossRefGoogle Scholar
Toms, A. S. and Winter, W., Strongly self-absorbing C ∗ -algebras, Trans. Amer. Math. Soc. 359 (2007), 3999–4029.CrossRefGoogle Scholar