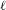Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-22T16:28:37.920Z Has data issue: false hasContentIssue false
  • English
  • Français

THE $\ell$-MODULAR LOCAL LANGLANDS CORRESPONDENCE AND LOCAL CONSTANTS

Part of: Discontinuous groups and automorphic forms Lie groups

Published online by Cambridge University Press:  08 November 2019

R. Kurinczuk Open the ORCID record for R. Kurinczuk [Opens in a new window]  and
N. Matringe
R. Kurinczuk
Affiliation:
Department of Mathematics, Imperial College London, SW7 2AZ, UK ([email protected])
N. Matringe
Affiliation:
Université de Poitiers, Laboratoire de Mathématiques et Applications, Téléport 2 - BP 30179, Boulevard Marie et Pierre Curie, 86962, Futuroscope Chasseneuil Cedex, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $F$ be a non-archimedean local field of residual characteristic 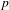$p$, 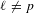$\ell \neq p$ be a prime number, and 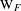$\text{W}_{F}$ the Weil group of $F$. We classify equivalence classes of 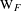$\text{W}_{F}$-semisimple Deligne 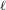$\ell$-modular representations of 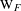$\text{W}_{F}$ in terms of irreducible 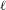$\ell$-modular representations of 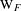$\text{W}_{F}$, and extend constructions of Artin–Deligne local constants to this setting. Finally, we define a variant of the 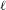$\ell$-modular local Langlands correspondence which satisfies a preservation of local constants statement for pairs of generic representations.

Keywords

modular local Langlands correspondenceDeligne representationslocal constants

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 5 , September 2021 , pp. 1585 - 1635
Check for updates
Copyright
© Cambridge University Press 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubert, A.-M., Dualité dans le groupe de Grothendieck de la catégorie des représentations lisses de longueur finie d’un groupe réductif p-adique, Trans. Amer. Math. Soc. 347(6) (1995), 2179–2189.Google Scholar
Bernstein, I. N. and Zelevinsky, A. V., Induced representations of reductive p-adic groups. I, Ann. Sci. Éc. Norm. Supér. (4) 10(4) (1977), 441–472.CrossRefGoogle Scholar
Bushnell, C. J. and Henniart, G., The local Langlands conjecture for GL(2), Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 335 (Springer-Verlag, Berlin, 2006).CrossRefGoogle Scholar
Bushnell, C. J. and Henniart, G., Modular local Langlands correspondence for GLn , Int. Math. Res. Not. IMRN 2014(15) (2014), 4124–4145.CrossRefGoogle Scholar
Dat, J.-F., Lefschetz operator and local Langlands mod ℓ: the regular case, Nagoya Math. J. 208 (2012), 1–38.CrossRefGoogle Scholar
Dat, J.-F., Lefschetz operator and local Langlands modulo ℓ: the limit case, Algebra Number Theory 8(3) (2014), 729–766.CrossRefGoogle Scholar
Deligne, P., Formes modulaires et représentations de GL(2), in Modular Functions of One Variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, volume 349, pp. 55–105. (1973).CrossRefGoogle Scholar
Deligne, P., Les constantes des équations fonctionnelles des fonctions L, in Modular Functions of One Variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Mathematics, volume 349, pp. 501–597 (Springer, Berlin, 1973).CrossRefGoogle Scholar
Emerton, M. and Helm, D., The local Langlands correspondence for GLn in families, Ann. Sci. Éc. Norm. Supér. (4) 47(4) (2014), 655–722.CrossRefGoogle Scholar
Helm, D., On the modified mod p local Langlands correspondence for GL2(ℚℓ), Math. Res. Lett. 20(3) (2013), 489–500.CrossRefGoogle Scholar
Helm, D. and Moss, G., Gamma factors in deformation rings, preprint, 2017, arXiv:1510.08743v2.Google Scholar
Kurinczuk, R. and Matringe, N., Rankin-Selberg local factors modulo ℓ, Selecta Math. (N.S.) 23(1) (2017), 767–811.CrossRefGoogle Scholar
Mínguez, A., Fonctions zêta ℓ-modulaires, Nagoya Math. J. 208 (2012), 39–65.CrossRefGoogle Scholar
Mínguez, A. and Sécherre, V., Représentations lisses modulo ℓ de GLm(D), Duke Math. J. 163(4) (2014), 795–887.CrossRefGoogle Scholar
Mínguez, A. and Sécherre, V., L’involution de Zelevinski modulo ℓ , Represent. Theory 19 (2015), 236–262.CrossRefGoogle Scholar
Rohrlich, D. E., Elliptic curves and the Weil-Deligne group, in Elliptic Curves and Related Topics, CRM Proceedings & Lecture Notes, volume 4, pp. 125–157 (American Mathematical Society, Providence, RI, 1994).CrossRefGoogle Scholar
Serre, J.-P., Sur la semi-simplicité des produits tensoriels de représentations de groupes, Invent. Math. 116(1-3) (1994), 513–530.CrossRefGoogle Scholar
Tate, J. T., Fourier analysis in number fields, and Hecke’s zeta-functions, in Algebraic Number Theory (Proc. Instructional Conf., Brighton, 1965), pp. 305–347 (Thompson, Washington, DC, 1967).Google Scholar
Vignéras, M.-F., Représentations ℓ-modulaires d’un groupe réductif p-adique avec ℓ≠p, Progress in Mathematics, Volume 137 (Birkhäuser Boston Inc., Boston, MA, 1996).Google Scholar
Vignéras, M.-F., à propos d’une conjecture de Langlands modulaire, in Finite Reductive Groups (Luminy, 1994), Progress in Mathematics, Volume 141, pp. 415–452 (Birkhäuser Boston, Boston, MA, 1997).Google Scholar
Vignéras, M.-F., Cohomology of sheaves on the building and R-representations, Invent. Math. 127(2) (1997), 349–373.Google Scholar
Vignéras, M.-F., Induced R-representations of p-adic reductive groups, Selecta Math. (N.S.) 4(4) (1998), 549–623.CrossRefGoogle Scholar
Vignéras, M.-F., Congruences modulo ℓ between 𝜖 factors for cuspidal representations of GL(2), J. Théor. Nombres Bordeaux 12(2) (2000), 571–580. Colloque International de Théorie des Nombres (Talence, 1999).CrossRefGoogle Scholar
Vignéras, M.-F., Correspondance de Langlands semi-simple pour GL(n, F) modulo l ≠ p, Invent. Math. 144(1) (2001), 177–223.CrossRefGoogle Scholar
Vignéras, M.-F., La conjecture de Langlands locale pour GL(n, F) modulo l quand l ≠ p, l > n, Ann. Sci. Éc. Norm. Supér. (4) 34(6) (2001), 789–816.CrossRefGoogle Scholar
Vignéras, M.-F., On highest Whittaker models and integral structures, in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 773–801 (Johns Hopkins Univ. Press, Baltimore, MD, 2004).Google Scholar
Zelevinsky, A. V., Induced representations of reductive p-adic groups. II. On irreducible representations of GL(n), Ann. Sci. Éc. Norm. Supér. (4) 13(2) (1980), 165–210.CrossRefGoogle Scholar