Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-04T21:03:34.537Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ELEMENTARY THEORY OF LARGE FIELDS OF TOTALLY 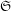$\mathfrak{S}$ -ADIC NUMBERS

Published online by Cambridge University Press:  23 April 2015

Arno Fehm
Arno Fehm*
Affiliation:
University of Konstanz, Department of Mathematics and Statistics, 78457 Konstanz, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze the elementary theory of certain fields 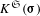$K^{\mathfrak{S}}(\boldsymbol{\unicode[STIX]{x1D70E}})$ of totally 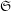$\mathfrak{S}$ -adic algebraic numbers that were introduced and studied by Geyer and Jarden and by Haran, Jarden, and Pop. In particular, we provide an axiomatization of these theories and prove their decidability, thereby giving a common generalization of classical decidability results of Jarden and Kiehne, Fried, Haran, and Völklein, and Ershov.

Keywords

totally S-adic numbersabsolute Galois groupmodel theory of profinite groupsdecidability of fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 1 , February 2017 , pp. 121 - 154
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Basarab, S. A., The absolute Galois group of a pseudo real closed field with finitely many orders, J. Pure Appl. Algebra 38 (1985), 1–18.CrossRefGoogle Scholar
Chatzidakis, Z., Model theory of profinite groups, PhD thesis, Yale University (1984).Google Scholar
Chatzidakis, Z., Model theory of profinite groups having the Iwasawa property, Illinois J. Math. 42(1) (1998), 70–96.CrossRefGoogle Scholar
Chatzidakis, Z., Properties of forking in 𝜔-free pseudo-algebraically closed fields, J. Symbolic Logic 67(3) (2002), 957–996.CrossRefGoogle Scholar
Cherlin, G., van den Dries, L. and Macintyre, A., Decidability and undecidability theorems for PAC-fields, Bull. Amer. Math. Soc. 4(1) (1981), 101–104.CrossRefGoogle Scholar
Cherlin, G., van den Dries, L. and Macintyre, A., The elementary theory of regularly closed fields, Manuscript (1982).Google Scholar
Engler, A. J. and Prestel, A., Valued Fields (Springer, 2005).Google Scholar
Ershov, Y., PC p -fields with universal Galois group, Siberian Adv. Math. 1(4) (1991), 1–26.Google Scholar
Ershov, Y., Fields with continuous local elementary properties II, Algebra Logic 34(3) (1995), 140–146.CrossRefGoogle Scholar
Ershov, Y., Free 𝛥∗ -groups, Algebra Logic 35(2) (1996), 86–95.CrossRefGoogle Scholar
Ershov, Y., Nice local–global fields I, Algebra Logic 35(4) (1996), 229–235.CrossRefGoogle Scholar
Ershov, Y., Uniformly small 𝛥∗ -groups, Algebra Logic 38(1) (1999), 12–20.CrossRefGoogle Scholar
Fehm, A., Decidability of large fields of algebraic numbers, PhD thesis, Tel Aviv University (2010).Google Scholar
Fehm, A., Elementary geometric local–global principles for fields, Ann. Pure Appl. Logic 164(10) (2013), 989–1008.CrossRefGoogle Scholar
Fried, M. D., Haran, D. and Völklein, H., Real Hilbertianity and the field of totally real numbers, in Arithmetic Geometry (ed. Childress, N. and Jones, J. W.), Contemporary Mathematics, Volume 174, pp. 1–34 (American Mathematical Society, 1994).CrossRefGoogle Scholar
Fried, M. D. and Jarden, M., Field Arithmetic, third edn (Springer, 2008).Google Scholar
Frohn, N., Model theory of absolute Galois groups, PhD thesis, University of Freiburg (Breisgau) (2010).Google Scholar
Geyer, W.-D. and Jarden, M., PSC Galois extensions of Hilbertian fields, Math. Nachr. 236(1) (2002), 119–160.3.0.CO;2-U>CrossRefGoogle Scholar
Haran, D., The undecidability of real closed fields, Manuscripta Math. 49 (1984), 91–108.CrossRefGoogle Scholar
Haran, D., Jarden, M. and Pop, F., The absolute Galois group of the field of totally S-adic numbers, Nagoya Math. J. 194 (2009), 91–147.CrossRefGoogle Scholar
Haran, D., Jarden, M. and Pop, F., The absolute Galois group of subfields of the field of totally S-adic numbers, Funct. Approx. Comment. Math. 46(2) (2012), 205–223.CrossRefGoogle Scholar
Jarden, M., Totally $S$ -adic extensions of Hilbertian fields, Manuscript (1995).Google Scholar
Jarden, M. and Kiehne, U., The elementary theory of algebraic fields of finite corank, Invent. Math. 30(3) (1975), 275–294.CrossRefGoogle Scholar
Jarden, M. and Ritter, J., On the characterization of local fields by their absolute Galois groups, J. Number Theory 11(1) (1979), 1–13.CrossRefGoogle Scholar
Jarden, M. and Razon, A., Rumely’s local global principle for algebraic PSC fields over rings, Trans. Amer. Math. Soc. 350(1) (1998), 55–85.CrossRefGoogle Scholar
Koenigsmann, J., From p-rigid elements to valuations (with a Galois-characterization of p-adic fields), J. Reine Angew. Math. 465 (1995), 165–182.Google Scholar
Lam, T. Y., Quadratic Forms over Fields (Springer, 2004).Google Scholar
Lang, S., Algebra, third edn (Springer, 2002).CrossRefGoogle Scholar
Marker, D., Model Theory: An Introduction (Springer, 2002).Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, second edn (Springer, 2008).CrossRefGoogle Scholar
Pop, F., Galoissche Kennzeichnung p-adisch abgeschlossener Körper, PhD Thesis, Heidelberg (1986).Google Scholar
Prestel, A. and Roquette, P., Formally p-adic Fields (Springer, 1984).CrossRefGoogle Scholar
Prestel, A., Lectures on Formally Real Fields (Springer, 1984).CrossRefGoogle Scholar
Rumely, R. S., Undecidability and definability for the theory of global fields, Trans. Amer. Math. Soc. 262(1) (1980), 195–217.CrossRefGoogle Scholar
Ribes, L. and Zalesskii, P., Profinite Groups (Springer, 2000).CrossRefGoogle Scholar
Shlapentokh, A., Hilbert’s Tenth Problem: Diophantine Classes and Extensions to Global Fields (Cambridge University Press, 2007).Google Scholar