Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T17:43:56.136Z Has data issue: false hasContentIssue false
  • English
  • Français

THE DISTRIBUTION OF TORSION SUBSCHEMES OF ABELIAN VARIETIES

Part of: Algebraic groups Abelian varieties and schemes Arithmetic problems. Diophantine geometry

Published online by Cambridge University Press:  15 December 2014

Jeffrey D. Achter Open the ORCID record for Jeffrey D. Achter [Opens in a new window]
Jeffrey D. Achter*
Affiliation:
Department of Mathematics, Colorado State University, Fort Collins, CO 80523, USA ([email protected]) URL http://www.math.colostate.edu/∼achter
Get access Rights & Permissions [Opens in a new window]

Abstract

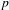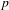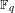We consider the distribution of $p$-power group schemes among the torsion of abelian varieties over finite fields of characteristic $p$, as follows. Fix natural numbers $g$ and $n$, and let ${\it\xi}$ be a non-supersingular principally quasipolarized Barsotti–Tate group of level $n$. We classify the $\mathbb{F}_{q}$-rational forms 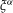${\it\xi}^{{\it\alpha}}$ of ${\it\xi}$. Among all principally polarized abelian varieties 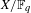$X/\mathbb{F}_{q}$ of dimension $g$ with 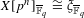$X[p^{n}]_{\bar{\mathbb{F}}_{q}}\cong {\it\xi}_{\bar{\mathbb{F}}_{q}}$, we compute the frequency with which 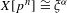$X[p^{n}]\cong {\it\xi}^{{\it\alpha}}$. The error in our estimate is bounded by 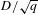$D/\sqrt{q}$, where 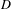$D$ depends on $g$, $n$, and 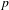$p$, but not on ${\it\xi}$.

Keywords

abelian varietygroup schemearithmetic statistics

MSC classification

Primary: 14G17: Positive characteristic ground fields 14K10: Algebraic moduli, classification 14L05: Formal groups, $p$-divisible groups 14L15: Group schemes
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 4 , October 2016 , pp. 693 - 710
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achter., J. D., Results of Cohen-Lenstra type for quadratic function fields, in Computational Arithmetic Geometry, Contemporary Mathematics, Volume 463, pp. 1–7 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Achter, J. D. and Pries, R., Monodromy of the p-rank strata of the moduli space of curves, Int. Math. Res. Not. IMRN(15: Art. ID rnn053) (2008), 25.Google Scholar
Achter, J. D. and Pries, R., The p-rank strata of the moduli space of hyperelliptic curves, Adv. Math. 227(5) (2011), 1846–1872.Google Scholar
Achter, J. D. and Pries, R., Generic Newton polygons for curves of given p-rank, in Algebraic Curves and Finite Fields: Cryptography and Other Applications, Radon Series on Computational and Applied Mathematics, Volume 16, pp. 1–22 (de Gruyter, Boston and Berlin, 2014).Google Scholar
Cais, B., Ellenberg, J. S. and Zureick-Brown, D., Random Dieudonné modules, random p-divisible groups, and random curves over finite fields, J. Inst. Math. Jussieu 12(3) (2013), 651–676.Google Scholar
Castryck, W., Folsom, A., Hubrechts, H. and Sutherland, A. V., The probability that the number of points on the Jacobian of a genus 2 curve is prime, Proc. Lond. Math. Soc. (3) 104(6) (2012), 1235–1270.Google Scholar
Chai, C.-L., Monodromy of Hecke-invariant subvarieties, Pure Appl. Math. Q. 1(2) (2005), 291–303.Google Scholar
Chai, C.-L. and Oort, F., Monodromy and irreducibility of leaves, Ann. of Math. (2) 173(3) (2011), 1359–1396.Google Scholar
Cohen, H. and Lenstra , H. W. Jr, Heuristics on class groups of number fields, in Number Theory, Noordwijkerhout 1983 (Noordwijkerhout, 1983), Lecture Notes in Mathematics, Volume 1068, pp. 33–62 (Springer, Berlin, 1984).Google Scholar
Ekedahl, T., The action of monodromy on torsion points of Jacobians, in Arithmetic Algebraic Geometry (Texel, 1989), pp. 41–49 (Birkhäuser, Boston, Boston, MA, 1991).Google Scholar
Ekedahl, T. and van der Geer, G., Cycle classes of the E-O stratification on the moduli of abelian varieties, in Algebra, Arithmetic, and Geometry: in Honor of Yu. I. Manin. Vol. I, Progress in Mathematics, Volume 269, pp. 567–636 (Birkhäuser, Boston Inc., Boston, MA, 2009).CrossRefGoogle Scholar
Ellenberg, J., Venkatesh, A. and Westerland, C., Homological stability for Hurwitz spaces and the Cohen–Lenstra conjecture over function fields, December 2009,arXiv:0912.0325.Google Scholar
Faltings, G. and Chai, C.-L., Degeneration of Abelian Varieties (Springer-Verlag, Berlin, 1990). With an appendix by David Mumford.CrossRefGoogle Scholar
Gabber, O. and Vasiu, A., Dimensions of group schemes of automorphisms of truncated Barsotti–Tate groups, Int. Math. Res. Not. IMRN 18 (2013), 4285–4333.Google Scholar
Garuti, M. A., Barsotti–Tate groups and p-adic representations of the fundamental group scheme., Math. Ann. 341(3) (2008), 603–622.Google Scholar
Harashita, S., Generic Newton polygons of Ekedahl–Oort strata: Oort’s conjecture, Ann. Inst. Fourier (Grenoble) 60(5) (2010), 1787–1830.Google Scholar
Illusie, L., Déformations de groupes de Barsotti-Tate (d’après A. Grothendieck), Astérisque 127 (1985), 151–198. Seminar on arithmetic bundles: the Mordell conjecture (Paris, 1983/84).Google Scholar
Katz, N. M. and Sarnak, P., Random Matrices, Frobenius Eigenvalues, and Monodromy (American Mathematical Society, Providence, RI, 1999).Google Scholar
Kowalski, E., The large sieve, monodromy and zeta functions of curves, J. Reine Angew. Math. 601 (2006), 29–69.Google Scholar
Lau, E., Nicole, M.-H. and Vasiu, A., Stratifications of Newton polygon strata and Traverso’s conjectures for p-divisible groups, Ann. of Math. (2) 178(3) (2013), 789–834.Google Scholar
Liedtke, C., The p-torsion subgroup scheme of an elliptic curve, J. Number Theory 131(11) (2011), 2064–2077.Google Scholar
Moonen, B., Group schemes with additional structures and Weyl group cosets, in Moduli of Abelian Varieties (Texel Island, 1999), pp. 255–298 (Birkhäuser, Basel, 2001).Google Scholar
Oort, F., Foliations in moduli spaces of abelian varieties, J. Amer. Math. Soc. 17(2) (2004), 267–296 (electronic).Google Scholar
Oort, F., Minimal p-divisible groups, Ann. of Math. (2) 161(2) (2005), 1021–1036.Google Scholar
Serre, J.-P., Zeta and L functions, in Arithmetical Algebraic Geometry (Proc. Conf. Purdue Univ., 1963, pp. 82–92 (Harper & Row, New York, 1965).Google Scholar
Serre, J.-P., Galois cohomology, in Springer Monographs in Mathematics, English edition (Springer-Verlag, Berlin, 2002). Translated from the French by Patrick Ion and revised by the author.Google Scholar
Vasiu, A., Level m stratifications of versal deformations of p-divisible groups, J. Algebraic Geom. 17(4) (2008), 599–641.Google Scholar
Wedhorn, T., The dimension of Oort strata of Shimura varieties of PEL-type, in Moduli of Abelian Varieties (Texel Island, 1999), pp. 441–471 (Birkhäuser, Basel, 2001).Google Scholar