Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-05T00:46:07.820Z Has data issue: false hasContentIssue false
  • English
  • Français

DIFFERENTIAL OPERATORS ON 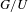$G/U$ AND THE AFFINE GRASSMANNIAN

Published online by Cambridge University Press:  07 April 2014

Victor Ginzburg  and
Simon Riche
Victor Ginzburg
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA ([email protected]) Université Blaise Pascal - Clermont-Ferrand II, Laboratoire de Mathématiques, CNRS, UMR 6620, Campus universitaire des Cézeaux, F-63177 Aubière Cedex, France ([email protected])
Simon Riche
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA ([email protected]) Université Blaise Pascal - Clermont-Ferrand II, Laboratoire de Mathématiques, CNRS, UMR 6620, Campus universitaire des Cézeaux, F-63177 Aubière Cedex, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the equivariant cohomology of cofibers of spherical perverse sheaves on the affine Grassmannian of a reductive algebraic group in terms of the geometry of the Langlands dual group. In fact we give two equivalent descriptions: one in terms of 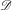$\mathscr{D}$-modules of the basic affine space, and one in terms of intertwining operators for universal Verma modules. We also construct natural collections of isomorphisms parameterized by the Weyl group in these three contexts, and prove that they are compatible with our isomorphisms. As applications we reprove some results of the first author and of Braverman and Finkelberg.

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 14 , Issue 3 , July 2015 , pp. 493 - 575
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achar, P. N., Henderson, A. and Riche, S., Geometric Satake, Springer correspondence, and small representations II, preprint arXiv:1205.5089 (2012).Google Scholar
Achar, P. N. and Riche, S., Constructible sheaves on affine Grassmannians and geometry of the dual nilpotent cone, Israel J. Math. (2011), preprint arXiv:1102.2821 (to appear).Google Scholar
Arkhipov, S., Bezrukavnikov, R. and Ginzburg, V., Quantum groups, the loop Grassmannian, and the Springer resolution, J. Amer. Math. Soc. 17 (2004), 595–678.Google Scholar
Artin, M., Tate, J. and Van den Bergh, M., Some algebras associated to automorphisms of elliptic curves, in The Grothendieck Festschrift, Vol. I, Progr. Math., Volume 86, pp. 33–85 (Birkhäuser, 1990).Google Scholar
Baumann, P., Propriétés et combinatoire des bases de type canonique, mémoire d’habilitation, available on http://tel.archives-ouvertes.fr/tel-00705204.Google Scholar
Beilinson, A. and Drinfeld, V., Quantization of Hitchin’s integrable system and Hecke eigensheaves, preprint available at http://www.math.uchicago.edu/∼mitya/langlands.html.Google Scholar
Bernstein, I., Gel’fand, I. and Gel’fand, S., Differential operators on the base affine space and a study of g-modules, in Lie Groups and Their Representations (Proc. Summer School, Bolyai János Math. Soc., Budapest, 1971), pp. 21–64 (Halsted, 1975).Google Scholar
Bezrukavnikov, R., Braverman, A. and Positselskii, L., Gluing of abelian categories and differential operators on the basic affine space, J. Inst. Math. Jussieu 1 (2002), 543–557.Google Scholar
Bezrukavnikov, R. and Finkelberg, M., Equivariant Satake category and Kostant–Whittaker reduction, Mosc. Math. J. 8 (2008), 39–72.Google Scholar
Bezrukavnikov, R., Finkelberg, M. and Mirković, I., Equivariant homology and K-theory of affine Grassmannians and Toda lattices, Compos. Math. 141 (2005), 746–768.Google Scholar
Bezrukavnikov, R. and Riche, S., Affine braid group actions on Springer resolutions, Ann. Sci. Éc. Norm. Supér. 45 (2012), 535–599.Google Scholar
Braverman, A. and Finkelberg, M., Dynamical Weyl groups and equivariant cohomology of transversal slices in affine Grassmannians, Math. Res. Lett. 18 (2011), 505–512.Google Scholar
Brion, M. and Kumar, S., Frobenius splitting methods in geometry and representation theory, Progr. Math., Volume 231 (Birkhäuser, 2004).Google Scholar
Broer, B., Line bundles on the cotangent bundle of the flag variety, Invent. Math. 113 (1993), 1–20.Google Scholar
Brylinski, R., Limits of weight spaces, Lusztig’s q-analogs, and fiberings of adjoint orbits, J. Amer. Math. Soc. 2 (1989), 517–533.Google Scholar
Brylinski, J. L., Malgrange, B. and Verdier, J. L., Transformation de Fourier géométrique. II, C. R. Acad. Sci. Paris Sér. I Math. 303 (1986), 193–198.Google Scholar
Deligne, P. and Milne, J., Tannakian categories, in Hodge Cycles, Motives, and Shimura Varieties, Lecture Notes in Math., Volume 900 (Springer, 1982).Google Scholar
Dodd, C., Equivariant coherent sheaves, Soergel bimodules, and categorification of affine Hecke algebras, preprint arXiv:1108.4028 (2011).Google Scholar
Etingof, P. and Varchenko, A., Dynamical Weyl groups and applications, Adv. Math. 167 (2002), 74–127.Google Scholar
Evens, S. and Mirković, I., Fourier transform and the Iwahori–Matsumoto involution, Duke Math. J. 86 (1997), 435–464.CrossRefGoogle Scholar
Fiebig, P. and Williamson, G., Parity sheaves, moment graphs and the $p$-smooth locus of Schubert varieties, Ann. Inst. Fourier (Grenoble), preprint arXiv:1008.0719, 2010 (to appear).Google Scholar
Ginzburg, V., Perverse sheaves on a loop group and Langlands’ duality, preprint arXiv:alg-geom/9511007 (1995).Google Scholar
Ginzburg, V., Variations on themes of Kostant, Transform. Groups 13 (2008), 557–573.Google Scholar
Ginzburg, V. and Kazhdan, D., A class of symplectic varieties associated with the space $G/U$ (in preparation).Google Scholar
Humphreys, J. E., Representations of Semisimple Lie Algebras in the BGG Category O, Graduate Studies in Mathematics, Volume 94 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Jantzen, J. C., Representations of algebraic groups, second edition, Mathematical Surveys and Monographs, Volume 107 (Amer. Math. Soc., 2003).Google Scholar
Jantzen, J. C., Nilpotent orbits in representation theory, in Lie theory, Progr. Math., Volume 228, pp. 1–211 (Birkhäuser, 2004).CrossRefGoogle Scholar
Kashiwara, M., The universal Verma module and the b-function, in Algebraic Groups and Related Topics (Kyoto/Nagoya, 1983), Adv. Stud. Pure Math., Volume 6, pp. 67–81 (North-Holland, 1985).CrossRefGoogle Scholar
Kazhdan, D. and Laumon, G., Gluing of perverse sheaves and discrete series representation, J. Geom. Phys. 5 (1988), 63–120.Google Scholar
Kazhdan, D. and Lusztig, G., Schubert varieties and Poincaré duality, in Geometry of the Laplace operator (Proc. Sympos. Pure Math., Univ. Hawaii, Honolulu, Hawaii, 1979), Proc. Sympos. Pure Math., Volume XXXVI, pp. 185–203 (Amer. Math. Soc., 1980).Google Scholar
Kostant, B., The principal three-dimensional subgroup and the Betti numbers of a complex simple Lie group, Amer. J. Math. 81 (1959), 973–1032.Google Scholar
Levasseur, T. and Stafford, J. T., Differential operators and cohomology groups on the basic affine space, in Studies in Lie Theory, Progr. Math., Volume 243, pp. 377–403 (Birkhäuser, 2006).Google Scholar
Lusztig, G., Cuspidal local systems and graded Hecke algebras. I, Inst. Hautes Études Sci. Publ. Math. 67 (1988), 145–202.CrossRefGoogle Scholar
Matsumura, H., Commutative Ring Theory (Cambridge University Press, 1986).Google Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. 166 (2007), 95–143.CrossRefGoogle Scholar
Ngô, B. C. and Polo, P., Résolutions de Demazure affines et formule de Casselman–Shalika géométrique, J. Algebraic Geom. 10 (2001), 515–547.Google Scholar
Shapovalov, N., Structure of the algebra of differential operators on the basic affine space, Funct. Anal. Appl. 8 (1974), 37–46.Google Scholar
Springer, T., Quelques applications de la cohomologie d’intersection, Astérisque 92–93 (1982), 249–273.Google Scholar
Tarasov, V. and Varchenko, A., Difference equations compatible with trigonometric KZ differential equations, Int. Math. Res. Not. 2000(15) 801–829.Google Scholar
Vasserot, E., On the action of the dual group on the cohomology of perverse sheaves on the affine Grassmannian, Compos. Math. 131 (2002), 51–60.CrossRefGoogle Scholar
Yekutieli, A. and Zhang, J. J., Dualizing complexes and tilting complexes over simple rings, J. Algebra 256 (2002), 556–567.Google Scholar
Yun, Z. and Zhu, X., Integral homology of loop groups via Langlands dual group, Represent. Theory 15 (2011), 347–369.Google Scholar