Hostname: page-component-5cf477f64f-r2nwp Total loading time: 0 Render date: 2025-04-02T11:25:08.445Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential graded motives: weight complex, weight filtrations and spectral sequences for realizations; Voevodsky versus Hanamura

Part of: Singularities Higher algebraic $K$-theory Homological methods (Co)homology theory

Published online by Cambridge University Press:  16 October 2008

M. V. Bondarko
M. V. Bondarko
Affiliation:
Saint-Petersburg State University, Faculty of Higher Algebra and Number Theory, Bibliotechnaya Pl. 2, 198904, Saint Petersburg, Russia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

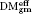We describe explicitly the Voevodsky's triangulated category of motives (and give a ‘differential graded enhancement’ of it). This enables us to able to verify that DMgm ℚ is (anti)isomorphic to Hanamura's (k).

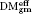We obtain a description of all subcategories (including those of Tate motives) and of all localizations of . We construct a conservative weight complex functor 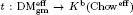; t gives an isomorphism 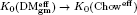. A motif is mixed Tate whenever its weight complex is. Over finite fields the Beilinson–Parshin conjecture holds if and only if tℚ is an equivalence.

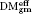For a realization D of we construct a spectral sequence S (the spectral sequence of motivic descent) converging to the cohomology of an arbitrary motif X. S is ‘motivically functorial’; it gives a canonical functorial weight filtration on the cohomology of D(X). For the ‘standard’ realizations this filtration coincides with the usual one (up to a shift of indices). For the motivic cohomology this weight filtration is non-trivial and appears to be quite new.

We define the (rational) length of a motif M; modulo certain ‘standard’ conjectures this length coincides with the maximal length of the weight filtration of the singular cohomology of M.

Keywords

motivesalgebraic cyclesrealizations and cohomologyweight filtrations and spectral sequences

MSC classification

Secondary: 14F42: Motivic cohomology; motivic homotopy theory 16E45: Differential graded algebras and applications 14F20: Étale and other Grothendieck topologies and (co)homologies 19D55: $K$-theory and homology; cyclic homology and cohomology 32S20: Global theory of singularities; cohomological properties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 8 , Issue 1 , January 2009 , pp. 39 - 97
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Balmer, P. and Schlichting, M., Idempotent completion of triangulated categories, J. Alg. 236(2) (2001), 819–834.CrossRefGoogle Scholar
2.Barbieri-Viale, L., Rosenschon, A. and Saito, M., Deligne's conjecture on 1-motives, Annals Math. 158(2) (2003), 593–633.CrossRefGoogle Scholar
3.Beilinson, A. and Vologodsky, V., A DG guide to Voevodsky's motives, Geom. Funct. Analysis 17 (2007), 1709–1787.CrossRefGoogle Scholar
4.Bloch, S., The moving lemma for higher Chow groups, J. Alg. Geom. 3(3) (1994), 537–568.Google Scholar
5.Bloch, S. and Esnault, H., Künneth projectors for open varieties, preprint (available at http://arxiv.org/abs/math.AG/0502447, 2005).Google Scholar
6.Bondal, A. I. and Kapranov, M. M., Enhanced triangulated categories, Mat. Sb. 181(5) (1990), 669–683 (in Russian; English transl. Math. USSR Sb. 70(1) (1991), 93–107).Google Scholar
7.Bondarko, M., Weight structures vs. t-structures; weight filtrations, spectral sequences, and complexes (for motives and in general), preprint (available at http://arxiv.org/abs/0704.4003, 2007).Google Scholar
8.de Jong, A. J., Smoothness, semi-stability and alterations, Publ. Math. IHES 83 (1996), 51–93.CrossRefGoogle Scholar
9.Deglise, F., Around the Gysin triangle, preprint (available at http://www.math.uiuc.edu/K-theory/0764/, 2005).Google Scholar
10.Drinfeld, V., DG quotients of DG categories, J. Alg. 272 (2004), 643–691.CrossRefGoogle Scholar
11.Friedlander, E. and Suslin, A., The spectral sequence relating algebraic K-theory to the motivic cohomology, Annales Scient. Éc. Norm. Sup. 35 (2002), 773–875.CrossRefGoogle Scholar
12.Friedlander, E. and Voevodsky, V., Bivariant cycle cohomology, in Cycles, transfers and motivic homology theories (ed. Voevodsky, V., Suslin, A. and Friedlander, E.), Annals of Mathematical Studies, Volume 143, pp. 138–187 (Princeton University Press, 2000).Google Scholar
13.Gelfand, S. and Manin, Yu., Methods of homological algebra, 2nd edn, Springer Mono graphs in Mathematics (Springer, 2003).CrossRefGoogle Scholar
14.Gillet, H. and Soulé, C., Descent, motives and K-theory, J. Reine Angew. Math. 478 (1996), 127–176.Google Scholar
15.Gillet, H. and Soulé, C., Weight complexes for arithmetic varieties, unpublished (available at http://www.math.uic.edu/~henri/weightcomplexes_slides.pdf).Google Scholar
16.Guillen, F. and Aznar, V. Navarro, Un critère d'extension des foncteurs définis sur les schémas lisses, Publ. Math. IHES 95 (2002), 1–91.CrossRefGoogle Scholar
17.Hanamura, M., Mixed motives and algebraic cycles, I, Math. Res. Lett. 2 (1995), 811–821.CrossRefGoogle Scholar
18.Hanamura, M., Mixed motives and algebraic cycles, III, Math. Res. Lett. 6 (1999), 61–82.CrossRefGoogle Scholar
19.Hanamura, M., Homological and cohomological motives of algebraic varieties, Invent. Math. 142 (2000), 319–349.CrossRefGoogle Scholar
20.Hanamura, M., Mixed motives and algebraic cycles, II, Invent. Math. 158 (2004), 105–179.CrossRefGoogle Scholar
21.Huber, A., Realizations of Voevodsky's motives, J. Alg. Geom. 9(4) (2000), 755–799.Google Scholar
22.Huber, A. and Kahn, B., The slice filtration and mixed Tate motives, Compositio Math. 142(4) (2006), 907–936.CrossRefGoogle Scholar
23.Jannsen, U., Motives, numerical equivalence and semi-simplicity, Invent. Math. 107 (1992), 447–452.CrossRefGoogle Scholar
24.Kahn, B., Algebraic K-theory, algebraic cycles and arithmetic geometry, in K-theory handbook, Volume 1, pp. 351–428 (Springer, 2005).CrossRefGoogle Scholar
25.Kriz, I. and May, J., Operads, algebras, modules and motives, Astérisque, No. 233 (Société Mathématique de France, Paris, 1995).Google Scholar
26.Levine, M., Bloch's higher Chow groups revisited, Astérisque 226(10) (1994), 235–320.Google Scholar
27.Levine, M., Mixed motives, Mathematical Surveys and Monographs, Volume 57 (American Mathemetical Society, Providence, RI, 1998).CrossRefGoogle Scholar
28.Levine, M., Mixed motives, in K-theory handbook, Volume 1, pp. 429–521 (Springer, 2005).CrossRefGoogle Scholar
29.Levine, M., Smooth motives, preprint (available at http://arxiv.org/abs/0807.2265).Google Scholar
30.Mazza, C., Voevodsky, V. and Weibel, Ch., Lecture notes on motivic cohomology, Clay Mathematics Monographs, Volume 2 (American Mathemetical Society, Providence, RI, 2006).Google Scholar
31.Milne, J. and Ramachandran, N., Motivic complexes over a finite field and the ring of correspondences at the generic point, preprint (available at http://www.jmilne.org/math/preprints/iso3.pdf, 2005).Google Scholar
32.Spitzweck, M., Some constructions for Voevodsky's triangulated categories of motives, preprint.Google Scholar
33.Suslin, A., On the Grayson spectral sequence, Tr. Mat. Inst. Steklova 241 (2003), 218–253 (English transl. Proc. Steklov Inst. Math. 241(2) (2003), 202–237).Google Scholar
34.Voevodsky, V., Homology of schemes, Selecta Math. 2(1) (1996), 111–153.CrossRefGoogle Scholar
35.Voevodsky, V., Cohomological theory of presheaves with transfers, in Cycles, transfers and motivic homology theories (ed. Voevodsky, V., Suslin, A. and Friedlander, E.), Annals of Mathematical Studies, Volume 143, pp. 87–137 (Princeton University Press, 2000).Google Scholar
36.Voevodsky, V., Triangulated category of motives, in Cycles, transfers and motivic homology theories (ed. Voevodsky, V., Suslin, A. and Friedlander, E.), Annals of Mathematical Studies, Volume 143, pp. 188–238 (Princeton University Press, 2000).Google Scholar
37.Voevodsky, V., Cancellation theorem, preprint (available at http://www.math.uiuc.edu/K-theory/0541/, 2002).Google Scholar