Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T10:42:47.389Z Has data issue: false hasContentIssue false
  • English
  • Français

DAUGAVET PROPERTY IN TENSOR PRODUCT SPACES

Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  21 November 2019

Abraham Rueda Zoca Open the ORCID record for Abraham Rueda Zoca [Opens in a new window] ,
Pedro Tradacete Open the ORCID record for Pedro Tradacete [Opens in a new window]  and
Ignacio Villanueva
Abraham Rueda Zoca
Affiliation:
Universidad de Granada, Facultad de Ciencias, Departamento de Análisis Matemático, 18071-Granada, Spain ([email protected]), URL: https://arzenglish.wordpress.com
Pedro Tradacete
Affiliation:
Instituto de Ciencias Matemáticas (CSIC-UAM-UC3M-UCM), Consejo Superior de Investigaciones Científicas, C/ Nicolás Cabrera, 13–15, Campus de Cantoblanco UAM, 28049Madrid, Spain ([email protected]), URL: https://www.icmat.es/miembros/ptradacete/
Ignacio Villanueva
Affiliation:
Universidad Complutense de Madrid, Departamento de Análisis Matemtico y Matemática Aplicada, Instituto de Matemática Interdisciplinar-IMI, Instituto de Ciencias Matemáticas ICMAT, Madrid, Spain ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the Daugavet property in tensor products of Banach spaces. We show that 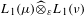$L_{1}(\unicode[STIX]{x1D707})\widehat{\otimes }_{\unicode[STIX]{x1D700}}L_{1}(\unicode[STIX]{x1D708})$ has the Daugavet property when $\unicode[STIX]{x1D707}$ and $\unicode[STIX]{x1D708}$ are purely non-atomic measures. Also, we show that 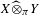$X\widehat{\otimes }_{\unicode[STIX]{x1D70B}}Y$ has the Daugavet property provided 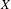$X$ and $Y$ are 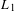$L_{1}$-preduals with the Daugavet property, in particular, spaces of continuous functions with this property. With the same techniques, we also obtain consequences about roughness in projective tensor products as well as the Daugavet property of projective symmetric tensor products.

Keywords

Daugavet propertytensor product spacesoctahedral norms

MSC classification

Primary: 46B04: Isometric theory of Banach spaces
Secondary: 46B20: Geometry and structure of normed linear spaces 46B28: Spaces of operators; tensor products; approximation properties
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 4 , July 2021 , pp. 1409 - 1428
Check for updates
Copyright
© The Author(s), 2019. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The research of the first author was supported by MECD (Spain) FPU2016/00015, MICINN (Spain) Grant PGC2018-093794-B-I00 (MCIU, AEI, FEDER, UE), Junta de Andalucía Grant A-FQM-484-UGR18 and Junta de Andalucía Grant FQM-0185. The second author gratefully acknowledges the support of MINECO (Spain) through grants MTM2016-76808-P (AEI/FEDER, UE) and MTM2016-75196-P (AEI/FEDER, UE) and the ‘Severo Ochoa Programme for Centres of Excellence in R&D’ (SEV-2015-0554). The third author was supported by MINECO (Spain) Grant MTM2017-88385-P, QUITEMAD+-CM (S2013/ICE- 2801) and the ‘Severo Ochoa Programme for Centres of Excellence in R&D’ (SEV-2015-0554).

References

Abrahansen, T. A., Lima, V. and Nygaard, O., Remarks on diameter two properties, J. Convex Anal. 20(2) (2013), 439–452.Google Scholar
Acosta, M. D., Becerra Guerrero, J. and Rodríguez-Palacios, A., Weakly open sets in the unit ball of the projective tensor product of Banach spaces, J. Math. Anal. Appl. 383 (2011), 461–473.CrossRefGoogle Scholar
Albiac, F. and Kalton, N., Topics in Banach Space Theory, Graduate Texts in Mathematics, Volume 233 (Springer, New York, 2006).Google Scholar
Avilés, A., Cabello Sánchez, F., Castillo, J. M. F., González, M. and Moreno, Y., Separably Injective Banach Spaces, Lecture Notes in Mathematics, Volume 2132 (Springer, Cham, 2016).CrossRefGoogle Scholar
Becerra Guerrero, J., López-Pérez, G. and Rueda Zoca, A., Extreme differences between weakly open subsets and convex combinations of slices in Banach spaces, Adv. Math. 269 (2015), 56–70.CrossRefGoogle Scholar
Becerra Guerrero, J., López-Pérez, G. and Rueda Zoca, A., Diametral diameter two properties in Banach spaces, J. Convex Anal. 25(3) (2018), 817–840.Google Scholar
Becerra Guerrero, J. and Martín, M., The Daugavet property of C ∗ -algebras, JB ∗ -triples and of their isometric preduals, J. Funct. Anal. 224 (2005), 316–337.CrossRefGoogle Scholar
Becerra Guerrero, J. and Martín, M., A characterisation of the Daugavet property for Lindenstrauss spaces, in Methods in Banach Space Theory (ed. Castillo, J. M. F. and Johnson, W. B.), London Mathematical Society Lecture Note Series, Volume 337, pp. 91–96 (Cambridge University Press, Cambridge, 2006).CrossRefGoogle Scholar
Becerra Guerrero, J. and Rodríguez-Palacios, A., Banach spaces with the Daugavet property, and the centralizer, J. Funct. Anal. 254 (2008), 2294–2302.CrossRefGoogle Scholar
Brach, S., Sánchez Pérez, E. and Werner, D., The Daugavet equation for bounded vector valued functions, Rocky Mountain J. Math. 47(6) (2017), 1765–1801.CrossRefGoogle Scholar
Daugavet, I. K., On a property of completely continuous operators in the space C, Uspekhi Mat. Nauk 18 (1963), 157–158. (Russian).Google Scholar
Defant, A. and Floret, K., Tensor Norms and Operator Ideals (North Holland, Amsterdam, 1993).Google Scholar
Deville, R., Godefroy, G. and Zizler, V., Smoothness and Renormings in Banach Spaces, Pitman Monographs and Surveys in Pure and Applied Mathematics, Volume 64 (Longman Scientific & Technical, Harlow, 1993).Google Scholar
Floret, K., Natural norms on symmetric tensor products of normed spaces, Note Mat. 17 (1997), 153–188.Google Scholar
Gutiérrez, J. M., Jaramillo, J. A. and Llavona, J. G., Polynomials and geometry of Banach spaces, Extracta Math. 10(2) (1995), 79–114.Google Scholar
Haller, R., Langemets, J. and Põldvere, M., On duality of diameter 2 properties, J. Convex Anal. 22(2) (2015), 465–483.Google Scholar
Ivakhno, Y., Kadets, V. and Werner, D., The Daugavet property for spaces of Lipschitz functions, Math. Scand. 101 (2007), 261–279.CrossRefGoogle Scholar
Kadets, V., Kalton, N. and Werner, D., Remarks on rich subspaces of Banach spaces, Studia Math. 159(2) (2003), 195–206.CrossRefGoogle Scholar
Kadets, V., Shepelska, V. and Werner, D., Thickness of the unit sphere, ℓ 1 -types, and the almost Daugavet property, Houston J. Math. 37(3) (2011), 867–878.Google Scholar
Kadets, V., Shvidkoy, R., Sirotkin, G. and Werner, D., Banach spaces with the Daugavet property, Trans. Amer. Math. Soc. 352(2) (2000), 855–873.CrossRefGoogle Scholar
Kadets, V. and Werner, D., A Banach space with the Schur and the Daugavet property, Proc. Amer. Math. Soc. 132(6) (2004), 1765–1773.CrossRefGoogle Scholar
Langemets, J., Geometrical Structure in Diameter 2 Banach Spaces, Dissertationes Mathematicae Universitatis Tartuensis, Volume 99 (2015). http://dspace.ut.ee/handle/10062/47446.Google Scholar
Langemets, J., Lima, V. and Rueda Zoca, A., Almost square and octahedral norms in tensor products of Banach spaces, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 111 (2017), 841–853.CrossRefGoogle Scholar
Langemets, J., Lima, V. and Rueda Zoca, A., Octahedral norms in tensor products of Banach spaces, Q. J. Math. 68(4) (2017), 1247–1260.CrossRefGoogle Scholar
Lindenstrauss, J., Extension of compact operators, Mem. Amer. Math. Soc. 48 (1964).Google Scholar
Lotz, H. P., Extensions and liftings of positive linear mappings on Banach lattices, Trans. Amer. Math. Soc. 211 (1975), 85–100.CrossRefGoogle Scholar
Meyer-Nieberg, P., Banach Lattices, Universitext, (Springer, Berlin, 1991).CrossRefGoogle Scholar
Rueda Zoca, A., Daugavet property and separability in Banach spaces, Banach J. Math. Anal. 12(1) (2018), 68–84.CrossRefGoogle Scholar
Ryan, R. A., Introduction to Tensor Products of Banach Spaces, Springer Monographs in Mathematics, (Springer, London, 2002).CrossRefGoogle Scholar
Werner, D., Recent progress on the Daugavet property, Irish Math. Soc. Bull. 46 (2001), 77–97.Google Scholar
Wojtaszczyk, P., Some remarks on the Daugavet equation, Proc. Amer. Math. Soc. 115(4) (1992), 1047–1052.CrossRefGoogle Scholar