Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T16:57:13.770Z Has data issue: false hasContentIssue false
  • English
  • Français

COSIMPLICIAL SPACES AND COCYCLES

Part of: Algebraic geometry: Foundations Homological algebra Applied homological algebra and category theory

Published online by Cambridge University Press:  10 November 2014

J. F. Jardine
J. F. Jardine*
Affiliation:
Department of Mathematics, University of Western Ontario, London, Ontario N6A 5B7, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Standard results from non-abelian cohomology theory specialize to a theory of torsors and stacks for cosimplicial groupoids. The space of global sections of the stack completion of a cosimplicial groupoid 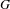$G$ is weakly equivalent to the Bousfield–Kan total complex of 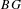$BG$ for all cosimplicial groupoids 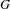$G$. The 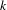$k$-invariants for the Postnikov tower of a cosimplicial space 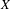$X$ are naturally elements of stack cohomology for the stack associated to the fundamental groupoid 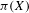${\it\pi}(X)$ of 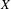$X$. Cocycle-theoretic ideas and techniques are used throughout the paper.

Keywords

cosimplicial spacesnon-abelian cohomologycocycles

MSC classification

Primary: 55U35: Abstract and axiomatic homotopy theory
Secondary: 18G50: Nonabelian homological algebra 14A20: Generalizations (algebraic spaces, stacks)
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 15 , Issue 3 , July 2016 , pp. 445 - 470
Copyright
© Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bousfield, A. K. and Kan, D. M., Homotopy Limits, Completions and Localizations, Lecture Notes in Mathematics, Volume 304 (Springer-Verlag, Berlin, 1972).Google Scholar
Goerss, P. G. and Jardine, J. F., Simplicial Homotopy Theory, Progress in Mathematics, Volume 174 (Birkhäuser Verlag, Basel, 1999).Google Scholar
Hollander, S., A homotopy theory for stacks, Israel J. Math. 163 (2008), 93–124.Google Scholar
Jardine, J. F., Simplicial objects in a Grothendieck topos, in Applications of Algebraic K-theory to Algebraic Geometry and Number Theory, Part I, II, pp. 193–239 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Jardine, J. F., Simplicial presheaves, J. Pure Appl. Algebra 47(1) (1987), 35–87.Google Scholar
Jardine, J. F., Generalized Étale Cohomology Theories, Progress in Mathematics, Volume 146 (Birkhäuser Verlag, Basel, 1997).Google Scholar
Jardine, J. F., Categorical homotopy theory, Homology, Homotopy Appl. 8(1) (2006), 71–144 (electronic).Google Scholar
Jardine, J. F., Fibred sites and stack cohomology, Math. Z. 254(4) (2006), 811–836.Google Scholar
Jardine, J. F., Cocycle categories, in Algebraic Topology, Abeel Symposia, Volume 4, pp. 185–218 (Springer, Berlin, 2009).Google Scholar
Jardine, J. F., Local Homotopy Theory, Springer Monographs in Mathematics (2015), in press, http://www.springer.com/mathematics/algebra/book/978-1-4939-2299-4.Google Scholar
Joyal, A. and Tierney, M., Strong stacks and classifying spaces, in Category Theory (Como, 1990), Lecture Notes in Math, Volume 1488, pp. 213–236 (Springer, Berlin, 1991).Google Scholar
Thomason, R. W., Algebraic K-theory and étale cohomology, Ann. Sci. Éc. Norm. Supér. (4) 18(3) (1985), 437–552.Google Scholar