No CrossRef data available.
Published online by Cambridge University Press: 10 March 2023
Motivated by some models of pattern formation involving an unoriented director field in the plane, we study a family of unoriented counterparts to the Aviles–Giga functional. We introduce a nonlinear 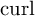 $\operatorname {\mathrm {curl}}$ operator for such unoriented vector fields as well as a family of even entropies which we call ‘trigonometric entropies’. Using these tools, we show two main theorems which parallel some results in the literature on the classical Aviles–Giga energy. The first is a compactness result for sequences of configurations with uniformly bounded energies. The second is a complete characterization of zero-states, that is, the limit configurations when the energies go to 0. These are Lipschitz continuous away from a locally finite set of points, near which they form either a vortex pattern or a disclination with degree 1/2. The proof is based on a combination of regularity theory together with techniques coming from the study of the Ginzburg–Landau energy. Our methods provide alternative proofs in the classical Aviles–Giga context.
$\operatorname {\mathrm {curl}}$ operator for such unoriented vector fields as well as a family of even entropies which we call ‘trigonometric entropies’. Using these tools, we show two main theorems which parallel some results in the literature on the classical Aviles–Giga energy. The first is a compactness result for sequences of configurations with uniformly bounded energies. The second is a complete characterization of zero-states, that is, the limit configurations when the energies go to 0. These are Lipschitz continuous away from a locally finite set of points, near which they form either a vortex pattern or a disclination with degree 1/2. The proof is based on a combination of regularity theory together with techniques coming from the study of the Ginzburg–Landau energy. Our methods provide alternative proofs in the classical Aviles–Giga context.