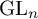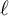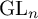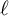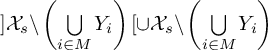1 Introduction
Soit
![]() $d\geq 1$
un entier et p un nombre premier, nous étudierons dans cet article la cohomologie de de Rham de
$d\geq 1$
un entier et p un nombre premier, nous étudierons dans cet article la cohomologie de de Rham de
![]() ${\mathbb {H}}_K^d$
l’espace de Drinfeld de dimension d sur K une extension finie de
${\mathbb {H}}_K^d$
l’espace de Drinfeld de dimension d sur K une extension finie de
![]() ${\mathbb {Q}}_p$
. C’est un ouvert de l’espace projective rigide, sur lequel agit naturellement
${\mathbb {Q}}_p$
. C’est un ouvert de l’espace projective rigide, sur lequel agit naturellement
![]() $G=\operatorname {\mathrm {GL}}_{d+1}(K)$
, tel que
$G=\operatorname {\mathrm {GL}}_{d+1}(K)$
, tel que
où
![]() ${\mathcal {H}}$
est l’ensemble des hyperplans K-rationnels de
${\mathcal {H}}$
est l’ensemble des hyperplans K-rationnels de
![]() ${\mathbb {P}}_K^d$
et
${\mathbb {P}}_K^d$
et
![]() $C=\widehat {\overline {K}}$
le complété d’une clôture algébrique de K.
$C=\widehat {\overline {K}}$
le complété d’une clôture algébrique de K.
Dans un article monumental [Reference Drinfel’d14], Drinfeld a construit une tour de revêtements finis étales G-équivariants
![]() $({\mathcal {M}}_{Dr}^n)_{n\geq 0}$
de l’espace
$({\mathcal {M}}_{Dr}^n)_{n\geq 0}$
de l’espace
![]() ${\mathcal {M}}_{Dr}^0:= {\mathbb {H}}_{\breve {K}}^d \times {\mathbb {Z}}$
(avec
${\mathcal {M}}_{Dr}^0:= {\mathbb {H}}_{\breve {K}}^d \times {\mathbb {Z}}$
(avec
![]() $\breve {K}= \widehat {K^{nr}}$
le complété de l’extension maximale non ramifiée dans
$\breve {K}= \widehat {K^{nr}}$
le complété de l’extension maximale non ramifiée dans
![]() $\overline {K}$
et
$\overline {K}$
et
![]() ${\mathbb {H}}_{\breve {K}}^d={\mathbb {H}}_K^d\otimes _K \breve {K}$
), de groupe de Galois
${\mathbb {H}}_{\breve {K}}^d={\mathbb {H}}_K^d\otimes _K \breve {K}$
), de groupe de Galois
![]() ${\mathcal {O}}_D^{*}$
avec D l’algèbre à division sur K de dimension
${\mathcal {O}}_D^{*}$
avec D l’algèbre à division sur K de dimension
![]() $(d+1)^2$
et d’invariant
$(d+1)^2$
et d’invariant
![]() $1/(d+1)$
. La cohomologie étale l-adique pour
$1/(d+1)$
. La cohomologie étale l-adique pour
![]() $l \neq p$
de cette tour fournit une réalisation géométrique de la correspondance de Langlands et de Jacquet-Langlands locales; cf. [Reference Harris23], [Reference Boyer5], [Reference Harris and Taylor24]. Pour
$l \neq p$
de cette tour fournit une réalisation géométrique de la correspondance de Langlands et de Jacquet-Langlands locales; cf. [Reference Harris23], [Reference Boyer5], [Reference Harris and Taylor24]. Pour
![]() $l=p$
,
$l=p$
,
![]() $d=1$
et
$d=1$
et
![]() $K={\mathbb {Q}}_p$
, il est montré dans [Reference Colmez, Dospinescu and Nizioł6] que la cohomologie étale p-adique de ces espaces encode aussi la correspondance de Langlands locale p-adique pour
$K={\mathbb {Q}}_p$
, il est montré dans [Reference Colmez, Dospinescu and Nizioł6] que la cohomologie étale p-adique de ces espaces encode aussi la correspondance de Langlands locale p-adique pour
![]() ${\mathrm {GL}}_2({\mathbb {Q}}_p)$
.
${\mathrm {GL}}_2({\mathbb {Q}}_p)$
.
Dans ce travail, nous nous intéressons à la cohomologie de de Rham de la tour de Drinfeld, guidés par le principe informel suivant: les résultats l-adiques établis dans [Reference Harris23], [Reference Boyer5], [Reference Harris and Taylor24] doivent avoir des analogues en cohomologie de de Rham, obtenus en oubliant simplement l’action du groupe de Weil
![]() $W_K$
de K et en changeant les coefficients. L’action de
$W_K$
de K et en changeant les coefficients. L’action de
![]() $W_K$
sur les groupes de cohomologie l-adique est très intéressante, mais elle devient invisible sur les groupes de cohomologie de de Rham, qui encodent uniquement les liens entre les représentations de G et de
$W_K$
sur les groupes de cohomologie l-adique est très intéressante, mais elle devient invisible sur les groupes de cohomologie de de Rham, qui encodent uniquement les liens entre les représentations de G et de
![]() $D^{*}$
. Ce genre de résultat a été démontré pour
$D^{*}$
. Ce genre de résultat a été démontré pour
![]() $ d=1$
dans [Reference Dospinescu and Le Bras12] (pour
$ d=1$
dans [Reference Dospinescu and Le Bras12] (pour
![]() $K={\mathbb {Q}}_p$
) et dans [Reference Colmez, Dospinescu and Nizioł6] (pour K quelconque), pour toute la tour de Drinfeld. Notre résultat principal est une preuve (purement locale) de ce principe quand
$K={\mathbb {Q}}_p$
) et dans [Reference Colmez, Dospinescu and Nizioł6] (pour K quelconque), pour toute la tour de Drinfeld. Notre résultat principal est une preuve (purement locale) de ce principe quand
![]() $n=1$
et d est quelconque, plus précisément pour la ‘partie supercuspidale’ de la cohomologie. Il s’agit d’un analogue en cohomologie de de Rham du résultat l-adique démontré par voie locale par Wang [Reference Wang32]. Nous utilisons de manière cruciale les résultats géométriques concernant
$n=1$
et d est quelconque, plus précisément pour la ‘partie supercuspidale’ de la cohomologie. Il s’agit d’un analogue en cohomologie de de Rham du résultat l-adique démontré par voie locale par Wang [Reference Wang32]. Nous utilisons de manière cruciale les résultats géométriques concernant
![]() ${\mathcal {M}}_{Dr}^1$
obtenus dans loc.cit (la situation est nettement plus compliquée pour
${\mathcal {M}}_{Dr}^1$
obtenus dans loc.cit (la situation est nettement plus compliquée pour
![]() ${\mathcal {M}}_{Dr}^n$
quand
${\mathcal {M}}_{Dr}^n$
quand
![]() $n>1$
, et il est peu probable qu’une approche purement locale puisse résoudre ce problème).
$n>1$
, et il est peu probable qu’une approche purement locale puisse résoudre ce problème).
Pour énoncer notre résultat principal, nous avons besoin de quelques préliminaires. Le groupe de Galois du revêtement
![]() ${\mathcal {M}}_{Dr}^1\to {\mathcal {M}}_{Dr}^0$
est
${\mathcal {M}}_{Dr}^1\to {\mathcal {M}}_{Dr}^0$
est
![]() ${\mathbb {F}}_{q^{d+1}}^{*}$
(avec
${\mathbb {F}}_{q^{d+1}}^{*}$
(avec
![]() ${\mathbb {F}}_q$
le corps résiduel de K), un groupe cyclique d’ordre premier à p (ce qui jouera un rôle fondamental par la suite). Soit
${\mathbb {F}}_q$
le corps résiduel de K), un groupe cyclique d’ordre premier à p (ce qui jouera un rôle fondamental par la suite). Soit
![]() $\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to C^{*}$
un caractère primitif de ce groupe (i.e., qui ne se factorise pas par la norme
$\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to C^{*}$
un caractère primitif de ce groupe (i.e., qui ne se factorise pas par la norme
![]() ${\mathbb {F}}_{q^{d+1}}^{*}\to {\mathbb {F}}_{q^{e}}^{*}$
pour tout diviseur e de
${\mathbb {F}}_{q^{d+1}}^{*}\to {\mathbb {F}}_{q^{e}}^{*}$
pour tout diviseur e de
![]() $d+1$
, différent de
$d+1$
, différent de
![]() $d+1$
). On peut associer à
$d+1$
). On peut associer à
![]() $\theta $
les objets suivants :
$\theta $
les objets suivants :
![]() $\bullet $
une représentation de Deligne-Lusztig (ou de Green)
$\bullet $
une représentation de Deligne-Lusztig (ou de Green)
![]() $\overline {\pi }_{\theta }$
du groupe
$\overline {\pi }_{\theta }$
du groupe
![]() $\mathrm { GL}_{d+1}({\mathbb {F}}_q)$
.
$\mathrm { GL}_{d+1}({\mathbb {F}}_q)$
.
![]() $\bullet $
une représentation de
$\bullet $
une représentation de
![]() $D^{*}$
$D^{*}$
![]() $\bullet $
une représentation de G
$\bullet $
une représentation de G
La notation est bien entendu inspirée par la correspondance de Jacquet-Langlands pour les représentations supercuspidales de niveau
![]() $0$
et de caractère central trivial sur
$0$
et de caractère central trivial sur
![]() $\varpi ^{{\mathbb {Z}}}$
.
$\varpi ^{{\mathbb {Z}}}$
.
Théorème A. Pour tout caractère primitif
![]() $\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to C^{*}$
il existe des isomorphismes de G-représentations
$\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to C^{*}$
il existe des isomorphismes de G-représentations
 $$ \begin{align*}\operatorname{\mathrm{Hom}}_{D^{*}}(\rho(\theta), \mathrm{H}^{i}_{\mathrm{dR},c}({\mathcal{M}}_{Dr, C}^1/ \varpi^{{\mathbb{Z}}})){\cong} \begin{cases} \operatorname{\mathrm{JL}}(\rho(\theta))^{d+1} &\text{ si } i=d \\ 0 &\text{ sinon} \end{cases}\!. \end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Hom}}_{D^{*}}(\rho(\theta), \mathrm{H}^{i}_{\mathrm{dR},c}({\mathcal{M}}_{Dr, C}^1/ \varpi^{{\mathbb{Z}}})){\cong} \begin{cases} \operatorname{\mathrm{JL}}(\rho(\theta))^{d+1} &\text{ si } i=d \\ 0 &\text{ sinon} \end{cases}\!. \end{align*} $$
Expliquons les difficultés qu’il faut surmonter pour prouver ce théorème. La principale est l’absence d’un modèle semi-stable (ou semi-stable généralisé; cf. ci-dessous) de l’espace
![]() ${\mathcal {M}}_{Dr}^1$
, alors que l’on dispose d’un tel modèle (construit par Deligne)
${\mathcal {M}}_{Dr}^1$
, alors que l’on dispose d’un tel modèle (construit par Deligne)
![]() $\widehat {{\mathcal {M}}}_{Dr}^0$
pour
$\widehat {{\mathcal {M}}}_{Dr}^0$
pour
![]() ${\mathcal {M}}_{Dr}^0$
(du côté Lubin-Tate, la situation est meilleure: Yoshida a construit [Reference Yoshida34] un modèle semi-stable généralisé du premier revêtement de l’espace de Lubin-Tate et étudié la géométrie de sa fibre spéciale). Le schéma formel
${\mathcal {M}}_{Dr}^0$
(du côté Lubin-Tate, la situation est meilleure: Yoshida a construit [Reference Yoshida34] un modèle semi-stable généralisé du premier revêtement de l’espace de Lubin-Tate et étudié la géométrie de sa fibre spéciale). Le schéma formel
![]() $\widehat {{\mathcal {M}}}_{Dr}^0$
possède une interprétation modulaire; grâce à un théorème fondamental de Drinfeld [Reference Drinfel’d14], ce modèle classifie des déformations par quasi-isogénie d’un
$\widehat {{\mathcal {M}}}_{Dr}^0$
possède une interprétation modulaire; grâce à un théorème fondamental de Drinfeld [Reference Drinfel’d14], ce modèle classifie des déformations par quasi-isogénie d’un
![]() ${\mathcal {O}}_D$
-module formel spécial de hauteur
${\mathcal {O}}_D$
-module formel spécial de hauteur
![]() $(d+1)^2$
au sens de Drinfeld. Soit
$(d+1)^2$
au sens de Drinfeld. Soit
![]() ${\mathfrak {X}}$
le
${\mathfrak {X}}$
le
![]() ${\mathcal {O}}_D$
-module formel spécial universel sur
${\mathcal {O}}_D$
-module formel spécial universel sur
![]() $\widehat {{\mathcal {M}}}_{Dr}^0$
, si
$\widehat {{\mathcal {M}}}_{Dr}^0$
, si
![]() $\Pi _D$
est une uniformisante de
$\Pi _D$
est une uniformisante de
![]() ${\mathcal {O}}_D$
, alors
${\mathcal {O}}_D$
, alors
![]() ${\mathfrak {X}}[\Pi _D]$
est un schéma formel en
${\mathfrak {X}}[\Pi _D]$
est un schéma formel en
![]() ${\mathbb {F}}_p$
-espaces vectoriels de Raynaud dont on connait une classification [Reference Raynaud29]. De plus,
${\mathbb {F}}_p$
-espaces vectoriels de Raynaud dont on connait une classification [Reference Raynaud29]. De plus,
![]() $\widehat {{\mathcal {M}}}_{Dr}^1$
est l’espace obtenu en analytifiant
$\widehat {{\mathcal {M}}}_{Dr}^1$
est l’espace obtenu en analytifiant
![]() ${\mathfrak {X}}[\Pi _D]\setminus \{0\}$
.
${\mathfrak {X}}[\Pi _D]\setminus \{0\}$
.
En utilisant les observations ci-dessus, on peut étudier certains ouverts de l’espace
![]() ${\mathcal {M}}_{Dr}^1$
, qui admettent un modèle lisse dont la fibre spéciale est isomorphe à une variété de Deligne-Lusztig (cette observation cruciale a été faite en premier par Teitelbaum [Reference Teitelbaum30] quand
${\mathcal {M}}_{Dr}^1$
, qui admettent un modèle lisse dont la fibre spéciale est isomorphe à une variété de Deligne-Lusztig (cette observation cruciale a été faite en premier par Teitelbaum [Reference Teitelbaum30] quand
![]() $d=1$
et a été généralisée par Wang [Reference Wang32]). La difficulté est alors de montrer que l’étude de ces ouverts suffit à comprendre la cohomologie de l’espace tout entier. En cohomologie l-adique, cela se fait par une étude délicate des cycles évanescents pour relier des questions sur
$d=1$
et a été généralisée par Wang [Reference Wang32]). La difficulté est alors de montrer que l’étude de ces ouverts suffit à comprendre la cohomologie de l’espace tout entier. En cohomologie l-adique, cela se fait par une étude délicate des cycles évanescents pour relier des questions sur
![]() ${\mathcal {M}}_{Dr}^1$
à des questions sur la fibre spéciale et plus particulièrement, sur la variété de Deligne-Lusztig. Ces méthodes sont propres à la cohomologie l-adique et pour surmonter cet obstacle, nous avons besoin du point technique suivant. Soit
${\mathcal {M}}_{Dr}^1$
à des questions sur la fibre spéciale et plus particulièrement, sur la variété de Deligne-Lusztig. Ces méthodes sont propres à la cohomologie l-adique et pour surmonter cet obstacle, nous avons besoin du point technique suivant. Soit
![]() ${\mathcal {X}}$
un schéma formel sur
${\mathcal {X}}$
un schéma formel sur
![]() ${\mathcal {O}}_K$
, localement de type fini. On dit que
${\mathcal {O}}_K$
, localement de type fini. On dit que
![]() ${\mathcal {X}}$
est de réduction semi-stable généralisée si Zariski-localement sur
${\mathcal {X}}$
est de réduction semi-stable généralisée si Zariski-localement sur
![]() ${\mathcal {X}}$
on peut trouver un morphisme étale vers
${\mathcal {X}}$
on peut trouver un morphisme étale vers
![]() $\mathrm {Spf}({\mathcal {O}}_K\langle X_1,...,X_n\rangle / (X_1^{\alpha _1}...X_r^{\alpha _r}-\varpi )$
pour certains
$\mathrm {Spf}({\mathcal {O}}_K\langle X_1,...,X_n\rangle / (X_1^{\alpha _1}...X_r^{\alpha _r}-\varpi )$
pour certains
![]() $r\leq n$
et
$r\leq n$
et
![]() $\alpha _i\geq 1$
(ou
$\alpha _i\geq 1$
(ou
![]() $\varpi $
est une uniformisante de K). Si l’on peut choisir les
$\varpi $
est une uniformisante de K). Si l’on peut choisir les
![]() $\alpha _i$
égaux à
$\alpha _i$
égaux à
![]() $1$
, on parle de réduction semi-stable.
$1$
, on parle de réduction semi-stable.
Théorème B. Soit
![]() ${\mathcal {X}}$
un schéma formel de réduction semi-stable généralisée,
${\mathcal {X}}$
un schéma formel de réduction semi-stable généralisée,
![]() ${\mathcal {X}}_s=\bigcup \limits _{{\substack {i\in I}}}^{}{Y_i}$
la décomposition en composantes irréductibles de la fibre spéciale et
${\mathcal {X}}_s=\bigcup \limits _{{\substack {i\in I}}}^{}{Y_i}$
la décomposition en composantes irréductibles de la fibre spéciale et
![]() $\pi : {\mathcal {T}}\rightarrow {\mathcal {X}}_\eta $
un revêtement étale en fibre générique de groupe de Galois
$\pi : {\mathcal {T}}\rightarrow {\mathcal {X}}_\eta $
un revêtement étale en fibre générique de groupe de Galois
![]() $\mu _n$
avec
$\mu _n$
avec
![]() $n\wedge p=1$
. Si
$n\wedge p=1$
. Si
![]() ${\mathcal {T}}={\mathcal {X}}_\eta $
ou bien
${\mathcal {T}}={\mathcal {X}}_\eta $
ou bien
![]() ${\mathcal {X}}$
est de réduction semi-stable et
${\mathcal {X}}$
est de réduction semi-stable et
![]() ${\mathcal {T}}$
est quelconque, alors pour toute partie finie J de I on a un isomorphisme naturel
${\mathcal {T}}$
est quelconque, alors pour toute partie finie J de I on a un isomorphisme naturel
 $$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J[_{\mathcal{X}}))\xrightarrow[]{\sim} \mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_{J}\backslash \bigcup_{i\notin J}Y_i[_{\mathcal{X}})) \end{align*}$$
$$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J[_{\mathcal{X}}))\xrightarrow[]{\sim} \mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_{J}\backslash \bigcup_{i\notin J}Y_i[_{\mathcal{X}})) \end{align*}$$
où
![]() $ Y_J=\bigcap \limits _{{\substack {j\in J}}}^{}{Y_j}$
.
$ Y_J=\bigcap \limits _{{\substack {j\in J}}}^{}{Y_j}$
.
Le cas
![]() $n=1$
et
$n=1$
et
![]() ${\mathcal {X}}$
semi-stable (non généralisé) est dû à Grosse-Klönne. On a un analogue en cohomologie étale l-adique en termes de cycles évanescents quand
${\mathcal {X}}$
semi-stable (non généralisé) est dû à Grosse-Klönne. On a un analogue en cohomologie étale l-adique en termes de cycles évanescents quand
![]() ${\mathcal {X}}$
est algébrisable et
${\mathcal {X}}$
est algébrisable et
![]() $| J | =n=1$
démontré par Zheng [Reference Zheng35] (voir aussi [Reference Dat8]). Nous aurons besoin uniquement du cas où
$| J | =n=1$
démontré par Zheng [Reference Zheng35] (voir aussi [Reference Dat8]). Nous aurons besoin uniquement du cas où
![]() ${\mathcal {X}}$
est semi-stable dans cet article (par contre il est indispensable de travailler avec J et
${\mathcal {X}}$
est semi-stable dans cet article (par contre il est indispensable de travailler avec J et
![]() ${\mathcal {T}}$
quelconques), mais le cas semi-stable généralisé devrait être utile pour l’étude du premier revêtement de l’espace de Lubin-Tate.
${\mathcal {T}}$
quelconques), mais le cas semi-stable généralisé devrait être utile pour l’étude du premier revêtement de l’espace de Lubin-Tate.
Au vu de la description de la géométrie de
![]() ${\mathcal {M}}_{Dr}^1$
et du théorème B, nous pouvons établir:
${\mathcal {M}}_{Dr}^1$
et du théorème B, nous pouvons établir:
Théorème C. Soit
![]() $\theta $
un caractère primitif de
$\theta $
un caractère primitif de
![]() ${\mathbb {F}}_{q^{d+1}}^{*}$
et notons
${\mathbb {F}}_{q^{d+1}}^{*}$
et notons
![]() ${\mathcal {B}}{\mathcal {T}}_0$
l’ensemble des sommets de l’immeuble de Bruhat-Tits semi-simple de G. On a des isomorphismes
${\mathcal {B}}{\mathcal {T}}_0$
l’ensemble des sommets de l’immeuble de Bruhat-Tits semi-simple de G. On a des isomorphismes
où
![]() $\operatorname {\mathrm {DL}}_{{\mathbb {F}}_q}$
est la variété de Deligne-Lusztig introduite dans 4.1.
$\operatorname {\mathrm {DL}}_{{\mathbb {F}}_q}$
est la variété de Deligne-Lusztig introduite dans 4.1.
Le théorème principal A découlera alors de la théorie de Deligne-Lusztig que nous rappelons dans la partie 4.2.
Toutefois, pour étudier les intersections quelconques de tubes au dessus de composantes
![]() $\pi ^{-1}(] Y_J [)$
, nous aurons besoin de façon essentielle de la description globale du torseur
$\pi ^{-1}(] Y_J [)$
, nous aurons besoin de façon essentielle de la description globale du torseur
![]() $\Sigma ^1 \to {\mathbb {H}}^d_K$
réalisé dans [Reference Junger27] que l’on restreindra à
$\Sigma ^1 \to {\mathbb {H}}^d_K$
réalisé dans [Reference Junger27] que l’on restreindra à
![]() $\pi ^{-1}(] Y_J [) \to ] Y_J [$
.
$\pi ^{-1}(] Y_J [) \to ] Y_J [$
.
Remerciements
Le présent travail a été, avec [Reference Junger25, Reference Junger27, Reference Junger26], en grande partie réalisé durant ma thèse à l’ENS de Lyon, et a pu bénéficier des nombreux conseils et de l’accompagnement constant de mes deux maîtres de thèse Vincent Pilloni et Gabriel Dospinescu. Je les en remercie très chaleureusement. La preuve du résultat 5.8 doit beaucoup aux conseils de Laurent Fargues (pour m’avoir suggéré de voir le complexe de de Rham sur un revêtement comme une somme directe de complexe sur la base suivant les parties isotypiques) et de Jean-Claude Sikorav (pour l’explication du cas analogue sur le corps des complexes).
2 Préliminaires
2.1 Conventions générales
On fixe dans tout l’article un nombre premier p et une extension finie K de
![]() ${\mathbb {Q}}_p$
, dont on note
${\mathbb {Q}}_p$
, dont on note
![]() $\mathcal {O}_K$
l’anneau des entiers,
$\mathcal {O}_K$
l’anneau des entiers,
![]() $\varpi $
une uniformisante et
$\varpi $
une uniformisante et
![]() ${\mathbb {F}}={\mathbb {F}}_q$
le corps résiduel. On note
${\mathbb {F}}={\mathbb {F}}_q$
le corps résiduel. On note
![]() $C=\hat {\overline {K}}$
le complété d’une clôture algébrique de K et
$C=\hat {\overline {K}}$
le complété d’une clôture algébrique de K et
![]() $\breve {K}$
le complété de l’extension maximale non ramifiée de K. Soit
$\breve {K}$
le complété de l’extension maximale non ramifiée de K. Soit
![]() $L\subset C$
une extension complète de K, susceptible de varier, d’anneau des entiers
$L\subset C$
une extension complète de K, susceptible de varier, d’anneau des entiers
![]() $\mathcal {O}_L$
, d’idéal maximal
$\mathcal {O}_L$
, d’idéal maximal
![]() ${\mathfrak {m}}_L$
et de corps résiduel
${\mathfrak {m}}_L$
et de corps résiduel
![]() $\kappa $
.
$\kappa $
.
Si S est un L-espace analytique, on note
![]() ${\mathbb {A}}^n_{ S}$
(resp.
${\mathbb {A}}^n_{ S}$
(resp.
![]() ${\mathbb {P}}_{ S}^n$
) l’espace analytique affine (resp. projectif) sur S, de dimension relative n. Les espaces
${\mathbb {P}}_{ S}^n$
) l’espace analytique affine (resp. projectif) sur S, de dimension relative n. Les espaces
![]() $\mathring {{\mathbb {B}}}^n_S$
et
$\mathring {{\mathbb {B}}}^n_S$
et
![]() ${\mathbb {B}}^n_S$
seront les boules unitées ouverte et fermée.
${\mathbb {B}}^n_S$
seront les boules unitées ouverte et fermée.
Si X est un L-espace analytique et si
![]() $F\subset \mathcal {O}(X)$
est une famille finie de fonctions analytiques sur X et g une autre fonction analytique, on note
$F\subset \mathcal {O}(X)$
est une famille finie de fonctions analytiques sur X et g une autre fonction analytique, on note
 $$ \begin{align*}X\left(\frac{F}{g}\right)=\left\lbrace x\in X|\,\forall f\in F, |f(x)|\leq |g(x)|\right\rbrace, \,\, X\left(\frac{g}{F}\right)=\left\lbrace x\in X|\,\forall f\in F, |g(x)|\leq |f(x)|\right\rbrace.\end{align*} $$
$$ \begin{align*}X\left(\frac{F}{g}\right)=\left\lbrace x\in X|\,\forall f\in F, |f(x)|\leq |g(x)|\right\rbrace, \,\, X\left(\frac{g}{F}\right)=\left\lbrace x\in X|\,\forall f\in F, |g(x)|\leq |f(x)|\right\rbrace.\end{align*} $$
De même,
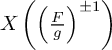 $X\left (\left (\frac {F}{g}\right )^{\pm 1}\right )$
ou
$X\left (\left (\frac {F}{g}\right )^{\pm 1}\right )$
ou
![]() $X\left (\frac {F}{g},\frac {g}{F}\right )$
désignera
$X\left (\frac {F}{g},\frac {g}{F}\right )$
désignera
![]() $\left \lbrace x\in X|\, \forall f\in F, |f(x)|= |g(x)|\right \rbrace $
. Pour
$\left \lbrace x\in X|\, \forall f\in F, |f(x)|= |g(x)|\right \rbrace $
. Pour
![]() $s\in |C^{*}|$
on note
$s\in |C^{*}|$
on note
![]() $X\left (\frac {F}{s}\right )=\left \lbrace x\in X|\, \forall f\in F, |f(x)|\leq s\right \rbrace $
(idem pour
$X\left (\frac {F}{s}\right )=\left \lbrace x\in X|\, \forall f\in F, |f(x)|\leq s\right \rbrace $
(idem pour
![]() $X\left (\frac {s}{F}\right )$
).
$X\left (\frac {s}{F}\right )$
).
Les éléments de la base canonique de
![]() ${\mathbb {Z}}^n$
seront notés
${\mathbb {Z}}^n$
seront notés
![]() $(\delta _i)_i$
. Si
$(\delta _i)_i$
. Si
![]() $x=(x_1,\cdots ,x_n)$
,
$x=(x_1,\cdots ,x_n)$
,
![]() $\alpha \in {\mathbb {Z}}^n$
et
$\alpha \in {\mathbb {Z}}^n$
et
![]() $A\in \operatorname {\mathrm {M}}_{k,n} ({\mathbb {Z}})$
, nous adopterons la notation multi-indice (i.e.,
$A\in \operatorname {\mathrm {M}}_{k,n} ({\mathbb {Z}})$
, nous adopterons la notation multi-indice (i.e.,
![]() $x^\alpha =\prod \limits _{{\substack {i=1}}}^{n}{x_i^{\alpha _i}}$
et
$x^\alpha =\prod \limits _{{\substack {i=1}}}^{n}{x_i^{\alpha _i}}$
et
![]() $x^A=(x^{A\delta _i})_{1\leq i\leq k}$
).
$x^A=(x^{A\delta _i})_{1\leq i\leq k}$
).
2.2 Cohomologie étale et torseurs
Soit n premier à p, on identifie
![]() $\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X, \mu _n)$
et l’ensemble des classes d’isomorphisme de
$\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X, \mu _n)$
et l’ensemble des classes d’isomorphisme de
![]() $\mu _n$
-torseurs sur X (i.e., des revêtements galoisiens
$\mu _n$
-torseurs sur X (i.e., des revêtements galoisiens
![]() $\pi : {\mathcal {T}} \to X$
de groupe de Galois
$\pi : {\mathcal {T}} \to X$
de groupe de Galois
![]() $\mu _n$
). On note
$\mu _n$
). On note
![]() $ [{\mathcal {T}}]$
la classe d’isomorphisme du torseur
$ [{\mathcal {T}}]$
la classe d’isomorphisme du torseur
![]() ${\mathcal {T}}$
, vue comme un élément de
${\mathcal {T}}$
, vue comme un élément de
![]() $\mathrm { H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X, \mu _n)$
. Si
$\mathrm { H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X, \mu _n)$
. Si
![]() ${\mathcal {T}}_1,{\mathcal {T}}_2$
sont des
${\mathcal {T}}_1,{\mathcal {T}}_2$
sont des
![]() $\mu _n$
-torseurs sur X, alors
$\mu _n$
-torseurs sur X, alors
![]() ${\mathcal {T}}_1 \times _X {\mathcal {T}}_2 \to X$
est un revêtement de groupe de Galois
${\mathcal {T}}_1 \times _X {\mathcal {T}}_2 \to X$
est un revêtement de groupe de Galois
![]() $\mu _n^2$
et en notant
$\mu _n^2$
et en notant
![]() $H\cong\mu_n$
l’antidiagonal, le quotient
$H\cong\mu_n$
l’antidiagonal, le quotient
![]() ${\mathcal {T}}_3={\mathcal {T}}_1\times _X {\mathcal {T}}_2 /H$
est un revêtement de X de groupe de Galois
${\mathcal {T}}_3={\mathcal {T}}_1\times _X {\mathcal {T}}_2 /H$
est un revêtement de X de groupe de Galois
![]() $\mu_n^2/H\cong\mu_n$
et
$\mu_n^2/H\cong\mu_n$
et
![]() $[{\mathcal {T}}_1]+[{\mathcal {T}}_2]= [{\mathcal {T}}_3]$
. Il est à remarquer que
$[{\mathcal {T}}_1]+[{\mathcal {T}}_2]= [{\mathcal {T}}_3]$
. Il est à remarquer que
![]() ${\mathcal {T}}_1\times _X {\mathcal {T}}_2$
est encore un revêtement de
${\mathcal {T}}_1\times _X {\mathcal {T}}_2$
est encore un revêtement de
![]() ${\mathcal {T}}_3$
de groupe de Galois
${\mathcal {T}}_3$
de groupe de Galois
![]() $H\cong\mu_n$
.
$H\cong\mu_n$
.
Le morphisme de Kummer sera noté
![]() $\kappa : {\mathscr {O}}^{*} (X)\to \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X,\mu _n)$
. Le torseur
$\kappa : {\mathscr {O}}^{*} (X)\to \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X,\mu _n)$
. Le torseur
![]() $\kappa (u)$
associé à une fonction inversible u sur X sera noté
$\kappa (u)$
associé à une fonction inversible u sur X sera noté
![]() $\pi : X(u^{1/n}) \to X$
. Si
$\pi : X(u^{1/n}) \to X$
. Si
![]() $U\subset X$
est un ouvert affinoïde, alors
$U\subset X$
est un ouvert affinoïde, alors
2.3 Cohomologie de de Rham et torseurs
Si X est un affinoïde sur L, on notera
![]() $X^\dagger $
l’espace surconvergent associé. Si
$X^\dagger $
l’espace surconvergent associé. Si
![]() $X^\dagger $
est un espace surconvergent lisse, d’espace rigide analytique sous-jacent X, on note
$X^\dagger $
est un espace surconvergent lisse, d’espace rigide analytique sous-jacent X, on note
![]() $\mathrm {H}^{*}_{\mathrm {dR}}(X)$
et
$\mathrm {H}^{*}_{\mathrm {dR}}(X)$
et
![]() $\mathrm {H}^{*}_{\mathrm {dR}}(X^\dagger )$
les hypercohomologies des complexes de de Rham
$\mathrm {H}^{*}_{\mathrm {dR}}(X^\dagger )$
les hypercohomologies des complexes de de Rham
![]() $\Omega _{X/L}^\bullet $
et
$\Omega _{X/L}^\bullet $
et
![]() $\Omega _{X^\dagger /L}^\bullet $
. Par [Reference Grosse-Klönne19, Proposition 2.5], le théorème B de Kiehl [Reference Kiehl28, Satz 2.4.2] et la suite spectrale de Hodge-de Rham, ces cohomologies sont calculées directement à partir du complexe de de Rham correspondant, quand X est Stein.Footnote
1
Les deux cohomologies coïncident si X est partiellement propre (par exemple Stein).
$\Omega _{X^\dagger /L}^\bullet $
. Par [Reference Grosse-Klönne19, Proposition 2.5], le théorème B de Kiehl [Reference Kiehl28, Satz 2.4.2] et la suite spectrale de Hodge-de Rham, ces cohomologies sont calculées directement à partir du complexe de de Rham correspondant, quand X est Stein.Footnote
1
Les deux cohomologies coïncident si X est partiellement propre (par exemple Stein).
Soit n premier à p et
![]() $\pi :{\mathcal {T}} \to X$
un
$\pi :{\mathcal {T}} \to X$
un
![]() $\mu _n$
-torseur d’un espace analytique lisse X. On a une décomposition
$\mu _n$
-torseur d’un espace analytique lisse X. On a une décomposition
![]() $\pi _* {\mathscr {O}}_{{\mathcal {T}}} = \bigoplus \limits _{{\substack {\chi \in \mu _n^{\lor }}}}^{}{{\mathscr {L}}_{\chi }}$
où
$\pi _* {\mathscr {O}}_{{\mathcal {T}}} = \bigoplus \limits _{{\substack {\chi \in \mu _n^{\lor }}}}^{}{{\mathscr {L}}_{\chi }}$
où
![]() ${\mathscr {L}}_\chi $
est l’espace propre associé au caractère
${\mathscr {L}}_\chi $
est l’espace propre associé au caractère
![]() $\chi $
pour l’action de
$\chi $
pour l’action de
![]() $\mu _n$
(c’est un faisceau localement libre de rang 1). Le morphisme
$\mu _n$
(c’est un faisceau localement libre de rang 1). Le morphisme
![]() $\pi $
étant étale, on a
$\pi $
étant étale, on a
 $$ \begin{align*}\pi_* \Omega_{{\mathcal{T}} /L}^q=\Omega_{X/L}^q\otimes \pi_* {\mathscr{O}}_{{\mathcal{T}}}=\bigoplus\limits_{{\substack{\chi \in \mu_n^{\lor}}}}^{}{\Omega_{X/L}^q\otimes{\mathscr{L}}_{\chi}}\end{align*} $$
$$ \begin{align*}\pi_* \Omega_{{\mathcal{T}} /L}^q=\Omega_{X/L}^q\otimes \pi_* {\mathscr{O}}_{{\mathcal{T}}}=\bigoplus\limits_{{\substack{\chi \in \mu_n^{\lor}}}}^{}{\Omega_{X/L}^q\otimes{\mathscr{L}}_{\chi}}\end{align*} $$
et de même pour le complexe surconvergent. Les différentielles des complexes de de Rham étant
![]() $\mu _n$
-équivariantes, elles respectent ces décompositions en somme directe donnant lieu pour chaque
$\mu _n$
-équivariantes, elles respectent ces décompositions en somme directe donnant lieu pour chaque
![]() $\chi $
à des complexes de cochaînes
$\chi $
à des complexes de cochaînes
![]() $\Omega _{X/L}^\bullet \otimes {\mathscr {L}}_{\chi }=:\Omega _{{\mathcal {T}}/L}^\bullet [\chi ]$
et
$\Omega _{X/L}^\bullet \otimes {\mathscr {L}}_{\chi }=:\Omega _{{\mathcal {T}}/L}^\bullet [\chi ]$
et
![]() $\Omega _{X^\dagger /L}^\bullet \otimes {\mathscr {L}}_{\chi }=:\Omega _{{\mathcal {T}}^\dagger /L}^\bullet [\chi ]$
dont les cohomologies seront notées
$\Omega _{X^\dagger /L}^\bullet \otimes {\mathscr {L}}_{\chi }=:\Omega _{{\mathcal {T}}^\dagger /L}^\bullet [\chi ]$
dont les cohomologies seront notées
![]() $\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}})[\chi ]$
et
$\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}})[\chi ]$
et
![]() $\mathrm {H}^{*}_{\mathrm { dR}}({\mathcal {T}}^\dagger )[\chi ]$
. C’est la partie isotypique associée à
$\mathrm {H}^{*}_{\mathrm { dR}}({\mathcal {T}}^\dagger )[\chi ]$
. C’est la partie isotypique associée à
![]() $\chi $
. En particulier,
$\chi $
. En particulier,
Soit
![]() ${\mathcal {T}}_1\to X$
,
${\mathcal {T}}_1\to X$
,
![]() ${\mathcal {T}}_2\to Y$
deux
${\mathcal {T}}_2\to Y$
deux
![]() $\mu _n$
-torseurs sur des L-espaces lisses X et Y. On obtient
$\mu _n$
-torseurs sur des L-espaces lisses X et Y. On obtient
![]() ${\mathcal {T}}_1\times _L Y$
,
${\mathcal {T}}_1\times _L Y$
,
![]() $X\times _L {\mathcal {T}}_2$
deux revêtements sur
$X\times _L {\mathcal {T}}_2$
deux revêtements sur
![]() $X\times _L Y$
et on construit (voir plus haut pour la définition de H)
$X\times _L Y$
et on construit (voir plus haut pour la définition de H)
C’est un revêtement de
![]() $X\times _L Y$
dont la classe s’identifie à
$X\times _L Y$
dont la classe s’identifie à
![]() $[{\mathcal {T}}_1\times _L Y]+[X\times {\mathcal {T}}_2]$
. Comme
$[{\mathcal {T}}_1\times _L Y]+[X\times {\mathcal {T}}_2]$
. Comme
![]() ${\mathcal {T}}_1\times _L {\mathcal {T}}_2$
est un revêtement de
${\mathcal {T}}_1\times _L {\mathcal {T}}_2$
est un revêtement de
![]() ${\mathcal {T}}_3$
étale de groupe de Galois H, on a
${\mathcal {T}}_3$
étale de groupe de Galois H, on a
Proposition 2.1. On a des isomorphismes naturels
 $$\begin{align*}\mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}_3)=\mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}_1\times_L {\mathcal{T}}_2)^H=\bigoplus\limits_{{\substack{ q_1 +q_2=q}}}^{}{\bigoplus\limits_{{\substack{\chi\in \mu_n^\lor }}}^{}{\mathrm{H}^{q_1}_{\mathrm{dR}} ({\mathcal{T}}_1)[ \chi]\otimes \mathrm{H}^{q_2}_{\mathrm{dR}} ({\mathcal{T}}_2)[ \chi] }} , \end{align*}$$
$$\begin{align*}\mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}_3)=\mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}_1\times_L {\mathcal{T}}_2)^H=\bigoplus\limits_{{\substack{ q_1 +q_2=q}}}^{}{\bigoplus\limits_{{\substack{\chi\in \mu_n^\lor }}}^{}{\mathrm{H}^{q_1}_{\mathrm{dR}} ({\mathcal{T}}_1)[ \chi]\otimes \mathrm{H}^{q_2}_{\mathrm{dR}} ({\mathcal{T}}_2)[ \chi] }} , \end{align*}$$
idem pour la cohomologie de de Rham surconvergente.
2.4 Cohomologie rigide
La cohomologie rigide d’un schéma algébrique Y sur le corps résiduel
![]() $\kappa $
de L sera notée
$\kappa $
de L sera notée
![]() $\mathrm { H}^{*}_{\mathrm {rig}} (Y/L)$
. On rappelle la dualité de Poincaré :
$\mathrm { H}^{*}_{\mathrm {rig}} (Y/L)$
. On rappelle la dualité de Poincaré :
Proposition 2.2.
-
1. Si X est un L-affinoïde lisse, pur de dimension d, alors
 $$\begin{align*}\mathrm{H}^{i}_{\mathrm{dR}} (X^\dagger)\cong \mathrm{H}^{2d-i}_{\mathrm{dR},c} (X^\dagger)^\lor \text{ et } \mathrm{H}^{i}_{\mathrm{dR},c} (X^\dagger)\cong \mathrm{H}^{2d-i}_{\mathrm{dR}} (X^\dagger)^\lor.\end{align*}$$
$$\begin{align*}\mathrm{H}^{i}_{\mathrm{dR}} (X^\dagger)\cong \mathrm{H}^{2d-i}_{\mathrm{dR},c} (X^\dagger)^\lor \text{ et } \mathrm{H}^{i}_{\mathrm{dR},c} (X^\dagger)\cong \mathrm{H}^{2d-i}_{\mathrm{dR}} (X^\dagger)^\lor.\end{align*}$$
-
2. Si X est un L-espace lisse et Stein, pur de dimension d, alors
 $$\begin{align*}\mathrm{H}^{i}_{\mathrm{dR}} (X)\cong \mathrm{H}^{2d-i}_{\mathrm{dR},c} (X)^\lor \text{ et } \mathrm{H}^{i}_{\mathrm{dR},c} (X)\cong \mathrm{H}^{2d-i}_{\mathrm{dR}} (X)^\lor.\end{align*}$$
$$\begin{align*}\mathrm{H}^{i}_{\mathrm{dR}} (X)\cong \mathrm{H}^{2d-i}_{\mathrm{dR},c} (X)^\lor \text{ et } \mathrm{H}^{i}_{\mathrm{dR},c} (X)\cong \mathrm{H}^{2d-i}_{\mathrm{dR}} (X)^\lor.\end{align*}$$
-
3. Si Y est un schéma lisse sur
 $\kappa $
, pur de dimension d, alors
$\kappa $
, pur de dimension d, alors  $$\begin{align*}\mathrm{H}^{i}_{\mathrm{rig}} (Y/L)\cong \mathrm{H}^{2d-i}_{\mathrm{rig},c} (Y/L)^\lor \text{ et } \mathrm{H}^{i}_{\mathrm{rig},c} (Y/L)\cong \mathrm{H}^{2d-i}_{\mathrm{rig}} (Y/L)^\lor.\end{align*}$$
$$\begin{align*}\mathrm{H}^{i}_{\mathrm{rig}} (Y/L)\cong \mathrm{H}^{2d-i}_{\mathrm{rig},c} (Y/L)^\lor \text{ et } \mathrm{H}^{i}_{\mathrm{rig},c} (Y/L)\cong \mathrm{H}^{2d-i}_{\mathrm{rig}} (Y/L)^\lor.\end{align*}$$
Démonstration. Voir [Reference Grosse-Klönne19, proposition 4.9] pour le premier point, [Reference Grosse-Klönne19, proposition 4.11] pour le second et [Reference Berthelot3, théorème 2.4] pour le dernier.
Le théorème de comparaison suivant nous sera très utile:
Théorème 2.3. Soit
![]() ${\mathcal {X}}$
un schéma formel lisse sur
${\mathcal {X}}$
un schéma formel lisse sur
![]() $\operatorname {\mathrm {Spf}} ({\mathcal {O}}_L)$
, de fibre spéciale
$\operatorname {\mathrm {Spf}} ({\mathcal {O}}_L)$
, de fibre spéciale
![]() ${\mathcal {X}}_s$
et de fibre générique
${\mathcal {X}}_s$
et de fibre générique
![]() ${\mathcal {X}}_\eta $
, on a un isomorphisme naturel
${\mathcal {X}}_\eta $
, on a un isomorphisme naturel
Démonstration. Il s’agit de [Reference Grosse-Klönne21, proposition 3.6].
3 Rappels sur la géométrie de l’espace de Drinfeld
Nous rappelons quelques résultats standards concernant la géométrie de l’espace symétrique de Drinfeld et nous renvoyons à ([Reference Boutot and Carayol4, section 1, 10, sous-sections I.1. et II.6.], [Reference Dat7, sous-section 3.1.], [Reference Wang32, sous-sections 2.1. et 2.2]) pour plus de détails. On fixe une extension finie K de
![]() ${\mathbb {Q}}_p$
, une uniformisante
${\mathbb {Q}}_p$
, une uniformisante
![]() $\varpi $
de K et un entier
$\varpi $
de K et un entier
![]() $d\geq 1$
. On note
$d\geq 1$
. On note
![]() ${\mathbb {F}}={\mathbb {F}}_q$
le corps résiduel de K et
${\mathbb {F}}={\mathbb {F}}_q$
le corps résiduel de K et
![]() $G=\mathrm {GL}_{d+1}(K)$
.
$G=\mathrm {GL}_{d+1}(K)$
.
3.1 L’immeuble de Bruhat-Tits
Notons
![]() ${\mathcal {B}}{\mathcal {T}}$
l’immeuble de Bruhat-Tits associé au groupe
${\mathcal {B}}{\mathcal {T}}$
l’immeuble de Bruhat-Tits associé au groupe
![]() $\operatorname {\mathrm {PGL}}_{d+1}(K)$
. Le
$\operatorname {\mathrm {PGL}}_{d+1}(K)$
. Le
![]() $0$
-squelette
$0$
-squelette
![]() ${\mathcal {B}}{\mathcal {T}}_0$
de l’immeuble est l’ensemble des réseaux de
${\mathcal {B}}{\mathcal {T}}_0$
de l’immeuble est l’ensemble des réseaux de
![]() $K^{d+1}$
à homothétie près (i.e.,
$K^{d+1}$
à homothétie près (i.e.,
![]() ${\mathcal {B}}{\mathcal {T}}_0$
s’identifie à
${\mathcal {B}}{\mathcal {T}}_0$
s’identifie à
![]() $G/K^{*}\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)$
). Un
$G/K^{*}\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)$
). Un
![]() $(k+1)$
-uplet de sommets
$(k+1)$
-uplet de sommets
![]() $\sigma =\{s_0,\cdots , s_k\}\subset {\mathcal {B}}{\mathcal {T}}_{0} $
est un k-simplexe de
$\sigma =\{s_0,\cdots , s_k\}\subset {\mathcal {B}}{\mathcal {T}}_{0} $
est un k-simplexe de
![]() ${\mathcal {B}}{\mathcal {T}}_k$
si et seulement si, quitte à permuter les sommets
${\mathcal {B}}{\mathcal {T}}_k$
si et seulement si, quitte à permuter les sommets
![]() $s_i$
, on peut trouver pour tout i des réseaux
$s_i$
, on peut trouver pour tout i des réseaux
![]() $M_i$
avec
$M_i$
avec
![]() $s_i=[M_i]$
tels que
$s_i=[M_i]$
tels que
En posant
on obtient un drapeau
![]() $0\subsetneq \overline {M}_0\subsetneq \overline {M}_1\subsetneq \cdots \subsetneq \overline {M}_k\cong {\mathbb {F}}^{d+1}$
. On note
$0\subsetneq \overline {M}_0\subsetneq \overline {M}_1\subsetneq \cdots \subsetneq \overline {M}_k\cong {\mathbb {F}}^{d+1}$
. On note
![]() $d_i=\mathrm {dim}_{{\mathbb {F}}} (\overline {M}_i)-1$
et
$d_i=\mathrm {dim}_{{\mathbb {F}}} (\overline {M}_i)-1$
et
![]() $e_i=d_{i}-d_{i-1}.$
Nous dirons que le simplexe
$e_i=d_{i}-d_{i-1}.$
Nous dirons que le simplexe
![]() $\sigma $
est de type
$\sigma $
est de type
![]() $(e_0, e_1,\cdots , e_k)$
.
$(e_0, e_1,\cdots , e_k)$
.
Considérons une base
![]() $(\overline {f}_0,\cdots , \overline {f}_d)$
adaptée au drapeau (i.e., telle que
$(\overline {f}_0,\cdots , \overline {f}_d)$
adaptée au drapeau (i.e., telle que
![]() $\overline {M}_i=\left \langle \overline {f}_0,\cdots , \overline {f}_{d_i}\right \rangle $
pour tout i). Pour tout choix de relevés
$\overline {M}_i=\left \langle \overline {f}_0,\cdots , \overline {f}_{d_i}\right \rangle $
pour tout i). Pour tout choix de relevés
![]() $(f_0,\cdots ,f_d)$
de
$(f_0,\cdots ,f_d)$
de
![]() $(\overline {f}_0,\cdots ,\overline {f}_d)$
dans
$(\overline {f}_0,\cdots ,\overline {f}_d)$
dans
![]() $M_0$
, on a
$M_0$
, on a
où
avec
![]() $d_{-1}=-1$
. Si
$d_{-1}=-1$
. Si
![]() $(f_0,\cdots ,f_d)$
est la base canonique de
$(f_0,\cdots ,f_d)$
est la base canonique de
![]() $K^{d+1}$
, nous dirons que
$K^{d+1}$
, nous dirons que
![]() $ \sigma $
est le simplexe standard de type
$ \sigma $
est le simplexe standard de type
![]() $(e_0, e_1,\cdots , e_k)$
.
$(e_0, e_1,\cdots , e_k)$
.
La réalisation topologique de l’immeuble sera notée
![]() $|{\mathcal {B}}{\mathcal {T}}|$
. Nous confondrons les simplexes avec leur réalisation topologique de telle manière que
$|{\mathcal {B}}{\mathcal {T}}|$
. Nous confondrons les simplexes avec leur réalisation topologique de telle manière que
![]() $|{\mathcal {B}}{\mathcal {T}}|=\bigcup \limits _{{\substack {\sigma \in {\mathcal {B}}{\mathcal {T}}}}}^{}{\sigma }$
. Les différents k-simplexes, vus comme des compacts de la réalisation topologique, seront appelés faces. L’intérieur d’une face
$|{\mathcal {B}}{\mathcal {T}}|=\bigcup \limits _{{\substack {\sigma \in {\mathcal {B}}{\mathcal {T}}}}}^{}{\sigma }$
. Les différents k-simplexes, vus comme des compacts de la réalisation topologique, seront appelés faces. L’intérieur d’une face
![]() $\sigma $
sera noté
$\sigma $
sera noté
![]() $\mathring {\sigma }=\sigma \backslash \bigcup \limits _{{\substack {\sigma '\subsetneq \sigma }}}^{}{\sigma '}$
et sera appelé cellule.
$\mathring {\sigma }=\sigma \backslash \bigcup \limits _{{\substack {\sigma '\subsetneq \sigma }}}^{}{\sigma '}$
et sera appelé cellule.
3.2 L’espace des hyperplans K-rationnels
On note
![]() ${\mathcal {H}}$
l’ensemble des hyperplans K-rationnels dans
${\mathcal {H}}$
l’ensemble des hyperplans K-rationnels dans
![]() ${\mathbb {P}}^d$
. Si
${\mathbb {P}}^d$
. Si
![]() $a=(a_0,\dots , a_d)\in C^{d+1}\backslash \{0\}$
,
$a=(a_0,\dots , a_d)\in C^{d+1}\backslash \{0\}$
,
![]() $l_a$
désignera l’application
$l_a$
désignera l’application
Ainsi
![]() ${\mathcal {H}}$
s’identifie à
${\mathcal {H}}$
s’identifie à
![]() $\{\ker (l_a),\; a\in K^{d+1}\backslash \{0\} \}$
et à
$\{\ker (l_a),\; a\in K^{d+1}\backslash \{0\} \}$
et à
![]() ${\mathbb {P}}^d (K)$
.
${\mathbb {P}}^d (K)$
.
Le vecteur
![]() $a=(a_i)_{i}\in C^{d+1}$
est dit unimodulaire si
$a=(a_i)_{i}\in C^{d+1}$
est dit unimodulaire si
![]() $|a|_{\infty }(:=\max (|a_i|))=1$
. L’application
$|a|_{\infty }(:=\max (|a_i|))=1$
. L’application
![]() $a\mapsto H_a:=\ker (l_a)$
induit une bijection entre le quotient de l’ensemble des vecteurs unimodulaires
$a\mapsto H_a:=\ker (l_a)$
induit une bijection entre le quotient de l’ensemble des vecteurs unimodulaires
![]() $a\in K^{d+1}$
par l’action évidente de
$a\in K^{d+1}$
par l’action évidente de
![]() ${\mathcal {O}}_K^{*}$
et l’ensemble
${\mathcal {O}}_K^{*}$
et l’ensemble
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Pour
![]() $a\in K^{d+1}$
unimodulaire et
$a\in K^{d+1}$
unimodulaire et
![]() $n\geq 1$
, on considère l’application
$n\geq 1$
, on considère l’application
![]() $l_a^{(n)} $
$l_a^{(n)} $
et on note
Alors
![]() ${\mathcal {H}} = \varprojlim _n {\mathcal {H}}_n$
et chaque
${\mathcal {H}} = \varprojlim _n {\mathcal {H}}_n$
et chaque
![]() ${\mathcal {H}}_n$
est fini.
${\mathcal {H}}_n$
est fini.
3.3 Géométrie de l’espace symétrique de Drinfeld
Nous allons maintenant décrire l’espace symétrique de Drinfeld
![]() ${\mathbb {H}}_K^d$
. Il s’agit de l’espace analytique sur K dont les C-points sont
${\mathbb {H}}_K^d$
. Il s’agit de l’espace analytique sur K dont les C-points sont
On dispose d’une application G-équivariante
donnée par
 $$ \begin{align*}\tau (z): v\mapsto |\sum\limits_{{\substack{i=0}}}^{d}{z_i v_i}|\end{align*} $$
$$ \begin{align*}\tau (z): v\mapsto |\sum\limits_{{\substack{i=0}}}^{d}{z_i v_i}|\end{align*} $$
si
![]() $z=[z_0,\cdots , z_d] \in {\mathbb {H}}_K^d (C)$
. L’image
$z=[z_0,\cdots , z_d] \in {\mathbb {H}}_K^d (C)$
. L’image
![]() $\tau (z)$
ne dépend pas du représentant de z car les normes sont vues à homothétie près. Le fait de prendre le complémentaire des hyperplans K-rationnels assure que
$\tau (z)$
ne dépend pas du représentant de z car les normes sont vues à homothétie près. Le fait de prendre le complémentaire des hyperplans K-rationnels assure que
![]() $\tau (z)$
est séparée et donc une norme sur
$\tau (z)$
est séparée et donc une norme sur
![]() $K^{d+1}$
. D’après un résultat classique de Iwahori-Goldmann [Reference Goldman and Iwahori18], l’espace des normes sur
$K^{d+1}$
. D’après un résultat classique de Iwahori-Goldmann [Reference Goldman and Iwahori18], l’espace des normes sur
![]() $K^{d+1}$
à homothétie près s’identifie bijectivement (et de manière G-équivariante) à l’espace topologique
$K^{d+1}$
à homothétie près s’identifie bijectivement (et de manière G-équivariante) à l’espace topologique
![]() $|{\mathcal {B}}{\mathcal {T}}|$
, ce qui permet de voir
$|{\mathcal {B}}{\mathcal {T}}|$
, ce qui permet de voir
![]() $\tau $
comme une application
$\tau $
comme une application
Nous renvoyons à [Reference Boutot and Carayol4, §I.4] quand
![]() $d=1$
ou [Reference Wang32, §2.1] pour la justification des faits suivants. Soit
$d=1$
ou [Reference Wang32, §2.1] pour la justification des faits suivants. Soit
![]() $\sigma \in {\mathcal {B}}{\mathcal {T}}_{k}$
un simplexe de type
$\sigma \in {\mathcal {B}}{\mathcal {T}}_{k}$
un simplexe de type
![]() $(e_0, e_1,\cdots , e_k)$
et posons
$(e_0, e_1,\cdots , e_k)$
et posons
L’ouvert
![]() ${\mathbb {H}}_{K,\sigma }^d$
est un affinoïde, admettant un modèle entier
${\mathbb {H}}_{K,\sigma }^d$
est un affinoïde, admettant un modèle entier
![]() ${\mathbb {H}}_{{\mathcal {O}}_K,\sigma }^d =\operatorname {\mathrm {Spf}} (\hat {A}_\sigma )$
où
${\mathbb {H}}_{{\mathcal {O}}_K,\sigma }^d =\operatorname {\mathrm {Spf}} (\hat {A}_\sigma )$
où
![]() $\hat {A}_\sigma $
est le complété p-adique de
$\hat {A}_\sigma $
est le complété p-adique de
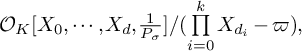 ${\mathcal {O}}_K [X_0,\cdots , X_d,\frac {1}{P_\sigma }]/(\prod \limits _{{\substack {i=0}}}^{k}{X_{d_{i}}}-\varpi ),$
pour un certain polynôme
${\mathcal {O}}_K [X_0,\cdots , X_d,\frac {1}{P_\sigma }]/(\prod \limits _{{\substack {i=0}}}^{k}{X_{d_{i}}}-\varpi ),$
pour un certain polynôme
![]() $P_{\sigma }\in {\mathcal {O}}_K[X_0,...,X_d]$
qui est décrit dans [Reference Wang32, §2.1] ou dans [Reference Junger26, §1.5]. Tous ces modèles locaux
$P_{\sigma }\in {\mathcal {O}}_K[X_0,...,X_d]$
qui est décrit dans [Reference Wang32, §2.1] ou dans [Reference Junger26, §1.5]. Tous ces modèles locaux
![]() ${\mathbb {H}}_{{\mathcal {O}}_K,{\sigma }}^d$
se recollent pour donner lieu à un modèle global
${\mathbb {H}}_{{\mathcal {O}}_K,{\sigma }}^d$
se recollent pour donner lieu à un modèle global
![]() ${\mathbb {H}}_{{\mathcal {O}}_K}^d=\bigcup _\sigma {\mathbb {H}}_{{\mathcal {O}}_K,{\sigma }}^d$
de
${\mathbb {H}}_{{\mathcal {O}}_K}^d=\bigcup _\sigma {\mathbb {H}}_{{\mathcal {O}}_K,{\sigma }}^d$
de
![]() ${\mathbb {H}}_{K}^d$
. La fibre spéciale
${\mathbb {H}}_{K}^d$
. La fibre spéciale
![]() ${\mathbb {H}}_{\mathbb {F}}^{d}$
de ce modèle admet une décomposition similaire
${\mathbb {H}}_{\mathbb {F}}^{d}$
de ce modèle admet une décomposition similaire
![]() $\mathrm{idem} =\bigcup _\sigma {\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d$
qui vérifie
$\mathrm{idem} =\bigcup _\sigma {\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d$
qui vérifie
![]() ${\mathbb {H}}_{K,{\sigma }}^d=]{\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d[$
. Nous ne nous servirons ici que du cas où
${\mathbb {H}}_{K,{\sigma }}^d=]{\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d[$
. Nous ne nous servirons ici que du cas où
![]() $\sigma =s$
est un sommet. L’algèbre
$\sigma =s$
est un sommet. L’algèbre
![]() $\hat {A}_s$
est alors le complété p-adique de
$\hat {A}_s$
est alors le complété p-adique de
 $$ \begin{align} {\mathcal{O}}_K [X_0,\cdots, X_{d-1},\frac{1}{\prod_{a=(a_i)_i\in {\mathbb{F}}^{d+1}\backslash \{0\}} (\tilde{a}_0 X_0+\cdots \tilde{a}_{d-1}X_{d-1}+ \tilde{a}_d)}] \end{align} $$
$$ \begin{align} {\mathcal{O}}_K [X_0,\cdots, X_{d-1},\frac{1}{\prod_{a=(a_i)_i\in {\mathbb{F}}^{d+1}\backslash \{0\}} (\tilde{a}_0 X_0+\cdots \tilde{a}_{d-1}X_{d-1}+ \tilde{a}_d)}] \end{align} $$
avec
![]() $\tilde {a}=(\tilde {a}_i)_i $
un relevé de a dans
$\tilde {a}=(\tilde {a}_i)_i $
un relevé de a dans
![]() ${\mathcal {O}}_K$
. Pour
${\mathcal {O}}_K$
. Pour
![]() ${\mathbb {H}}_{K,\mathring {\sigma }}^d$
, il s’agit de l’ouvert (dans une base adaptée)
${\mathbb {H}}_{K,\mathring {\sigma }}^d$
, il s’agit de l’ouvert (dans une base adaptée)
avec
![]() $M_{-1}=\varpi M_k$
. Considérons les ouverts
$M_{-1}=\varpi M_k$
. Considérons les ouverts
 $$\begin{align*}C_r&= \{x=(x_1,\cdots, x_r)\in {\mathbb{B}}^r_K|\, \forall a\in {\mathcal{O}}^{r+1}_K\backslash \varpi {\mathcal{O}}^{r+1}_K, \ 1=|\left\langle (1, x),a \right\rangle| \},\\A_k&=\{y=(y_0,\cdots, y_{k-1})\in {\mathbb{B}}^k_K|\, 1>|y_{k-1}|>\cdots>|y_0|>|\varpi|\}\end{align*}$$
$$\begin{align*}C_r&= \{x=(x_1,\cdots, x_r)\in {\mathbb{B}}^r_K|\, \forall a\in {\mathcal{O}}^{r+1}_K\backslash \varpi {\mathcal{O}}^{r+1}_K, \ 1=|\left\langle (1, x),a \right\rangle| \},\\A_k&=\{y=(y_0,\cdots, y_{k-1})\in {\mathbb{B}}^k_K|\, 1>|y_{k-1}|>\cdots>|y_0|>|\varpi|\}\end{align*}$$
et les morphismes
 $$ \begin{align*}{\mathbb{H}}_{K,\mathring{\sigma}}^d &\rightarrow C_{e_i -1}, \,\, [z_0,\cdots, z_d] \mapsto (\frac{ z_{d_{i-1}+1} }{ z_{d_{i-1}} },\frac{ z_{d_{i-1}+2} }{ z_{d_{i-1}} },\cdots, \frac{ z_{d_{i}-1} }{ z_{d_{i-1}} })\text{ et }\\{\mathbb{H}}_{K,\mathring{\sigma}}^d &\rightarrow A_k,\,\, [z_0,\cdots, z_d] \mapsto (\frac{ z_{d_{0}} }{ z_{d} },\frac{ z_{d_{1}} }{ z_{d} },\cdots, \frac{ z_{d_{k-1}} }{ z_{d} }).\end{align*} $$
$$ \begin{align*}{\mathbb{H}}_{K,\mathring{\sigma}}^d &\rightarrow C_{e_i -1}, \,\, [z_0,\cdots, z_d] \mapsto (\frac{ z_{d_{i-1}+1} }{ z_{d_{i-1}} },\frac{ z_{d_{i-1}+2} }{ z_{d_{i-1}} },\cdots, \frac{ z_{d_{i}-1} }{ z_{d_{i-1}} })\text{ et }\\{\mathbb{H}}_{K,\mathring{\sigma}}^d &\rightarrow A_k,\,\, [z_0,\cdots, z_d] \mapsto (\frac{ z_{d_{0}} }{ z_{d} },\frac{ z_{d_{1}} }{ z_{d} },\cdots, \frac{ z_{d_{k-1}} }{ z_{d} }).\end{align*} $$
Il est montré dans [Reference De Shalit10, 6.4] que les morphismes ci-dessus induisent un isomorphisme
 $$\begin{align*}{\mathbb{H}}_{K,\mathring{\sigma}}^d \cong A_k \times \prod\limits_{{\substack{i=0}}}^{k}{C_{e_i-1}}\cong A_k \times C_\sigma.\end{align*}$$
$$\begin{align*}{\mathbb{H}}_{K,\mathring{\sigma}}^d \cong A_k \times \prod\limits_{{\substack{i=0}}}^{k}{C_{e_i-1}}\cong A_k \times C_\sigma.\end{align*}$$
De même, on peut définir des ouverts en fibre spéciale
![]() ${\mathbb {H}}_{{\mathbb {F}},\mathring {\sigma }}^d={\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d\setminus \bigcup _{\sigma '\subsetneq \sigma }{\mathbb {H}}_{{\mathbb {F}},{\sigma '}}^d$
telle que
${\mathbb {H}}_{{\mathbb {F}},\mathring {\sigma }}^d={\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d\setminus \bigcup _{\sigma '\subsetneq \sigma }{\mathbb {H}}_{{\mathbb {F}},{\sigma '}}^d$
telle que
![]() ${\mathbb {H}}_{K,\mathring {\sigma }}^d=]{\mathbb {H}}_{{\mathbb {F}},\mathring {\sigma }}^d[$
.
${\mathbb {H}}_{K,\mathring {\sigma }}^d=]{\mathbb {H}}_{{\mathbb {F}},\mathring {\sigma }}^d[$
.
Remarque 3.1. Nous avons introduit précédemment une décomposition en somme adapté au simplexe:
avec
![]() $N_i=\left \langle f_{d_{i-1}+1},\cdots , f_{d_{i}} \right \rangle $
. En particulier, un vecteur unimodulaire a est dans
$N_i=\left \langle f_{d_{i-1}+1},\cdots , f_{d_{i}} \right \rangle $
. En particulier, un vecteur unimodulaire a est dans
![]() $M_i$
si et seulement si la projection sur
$M_i$
si et seulement si la projection sur
![]() $ N_{i+1} \oplus \cdots \oplus N_k$
est divisible par
$ N_{i+1} \oplus \cdots \oplus N_k$
est divisible par
![]() $\varpi $
. Ainsi tout vecteur a de
$\varpi $
. Ainsi tout vecteur a de
![]() $M_i$
peut s’écrire sous la forme
$M_i$
peut s’écrire sous la forme
![]() $a=a_1+a_2$
avec
$a=a_1+a_2$
avec
![]() $a_1\in N_i$
,
$a_1\in N_i$
,
![]() $a_2\in M_{i-1}$
et on a d’après la description des morphismes ci-dessus:
$a_2\in M_{i-1}$
et on a d’après la description des morphismes ci-dessus:
3.4 Géométrie de la fibre spéciale de
 ${\mathbb {H}}_{{\mathcal {O}}_K}^d$
${\mathbb {H}}_{{\mathcal {O}}_K}^d$
Si s est un sommet de
![]() ${\mathcal {B}}{\mathcal {T}}$
on note
${\mathcal {B}}{\mathcal {T}}$
on note
l’étoile ouverte, respectivement fermée de s. Pour un simplexe
![]() $\sigma $
, on note
$\sigma $
, on note
En prenant des intersections, des unions et des complémentaires d’espaces de la forme
![]() ${\mathbb {H}}_{K,{\sigma }}^d$
,
${\mathbb {H}}_{K,{\sigma }}^d$
,
![]() ${\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d$
, on peut encore définir des espaces
${\mathbb {H}}_{{\mathbb {F}},{\sigma }}^d$
, on peut encore définir des espaces
![]() ${\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(\sigma )}^d$
,
${\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(\sigma )}^d$
,
![]() ${\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(\sigma )}^d$
(idem pour
${\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(\sigma )}^d$
(idem pour
![]() $\operatorname {\mathrm {Fst}}$
) tels que
$\operatorname {\mathrm {Fst}}$
) tels que
![]() ${\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(\sigma )}^d=]{\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(\sigma )}^d[$
.
${\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(\sigma )}^d=]{\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(\sigma )}^d[$
.
Les composantes irréductibles de la fibre spéciale de
![]() ${\mathbb {H}}_{{\mathcal {O}}_K}^d$
sont les fermés
${\mathbb {H}}_{{\mathcal {O}}_K}^d$
sont les fermés
![]() ${\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d$
et sont donc indexées par l’ensemble des sommets de
${\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d$
et sont donc indexées par l’ensemble des sommets de
![]() ${\mathcal {B}}{\mathcal {T}}_0$
. On obtient ainsi un recouvrement admissible
${\mathcal {B}}{\mathcal {T}}_0$
. On obtient ainsi un recouvrement admissible
![]() $({\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(s)}^d)_{s\in {\mathcal {B}}{\mathcal {T}}_0}=(]{\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d[)_{s\in {\mathcal {B}}{\mathcal {T}}_0}$
de
$({\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(s)}^d)_{s\in {\mathcal {B}}{\mathcal {T}}_0}=(]{\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d[)_{s\in {\mathcal {B}}{\mathcal {T}}_0}$
de
![]() ${\mathbb {H}}_K^d$
dont les intersections d’ouverts sont de la forme
${\mathbb {H}}_K^d$
dont les intersections d’ouverts sont de la forme
![]() ${\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(\sigma )}^d$
pour
${\mathbb {H}}_{K,\operatorname {\mathrm {Ost}}(\sigma )}^d$
pour
![]() $\sigma \subset {\mathcal {B}}{\mathcal {T}}$
un simplexe. En fibre spéciale, le lieu lisse de cette intersection est l’ouvert
$\sigma \subset {\mathcal {B}}{\mathcal {T}}$
un simplexe. En fibre spéciale, le lieu lisse de cette intersection est l’ouvert
 $$\begin{align*}{\mathbb{H}}_{{\mathbb{F}},\operatorname{\mathrm{Ost}}(\sigma)}^d\backslash \bigcup\limits_{{\substack{s\notin \sigma}}}^{}{{\mathbb{H}}_{{\mathbb{F}},\operatorname{\mathrm{Ost}}(s)}^d}={\mathbb{H}}_{{\mathbb{F}},\mathring\sigma}^d \end{align*}$$
$$\begin{align*}{\mathbb{H}}_{{\mathbb{F}},\operatorname{\mathrm{Ost}}(\sigma)}^d\backslash \bigcup\limits_{{\substack{s\notin \sigma}}}^{}{{\mathbb{H}}_{{\mathbb{F}},\operatorname{\mathrm{Ost}}(s)}^d}={\mathbb{H}}_{{\mathbb{F}},\mathring\sigma}^d \end{align*}$$
car
![]() $\mathring {\sigma }=\sigma \backslash \bigcup \limits _{{\substack {\sigma '\subsetneq \sigma }}}^{}{\sigma '}$
. En particulier, le lieu lisse d’une composante irréductible est
$\mathring {\sigma }=\sigma \backslash \bigcup \limits _{{\substack {\sigma '\subsetneq \sigma }}}^{}{\sigma '}$
. En particulier, le lieu lisse d’une composante irréductible est
où H parcourt l’ensemble des hyperplans
![]() ${\mathbb {F}}$
-rationnels (cf (1)). De plus,
${\mathbb {F}}$
-rationnels (cf (1)). De plus,
![]() ${\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d$
est une compactification qui s’obtient comme suit ([Reference Genestier17, sous-section III.1.] ou [Reference Wang33, 4.1.2]). Posons
${\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d$
est une compactification qui s’obtient comme suit ([Reference Genestier17, sous-section III.1.] ou [Reference Wang33, 4.1.2]). Posons
![]() $Y_0 ={\mathbb {P}}_{{\mathbb {F}}}^d$
et construisons par éclatements successifs une suite d’espaces
$Y_0 ={\mathbb {P}}_{{\mathbb {F}}}^d$
et construisons par éclatements successifs une suite d’espaces
Supposons que l’on ait préalablement construit
![]() $Y_0 , \cdots , Y_i$
. On a des morphismes
$Y_0 , \cdots , Y_i$
. On a des morphismes
![]() $p_i :Y_i \to Y_{i-1}$
et
$p_i :Y_i \to Y_{i-1}$
et
![]() $\tilde {p}_i =p_i\circ \cdots \circ p_1 : Y_i \to Y_{0}$
. On pose
$\tilde {p}_i =p_i\circ \cdots \circ p_1 : Y_i \to Y_{0}$
. On pose
![]() $Z_i$
le transformé strict par
$Z_i$
le transformé strict par
![]() $\tilde {p}_i$
de l’union des espaces de codimension
$\tilde {p}_i$
de l’union des espaces de codimension
![]() $i + 1$
dans
$i + 1$
dans
![]() $Y_0$
. On définit
$Y_0$
. On définit
![]() $Y_{i+1}$
comme l’éclaté de
$Y_{i+1}$
comme l’éclaté de
![]() $Y_i$
suivant
$Y_i$
suivant
![]() $Z_i$
. Alors, on a
$Z_i$
. Alors, on a
![]() $Y_d\cong {\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d$
.
$Y_d\cong {\mathbb {H}}_{{\mathbb {F}},\operatorname {\mathrm {Ost}}(s)}^d$
.
3.5 Interprétation modulaire de l’espace de Drinfeld
Pour construire le premier revêtement de l’espace de Drinfeld, nous avons besoin d’une interprétation modulaire de cet espace, ce qui demande quelques notions et notations.
Rappelons que D est une K-algèbre centrale à division, de dimension
![]() $(d+1)^2$
et d’invariant
$(d+1)^2$
et d’invariant
![]() $\frac {1}{d+1}$
et considérons
$\frac {1}{d+1}$
et considérons
![]() ${\mathcal {O}}_{(d+1)}$
l’anneau des entiers d’une extension non-ramifiée de K, de degré
${\mathcal {O}}_{(d+1)}$
l’anneau des entiers d’une extension non-ramifiée de K, de degré
![]() $d+1$
contenue dans D. Si A est une
$d+1$
contenue dans D. Si A est une
![]() ${\mathcal {O}}_K$
-algèbre, un
${\mathcal {O}}_K$
-algèbre, un
![]() ${\mathcal {O}}_D$
-module formel sur
${\mathcal {O}}_D$
-module formel sur
![]() $\mathrm {Spec}(A)$
(ou, plus simplement, sur A) est un groupe formel X sur A muni d’une action de
$\mathrm {Spec}(A)$
(ou, plus simplement, sur A) est un groupe formel X sur A muni d’une action de
![]() ${\mathcal {O}}_D$
, notée
${\mathcal {O}}_D$
, notée
![]() $\iota : {\mathcal {O}}_D \to \mathrm {End}(X)$
, qui est compatible avec l’action naturelle de
$\iota : {\mathcal {O}}_D \to \mathrm {End}(X)$
, qui est compatible avec l’action naturelle de
![]() ${\mathcal {O}}_K$
sur l’espace tangent
${\mathcal {O}}_K$
sur l’espace tangent
![]() $\mathrm {Lie}(F)$
(i.e., pour a dans
$\mathrm {Lie}(F)$
(i.e., pour a dans
![]() ${\mathcal {O}}_K$
${\mathcal {O}}_K$
![]() $d\iota (a)$
est la multiplication par a dans
$d\iota (a)$
est la multiplication par a dans
![]() $\mathrm {Lie}(F)$
). Le
$\mathrm {Lie}(F)$
). Le
![]() ${\mathcal {O}}_D$
-module formel X est dit spécial si
${\mathcal {O}}_D$
-module formel X est dit spécial si
![]() $\mathrm {Lie}(X)$
est un
$\mathrm {Lie}(X)$
est un
![]() ${\mathcal {O}}_{(d+1)}\otimes _{{\mathcal {O}}_K} A$
-module localement libre de rang
${\mathcal {O}}_{(d+1)}\otimes _{{\mathcal {O}}_K} A$
-module localement libre de rang
![]() $1$
. On a le résultat classique suivant:
$1$
. On a le résultat classique suivant:
Proposition 3.2. Sur un corps algébriquement clos de caractéristique p, il existe, à isogénie près, un unique
![]() ${\mathcal {O}}_D$
-module formel spécial de dimension
${\mathcal {O}}_D$
-module formel spécial de dimension
![]() $d+1$
et de
$d+1$
et de
![]() $({\mathcal {O}}_K$
-)hauteur
$({\mathcal {O}}_K$
-)hauteur
![]() $(d+1)^2$
.
$(d+1)^2$
.
On notera
![]() $\Phi _{\overline {{\mathbb {F}}}}$
l’unique (à isogénie près)
$\Phi _{\overline {{\mathbb {F}}}}$
l’unique (à isogénie près)
![]() ${\mathcal {O}}_D$
-module formel spécial sur
${\mathcal {O}}_D$
-module formel spécial sur
![]() $\overline {{\mathbb {F}}}$
de dimension
$\overline {{\mathbb {F}}}$
de dimension
![]() $d+1$
et hauteur
$d+1$
et hauteur
![]() $(d+1)^2$
(l’entier d étant fixé par la suite, nous ne le faisons pas apparaître dans la notation
$(d+1)^2$
(l’entier d étant fixé par la suite, nous ne le faisons pas apparaître dans la notation
![]() $\Phi _{\overline {{\mathbb {F}}}}$
).
$\Phi _{\overline {{\mathbb {F}}}}$
).
Soit
![]() $\mathrm {Nilp}_{{\mathcal {O}}_{\breve {K}}}$
la catégorie des
$\mathrm {Nilp}_{{\mathcal {O}}_{\breve {K}}}$
la catégorie des
![]() ${\mathcal {O}}_{\breve {K}}$
-algèbres sur lesquelles
${\mathcal {O}}_{\breve {K}}$
-algèbres sur lesquelles
![]() $\varpi $
est nilpotent. Considérons le foncteur
$\varpi $
est nilpotent. Considérons le foncteur
![]() ${\mathcal {G}}^{Dr} : \mathrm {Nilp}_{{\mathcal {O}}_{\breve {K}}} \to \mathrm {Ens}$
envoyant
${\mathcal {G}}^{Dr} : \mathrm {Nilp}_{{\mathcal {O}}_{\breve {K}}} \to \mathrm {Ens}$
envoyant
![]() $A\in \mathrm {Nilp}_{{\mathcal {O}}_{\breve {K}}}$
sur l’ensemble des classes d’isomorphisme de triplets
$A\in \mathrm {Nilp}_{{\mathcal {O}}_{\breve {K}}}$
sur l’ensemble des classes d’isomorphisme de triplets
![]() $(\psi , X, \rho )$
avec:
$(\psi , X, \rho )$
avec:
-
•
 $\psi : \overline {{\mathbb {F}}} \to A/ \varpi A$
est un
$\psi : \overline {{\mathbb {F}}} \to A/ \varpi A$
est un
 ${\mathbb {F}}$
-morphisme,
${\mathbb {F}}$
-morphisme, -
• X est un
 ${\mathcal {O}}_D$
-module formel spécial de dimension
${\mathcal {O}}_D$
-module formel spécial de dimension
 $d+1$
et de hauteur
$d+1$
et de hauteur
 $(d+1)^2$
sur A,
$(d+1)^2$
sur A, -
•
 $\rho : \Phi _{\overline {{\mathbb {F}}}} \otimes _{\overline {{\mathbb {F}}}, \psi } A/ \varpi A \to X_{A/ \varpi A}$
est une quasi-isogénie de hauteur zéro.
$\rho : \Phi _{\overline {{\mathbb {F}}}} \otimes _{\overline {{\mathbb {F}}}, \psi } A/ \varpi A \to X_{A/ \varpi A}$
est une quasi-isogénie de hauteur zéro.
Le théorème fondamental suivant, à la base de toute la théorie, est dû à Drinfeld:
Théorème 3.3 [Reference Drinfel’d14].
Le foncteur
![]() ${\mathcal {G}}^{Dr}$
est représentable par
${\mathcal {G}}^{Dr}$
est représentable par
![]() ${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d$
.
${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d$
.
Remarque 3.4. On définit le foncteur
![]() $\tilde {{\mathcal {G}}}^{Dr}$
de la même manière que
$\tilde {{\mathcal {G}}}^{Dr}$
de la même manière que
![]() ${\mathcal {G}}^{Dr}$
mais en ne fixant plus la hauteur de la quasi-isogénie
${\mathcal {G}}^{Dr}$
mais en ne fixant plus la hauteur de la quasi-isogénie
![]() $\rho $
. Alors
$\rho $
. Alors
![]() $\tilde {{\mathcal {G}}}^{Dr}$
est, lui aussi, représentable par un schéma formel
$\tilde {{\mathcal {G}}}^{Dr}$
est, lui aussi, représentable par un schéma formel
![]() $\widehat {{\mathcal {M}}}^0_{Dr}$
sur
$\widehat {{\mathcal {M}}}^0_{Dr}$
sur
![]() $ \operatorname {\mathrm {Spf}} ({\mathcal {O}}_K)$
, qui se décompose
$ \operatorname {\mathrm {Spf}} ({\mathcal {O}}_K)$
, qui se décompose
où
![]() ${\mathcal {G}}^{Dr,(h)}$
est défini comme précédemment en imposant que la quasi-isogénie
${\mathcal {G}}^{Dr,(h)}$
est défini comme précédemment en imposant que la quasi-isogénie
![]() $\rho $
soit de hauteur
$\rho $
soit de hauteur
![]() $(d+1)h$
. Chacun des
$(d+1)h$
. Chacun des
![]() ${\mathcal {G}}^{Dr,(h)}$
est alors isomorphe (non canoniquement) au foncteur
${\mathcal {G}}^{Dr,(h)}$
est alors isomorphe (non canoniquement) au foncteur
![]() ${\mathcal {G}}^{Dr}$
, ce qui induit un isomorphisme non-canonique
${\mathcal {G}}^{Dr}$
, ce qui induit un isomorphisme non-canonique
3.6 La tour de Drinfeld
On note
![]() $\mathfrak {X}$
le
$\mathfrak {X}$
le
![]() ${\mathcal {O}}_D$
-module formel spécial universel sur
${\mathcal {O}}_D$
-module formel spécial universel sur
![]() ${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d$
(cf. th. 3.3) et
${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d$
(cf. th. 3.3) et
![]() $\tilde {{\mathfrak {X}}}$
le module formel spécial universel déduit de la représentabilité de
$\tilde {{\mathfrak {X}}}$
le module formel spécial universel déduit de la représentabilité de
![]() $\tilde {{\mathcal {G}}}^{Dr}$
. Pour tout entier
$\tilde {{\mathcal {G}}}^{Dr}$
. Pour tout entier
![]() $n\geq 1$
, l’action de
$n\geq 1$
, l’action de
![]() $\Pi _D^n$
induit une isogénie de
$\Pi _D^n$
induit une isogénie de
![]() ${\mathfrak {X}}$
et de
${\mathfrak {X}}$
et de
![]() $\tilde {{\mathfrak {X}}}$
. Le schéma en groupes
$\tilde {{\mathfrak {X}}}$
. Le schéma en groupes
![]() $\mathfrak {X}[ \Pi _D^n] = \ker ( \mathfrak {X} \xrightarrow {\Pi _D^n} \mathfrak {X})$
(resp.
$\mathfrak {X}[ \Pi _D^n] = \ker ( \mathfrak {X} \xrightarrow {\Pi _D^n} \mathfrak {X})$
(resp.
![]() $\tilde {{\mathfrak {X}}}[\Pi _D^n]$
) est fini plat, de rang
$\tilde {{\mathfrak {X}}}[\Pi _D^n]$
) est fini plat, de rang
![]() $q^{n(d+1)}$
sur
$q^{n(d+1)}$
sur
![]() ${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d$
(resp.
${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d$
(resp.
![]() $\widehat {{\mathcal {M}}}^0_{Dr}$
).
$\widehat {{\mathcal {M}}}^0_{Dr}$
).
On note
![]() $\Sigma ^0={\mathbb {H}}^d_{\breve {K}}$
et
$\Sigma ^0={\mathbb {H}}^d_{\breve {K}}$
et
![]() ${\mathcal {M}}^0_{Dr}=(\widehat {{\mathcal {M}}}^0_{Dr})^{\mathrm { rig}}\cong {\mathbb {H}}^d_{\breve {K}}\times {\mathbb {Z}}$
. Pour
${\mathcal {M}}^0_{Dr}=(\widehat {{\mathcal {M}}}^0_{Dr})^{\mathrm { rig}}\cong {\mathbb {H}}^d_{\breve {K}}\times {\mathbb {Z}}$
. Pour
![]() $n\geq 1$
on définit
$n\geq 1$
on définit
Les morphismes d’oubli
![]() $\Sigma ^n \to \Sigma ^0$
et
$\Sigma ^n \to \Sigma ^0$
et
![]() ${\mathcal {M}}^n_{Dr}\to {\mathcal {M}}^0_{Dr}$
définissent des revêtements finis étales de groupe de GaloisFootnote
2
${\mathcal {M}}^n_{Dr}\to {\mathcal {M}}^0_{Dr}$
définissent des revêtements finis étales de groupe de GaloisFootnote
2
![]() ${\mathcal {O}}_D^{*}/(1+ \Pi ^n_D {\mathcal {O}}_D)$
. On a encore des isomorphismes non-canoniques
${\mathcal {O}}_D^{*}/(1+ \Pi ^n_D {\mathcal {O}}_D)$
. On a encore des isomorphismes non-canoniques
![]() ${\mathcal {M}}^n_{Dr}\cong \Sigma ^n\times {\mathbb {Z}}$
et les revêtements respectent ces décompositions.
${\mathcal {M}}^n_{Dr}\cong \Sigma ^n\times {\mathbb {Z}}$
et les revêtements respectent ces décompositions.
Le groupe G s’identifie au groupe des quasi-isogénies de
![]() ${\mathfrak {X}}$
, il agit donc naturellement sur chaque niveau de la tour
${\mathfrak {X}}$
, il agit donc naturellement sur chaque niveau de la tour
![]() $({\mathcal {M}}^n_{Dr})_{n\geq 0}$
. De même, le groupe
$({\mathcal {M}}^n_{Dr})_{n\geq 0}$
. De même, le groupe
![]() ${\mathcal {O}}_D^{*}$
permute les points de
${\mathcal {O}}_D^{*}$
permute les points de
![]() $\Pi ^n_D $
-torsion et
$\Pi ^n_D $
-torsion et
![]() ${\mathcal {O}}_D^{*}$
agit sur
${\mathcal {O}}_D^{*}$
agit sur
![]() ${\mathcal {M}}^n_{Dr}$
à travers son quotient
${\mathcal {M}}^n_{Dr}$
à travers son quotient
![]() ${\mathcal {O}}_D^{*}/(1+ \Pi ^n_D {\mathcal {O}}_D)\simeq \mathrm { Gal}({\mathcal {M}}^n_{Dr}/{\mathcal {M}}^0_{Dr})$
. Ces deux actions commutent entre elle et les revêtements
${\mathcal {O}}_D^{*}/(1+ \Pi ^n_D {\mathcal {O}}_D)\simeq \mathrm { Gal}({\mathcal {M}}^n_{Dr}/{\mathcal {M}}^0_{Dr})$
. Ces deux actions commutent entre elle et les revêtements
![]() ${\mathcal {M}}^n_{Dr}\to {\mathcal {M}}^0_{Dr}$
sont G-équivariants. En revanche, le revêtement
${\mathcal {M}}^n_{Dr}\to {\mathcal {M}}^0_{Dr}$
sont G-équivariants. En revanche, le revêtement
![]() $\Sigma ^n\to \Sigma ^{0}$
est seulement
$\Sigma ^n\to \Sigma ^{0}$
est seulement
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)$
-équivariant.Footnote
3
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)$
-équivariant.Footnote
3
3.7 Le premier revêtement
Nous nous intéressons désormais au cas
![]() $n=1$
. On peut encore définir une flèche de réduction
$n=1$
. On peut encore définir une flèche de réduction
![]() $\nu $
de
$\nu $
de
![]() $\Sigma ^1$
vers l’immeuble de Bruhat-Tits
$\Sigma ^1$
vers l’immeuble de Bruhat-Tits
![]() ${\mathcal {B}}{\mathcal {T}}$
s’inscrivant dans le diagramme:
${\mathcal {B}}{\mathcal {T}}$
s’inscrivant dans le diagramme:

Pour tout sous-complexe simplicial
![]() $T \subseteq {\mathcal {B}} {\mathcal {T}}$
, on note
$T \subseteq {\mathcal {B}} {\mathcal {T}}$
, on note
Le groupe de Galois de
![]() $\Sigma ^1$
est
$\Sigma ^1$
est
![]() ${\mathbb {F}}_{q^{d+1}}^{*}$
. Ce groupe est cyclique et son cardinal
${\mathbb {F}}_{q^{d+1}}^{*}$
. Ce groupe est cyclique et son cardinal
est premier à p. C’est un revêtement modérément ramifié et ces deux propriétés joueront un rôle central dans la suite. Le schéma
![]() $\mathfrak {X}[ \Pi _D]$
est, en particulier, un schéma en
$\mathfrak {X}[ \Pi _D]$
est, en particulier, un schéma en
![]() ${\mathbb {F}}_p$
-espaces vectoriels et la condition que
${\mathbb {F}}_p$
-espaces vectoriels et la condition que
![]() $\mathfrak {X}$
soit spécial entraîne que
$\mathfrak {X}$
soit spécial entraîne que
![]() $\mathfrak {X}[ \Pi _D]$
est un schéma de Raynaud. Pour énoncer les conséquences de cette observation, introduisons quelques notations.
$\mathfrak {X}[ \Pi _D]$
est un schéma de Raynaud. Pour énoncer les conséquences de cette observation, introduisons quelques notations.
Écrivons
 $$ \begin{align*}\tilde{u}_1(z)=(-1)^{d}\prod_{a \in ({\mathbb{F}})^{d+1} \backslash \{ 0 \}}a_0z_0 +\cdots +a_d z_d\in {\mathscr{O}}({\mathbb{A}}^{d+1}_{{\mathbb{F}}}\backslash\{0\}).\end{align*} $$
$$ \begin{align*}\tilde{u}_1(z)=(-1)^{d}\prod_{a \in ({\mathbb{F}})^{d+1} \backslash \{ 0 \}}a_0z_0 +\cdots +a_d z_d\in {\mathscr{O}}({\mathbb{A}}^{d+1}_{{\mathbb{F}}}\backslash\{0\}).\end{align*} $$
Si on fixe
![]() $b\in ({\mathbb {F}})^{d+1} \backslash \{ 0 \}$
, on construit
$b\in ({\mathbb {F}})^{d+1} \backslash \{ 0 \}$
, on construit
![]() $u_1(z)=(b_0z_0 +\cdots +b_d z_d)^{-N}\tilde {u}_1$
une fonction inversible de
$u_1(z)=(b_0z_0 +\cdots +b_d z_d)^{-N}\tilde {u}_1$
une fonction inversible de
![]() ${\mathbb {H}}_{{\mathbb {F}},s}^d\cong {\mathbb {P}}_{ {\mathbb {F}}}^d\backslash \bigcup _{H\in {\mathcal {H}}_1} H$
pour s le sommet standard de
${\mathbb {H}}_{{\mathbb {F}},s}^d\cong {\mathbb {P}}_{ {\mathbb {F}}}^d\backslash \bigcup _{H\in {\mathcal {H}}_1} H$
pour s le sommet standard de
![]() ${\mathcal {B}}{\mathcal {T}}$
. Notons que la projection de
${\mathcal {B}}{\mathcal {T}}$
. Notons que la projection de
![]() $u_1$
dans
$u_1$
dans
![]() ${\mathscr {O}}^{*}({\mathbb {H}}_{{\mathbb {F}},s}^d)/ ({\mathscr {O}}^{*}({\mathbb {H}}_{{\mathbb {F}},s}^d))^N$
ne dépends pas du choix de b et celui-ci n’aura donc pas d’incidence sur les résultats à suivre. Pour simplifier, nous pourrons prendre
${\mathscr {O}}^{*}({\mathbb {H}}_{{\mathbb {F}},s}^d)/ ({\mathscr {O}}^{*}({\mathbb {H}}_{{\mathbb {F}},s}^d))^N$
ne dépends pas du choix de b et celui-ci n’aura donc pas d’incidence sur les résultats à suivre. Pour simplifier, nous pourrons prendre
![]() $b=(0,\cdots ,0,1)$
. On peut aussi relever
$b=(0,\cdots ,0,1)$
. On peut aussi relever
![]() $u_1$
en une fonction inversible dans
$u_1$
en une fonction inversible dans
![]() ${\mathscr {O}}^{*}({\mathbb {H}}_{{\mathcal {O}}_{\breve {K}},s}^d)$
voire même dans
${\mathscr {O}}^{*}({\mathbb {H}}_{{\mathcal {O}}_{\breve {K}},s}^d)$
voire même dans
![]() ${\mathscr {O}}^{*}({\mathbb {H}}^d_{\breve {K},\operatorname {\mathrm {Ost}}(s)})$
que l’on notera encore
${\mathscr {O}}^{*}({\mathbb {H}}^d_{\breve {K},\operatorname {\mathrm {Ost}}(s)})$
que l’on notera encore
![]() $u_1$
.
$u_1$
.
En utilisant la classification des schémas de Raynaud, on a d’après [Reference Junger26, Théorème 4.9 et Remarque 4.10]Footnote
4
(cet énoncé étend les résultats de Teitelbaum [Reference Teitelbaum30, Théorème 5] pour
![]() $d=1$
et de Wang [Reference Wang32, Lemme 2.3.7.] pour d quelconque):
$d=1$
et de Wang [Reference Wang32, Lemme 2.3.7.] pour d quelconque):
Théorème 3.5. Il existe
![]() $u\in {\mathscr {O}}^{*}({\mathbb {H}}^d_{\breve {K}})$
vérifiant
$u\in {\mathscr {O}}^{*}({\mathbb {H}}^d_{\breve {K}})$
vérifiant
![]() $u\equiv u_1 \pmod {{\mathscr {O}}^{*}({\mathbb {H}}^d_{\breve {K},\operatorname {\mathrm {Ost}}(s)})^N}$
telle que
$u\equiv u_1 \pmod {{\mathscr {O}}^{*}({\mathbb {H}}^d_{\breve {K},\operatorname {\mathrm {Ost}}(s)})^N}$
telle que
En particulier,
![]() $\Sigma ^1_{\operatorname {\mathrm {Ost}}(s)}\cong {\mathbb {H}}^d_{\breve {K},\operatorname {\mathrm {Ost}}(s)}((\varpi u_1)^{\frac {1}{N}})$
.
$\Sigma ^1_{\operatorname {\mathrm {Ost}}(s)}\cong {\mathbb {H}}^d_{\breve {K},\operatorname {\mathrm {Ost}}(s)}((\varpi u_1)^{\frac {1}{N}})$
.
Remarque 3.6. Notons que le résultat précédent ne décrit pas l’action de
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)\varpi ^{{\mathbb {Z}}}=\operatorname {\mathrm {Stab}}_{G}(\operatorname {\mathrm {Ost}}(s))$
. Toutefois, d’après [Reference Junger26, Remarque 4.12], toutes les actions possibles sur
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)\varpi ^{{\mathbb {Z}}}=\operatorname {\mathrm {Stab}}_{G}(\operatorname {\mathrm {Ost}}(s))$
. Toutefois, d’après [Reference Junger26, Remarque 4.12], toutes les actions possibles sur
![]() $\Sigma ^1$
commutant avec le revêtement se déduisent l’une de l’autre en tordant par un caractère
$\Sigma ^1$
commutant avec le revêtement se déduisent l’une de l’autre en tordant par un caractère
Nous déterminerons l’action provenant de l’interprétation modulaire dans 6.3.
4 Cohomologie des variétés de Deligne-Lusztig
4.1 Variétés de Deligne-Lusztig
Considérons les groupes algébriques
![]() $G=\operatorname {\mathrm {GL}}_{d+1, \overline {{\mathbb {F}}}}$
et
$G=\operatorname {\mathrm {GL}}_{d+1, \overline {{\mathbb {F}}}}$
et
![]() $G_0=\operatorname {\mathrm {GL}}_{d+1,{\mathbb {F}}}$
, ainsi que le morphisme de Frobenius F défini par
$G_0=\operatorname {\mathrm {GL}}_{d+1,{\mathbb {F}}}$
, ainsi que le morphisme de Frobenius F défini par
![]() $(a_{i,j})_{i,j} \mapsto (a_{i,j}^q)_{i,j}$
. Soit B le sous-groupe des matrices triangulaires supérieures, T le tore des matrices diagonales, U le sous-groupe de B des matrices unipotentes.
$(a_{i,j})_{i,j} \mapsto (a_{i,j}^q)_{i,j}$
. Soit B le sous-groupe des matrices triangulaires supérieures, T le tore des matrices diagonales, U le sous-groupe de B des matrices unipotentes.
On identifie le groupe de Weyl
![]() $W=N_G(T)/T$
à
$W=N_G(T)/T$
à
![]() ${\mathfrak {S}}_{d+1}$
par le biais des matrices de permutation. Soit w la matrice de permutation associée au cycle
${\mathfrak {S}}_{d+1}$
par le biais des matrices de permutation. Soit w la matrice de permutation associée au cycle
![]() $(0, 1, \dots , d) \in {\mathfrak {S}}_{d+1}$
. On définit
$(0, 1, \dots , d) \in {\mathfrak {S}}_{d+1}$
. On définit
 $$\begin{align*}Y(w)&:= \{ gU \in G/U |\,\, g^{-1}F(g) \in U w U \} \text{ et }\\X(w)&:= \{ gB \in G/B |\,\, g^{-1}F(g) \in B w B \}. \end{align*}$$
$$\begin{align*}Y(w)&:= \{ gU \in G/U |\,\, g^{-1}F(g) \in U w U \} \text{ et }\\X(w)&:= \{ gB \in G/B |\,\, g^{-1}F(g) \in B w B \}. \end{align*}$$
On a un diagramme commutatif:

Le groupe
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})=G(\overline {{\mathbb {F}}})^{F=1}$
agit sur
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})=G(\overline {{\mathbb {F}}})^{F=1}$
agit sur
![]() $Y(w)$
et
$Y(w)$
et
![]() $X(w)$
par multiplication à gauche. Le groupe fini commutatif
$X(w)$
par multiplication à gauche. Le groupe fini commutatif
agit librement (par multiplication à droite) sur
![]() $Y(w)$
. La flèche
$Y(w)$
. La flèche
![]() $\pi $
est un revêtement fini étale qui induit un isomorphisme
$\pi $
est un revêtement fini étale qui induit un isomorphisme
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
-équivariant
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
-équivariant
On peut rendre ces objets plus explicites comme suit [Reference Deligne and Lusztig11, 2.2]. D’une part
![]() $T^{wF}$
s’identifie à
$T^{wF}$
s’identifie à
![]() ${\mathbb {F}}_{q^{d+1}}^{*}$
via l’application
${\mathbb {F}}_{q^{d+1}}^{*}$
via l’application
![]() $x \in {\mathbb {F}}_{q^{d+1}}^{*} \mapsto \mathrm {diag}(x, Fx, \dots , F^dx)$
. D’autre part, considérons la variété
$x \in {\mathbb {F}}_{q^{d+1}}^{*} \mapsto \mathrm {diag}(x, Fx, \dots , F^dx)$
. D’autre part, considérons la variété
où H parcourt l’ensemble des hyperplans
![]() ${\mathbb {F}}$
-rationnels. Elle possède une action naturelle de
${\mathbb {F}}$
-rationnels. Elle possède une action naturelle de
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
. On rappelle que l’on a aussi construit dans la section précédente deux applications
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
. On rappelle que l’on a aussi construit dans la section précédente deux applications
![]() $\tilde {u}_1(z)\in {\mathscr {O}}({\mathbb {A}}^{d+1}_{{\mathbb {F}}}\backslash \{0\})$
et
$\tilde {u}_1(z)\in {\mathscr {O}}({\mathbb {A}}^{d+1}_{{\mathbb {F}}}\backslash \{0\})$
et
![]() $u_1(z)=\tilde {u}_1(z)/z_d^N\in {\mathscr {O}}^{*}(\Omega ^d_{{\mathbb {F}}})$
.
$u_1(z)=\tilde {u}_1(z)/z_d^N\in {\mathscr {O}}^{*}(\Omega ^d_{{\mathbb {F}}})$
.
Proposition 4.1. On a des identifications
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
-équivariantes entre
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
-équivariantes entre
![]() $X(w)$
et
$X(w)$
et
![]() $\Omega ^d_{{\mathbb {F}}}$
et entre
$\Omega ^d_{{\mathbb {F}}}$
et entre
![]() $Y(w)$
et
$Y(w)$
et
De plus,
![]() $\pi $
est induite par la projection naturelle
$\pi $
est induite par la projection naturelle
![]() ${\mathbb {A}}_{{\mathbb {F}}}^{d+1} \backslash \{ 0 \}\to {\mathbb {P}}_{{\mathbb {F}}}^{d}$
${\mathbb {A}}_{{\mathbb {F}}}^{d+1} \backslash \{ 0 \}\to {\mathbb {P}}_{{\mathbb {F}}}^{d}$
Remarque 4.2.
-
• En envoyant
 $(z_0,...,z_d)\in Y(w)$
sur
$(z_0,...,z_d)\in Y(w)$
sur
 $(z_d^{-1}, [z_0:\cdots :z_d])$
et
$(z_d^{-1}, [z_0:\cdots :z_d])$
et
 $(t,z=[z_0:\cdots: z_d])\in \Omega^d_{\mathbb{F}}(u_1^{1/N})$
sur
$(t,z=[z_0:\cdots: z_d])\in \Omega^d_{\mathbb{F}}(u_1^{1/N})$
sur
 $(\frac{z_0}{tz_d},\cdots,\frac{z_{d-1}}{tz_d}, t^{-1})$
sous l’identification précédente, on obtient un isomorphisme
$(\frac{z_0}{tz_d},\cdots,\frac{z_{d-1}}{tz_d}, t^{-1})$
sous l’identification précédente, on obtient un isomorphisme
 ${\mathbb {F}}_{q^{d+1}}^{*}$
-équivariant (le deuxième terme n’a pas d’action naturelle de
${\mathbb {F}}_{q^{d+1}}^{*}$
-équivariant (le deuxième terme n’a pas d’action naturelle de
 $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
…)
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
…)  $$ \begin{align*}Y(w)\simeq \Omega^d_{{\mathbb{F}}}(u_1^{1/N}).\end{align*} $$
$$ \begin{align*}Y(w)\simeq \Omega^d_{{\mathbb{F}}}(u_1^{1/N}).\end{align*} $$
-
• Comme dans la remarque 3.6, toutes les actions possibles de
 $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
sur
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
sur
 $ \Omega ^d_{{\mathbb {F}}}(u_1^{1/N})$
commutant avec le revêtement se déduisent l’une de l’autre en tordant par un caractère et le lemme 6.3 exhibe une identification naturelle avec l’ensemble des actions considérées dans 3.6. Dans 6.3, nous verrons que l’action provenant de l’interprétation modulaire de
$ \Omega ^d_{{\mathbb {F}}}(u_1^{1/N})$
commutant avec le revêtement se déduisent l’une de l’autre en tordant par un caractère et le lemme 6.3 exhibe une identification naturelle avec l’ensemble des actions considérées dans 3.6. Dans 6.3, nous verrons que l’action provenant de l’interprétation modulaire de $$\begin{align*}\chi \in \operatorname{\mathrm{Hom}} (\operatorname{\mathrm{GL}}_{d+1}({\mathcal{O}}_K),\ \mu_N(\Omega^d_{{\mathbb{F}}}))\cong{\mathbb{F}}^{*},\end{align*}$$
$$\begin{align*}\chi \in \operatorname{\mathrm{Hom}} (\operatorname{\mathrm{GL}}_{d+1}({\mathcal{O}}_K),\ \mu_N(\Omega^d_{{\mathbb{F}}}))\cong{\mathbb{F}}^{*},\end{align*}$$
 $\Sigma ^1$
et l’action naturelle sur
$\Sigma ^1$
et l’action naturelle sur
 $\operatorname {\mathrm {DL}}^d_{{\mathbb {F}}}$
coïncident sous cette bijection.
$\operatorname {\mathrm {DL}}^d_{{\mathbb {F}}}$
coïncident sous cette bijection.
Démonstration. On identifie
![]() $G/B$
à la variété des drapeaux complets de
$G/B$
à la variété des drapeaux complets de
![]() $(\overline {{\mathbb {F}}})^{d+1}$
. On vérifie facilement qu’un drapeau
$(\overline {{\mathbb {F}}})^{d+1}$
. On vérifie facilement qu’un drapeau
![]() $\{ 0 \} \subsetneq D_0 \subsetneq \dots \subsetneq D_{d}=(\overline {{\mathbb {F}}})^{d+1} $
est dans
$\{ 0 \} \subsetneq D_0 \subsetneq \dots \subsetneq D_{d}=(\overline {{\mathbb {F}}})^{d+1} $
est dans
![]() $X(w)$
si et seulement si pour tout i on a
$X(w)$
si et seulement si pour tout i on a
On obtient un plongement
![]() $X(w) \to {\mathbb {P}}_{{\mathbb {F}}}^{d}, (D_i) \mapsto D_0$
. La projection d’un point
$X(w) \to {\mathbb {P}}_{{\mathbb {F}}}^{d}, (D_i) \mapsto D_0$
. La projection d’un point
![]() $z=(z_0, \dots , z_d) \in (\overline {{\mathbb {F}}})^{d+1} \backslash \{ 0 \}$
est dans l’image de ce morphisme si et seulement si
$z=(z_0, \dots , z_d) \in (\overline {{\mathbb {F}}})^{d+1} \backslash \{ 0 \}$
est dans l’image de ce morphisme si et seulement si
![]() $(z, Fz, \dots , F^d z)$
est une base de
$(z, Fz, \dots , F^d z)$
est une base de
![]() $(\overline {{\mathbb {F}}})^{d+1}$
, ce qui revient à dire que
$(\overline {{\mathbb {F}}})^{d+1}$
, ce qui revient à dire que
![]() $\det ((z_i^{q^j})_{0\le i,j\le d})$
est non nul. Mais
$\det ((z_i^{q^j})_{0\le i,j\le d})$
est non nul. Mais
 $$\begin{align*}\det((z_i^{q^j})_{i,j})^{q-1}= \prod_{a \in ({\mathbb{F}})^{d+1} \backslash \{ 0 \}} l_{a}(z) =(-1)^{d}\tilde{u}_1(z).\end{align*}$$
$$\begin{align*}\det((z_i^{q^j})_{i,j})^{q-1}= \prod_{a \in ({\mathbb{F}})^{d+1} \backslash \{ 0 \}} l_{a}(z) =(-1)^{d}\tilde{u}_1(z).\end{align*}$$
On en déduit alors un isomorphisme
 $$ \begin{align*}X(w) \xrightarrow{\sim} {\mathbb{P}}_{{\mathbb{F}}}^d \backslash \bigcup_{H \in {\mathbb{P}}^d({\mathbb{F}})} H= \Omega^d_{{\mathbb{F}}}. \end{align*} $$
$$ \begin{align*}X(w) \xrightarrow{\sim} {\mathbb{P}}_{{\mathbb{F}}}^d \backslash \bigcup_{H \in {\mathbb{P}}^d({\mathbb{F}})} H= \Omega^d_{{\mathbb{F}}}. \end{align*} $$
La variété
![]() $ G/U$
classifie les paires
$ G/U$
classifie les paires
![]() $((D_i)_i, (e_i)_i)$
avec
$((D_i)_i, (e_i)_i)$
avec
![]() $(D_i)_i$
un drapeau et
$(D_i)_i$
un drapeau et
![]() $e_i\in D_i/ D_{i-1}$
. Une paire
$e_i\in D_i/ D_{i-1}$
. Une paire
![]() $((D_i)_i, (e_i)_i)$
est dans
$((D_i)_i, (e_i)_i)$
est dans
![]() $Y(w)$
si et seulement si
$Y(w)$
si et seulement si
![]() $(D_i)_i\in X(w)$
et
$(D_i)_i\in X(w)$
et
Ainsi la flèche
![]() $((D_i)_i, (e_i)_i)\mapsto e_0$
induit un plongement
$((D_i)_i, (e_i)_i)\mapsto e_0$
induit un plongement
![]() $Y(w)\to {\mathbb {A}}_{{\mathbb {F}}}^{d+1} \backslash \{ 0 \}$
rendant le diagramme suivant commutatif:
$Y(w)\to {\mathbb {A}}_{{\mathbb {F}}}^{d+1} \backslash \{ 0 \}$
rendant le diagramme suivant commutatif:

Un point
![]() $x=(z_0, \dots , z_d) \in {\mathbb {A}}_{ {\mathbb {F}}}^{d+1} \backslash \{ 0 \}$
est dans l’image de ce morphisme si et seulement si
$x=(z_0, \dots , z_d) \in {\mathbb {A}}_{ {\mathbb {F}}}^{d+1} \backslash \{ 0 \}$
est dans l’image de ce morphisme si et seulement si
![]() $\det ((z_i^{q^j})_{0\le i,j\le d})=(-1)^d \det (F\cdot (z_i^{q^j})_{0\le i,j\le d})$
. Cela revient à écrire
$\det ((z_i^{q^j})_{0\le i,j\le d})=(-1)^d \det (F\cdot (z_i^{q^j})_{0\le i,j\le d})$
. Cela revient à écrire
4.2 Cohomologie étale des variétés de Deligne-Lusztig
On note
![]() $\operatorname {\mathrm {DL}}^d_{\overline {{\mathbb {F}}}}$
l’extension des scalaires de
$\operatorname {\mathrm {DL}}^d_{\overline {{\mathbb {F}}}}$
l’extension des scalaires de
![]() $\operatorname {\mathrm {DL}}_{{\mathbb {F}}}^d$
à
$\operatorname {\mathrm {DL}}_{{\mathbb {F}}}^d$
à
![]() $\overline {{\mathbb {F}}}$
. Soit
$\overline {{\mathbb {F}}}$
. Soit
![]() $l\ne p$
un nombre premier, nous allons rappeler la description de la partie cuspidale de la cohomologie l-adique à support compact de
$l\ne p$
un nombre premier, nous allons rappeler la description de la partie cuspidale de la cohomologie l-adique à support compact de
![]() $\operatorname {\mathrm {DL}}^d_{\overline {{\mathbb {F}}}}$
.
$\operatorname {\mathrm {DL}}^d_{\overline {{\mathbb {F}}}}$
.
Soit
![]() $\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to \overline {{\mathbb {Q}}}_l^{*}$
un caractère, on dit que
$\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to \overline {{\mathbb {Q}}}_l^{*}$
un caractère, on dit que
![]() $\theta $
est primitif s’il ne se factorise pas par la norme
$\theta $
est primitif s’il ne se factorise pas par la norme
![]() ${\mathbb {F}}_{q^{d+1}}^{*}\to {\mathbb {F}}_{q^e}^{*}$
pour tout diviseur propre e de
${\mathbb {F}}_{q^{d+1}}^{*}\to {\mathbb {F}}_{q^e}^{*}$
pour tout diviseur propre e de
![]() $d+1$
. Si M est un
$d+1$
. Si M est un
![]() $ \overline {\mathbb {Q}}_l[{\mathbb {F}}_{q^{d+1}}^{*}]$
-module on note
$ \overline {\mathbb {Q}}_l[{\mathbb {F}}_{q^{d+1}}^{*}]$
-module on note
Si
![]() $\pi $
est une représentation de
$\pi $
est une représentation de
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
, on dit que
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
, on dit que
![]() $\pi $
est cuspidale si
$\pi $
est cuspidale si
![]() $\pi ^{N({\mathbb {F}})}=0$
pour tout radical unipotent N d’un parabolique propre de
$\pi ^{N({\mathbb {F}})}=0$
pour tout radical unipotent N d’un parabolique propre de
![]() $\operatorname {\mathrm {GL}}_{d+1}$
. La théorie de Deligne-Lusztig (ou celle de Green dans notre cas particulier) fournit:
$\operatorname {\mathrm {GL}}_{d+1}$
. La théorie de Deligne-Lusztig (ou celle de Green dans notre cas particulier) fournit:
Théorème 4.3. Soit
![]() $\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to \overline {{\mathbb {Q}}}_l^{*}$
un caractère.
$\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to \overline {{\mathbb {Q}}}_l^{*}$
un caractère.
a) Si
![]() $\theta $
est primitif, alors
$\theta $
est primitif, alors
![]() $\mathrm {H}^{i}_{\acute {\mathrm {e}}\mathrm {t},c}(DL_{\bar{\mathbb{F}}}^d, \bar{\mathbb{Q}}_l)[\theta]$
est nul pour
$\mathrm {H}^{i}_{\acute {\mathrm {e}}\mathrm {t},c}(DL_{\bar{\mathbb{F}}}^d, \bar{\mathbb{Q}}_l)[\theta]$
est nul pour
![]() $i\ne d$
et
$i\ne d$
et
est une
![]() $\operatorname {\mathrm {GL}}_{d+1}( {\mathbb {F}})$
-représentation irréductible, cuspidale, de dimension
$\operatorname {\mathrm {GL}}_{d+1}( {\mathbb {F}})$
-représentation irréductible, cuspidale, de dimension
![]() $(q-1)(q^2-1) \dots (q^d-1)$
. Toutes les représentations cuspidales sont ainsi obtenues.
$(q-1)(q^2-1) \dots (q^d-1)$
. Toutes les représentations cuspidales sont ainsi obtenues.
b) Si
![]() $\theta $
n’est pas primitif, aucune représentation cuspidale n’intervient dans
$\theta $
n’est pas primitif, aucune représentation cuspidale n’intervient dans
![]() $\bigoplus _{i}\mathrm { H}^{i}_{\acute {\mathrm {e}}\mathrm {t},c}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d, \overline {{\mathbb {Q}}}_l)[\theta ]$
.
$\bigoplus _{i}\mathrm { H}^{i}_{\acute {\mathrm {e}}\mathrm {t},c}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d, \overline {{\mathbb {Q}}}_l)[\theta ]$
.
Démonstration. Voir [Reference Deligne and Lusztig11, cor. 6.3], [Reference Deligne and Lusztig11, th. 7.3], [Reference Deligne and Lusztig11, prop. 7.4], [Reference Deligne and Lusztig11, prop. 8.3], [Reference Deligne and Lusztig11, cor. 9.9], pour ces résultats classiques.
Ainsi, la partie cuspidale
![]() $\mathrm {H}^{*}_{\acute {\mathrm {e}}\mathrm {t},c}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d, \overline {{\mathbb {Q}}}_l)_{\mathrm {cusp}}$
de
$\mathrm {H}^{*}_{\acute {\mathrm {e}}\mathrm {t},c}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d, \overline {{\mathbb {Q}}}_l)_{\mathrm {cusp}}$
de
![]() $\mathrm {H}^{*}_{\acute {\mathrm {e}}\mathrm {t},c}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d, \overline {{\mathbb {Q}}}_l)$
est concentrée en degré d, où elle est donnée par
$\mathrm {H}^{*}_{\acute {\mathrm {e}}\mathrm {t},c}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d, \overline {{\mathbb {Q}}}_l)$
est concentrée en degré d, où elle est donnée par
![]() $\bigoplus _{\theta } \overline {\pi }_{\theta ,l}\otimes \theta $
, la somme directe portant sur tous les caractères primitifs.
$\bigoplus _{\theta } \overline {\pi }_{\theta ,l}\otimes \theta $
, la somme directe portant sur tous les caractères primitifs.
Remarque 4.4. (voir [Reference Deligne and Lusztig11, 6.3] et [Reference Yoshida34, Proposition 6.8.(ii) et remarques]) Soit
![]() $N=q^{d+1}-1$
et fixons un isomorphisme
$N=q^{d+1}-1$
et fixons un isomorphisme
![]() ${\mathbb {F}}_{q^{d+1}}^{*}\simeq {\mathbb {Z}}/N{\mathbb {Z}}$
et
${\mathbb {F}}_{q^{d+1}}^{*}\simeq {\mathbb {Z}}/N{\mathbb {Z}}$
et
![]() ${\mathbb {Z}}/N{\mathbb {Z}}^{\vee }\simeq {\mathbb {Z}}/N{\mathbb {Z}}$
. Soient
${\mathbb {Z}}/N{\mathbb {Z}}^{\vee }\simeq {\mathbb {Z}}/N{\mathbb {Z}}$
. Soient
![]() $\theta _{j_1}$
et
$\theta _{j_1}$
et
![]() $\theta _{j_2}$
deux caractères primitifs vus comme des éléments de
$\theta _{j_2}$
deux caractères primitifs vus comme des éléments de
![]() ${\mathbb {Z}}/N{\mathbb {Z}}$
via
${\mathbb {Z}}/N{\mathbb {Z}}$
via
![]() $j_1$
,
$j_1$
,
![]() $j_2$
, les représentations
$j_2$
, les représentations
![]() $\overline {\pi }_{\theta _{j_1}}$
et
$\overline {\pi }_{\theta _{j_1}}$
et
![]() $\overline {\pi }_{\theta _{j_2}}$
sont isomorphes si et seulement si il existe un entier n tel que
$\overline {\pi }_{\theta _{j_2}}$
sont isomorphes si et seulement si il existe un entier n tel que
![]() $j_1= q^n j_2$
dans
$j_1= q^n j_2$
dans
![]() ${\mathbb {Z}}/N{\mathbb {Z}}$
.
${\mathbb {Z}}/N{\mathbb {Z}}$
.
4.3 Cohomologie rigide des variétés de Deligne-Lusztig
Nous aurons besoin d’un analogue des résultats présentés dans le paragraphe précédent pour la cohomologie rigide. Cela a été fait par Grosse-Klönne dans [Reference Grosse-Klönne22]. Si
![]() $\theta : {\mathbb {F}}^{*}_{q^{d+1}}\to \overline {K}^{*}$
est un caractère, posons
$\theta : {\mathbb {F}}^{*}_{q^{d+1}}\to \overline {K}^{*}$
est un caractère, posons
où
et où
![]() $M[\theta ]$
désigne comme avant la composante
$M[\theta ]$
désigne comme avant la composante
![]() $\theta $
-isotypique de M.
$\theta $
-isotypique de M.
Théorème 4.5. Fixons un premier
![]() $l\ne p$
et un isomorphisme
$l\ne p$
et un isomorphisme
![]() $\overline {K} \cong \overline {{\mathbb {Q}}}_l$
. Si
$\overline {K} \cong \overline {{\mathbb {Q}}}_l$
. Si
![]() $\theta $
est un caractère primitif, alors
$\theta $
est un caractère primitif, alors
est isomorphe en tant que
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
-module à
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}})$
-module à
![]() $\overline {\pi }_{\theta ,l}$
, en particulier c’est une représentation irréductible cuspidale.
$\overline {\pi }_{\theta ,l}$
, en particulier c’est une représentation irréductible cuspidale.
Démonstration. Cela se fait en trois étapes; cf. [Reference Grosse-Klönne22, 4.5]. Dans un premier temps, on montre [Reference Grosse-Klönne22, 3.1] que les
![]() $\overline {K}[\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}}) \times {\mathbb {F}}^{*}_{q^{d+1}}]$
-modules virtuels
$\overline {K}[\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}}) \times {\mathbb {F}}^{*}_{q^{d+1}}]$
-modules virtuels
coïncident. Il s’agit d’une comparaison standard des formules des traces de Lefschetz en cohomologies étale l-adique et rigide. Dans un deuxième temps (et c’est bien la partie délicate du résultat), on montre que
![]() $\bigoplus _{i}\mathrm {H}^{i}_{\mathrm {rig},c}(\operatorname {\mathrm {DL}}_{{\mathbb {F}}}^d/ \overline {K})[ \theta ]$
est bien concentré en degré d; cf. [Reference Grosse-Klönne22, th. 2.3]. On peut alors conclure en utilisant le théorème 4.3.
$\bigoplus _{i}\mathrm {H}^{i}_{\mathrm {rig},c}(\operatorname {\mathrm {DL}}_{{\mathbb {F}}}^d/ \overline {K})[ \theta ]$
est bien concentré en degré d; cf. [Reference Grosse-Klönne22, th. 2.3]. On peut alors conclure en utilisant le théorème 4.3.
5 Cohomologie de de Rham et revêtements cycliques modérés
Dans ce chapitre L sera une extension non ramifiée de K, donc
![]() $\varpi $
en est une uniformisante. Toutes les cohomologies de de Rham seront calculées sur le complexe surconvergeant ie. nous écrirons par abus
$\varpi $
en est une uniformisante. Toutes les cohomologies de de Rham seront calculées sur le complexe surconvergeant ie. nous écrirons par abus
![]() $\mathrm { H}^{*}_{\mathrm {dR}} (X)$
pour tout espace analytique X au lieu de
$\mathrm { H}^{*}_{\mathrm {dR}} (X)$
pour tout espace analytique X au lieu de
![]() $\mathrm {H}^{*}_{\mathrm {dR}} (X^{\dagger })$
.
$\mathrm {H}^{*}_{\mathrm {dR}} (X^{\dagger })$
.
5.1 Réduction semi-stable généralisée
Soit
![]() ${\mathcal {X}}$
un schéma formel topologiquement de type fini sur
${\mathcal {X}}$
un schéma formel topologiquement de type fini sur
![]() $\operatorname {\mathrm {Spf}} ({\mathcal {O}}_L)$
, de fibre générique
$\operatorname {\mathrm {Spf}} ({\mathcal {O}}_L)$
, de fibre générique
![]() ${\mathcal {X}}_\eta $
et de fibre spéciale
${\mathcal {X}}_\eta $
et de fibre spéciale
![]() ${\mathcal {X}}_s$
. On a une flèche de spécialisation
${\mathcal {X}}_s$
. On a une flèche de spécialisation
![]() $\operatorname {\mathrm {Sp}}: {\mathcal {X}}_\eta \rightarrow {\mathcal {X}}_s$
. Pour tout sous-schéma
$\operatorname {\mathrm {Sp}}: {\mathcal {X}}_\eta \rightarrow {\mathcal {X}}_s$
. Pour tout sous-schéma
![]() $Z\subset {\mathcal {X}}_s$
on note
$Z\subset {\mathcal {X}}_s$
on note
![]() $]Z[_{{\mathcal {X}}}$
le tube de Z dans
$]Z[_{{\mathcal {X}}}$
le tube de Z dans
![]() ${\mathcal {X}}_\eta $
(i.e., l’espace analytique
${\mathcal {X}}_\eta $
(i.e., l’espace analytique
On dit que
![]() ${\mathcal {X}}$
est de réduction semi-stable généralisée s’il existe un recouvrement ouvert (Zariski)
${\mathcal {X}}$
est de réduction semi-stable généralisée s’il existe un recouvrement ouvert (Zariski)
![]() ${\mathcal {X}}=\bigcup \limits _{{\substack {t\in T}}}^{}{U_t}$
et un jeu de morphismes étales (pour certains
${\mathcal {X}}=\bigcup \limits _{{\substack {t\in T}}}^{}{U_t}$
et un jeu de morphismes étales (pour certains
![]() $r\leq d$
et
$r\leq d$
et
![]() $\alpha _i\geq 1$
)
$\alpha _i\geq 1$
)
Dans ce cas, quitte à rétrécir les ouverts
![]() $U_t$
et à prendre r minimal, on peut supposer que les composantes irréductibles de la fibre spéciale
$U_t$
et à prendre r minimal, on peut supposer que les composantes irréductibles de la fibre spéciale
![]() $\overline {U}_t$
de
$\overline {U}_t$
de
![]() $U_t$
sont les
$U_t$
sont les
![]() $V(\overline {x}^{*}_i)$
pour
$V(\overline {x}^{*}_i)$
pour
![]() $i\leq r$
avec
$i\leq r$
avec
![]() $\overline {x}^{*}_i =\overline {\varphi }_t (\overline {x}_i)$
. Elles ont les multiplicités
$\overline {x}^{*}_i =\overline {\varphi }_t (\overline {x}_i)$
. Elles ont les multiplicités
![]() $\alpha _i$
. On dit que
$\alpha _i$
. On dit que
![]() ${\mathcal {X}}$
est de réduction semi-stable si de plus tous les
${\mathcal {X}}$
est de réduction semi-stable si de plus tous les
![]() $\alpha _i$
valent
$\alpha _i$
valent
![]() $1$
. Dans ce cas, les fibres spéciales
$1$
. Dans ce cas, les fibres spéciales
![]() $\overline {U}_t$
sont réduites.
$\overline {U}_t$
sont réduites.
5.2 Enoncé du résultat principal
Soit
![]() ${\mathcal {X}}$
un schéma formel sur
${\mathcal {X}}$
un schéma formel sur
![]() $\operatorname {\mathrm {Spf}} ({\mathcal {O}}_L)$
, de réduction semi-stable généralisée, de fibre générique
$\operatorname {\mathrm {Spf}} ({\mathcal {O}}_L)$
, de réduction semi-stable généralisée, de fibre générique
![]() ${\mathcal {X}}_\eta $
et de fibre spéciale
${\mathcal {X}}_\eta $
et de fibre spéciale
![]() ${\mathcal {X}}_s$
. On note
${\mathcal {X}}_s$
. On note
![]() $(Y_i)_{i\in I}$
l’ensemble des composantes irréductibles de
$(Y_i)_{i\in I}$
l’ensemble des composantes irréductibles de
![]() ${\mathcal {X}}_s$
. On suppose que le recouvrement
${\mathcal {X}}_s$
. On suppose que le recouvrement
![]() ${\mathcal {X}}_s=\bigcup \limits _{{\substack {i\in I}}}^{}{Y_i}$
est localement fini (i.e., pour toute partie finie J de I, les composantes
${\mathcal {X}}_s=\bigcup \limits _{{\substack {i\in I}}}^{}{Y_i}$
est localement fini (i.e., pour toute partie finie J de I, les composantes
![]() $Y_j$
pour
$Y_j$
pour
![]() $j\in J$
n’intersectent qu’un nombre fini de composantes irréductibles de
$j\in J$
n’intersectent qu’un nombre fini de composantes irréductibles de
![]() ${\mathcal {X}}_s$
). Si J est un sous-ensemble de I, on note
${\mathcal {X}}_s$
). Si J est un sous-ensemble de I, on note
Le but de cette section est de prouver le théorème suivant:
Théorème 5.1. Soient
![]() ${\mathcal {X}}$
semi-stable généralisé et
${\mathcal {X}}$
semi-stable généralisé et
![]() $(Y_i)_{i\in I}$
comme ci-dessus, et soit
$(Y_i)_{i\in I}$
comme ci-dessus, et soit
![]() $\pi : {\mathcal {T}}\rightarrow {\mathcal {X}}_\eta $
un revêtement étale de groupe de Galois
$\pi : {\mathcal {T}}\rightarrow {\mathcal {X}}_\eta $
un revêtement étale de groupe de Galois
![]() $\mu _n$
avec n premier à p. Pour toute partie finie J de I la flèche de restriction induit un isomorphisme
$\mu _n$
avec n premier à p. Pour toute partie finie J de I la flèche de restriction induit un isomorphisme
 $$\begin{align*}\mathrm{ H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J[_{\mathcal{X}}))\xrightarrow[]{\sim} \mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_{J}\backslash \bigcup_{i\notin J}Y_i[_{\mathcal{X}})).\end{align*}$$
$$\begin{align*}\mathrm{ H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J[_{\mathcal{X}}))\xrightarrow[]{\sim} \mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_{J}\backslash \bigcup_{i\notin J}Y_i[_{\mathcal{X}})).\end{align*}$$
si
![]() ${\mathcal {X}}$
est de réduction semi-stable (non généralisée) ou
${\mathcal {X}}$
est de réduction semi-stable (non généralisée) ou
![]() $n=1$
(i.e.,
$n=1$
(i.e.,
![]() ${\mathcal {T}}={\mathcal {X}}_\eta $
).
${\mathcal {T}}={\mathcal {X}}_\eta $
).
Remarque 5.2.
-
1. Si
 ${\mathcal {X}}$
est de réduction semi-stable (non généralisée) et
${\mathcal {X}}$
est de réduction semi-stable (non généralisée) et
 $n=1$
(i.e.,
$n=1$
(i.e.,
 ${\mathcal {T}}={\mathcal {X}}_\eta $
) le théorème ci-dessus a été démontré par Grosse-Klönne [Reference Grosse-Klönne20, Theorem 2.4.]. Il s’agit d’un point crucial dans sa preuve de la finitude de la cohomologie rigide. Le principal intérêt de notre généralisation est la présence du revêtement cyclique
${\mathcal {T}}={\mathcal {X}}_\eta $
) le théorème ci-dessus a été démontré par Grosse-Klönne [Reference Grosse-Klönne20, Theorem 2.4.]. Il s’agit d’un point crucial dans sa preuve de la finitude de la cohomologie rigide. Le principal intérêt de notre généralisation est la présence du revêtement cyclique
 $\pi $
de la fibre générique de
$\pi $
de la fibre générique de
 ${\mathcal {X}}_\eta $
.
${\mathcal {X}}_\eta $
. -
2. Si de plus
 ${\mathcal {X}}$
est algébrisable et
${\mathcal {X}}$
est algébrisable et
 $|J|=1$
, le résultat [Reference Zheng35, Lemme 5.6] est un analogue en cohomologie étale l-adique du théorème ci-dessus.
$|J|=1$
, le résultat [Reference Zheng35, Lemme 5.6] est un analogue en cohomologie étale l-adique du théorème ci-dessus.
Comme dans la preuve originale, on procède en deux étapes. On applique dans un premier temps un certain nombre de réductions assez techniques (cf. 5.5 et 5.6) pour se ramener à l’étude des revêtements de couronnes. Ces étapes sont similaires à la démonstration de Grosse-Klönne, qui utilise des recouvrements bien choisis et la suite spectrale de Cech. Dans notre cas, on reprend les mêmes recouvrements de
![]() ${\mathcal {X}}_\eta $
puis on les tire en arrière par
${\mathcal {X}}_\eta $
puis on les tire en arrière par
![]() $\pi $
pour étudier l’espace
$\pi $
pour étudier l’espace
![]() ${\mathcal {T}}$
. Le seul point technique à adapter dans ces réductions est la vérification que l’espace final obtenu est bien décrit par un revêtement de couronnes (voir 5.16).
${\mathcal {T}}$
. Le seul point technique à adapter dans ces réductions est la vérification que l’espace final obtenu est bien décrit par un revêtement de couronnes (voir 5.16).
La deuxième étape de la preuve est le calcul de la cohomologie de de Rham d’un revêtement cyclique modéré d’une couronne. Cela se fait par des calculs directs sur le complexe de de Rham, et fournit une description très explicite de ces groupes de cohomologie. Pour énoncer le résultat nous avons besoin de quelques notations. Considérons la couronne
avec
![]() $s_1,\ldots,s_d,r_1,\ldots,r_d\in |\bar{K}^*|$
tels que
$s_1,\ldots,s_d,r_1,\ldots,r_d\in |\bar{K}^*|$
tels que
![]() $s_i\leq r_i$
pour tout i et un revêtement de Kummer de la forme
$s_i\leq r_i$
pour tout i et un revêtement de Kummer de la forme
![]() $\mathcal{T}=X((\lambda x^\beta)^{1/n})$
avec n premier à p,
$\mathcal{T}=X((\lambda x^\beta)^{1/n})$
avec n premier à p,
![]() $\lambda\in L^*$
et
$\lambda\in L^*$
et
![]() $\beta\in\mathbb{Z}^d$
. Les hypothéses sur
$\beta\in\mathbb{Z}^d$
. Les hypothéses sur
![]() $\mathcal{T}$
sont loisibles, puisque nous allons voir que tout revêtement
$\mathcal{T}$
sont loisibles, puisque nous allons voir que tout revêtement
![]() $\pi : {\mathcal {T}}\to X$
galoisien cyclique d’ordre n est de cette forme. On dispose donc sur
$\pi : {\mathcal {T}}\to X$
galoisien cyclique d’ordre n est de cette forme. On dispose donc sur
![]() ${\mathcal {T}}$
d’une racine n-ième t de
${\mathcal {T}}$
d’une racine n-ième t de
![]() $\lambda x^\beta $
. On définit enfin
$\lambda x^\beta $
. On définit enfin
 $$ \begin{align*}\pi_0 =\mathrm{PGCD}(n,\beta_1, \cdots, \beta_d), \, \tilde{n}=\frac{n}{\pi_0}, \,\tilde{\beta}=\frac{\beta}{\pi_0}, \, t_0=\frac{t^{\tilde{n}}}{x^{\tilde{\beta}}}.\end{align*} $$
$$ \begin{align*}\pi_0 =\mathrm{PGCD}(n,\beta_1, \cdots, \beta_d), \, \tilde{n}=\frac{n}{\pi_0}, \,\tilde{\beta}=\frac{\beta}{\pi_0}, \, t_0=\frac{t^{\tilde{n}}}{x^{\tilde{\beta}}}.\end{align*} $$
Enfin, si
![]() $q\ge 1$
et
$q\ge 1$
et
![]() $I=\left \lbrace i_1<\cdots < i_q\right \rbrace $
on pose
$I=\left \lbrace i_1<\cdots < i_q\right \rbrace $
on pose
Théorème 5.3. Avec les notations ci-dessus, on a des isomorphismes naturels
et
 $$\begin{align*}\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}})\simeq \bigoplus\limits_{{\substack{i=0}}}^{\pi_0 -1}{t_0^i\bigoplus\limits_{{\substack{I}}}^{}{L\cdot d\log (x_I)}} \cong\bigoplus\limits_{{\substack{i=0}}}^{\pi_0 -1}{t_0^i\mathrm{H}^{q}_{\mathrm{dR}}(X)}\end{align*}$$
$$\begin{align*}\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}})\simeq \bigoplus\limits_{{\substack{i=0}}}^{\pi_0 -1}{t_0^i\bigoplus\limits_{{\substack{I}}}^{}{L\cdot d\log (x_I)}} \cong\bigoplus\limits_{{\substack{i=0}}}^{\pi_0 -1}{t_0^i\mathrm{H}^{q}_{\mathrm{dR}}(X)}\end{align*}$$
où I parcours les parties de ![]() de cardinal q dans les sommes précédentes.
de cardinal q dans les sommes précédentes.
Remarque 5.4.
-
1. On déduit facilement du théorème que si
 $X'\subset X$
sont deux couronnes et si
$X'\subset X$
sont deux couronnes et si
 ${\mathcal {T}}\to X$
,
${\mathcal {T}}\to X$
,
 ${\mathcal {T}}'\to X'$
sont deux revêtements compatibles (ie.
${\mathcal {T}}'\to X'$
sont deux revêtements compatibles (ie.
 ${\mathcal {T}}' ={\mathcal {T}}\times _X X'$
) alors la flèche de restriction
${\mathcal {T}}' ={\mathcal {T}}\times _X X'$
) alors la flèche de restriction
 $\mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}})\rightarrow \mathrm {H}^{*}_{\mathrm {dR}} ({{\mathcal {T}}'})$
est un isomorphisme qui respecte la décomposition en parties isotypiques.
$\mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}})\rightarrow \mathrm {H}^{*}_{\mathrm {dR}} ({{\mathcal {T}}'})$
est un isomorphisme qui respecte la décomposition en parties isotypiques. -
2. En fait, tous ces résultats sont vrais pour une classe plus générale d’espaces, que l’on appellera tores monômiaux. Nous aurons besoin de ce degré de généralité et nous renvoyons à 5.6, 5.8 et 5.10 pour les énoncés dans ce cadre.
5.3 Tores monômiaux et leurs revêtements cycliques modérés
Définition 5.5. On appellera tore monômial de dimension d un L-espace analytique X de la formeFootnote 5
pour
![]() $s_i\leq r_i\in |\overline {K}^{*}|$
,
$s_i\leq r_i\in |\overline {K}^{*}|$
,
![]() $\alpha =(\alpha _1,...,\alpha _d)\in {\mathbb {N}}^d$
et
$\alpha =(\alpha _1,...,\alpha _d)\in {\mathbb {N}}^d$
et
![]() $\rho \le \mu \in [s^{\alpha }, r^{\alpha }]\cap |\overline {K}^{*}|$
).
$\rho \le \mu \in [s^{\alpha }, r^{\alpha }]\cap |\overline {K}^{*}|$
).
On appelle tore monômial semi-ouvert un espace défini par les mêmes inégalités qu’un tore monômial, mais potentiellement strictes. Nous souhaitons étendre un résultat de Berkovich [Reference Berkovich1, Lemma 3.3] au cas des tores monômiaux.
Proposition 5.6. Soit X un tore monômial de dimension d (semi-ouvert), S un espace K-analytique, n un entier premier à p. La projection canonique
![]() $\varphi : X_S:=X\times S \to S$
induit un isomorphisme
$\varphi : X_S:=X\times S \to S$
induit un isomorphisme
Démonstration. Soit X un tore monômial et
![]() $s,r,\alpha ,\rho ,\mu $
les données associées. Nous allons montrer le résultat par récurrence sur la dimension d. Si
$s,r,\alpha ,\rho ,\mu $
les données associées. Nous allons montrer le résultat par récurrence sur la dimension d. Si
![]() $d=1$
, tous les tores monômiaux sont des couronnes qui ont été traitées dans [Reference Berkovich1, Lemma 3.3] (on peut aussi appliquer [Reference Junger25, Lemme 4.4.] puis la suite exacte de Kummer).
$d=1$
, tous les tores monômiaux sont des couronnes qui ont été traitées dans [Reference Berkovich1, Lemma 3.3] (on peut aussi appliquer [Reference Junger25, Lemme 4.4.] puis la suite exacte de Kummer).
Soit
![]() $d>1$
, en projetant sur les
$d>1$
, en projetant sur les
![]() $d-1$
premières coordonnées, on obtient un morphisme
$d-1$
premières coordonnées, on obtient un morphisme
![]() $\psi : X\to Y$
vers le tore monômial:
$\psi : X\to Y$
vers le tore monômial:
avec
![]() $\overline {\alpha }=(\alpha _1 ,\cdots , \alpha _{d-1}) $
. Soient
$\overline {\alpha }=(\alpha _1 ,\cdots , \alpha _{d-1}) $
. Soient
![]() $u: Y_S\to S$
les projections naturelles, alors
$u: Y_S\to S$
les projections naturelles, alors
![]() $u\circ \psi =\varphi $
, donc
$u\circ \psi =\varphi $
, donc
Par hypothèse de récurrence et la suite spectrale de Leray il suffit d’établir les isomorphismes
 $$\begin{align*}R^q \psi_* \mu_n=\begin{cases} \mu_n & \mathrm{si}\ q=0\\ \mu_n (-1) & \mathrm{si}\ q=1\\ 0 & \mathrm{si}\ q>1\end{cases}.\end{align*}$$
$$\begin{align*}R^q \psi_* \mu_n=\begin{cases} \mu_n & \mathrm{si}\ q=0\\ \mu_n (-1) & \mathrm{si}\ q=1\\ 0 & \mathrm{si}\ q>1\end{cases}.\end{align*}$$
Notons que
![]() $R^q\psi _* \mu _n$
est un faisceau surconvergent (puisque les faisceaux constants le sont et que cette propriété est stable par image directe et twist à la Tate), on peut donc tester les isomorphismes ci-dessus fibre à fibre. Les tiges du faisceau
$R^q\psi _* \mu _n$
est un faisceau surconvergent (puisque les faisceaux constants le sont et que cette propriété est stable par image directe et twist à la Tate), on peut donc tester les isomorphismes ci-dessus fibre à fibre. Les tiges du faisceau
![]() $R^q\psi _* \mu _n$
se calculent grâce au théorème de changement de base [Reference de Jong and van der Put9, TH 3.7.3] et font intervenir la cohomologie du faisceau
$R^q\psi _* \mu _n$
se calculent grâce au théorème de changement de base [Reference de Jong and van der Put9, TH 3.7.3] et font intervenir la cohomologie du faisceau
![]() $\mu _n$
sur les fibres de
$\mu _n$
sur les fibres de
![]() $\psi $
. Ces fibres sont des couronnes de dimension
$\psi $
. Ces fibres sont des couronnes de dimension
![]() $1$
(sur le corps de définition du point considéré), et on a déjà vu le calcul de ces groupes de cohomologie, ce qui permet de conclure.
$1$
(sur le corps de définition du point considéré), et on a déjà vu le calcul de ces groupes de cohomologie, ce qui permet de conclure.
Pour le cas semi-ouvert, on peut trouver un recouvrement croissant de X par des tores monômiaux fermés
![]() $X_k$
. Pour
$X_k$
. Pour
![]() $\varphi _k :X_k \times S\to S$
la projection sur le second facteur, on a d’après la discussion précédente un système projectif constant de complexe
$\varphi _k :X_k \times S\to S$
la projection sur le second facteur, on a d’après la discussion précédente un système projectif constant de complexe
![]() $(\operatorname {\mathrm {R}}\varphi _{k,*}\mu _n)_k$
et on en déduit le calcul de
$(\operatorname {\mathrm {R}}\varphi _{k,*}\mu _n)_k$
et on en déduit le calcul de
![]() $\operatorname {\mathrm {R}}\varphi _{*}\mu _n$
du cas fermé.
$\operatorname {\mathrm {R}}\varphi _{*}\mu _n$
du cas fermé.
Remarque 5.7. Si X est un tore monômial sur un corps complet
![]() $S=\operatorname {\mathrm {Sp}}(L)$
et une couronne Y qui le contient, alors, en reprenant le raisonnement par récurrence précédent sur Y, on montre la bijectivité du morphisme naturel de restriction
$S=\operatorname {\mathrm {Sp}}(L)$
et une couronne Y qui le contient, alors, en reprenant le raisonnement par récurrence précédent sur Y, on montre la bijectivité du morphisme naturel de restriction
![]() $\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(Y,\mu _n)\stackrel {\sim }{\rightarrow }\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X,\mu _n) $
. Par suite exacte de Kummer sur Y (voir [Reference Van der Put31, th. 3.25] pour l’annulation du groupe de Picard de Y et [Reference Junger25, Lemme 4.4.] pour le calcul des fonctions inversibles),
$\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(Y,\mu _n)\stackrel {\sim }{\rightarrow }\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(X,\mu _n) $
. Par suite exacte de Kummer sur Y (voir [Reference Van der Put31, th. 3.25] pour l’annulation du groupe de Picard de Y et [Reference Junger25, Lemme 4.4.] pour le calcul des fonctions inversibles),
En particulier, tout revêtement étale de groupe de Galois
![]() $\mu _n$
de
$\mu _n$
de
![]() $X_L$
est un revêtement de Kummer de la forme
$X_L$
est un revêtement de Kummer de la forme
![]() $X((\lambda x^\beta )^{1/n})$
pour
$X((\lambda x^\beta )^{1/n})$
pour
![]() $\beta $
dans
$\beta $
dans
![]() ${\mathbb {Z}}^d$
et
${\mathbb {Z}}^d$
et
![]() $\lambda $
dans
$\lambda $
dans
![]() $L^{*}$
.
$L^{*}$
.
5.4 Cohomologie de de Rham d’un revêtement cyclique modéré d’un tore monomial
Le but de ce paragraphe est de calculer la cohomologie de de Rham d’un revêtement cyclique
![]() ${\mathcal {T}} = X((\lambda x^\beta )^{1/n})$
(avec
${\mathcal {T}} = X((\lambda x^\beta )^{1/n})$
(avec
![]() $\beta \in {\mathbb {Z}}^d$
et
$\beta \in {\mathbb {Z}}^d$
et
![]() $\lambda \in L^{*}$
) d’un tore monômial
$\lambda \in L^{*}$
) d’un tore monômial
Posons
 $$ \begin{align*}\pi_0 =\mathrm{PGCD}(n,\beta_1, \cdots, \beta_d), \, \tilde{n}=\frac{n}{\pi_0}, \, \tilde{\beta}=\frac{\beta}{\pi_0}, \, t_0=\frac{t^{\tilde{n}}}{x^{\tilde{\beta}}}.\end{align*} $$
$$ \begin{align*}\pi_0 =\mathrm{PGCD}(n,\beta_1, \cdots, \beta_d), \, \tilde{n}=\frac{n}{\pi_0}, \, \tilde{\beta}=\frac{\beta}{\pi_0}, \, t_0=\frac{t^{\tilde{n}}}{x^{\tilde{\beta}}}.\end{align*} $$
Théorème 5.8. On dispose d’isomorphismes naturels

et
 $$ \begin{align*}\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}})\cong\bigoplus\limits_{{\substack{i=0}}}^{\pi_0 -1}{t_0^i\mathrm{H}^{q}_{\mathrm{dR}}(X)}.\end{align*} $$
$$ \begin{align*}\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}})\cong\bigoplus\limits_{{\substack{i=0}}}^{\pi_0 -1}{t_0^i\mathrm{H}^{q}_{\mathrm{dR}}(X)}.\end{align*} $$
Remarque 5.9. Pour comprendre l’enoncé du théorème, il est intéressant d’étudier le cas analytique complexe. Si l’on prend un espace X de
![]() ${\mathbb {C}}^d$
défini par les mêmes inégalités qu’un tore monômial (i.e.
${\mathbb {C}}^d$
défini par les mêmes inégalités qu’un tore monômial (i.e.
alors X a le type d'homotopie d'un tore.
La cohomologie de de Rham est donc donnée par Künneth:
 $$\begin{align*}\mathrm{H}^{q}_{\mathrm{dR}}(X)=\underset{|I|=q}{\bigoplus} {\mathbb{C}} \cdot d\log( x_I). \end{align*}$$
$$\begin{align*}\mathrm{H}^{q}_{\mathrm{dR}}(X)=\underset{|I|=q}{\bigoplus} {\mathbb{C}} \cdot d\log( x_I). \end{align*}$$
D’après la correspondance de Galois entre les revêtements et les sous-groupes de
![]() $\pi _1(X)$
, un revêtement cyclique
$\pi _1(X)$
, un revêtement cyclique
![]() ${\mathcal {T}}$
de X a le type d’homotopie d’une union disjointe de tores. Cette union s’écrit:
${\mathcal {T}}$
de X a le type d’homotopie d’une union disjointe de tores. Cette union s’écrit:
Le nombre de composantes connexes est la constante
![]() $\pi _0$
introduite dans l’énoncé du théorème. Comme
$\pi _0$
introduite dans l’énoncé du théorème. Comme
![]() $t_0^{\pi _0}=1$
, la famille
$t_0^{\pi _0}=1$
, la famille
![]() $\{t_0^i\}_i$
engendre le même
$\{t_0^i\}_i$
engendre le même
![]() ${\mathbb {C}}$
-espace vectoriel que l’ensemble des idempotents pour les différentes composantes connexes, et on obtient
${\mathbb {C}}$
-espace vectoriel que l’ensemble des idempotents pour les différentes composantes connexes, et on obtient
Avant de passer à la preuve, mentionnons quelques conséquences utiles:
Corollaire 5.10. On reprend les notations précédentes et on se donne un autre tore monômial
![]() $X'$
inclus dans X. Si
$X'$
inclus dans X. Si
![]() ${\mathcal {T}}'$
est la restriction de
${\mathcal {T}}'$
est la restriction de
![]() ${\mathcal {T}}$
à
${\mathcal {T}}$
à
![]() $X'$
(i.e.,
$X'$
(i.e.,
![]() ${\mathcal {T}}' ={\mathcal {T}}\times _X X'$
), alors la flèche de restriction
${\mathcal {T}}' ={\mathcal {T}}\times _X X'$
), alors la flèche de restriction
![]() $\mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}})\rightarrow \mathrm {H}^{*}_{\mathrm {dR}} ({{\mathcal {T}}'})$
est un isomorphisme qui respecte la décomposition en parties isotypiques.
$\mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}})\rightarrow \mathrm {H}^{*}_{\mathrm {dR}} ({{\mathcal {T}}'})$
est un isomorphisme qui respecte la décomposition en parties isotypiques.
Démonstration. La base explicite du théorème 5.8 est conservée par la restriction
![]() $\Omega _{{\mathcal {T}}^\dagger /L}^q \to \Omega _{({\mathcal {T}}')^\dagger /L}^q$
d’où la bijectivité. Pour l’assertion sur les parties isotypiques, l’inclusion induit une application
$\Omega _{{\mathcal {T}}^\dagger /L}^q \to \Omega _{({\mathcal {T}}')^\dagger /L}^q$
d’où la bijectivité. Pour l’assertion sur les parties isotypiques, l’inclusion induit une application
![]() $\mu _n$
-équivariante entre les complexes de de Rham et le résultat s’en déduit. Pour un argument plus explicite, on a la décomposition en espaces propres
$\mu _n$
-équivariante entre les complexes de de Rham et le résultat s’en déduit. Pour un argument plus explicite, on a la décomposition en espaces propres
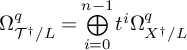 $\Omega ^q_{{\mathcal {T}}^\dagger /L}=\bigoplus \limits _{{\substack {i=0}}}^{n-1}{t^i \Omega ^q_{X^\dagger /L}}$
et pour i fixé chaque
$\Omega ^q_{{\mathcal {T}}^\dagger /L}=\bigoplus \limits _{{\substack {i=0}}}^{n-1}{t^i \Omega ^q_{X^\dagger /L}}$
et pour i fixé chaque
![]() $t_0^i\mathrm {H}^{q}_{\mathrm {dR}}(X)$
est un espace propre de
$t_0^i\mathrm {H}^{q}_{\mathrm {dR}}(X)$
est un espace propre de
![]() $\mathrm {H}^{q}_{\mathrm {dR}} ({\mathcal {T}})$
.
$\mathrm {H}^{q}_{\mathrm {dR}} ({\mathcal {T}})$
.
Corollaire 5.11. Les conclusions de 5.8 et 5.10 sont encore vraies quand X est un tore monômial semi-ouvert.
Démonstration. On écrit
![]() $X=\bigcup _i X_i$
comme une réunion croissante de tores monômiaux. On a alors
$X=\bigcup _i X_i$
comme une réunion croissante de tores monômiaux. On a alors
![]() ${\mathcal {T}}=\bigcup _i {\mathcal {T}}\times _X X_i = \bigcup _i {\mathcal {T}}_i$
. Fixons
${\mathcal {T}}=\bigcup _i {\mathcal {T}}\times _X X_i = \bigcup _i {\mathcal {T}}_i$
. Fixons
![]() $i_0\in {\mathbb {N}}$
, d’après ce qui précède, on a
$i_0\in {\mathbb {N}}$
, d’après ce qui précède, on a
d’où
![]() $\mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}})[\chi ]\cong \mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}}_{i_0})[\chi ]$
.
$\mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}})[\chi ]\cong \mathrm {H}^{*}_{\mathrm {dR}} ({\mathcal {T}}_{i_0})[\chi ]$
.
Passons à la preuve de 5.8. Nous commençons par traiter le cas des tores monomiaux (i.e.,
![]() $\pi = \operatorname {\mathrm {Id}}$
et
$\pi = \operatorname {\mathrm {Id}}$
et
![]() ${\mathcal {T}}=X$
). Comme dans la définition, on se donne
${\mathcal {T}}=X$
). Comme dans la définition, on se donne
![]() $r, s, \alpha , \rho , \mu $
définissant X et on choisit des constantes
$r, s, \alpha , \rho , \mu $
définissant X et on choisit des constantes
![]() $u=(u_i)_i$
,
$u=(u_i)_i$
,
![]() $v=(v_i)_i$
et
$v=(v_i)_i$
et
![]() $w_1$
,
$w_1$
,
![]() $w_2$
dans L telles que
$w_2$
dans L telles que
Si
![]() $x=(x_i)_i$
désigne la variable sur X, alors
$x=(x_i)_i$
désigne la variable sur X, alors
En particulier, toute fonction f appartient à
![]() ${\mathscr {O}}(X^{\dagger })$
admet un développement unique
${\mathscr {O}}(X^{\dagger })$
admet un développement unique
![]() $f= \sum _{\nu \in {\mathbb {Z}}^d} a_{\nu } x^{\nu }$
. Nous aurons besoin du résultat technique suivant:
$f= \sum _{\nu \in {\mathbb {Z}}^d} a_{\nu } x^{\nu }$
. Nous aurons besoin du résultat technique suivant:
Lemme 5.12 (Intégration).
Pour
![]() $i \le d$
et
$i \le d$
et
![]() $f= \sum _{\nu \in {\mathbb {Z}}^d} a_{\nu } x^{\nu } \in {\mathscr {O}}(X^{\dagger })$
, il existe une section surconvergente de développement
$f= \sum _{\nu \in {\mathbb {Z}}^d} a_{\nu } x^{\nu } \in {\mathscr {O}}(X^{\dagger })$
, il existe une section surconvergente de développement
![]() $\sum _{\nu \in {\mathbb {Z}}^d :\nu _i\neq 0} \frac {1}{\nu _i} a_{\nu } x^{\nu } \in {\mathscr {O}}(X^{\dagger })$
.
$\sum _{\nu \in {\mathbb {Z}}^d :\nu _i\neq 0} \frac {1}{\nu _i} a_{\nu } x^{\nu } \in {\mathscr {O}}(X^{\dagger })$
.
Démonstration. Réécrivons f sous la forme
 $$\begin{align*}\sum_{ (\beta, \gamma, \delta_1, \delta_2) \in {\mathbb{N}}^d \times {\mathbb{N}}^d \times {\mathbb{N}} \times {\mathbb{N}}} m_{\beta, \gamma, \delta_1, \delta_2} (\frac{x}{u})^{\beta} (\frac{v}{x})^{\gamma} (\frac{x^{\alpha}}{w_1})^{\delta_1} (\frac{w_2}{x^{\alpha}})^{\delta_2} \end{align*}$$
$$\begin{align*}\sum_{ (\beta, \gamma, \delta_1, \delta_2) \in {\mathbb{N}}^d \times {\mathbb{N}}^d \times {\mathbb{N}} \times {\mathbb{N}}} m_{\beta, \gamma, \delta_1, \delta_2} (\frac{x}{u})^{\beta} (\frac{v}{x})^{\gamma} (\frac{x^{\alpha}}{w_1})^{\delta_1} (\frac{w_2}{x^{\alpha}})^{\delta_2} \end{align*}$$
tel qu'il existe
![]() $h>1$
tel que
$h>1$
tel que
![]() $h^{e(\beta , \gamma , \delta _1, \delta _2)} | m_{\beta , \gamma , \delta _1, \delta _2} | \to 0$
avec
$h^{e(\beta , \gamma , \delta _1, \delta _2)} | m_{\beta , \gamma , \delta _1, \delta _2} | \to 0$
avec
![]() $e(\beta , \gamma , \delta _1, \delta _2)= \sum _{1 \le k \le d} \beta _k + \sum _{1 \le k \le d} \gamma _k + \delta _1 + \delta _2$
. Nous voulons montrer que le développement suivant définit bien une section surconvergente:
$e(\beta , \gamma , \delta _1, \delta _2)= \sum _{1 \le k \le d} \beta _k + \sum _{1 \le k \le d} \gamma _k + \delta _1 + \delta _2$
. Nous voulons montrer que le développement suivant définit bien une section surconvergente:
 $$\begin{align*}\sum_{ (\beta, \gamma, \delta_1, \delta_2) } \frac{m_{\beta, \gamma, \delta_1, \delta_2}}{\beta_i - \gamma_i + \alpha_i(\delta_1- \delta_2)} (\frac{x}{u})^{\beta} (\frac{v}{x})^{\gamma} (\frac{x^{\alpha}}{w_1})^{\delta_1} (\frac{w_2}{x^{\alpha}})^{\delta_2}\end{align*}$$
$$\begin{align*}\sum_{ (\beta, \gamma, \delta_1, \delta_2) } \frac{m_{\beta, \gamma, \delta_1, \delta_2}}{\beta_i - \gamma_i + \alpha_i(\delta_1- \delta_2)} (\frac{x}{u})^{\beta} (\frac{v}{x})^{\gamma} (\frac{x^{\alpha}}{w_1})^{\delta_1} (\frac{w_2}{x^{\alpha}})^{\delta_2}\end{align*}$$
où
![]() $(\beta , \gamma , \delta _1, \delta _2)$
parcourt les termes tels que
$(\beta , \gamma , \delta _1, \delta _2)$
parcourt les termes tels que
![]() $\beta _i - \gamma _i + \alpha _i(\delta _1- \delta _2)\neq 0$
.
$\beta _i - \gamma _i + \alpha _i(\delta _1- \delta _2)\neq 0$
.
Pour tout
![]() $h_1 \in ] 1, h[$
, on a
$h_1 \in ] 1, h[$
, on a
![]() $(\frac {h_1}{h})^{e(\beta , \gamma , \delta _1, \delta _2)} | \frac {1}{ \beta _i - \gamma _i + \alpha _i (\delta _1- \delta _2)} | \to 0$
pour le filtre des parties finies et donc
$(\frac {h_1}{h})^{e(\beta , \gamma , \delta _1, \delta _2)} | \frac {1}{ \beta _i - \gamma _i + \alpha _i (\delta _1- \delta _2)} | \to 0$
pour le filtre des parties finies et donc
 $$\begin{align*}h_1^{e(\beta, \gamma, \delta_1, \delta_2)} | \frac{m_{\beta, \gamma, \delta_1, \delta_2}}{\beta_i - \gamma_i + \alpha_i(\delta_1- \delta_2)} | = h^{e(\beta, \gamma, \delta_1, \delta_2)} | m_{\beta, \gamma, \delta_1, \delta_2} | \frac{(h_1/h)^{e(\beta, \gamma, \delta_1, \delta_2)}}{| \beta_i- \gamma_i+ \alpha_i(\delta_1- \delta_2)| } \to 0 \end{align*}$$
$$\begin{align*}h_1^{e(\beta, \gamma, \delta_1, \delta_2)} | \frac{m_{\beta, \gamma, \delta_1, \delta_2}}{\beta_i - \gamma_i + \alpha_i(\delta_1- \delta_2)} | = h^{e(\beta, \gamma, \delta_1, \delta_2)} | m_{\beta, \gamma, \delta_1, \delta_2} | \frac{(h_1/h)^{e(\beta, \gamma, \delta_1, \delta_2)}}{| \beta_i- \gamma_i+ \alpha_i(\delta_1- \delta_2)| } \to 0 \end{align*}$$
et on obtient bien une section surconvergente sur X de développement
![]() $\sum _{\nu :\nu _i\neq 0} \frac {1}{\nu _i} a_{\nu } x^\nu $
.
$\sum _{\nu :\nu _i\neq 0} \frac {1}{\nu _i} a_{\nu } x^\nu $
.
Une q-forme surconvergente admet un unique développement ![]() . Nous dirons que
. Nous dirons que
![]() $\omega $
contient un terme en
$\omega $
contient un terme en
![]() $x_i$
(resp. un terme en
$x_i$
(resp. un terme en
![]() $d\log (x_i)$
) s’il existe
$d\log (x_i)$
) s’il existe
![]() $a_{\nu , I} \neq 0$
avec
$a_{\nu , I} \neq 0$
avec
![]() $\nu _i \neq 0$
(resp. avec
$\nu _i \neq 0$
(resp. avec
![]() $i \in I$
). On appelle
$i \in I$
). On appelle
![]() $\Omega ^q_{X^{\dagger }/L} [r] $
le sous-module des formes qui ne contiennent aucun terme en
$\Omega ^q_{X^{\dagger }/L} [r] $
le sous-module des formes qui ne contiennent aucun terme en
![]() $x_i$
ou
$x_i$
ou
![]() $d \log (x_i)$
pour
$d \log (x_i)$
pour
![]() $i>r$
. On observe l’inclusion
$i>r$
. On observe l’inclusion
![]() $d(\Omega ^q_{X^{\dagger }/L} [r] ) \subset \Omega ^{q+1}_{X^{\dagger }/L} [r] $
.
$d(\Omega ^q_{X^{\dagger }/L} [r] ) \subset \Omega ^{q+1}_{X^{\dagger }/L} [r] $
.
On impose l’ordre lexicographique sur les couples
![]() $(q,r)$
et on montre par récurrence sur
$(q,r)$
et on montre par récurrence sur
![]() $(q,r)$
l’égalité suivante:Footnote
6
$(q,r)$
l’égalité suivante:Footnote
6

Il est aisé de voir que les modules apparaissant dans le terme de droite sont en somme directe et nous laissons la vérification de ce fait au lecteur. Nous allons seulement prouver que ces modules engendrent bien le sous-ensemble des q-formes fermées.
Si
![]() $q=0$
, comme X est géométriquement connexe, on a
$q=0$
, comme X est géométriquement connexe, on a
![]() $\mathrm {H}^{0}_{\mathrm {dR}}(X)= L= L \cdot d\log (x_{\emptyset })$
.
$\mathrm {H}^{0}_{\mathrm {dR}}(X)= L= L \cdot d\log (x_{\emptyset })$
.
Soit
![]() $q \ge 1$
, supposons le résultat vrai pour tout
$q \ge 1$
, supposons le résultat vrai pour tout
![]() $(q',r') < (q,r)$
. Si
$(q',r') < (q,r)$
. Si
![]() $\omega \in (\Omega ^q_{X^{\dagger }/L}[r])^{d=0}$
, elle se décompose de manière unique de la formeFootnote
7
$\omega \in (\Omega ^q_{X^{\dagger }/L}[r])^{d=0}$
, elle se décompose de manière unique de la formeFootnote
7
 $$\begin{align*}\omega = \sum_{j \in {\mathbb{Z}}} x_r^j \omega_j^{(0)}+ \sum_{j \in {\mathbb{Z}}} x_r^j \omega_j^{(1)} \wedge d\log(x_r) \end{align*}$$
$$\begin{align*}\omega = \sum_{j \in {\mathbb{Z}}} x_r^j \omega_j^{(0)}+ \sum_{j \in {\mathbb{Z}}} x_r^j \omega_j^{(1)} \wedge d\log(x_r) \end{align*}$$
avec
![]() $\omega _j^{(i)} \in \Omega ^{q-i}_{X^{\dagger }/L}[r-1]$
. Par fermeture de
$\omega _j^{(i)} \in \Omega ^{q-i}_{X^{\dagger }/L}[r-1]$
. Par fermeture de
![]() $\omega $
,
$\omega $
,
 $$ \begin{align} d\omega= \sum_{j \in {\mathbb{Z}}} x_r^j d \omega_j^{(0)} + \sum_{j \in {\mathbb{Z}}} x_r^j ((-1)^q j\omega_j^{(0)} + d \omega_j^{(1)}) \wedge d \log(x_r) =0 \end{align} $$
$$ \begin{align} d\omega= \sum_{j \in {\mathbb{Z}}} x_r^j d \omega_j^{(0)} + \sum_{j \in {\mathbb{Z}}} x_r^j ((-1)^q j\omega_j^{(0)} + d \omega_j^{(1)}) \wedge d \log(x_r) =0 \end{align} $$
d’où
![]() $d\omega _j^{(0)} =0$
et
$d\omega _j^{(0)} =0$
et
![]() $d\omega _j^{(1)}= (-1)^{q-1} j \omega _j^{(0)}$
toujours par unicité de la décomposition. En particulier,
$d\omega _j^{(1)}= (-1)^{q-1} j \omega _j^{(0)}$
toujours par unicité de la décomposition. En particulier,
![]() $d\omega _0^{(1)}=d\omega _0^{(0)}=0$
.
$d\omega _0^{(1)}=d\omega _0^{(0)}=0$
.
D’après 5.12, la somme suivante est une
![]() $(q-1)$
-forme surconvergente de X,
$(q-1)$
-forme surconvergente de X,
 $$\begin{align*}\eta= \sum_{j \neq 0} (-1)^{q-1} \frac{1}{j} x_r^j \omega_j^{(1)}. \end{align*}$$
$$\begin{align*}\eta= \sum_{j \neq 0} (-1)^{q-1} \frac{1}{j} x_r^j \omega_j^{(1)}. \end{align*}$$
On vérifie par calcul direct,
![]() $\omega - d\eta = \omega _0^{(0)} + \omega _0^{(1)} \wedge d\log (x_r)$
(d’après (2)). On a montré que les formes
$\omega - d\eta = \omega _0^{(0)} + \omega _0^{(1)} \wedge d\log (x_r)$
(d’après (2)). On a montré que les formes
![]() $\omega _0^{(0)}$
et
$\omega _0^{(0)}$
et
![]() $\omega _0^{(1)}$
étaient fermés. On peut leur appliquer l’hypothèse de récurrence, ce qui permet de conclure.
$\omega _0^{(1)}$
étaient fermés. On peut leur appliquer l’hypothèse de récurrence, ce qui permet de conclure.
On s’intéresse maintenant au cas général. Nous cherchons à calculer la cohomologie d’un revêtement sur X de la forme
Quitte à étendre L, on suppose qu’il contient les racines
![]() $\pi _0$
-ièmes de l’unité et que
$\pi _0$
-ièmes de l’unité et que
![]() $\lambda $
vaut
$\lambda $
vaut
![]() $1$
. On a alors une décomposition
$1$
. On a alors une décomposition
 $$\begin{align*}{\mathcal{T}}= \coprod_{\zeta \in \mu_{\pi_0}(L)} X((\lambda x^{\tilde{\beta}})^{1/\tilde{n}}):= \coprod_{\zeta \in \mu_{\pi_0}(L)} {\mathcal{T}}_{\zeta}. \end{align*}$$
$$\begin{align*}{\mathcal{T}}= \coprod_{\zeta \in \mu_{\pi_0}(L)} X((\lambda x^{\tilde{\beta}})^{1/\tilde{n}}):= \coprod_{\zeta \in \mu_{\pi_0}(L)} {\mathcal{T}}_{\zeta}. \end{align*}$$
Appelons
![]() ${\mathscr {L}}_{\zeta }$
le polynôme interpolateur de Lagrange s’annulant sur
${\mathscr {L}}_{\zeta }$
le polynôme interpolateur de Lagrange s’annulant sur
![]() $\mu _{\pi _0}(L) \setminus \{ \zeta \}$
et valant
$\mu _{\pi _0}(L) \setminus \{ \zeta \}$
et valant
![]() $1$
en
$1$
en
![]() $\zeta $
. Prenons
$\zeta $
. Prenons
![]() $t \in {\mathscr {O}}^{*}({\mathcal {T}})$
une racine n-ième de
$t \in {\mathscr {O}}^{*}({\mathcal {T}})$
une racine n-ième de
![]() $x^{\beta }$
et
$x^{\beta }$
et
![]() $t_0= \frac {t^{\tilde {n}}}{x^{\tilde {\beta }}}$
. Alors
$t_0= \frac {t^{\tilde {n}}}{x^{\tilde {\beta }}}$
. Alors
![]() ${\mathscr {L}}_{\zeta }(t_0)$
est l’idempotent associé à
${\mathscr {L}}_{\zeta }(t_0)$
est l’idempotent associé à
![]() ${\mathcal {T}}_{\zeta }$
. Supposons que
${\mathcal {T}}_{\zeta }$
. Supposons que
![]() ${\mathcal {T}}_{\zeta } \to X$
induise un isomorphisme
${\mathcal {T}}_{\zeta } \to X$
induise un isomorphisme
![]() $\mathrm {H}^{*}_{\mathrm {dR}}(X) \cong \mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}}_{\zeta })$
, on obtient une suite d’isomorphismes
$\mathrm {H}^{*}_{\mathrm {dR}}(X) \cong \mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}}_{\zeta })$
, on obtient une suite d’isomorphismes
 $$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}}({\mathcal{T}}) = \bigoplus_{\zeta} {\mathscr{L}}_{\zeta}(t_0) \mathrm{H}^{*}_{\mathrm{ dR}}({\mathcal{T}}_{\zeta}) \cong \sum_{j=0}^{\pi_0-1} t_0^j \mathrm{H}^{*}_{\mathrm{dR}}(X) \end{align*}$$
$$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}}({\mathcal{T}}) = \bigoplus_{\zeta} {\mathscr{L}}_{\zeta}(t_0) \mathrm{H}^{*}_{\mathrm{ dR}}({\mathcal{T}}_{\zeta}) \cong \sum_{j=0}^{\pi_0-1} t_0^j \mathrm{H}^{*}_{\mathrm{dR}}(X) \end{align*}$$
car
![]() $\{ t_0^j \}_j$
et
$\{ t_0^j \}_j$
et
![]() $\{ {\mathscr {L}}_{\zeta }(t_0) \}_{\zeta }$
engendrent le même L-espace vectoriel. Il suffit ainsi de raisonner sur chaque
$\{ {\mathscr {L}}_{\zeta }(t_0) \}_{\zeta }$
engendrent le même L-espace vectoriel. Il suffit ainsi de raisonner sur chaque
![]() ${\mathcal {T}}_{\zeta }$
(i.e., on peut supposer
${\mathcal {T}}_{\zeta }$
(i.e., on peut supposer
![]() $\pi _0=1$
).
$\pi _0=1$
).
Considérons maintenant le revêtement de groupe de Galois
![]() $\mu _n^d$
suivant:
$\mu _n^d$
suivant:
Les flèches
![]() $((x_1, \dots , x_d), t_1, \dots , t_d) \mapsto (t_1, \dots , t_d)$
et
$((x_1, \dots , x_d), t_1, \dots , t_d) \mapsto (t_1, \dots , t_d)$
et
![]() $(t_1, \dots , t_d) \mapsto ((t_1^n , t_2^n,\dots , t_d^n), t_1, \dots , t_d)$
induisent une bijection
$(t_1, \dots , t_d) \mapsto ((t_1^n , t_2^n,\dots , t_d^n), t_1, \dots , t_d)$
induisent une bijection
On en déduit la suite d’égalités:
 $$\begin{align*}\mathrm{H}^{i}_{\mathrm{dR}}(\tilde{{\mathcal{T}}})= \bigoplus_{|I|= i } L d\log(t_I) = \bigoplus_{|I|=i} L d\log(x_I) = \mathrm{H}^{i}_{\mathrm{dR}}(X). \end{align*}$$
$$\begin{align*}\mathrm{H}^{i}_{\mathrm{dR}}(\tilde{{\mathcal{T}}})= \bigoplus_{|I|= i } L d\log(t_I) = \bigoplus_{|I|=i} L d\log(x_I) = \mathrm{H}^{i}_{\mathrm{dR}}(X). \end{align*}$$
On remarque aisément que
![]() $\tilde {{\mathcal {T}}}$
est un revêtement de
$\tilde {{\mathcal {T}}}$
est un revêtement de
![]() ${\mathcal {T}}$
de groupe de Galois abélien
${\mathcal {T}}$
de groupe de Galois abélien
![]() $\operatorname {\mathrm {Fix}}_{\mu _n^d}({\mathcal {T}})=\{(\gamma _i)_i\in \mu _n^d : \sum _i \gamma _i\beta _i=0\}$
. La flèche naturelle
$\operatorname {\mathrm {Fix}}_{\mu _n^d}({\mathcal {T}})=\{(\gamma _i)_i\in \mu _n^d : \sum _i \gamma _i\beta _i=0\}$
. La flèche naturelle
![]() $\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}}) \to \mathrm {H}^{*}_{\mathrm {dR}}(\tilde {{\mathcal {T}}})$
identifie
$\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}}) \to \mathrm {H}^{*}_{\mathrm {dR}}(\tilde {{\mathcal {T}}})$
identifie
![]() $\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}})$
à
$\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}})$
à
![]() $\mathrm {H}^{*}_{\mathrm {dR}}(\tilde {{\mathcal {T}}})^{\operatorname {\mathrm {Fix}}_{\mu _n^d}({\mathcal {T}})}$
et est donc injective. On obtient un diagramme commutatif:
$\mathrm {H}^{*}_{\mathrm {dR}}(\tilde {{\mathcal {T}}})^{\operatorname {\mathrm {Fix}}_{\mu _n^d}({\mathcal {T}})}$
et est donc injective. On obtient un diagramme commutatif:

Ainsi,
![]() $\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}}) \cong \mathrm {H}^{*}_{\mathrm {dR}}(X)$
.
$\mathrm {H}^{*}_{\mathrm {dR}}({\mathcal {T}}) \cong \mathrm {H}^{*}_{\mathrm {dR}}(X)$
.
5.5 Une première réduction
Revenons maintenant au contexte du théorème 5.1. En particulier, on dispose du schéma formel
![]() ${\mathcal {X}}$
semi-stable généralisé, d’un revêtement cyclique
${\mathcal {X}}$
semi-stable généralisé, d’un revêtement cyclique
![]() $\pi : {\mathcal {T}}\to {\mathcal {X}}_\eta $
d’ordre premier à p et on note
$\pi : {\mathcal {T}}\to {\mathcal {X}}_\eta $
d’ordre premier à p et on note
![]() $(Y_i)_{i\in I}$
les composantes irréductibles de sa fibre spéciale. Rappelons que l’on note
$(Y_i)_{i\in I}$
les composantes irréductibles de sa fibre spéciale. Rappelons que l’on note
![]() $Y_J=\bigcap _{j\in J} Y_j$
pour
$Y_J=\bigcap _{j\in J} Y_j$
pour
![]() $J\subset I$
. Notons que les deux résultats qui vont suivre seront valables dans les deux cas considérés dans 5.1. Nous spécialiserons au cas
$J\subset I$
. Notons que les deux résultats qui vont suivre seront valables dans les deux cas considérés dans 5.1. Nous spécialiserons au cas
![]() $\pi =\mathrm {Id}$
ou au cas
$\pi =\mathrm {Id}$
ou au cas
![]() ${\mathcal {X}}$
semi-stable (non généralisé) dans la section 5.7.
${\mathcal {X}}$
semi-stable (non généralisé) dans la section 5.7.
Lemme 5.13. Pour démontrer le théorème 5.1 il suffit de prouver la bijectivité de
quand
![]() ${\mathcal {X}}=\operatorname {\mathrm {Spf}} (A)$
est affine formel, connexe et possède un morphisme étale
${\mathcal {X}}=\operatorname {\mathrm {Spf}} (A)$
est affine formel, connexe et possède un morphisme étale
Démonstration. On considère uniquement l’ensemble (fini) des composantes de I qui intersectent J, ce qui nous permet de supposer que I est fini. Pour
![]() $J\subset I$
et
$J\subset I$
et
![]() $M\subset J^c$
, on note
$M\subset J^c$
, on note
(i.e., les points dans toutes les composantes irréductibles de J qui évitent celles de M). Si de plus
![]() $ m$
est un entier positif, on note
$ m$
est un entier positif, on note
 $$ \begin{align*}\mathring{Y}_{J,M}^{m}=\bigcup\limits_{{\substack{N\subset M\\ |N|=m}}}^{}{\mathring{Y}_{J,N}}\end{align*} $$
$$ \begin{align*}\mathring{Y}_{J,M}^{m}=\bigcup\limits_{{\substack{N\subset M\\ |N|=m}}}^{}{\mathring{Y}_{J,N}}\end{align*} $$
(i.e., les points dans toutes les composantes de J qui évitent au moins m composantes dans M). On remarque les égalités
![]() $Y_J = \mathring {Y}_{J,M}^{0}$
et
$Y_J = \mathring {Y}_{J,M}^{0}$
et
![]() $\mathring {Y}_{J,M}^{|M|}=\mathring {Y}_{J,M}$
.
$\mathring {Y}_{J,M}^{|M|}=\mathring {Y}_{J,M}$
.
On raisonne sur la chaîne d’inclusions
il suffit donc de montrer (pour tout m) la bijectivité de la flèche naturelle
Notons que
![]() $\mathring {Y}^1_{J,J^c}=Y_J\backslash Y_I$
. Nous allons construire un schéma formel auxiliaire
$\mathring {Y}^1_{J,J^c}=Y_J\backslash Y_I$
. Nous allons construire un schéma formel auxiliaire
![]() $\tilde {{\mathcal {X}}}$
de réduction semi-stable généralisée pour déduire le cas m quelconque à partir du cas
$\tilde {{\mathcal {X}}}$
de réduction semi-stable généralisée pour déduire le cas m quelconque à partir du cas
![]() $m=0$
.
$m=0$
.
Chaque
![]() $]\mathring {Y}_{J,J^c}^{m}[$
admet par définition un recouvrement admissible par les ouverts suivants
$]\mathring {Y}_{J,J^c}^{m}[$
admet par définition un recouvrement admissible par les ouverts suivants
![]() $(]\mathring {Y}_{J,N}[)_{N\subset J^c : |N|=m}$
. Les intersections finies de ces ouverts vérifientFootnote
8
$(]\mathring {Y}_{J,N}[)_{N\subset J^c : |N|=m}$
. Les intersections finies de ces ouverts vérifientFootnote
8
avec
![]() $M=\bigcup _{N\in Q} N$
. Lorsque Q varie, M parcourt l’ensemble des parties disjointes de J pour tout M de cardinal au moins m. On se ramène donc, grâce à la suite spectrale de Cech, à montrer l’isomorphisme
$M=\bigcup _{N\in Q} N$
. Lorsque Q varie, M parcourt l’ensemble des parties disjointes de J pour tout M de cardinal au moins m. On se ramène donc, grâce à la suite spectrale de Cech, à montrer l’isomorphisme
pour tout M de cardinal au moins m. Quand M n’est pas de cardinal m, on a
![]() $\mathring {Y}_{J,M}=\mathring {Y}_{J,M}\cap \mathring {Y}_{J,J^c}^{m+1}$
et la bijectivité est triviale.
$\mathring {Y}_{J,M}=\mathring {Y}_{J,M}\cap \mathring {Y}_{J,J^c}^{m+1}$
et la bijectivité est triviale.
Quand M est de cardinal m, on se place dans la clôtureFootnote
9
![]() $\tilde {{\mathcal {X}}}$
de
$\tilde {{\mathcal {X}}}$
de
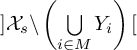 $]{\mathcal {X}}_s\backslash \left (\bigcup \limits _{{\substack {i\in M}}}^{}{Y_i}\right )[$
dans
$]{\mathcal {X}}_s\backslash \left (\bigcup \limits _{{\substack {i\in M}}}^{}{Y_i}\right )[$
dans
![]() $ {\mathcal {X}}$
. Les composantes irréductibles de
$ {\mathcal {X}}$
. Les composantes irréductibles de
![]() $\tilde {{\mathcal {X}}}_s$
sont indexées par
$\tilde {{\mathcal {X}}}_s$
sont indexées par
![]() $I\backslash M$
. On reprend les notations
$I\backslash M$
. On reprend les notations
![]() $\tilde {Y}_J$
,
$\tilde {Y}_J$
,
![]() $\mathring {\tilde {Y}}_{J,N}$
et
$\mathring {\tilde {Y}}_{J,N}$
et
![]() $\mathring {\tilde {Y}}_{J,N}^m$
pour
$\mathring {\tilde {Y}}_{J,N}^m$
pour
![]() $J\subset M^c$
et
$J\subset M^c$
et
![]() $N\subset (M\cup J)^c$
. On observe
$N\subset (M\cup J)^c$
. On observe
On s’est ramené à la condition suffisante du lemme par l’observation
![]() $\tilde {Y}_J\backslash \tilde {Y}_I=\mathring {\tilde {Y}}_{J,J^c}^1$
.
$\tilde {Y}_J\backslash \tilde {Y}_I=\mathring {\tilde {Y}}_{J,J^c}^1$
.
Il reste à expliquer pourquoi on peut supposer
![]() ${\mathcal {X}}$
affine formel. On se donne un recouvrement affine
${\mathcal {X}}$
affine formel. On se donne un recouvrement affine
![]() ${\mathcal {X}}=\bigcup \limits _{{\substack {s\in S}}}^{}{U_s}$
et un jeu de morphismes étales
${\mathcal {X}}=\bigcup \limits _{{\substack {s\in S}}}^{}{U_s}$
et un jeu de morphismes étales
On note
![]() $U_T=\bigcap \limits _{{\substack {t\in T}}}^{}{U_t}$
pour
$U_T=\bigcap \limits _{{\substack {t\in T}}}^{}{U_t}$
pour
![]() $T\subset S$
. On a un recouvrement admissible
$T\subset S$
. On a un recouvrement admissible
![]() ${\mathcal {T}}=\bigcup \limits _{{\substack {s\in S}}}^{}{\pi ^{-1} (U_{s,\eta })}$
donc par une nouvelle application de la suite spectrale de Cech, il suffit de prouver la bijectivité de
${\mathcal {T}}=\bigcup \limits _{{\substack {s\in S}}}^{}{\pi ^{-1} (U_{s,\eta })}$
donc par une nouvelle application de la suite spectrale de Cech, il suffit de prouver la bijectivité de
pour tout
![]() $T\subset S$
. On s’est donc ramené à
$T\subset S$
. On s’est donc ramené à
![]() ${\mathcal {X}}=U_T =\operatorname {\mathrm {Spf}} (A)$
affine formel,
${\mathcal {X}}=U_T =\operatorname {\mathrm {Spf}} (A)$
affine formel,
![]() ${\mathcal {T}}=\pi ^{-1} (U_{T,\eta })$
affinoïde et
${\mathcal {T}}=\pi ^{-1} (U_{T,\eta })$
affinoïde et
![]() $\varphi ={\varphi _s}_{|U_T}: {\mathcal {X}}\to \operatorname {\mathrm {Spf}} ({\mathcal {O}}_L\left \langle x_1,\cdots , x_d\right \rangle /(x_1^{\alpha _1}\cdots x_r^{\alpha _r}-\varpi ))$
pour un certain
$\varphi ={\varphi _s}_{|U_T}: {\mathcal {X}}\to \operatorname {\mathrm {Spf}} ({\mathcal {O}}_L\left \langle x_1,\cdots , x_d\right \rangle /(x_1^{\alpha _1}\cdots x_r^{\alpha _r}-\varpi ))$
pour un certain
![]() $s\in T$
. Quitte à réduire
$s\in T$
. Quitte à réduire
![]() ${\mathcal {X}}$
, on peut supposer qu’il est connexe.
${\mathcal {X}}$
, on peut supposer qu’il est connexe.
5.6 Une deuxième réduction
Nous supposons maintenant que nous sommes dans le contexte du lemme 5.13. En particulier,
![]() ${\mathcal {X}}=\operatorname {\mathrm {Spf}} (A)$
est affine et connexe et possède un morphisme étale
${\mathcal {X}}=\operatorname {\mathrm {Spf}} (A)$
est affine et connexe et possède un morphisme étale
![]() $\varphi : \operatorname {\mathrm {Spf}} (A)\rightarrow \operatorname {\mathrm {Spf}} ({\mathcal {O}}_L \left \langle x_1,\cdots ,x_d\right \rangle /(x_1^{\alpha _1}\cdots x_r^{\alpha _r} -\varpi ))$
. Notons
$\varphi : \operatorname {\mathrm {Spf}} (A)\rightarrow \operatorname {\mathrm {Spf}} ({\mathcal {O}}_L \left \langle x_1,\cdots ,x_d\right \rangle /(x_1^{\alpha _1}\cdots x_r^{\alpha _r} -\varpi ))$
. Notons
![]() $x_i^{*} =\varphi ^{*} (x_i)\in A$
et
$x_i^{*} =\varphi ^{*} (x_i)\in A$
et
![]() $\overline {x}_i$
son image en fibre spéciale. Quitte à réduire
$\overline {x}_i$
son image en fibre spéciale. Quitte à réduire
![]() ${\mathcal {X}}$
, on peut supposer
${\mathcal {X}}$
, on peut supposer ![]() ,
, ![]() ,
,
![]() $Y_i =V(\overline {x}_i)$
. Notons aussi que
$Y_i =V(\overline {x}_i)$
. Notons aussi que
![]() ${\mathcal {T}}$
est affinoide, disons
${\mathcal {T}}$
est affinoide, disons
![]() ${\mathcal {T}}=\operatorname {\mathrm {Sp}}(B)$
.
${\mathcal {T}}=\operatorname {\mathrm {Sp}}(B)$
.
Lemme 5.14. Pour montrer 5.13, il suffit de prouver que pour toute partition ![]() et tous
et tous
![]() $\lambda ,\beta \in ]0,1[\cap |\overline {K}^{*}|$
, les restrictions de
$\lambda ,\beta \in ]0,1[\cap |\overline {K}^{*}|$
, les restrictions de
![]() ${\mathcal {T}}$
à
${\mathcal {T}}$
à
![]() $\tilde {C}$
et à
$\tilde {C}$
et à
![]() $\tilde {C}'$
ont la même cohomologie de de Rham, où
$\tilde {C}'$
ont la même cohomologie de de Rham, où
 $$\begin{align*}\tilde{C}&=\left\lbrace s\in {\mathcal{X}}_\eta : |x_{j_1}^{*} (s)|\leq \lambda, |x_{j_2}^{*} (s)|=\beta, |x_{j_3}^{*} (s)|\leq\beta, \, \forall j_k\in J_k\right\rbrace,\\\tilde{C}'&=\left\lbrace s\in {\mathcal{X}}_\eta : |x_{j_1}^{*} (s)|\leq \lambda, |x_{j_2}^{*} (s)|=\beta, |x_{j_3}^{*} (s)|=\beta, \, \forall j_k\in J_k\right\rbrace.\end{align*}$$
$$\begin{align*}\tilde{C}&=\left\lbrace s\in {\mathcal{X}}_\eta : |x_{j_1}^{*} (s)|\leq \lambda, |x_{j_2}^{*} (s)|=\beta, |x_{j_3}^{*} (s)|\leq\beta, \, \forall j_k\in J_k\right\rbrace,\\\tilde{C}'&=\left\lbrace s\in {\mathcal{X}}_\eta : |x_{j_1}^{*} (s)|\leq \lambda, |x_{j_2}^{*} (s)|=\beta, |x_{j_3}^{*} (s)|=\beta, \, \forall j_k\in J_k\right\rbrace.\end{align*}$$
Démonstration. Rappelons que:
 $$\begin{align*}]Y_J[_{\mathcal{X}}&=\{s\in {\mathcal{X}}_\eta |\, \forall j\in J\,, |x_j^{*}(s)| < 1\},\\]Y_J\backslash Y_I[_{\mathcal{X}}&=\{s\in ]Y_J[_{\mathcal{X}}|\, \exists i\in J^c, |x_i^{*}(s)| = 1\}.\end{align*}$$
$$\begin{align*}]Y_J[_{\mathcal{X}}&=\{s\in {\mathcal{X}}_\eta |\, \forall j\in J\,, |x_j^{*}(s)| < 1\},\\]Y_J\backslash Y_I[_{\mathcal{X}}&=\{s\in ]Y_J[_{\mathcal{X}}|\, \exists i\in J^c, |x_i^{*}(s)| = 1\}.\end{align*}$$
Nous allons filtrer ces espaces par des ouverts plus simples. Pour
![]() $\lambda \in ]0,1[\cap |\overline {K}^{*}|$
posonsFootnote
10
$\lambda \in ]0,1[\cap |\overline {K}^{*}|$
posonsFootnote
10
On définit
![]() $]Y_J\backslash Y_I[_{\mathcal {X}} (\frac {J}{\lambda })$
d’une manière semblable et on remarque que
$]Y_J\backslash Y_I[_{\mathcal {X}} (\frac {J}{\lambda })$
d’une manière semblable et on remarque que
![]() $\pi ^{-1}(]Y_J[_{\mathcal {X}})=\bigcup \limits _{{\substack {\lambda < 1}}}^{}{\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda })})$
est un recouvrement admissible (et la situation est similaire pour
$\pi ^{-1}(]Y_J[_{\mathcal {X}})=\bigcup \limits _{{\substack {\lambda < 1}}}^{}{\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda })})$
est un recouvrement admissible (et la situation est similaire pour
![]() $\pi ^{-1}(]Y_J\backslash Y_I[_{\mathcal {X}})$
). Il suffit donc de montrer la bijectivité de
$\pi ^{-1}(]Y_J\backslash Y_I[_{\mathcal {X}})$
). Il suffit donc de montrer la bijectivité de
pour tout
![]() $\lambda $
comme ci-dessus.
$\lambda $
comme ci-dessus.
Ensuite, intéressons-nous à l’espace
 $$\begin{align*}\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}=\{s\in {\mathcal{X}}_\eta (\frac{J}{\lambda})|\,\exists i\in J^c,\,\, |x_i^{*}(s)|\ge \beta\}\end{align*}$$
$$\begin{align*}\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}=\{s\in {\mathcal{X}}_\eta (\frac{J}{\lambda})|\,\exists i\in J^c,\,\, |x_i^{*}(s)|\ge \beta\}\end{align*}$$
pour
![]() $\beta \in ]0,1[\cap |\overline {K}^{*}|$
. On remarque la suite d’inclusion
$\beta \in ]0,1[\cap |\overline {K}^{*}|$
. On remarque la suite d’inclusion
 $$ \begin{align*}\pi^{-1}(]Y_J\backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda})) \subset \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}) \subset \pi^{-1}({\mathcal{X}}_\eta(\frac{J}{\lambda})).\end{align*} $$
$$ \begin{align*}\pi^{-1}(]Y_J\backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda})) \subset \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}) \subset \pi^{-1}({\mathcal{X}}_\eta(\frac{J}{\lambda})).\end{align*} $$
Étudions d’abord la flèche en cohomologie induite par la première inclusion. On a un recouvrement admissible
![]() $(\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{\left \lbrace i \right \rbrace })))_{i\in J^c}$
de
$(\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{\left \lbrace i \right \rbrace })))_{i\in J^c}$
de
![]() $\pi ^{-1}(\bigcup \limits _{{\substack {i\in J^c}}}^{}{{\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{\left \lbrace i \right \rbrace })})$
et les intersections sont de la forme
$\pi ^{-1}(\bigcup \limits _{{\substack {i\in J^c}}}^{}{{\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{\left \lbrace i \right \rbrace })})$
et les intersections sont de la forme
![]() $\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{M}))$
pour
$\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{M}))$
pour
![]() $M\subset J^c$
.
$M\subset J^c$
.
De plus, on a l’identité
 $$\begin{align*}\pi^{-1}(]Y_J \backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda} ))^\dagger=\bigcap_{\beta < 1}\ \pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{M}))^\dagger\end{align*}$$
$$\begin{align*}\pi^{-1}(]Y_J \backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda} ))^\dagger=\bigcap_{\beta < 1}\ \pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{M}))^\dagger\end{align*}$$
car chaque voisinage stricte de
![]() $\pi ^{-1}(]Y_J \backslash Y_I[_{\mathcal {X}} (\frac {J}{\lambda } ))$
contient un ouvert de la forme
$\pi ^{-1}(]Y_J \backslash Y_I[_{\mathcal {X}} (\frac {J}{\lambda } ))$
contient un ouvert de la forme
![]() $\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{M}))$
pour un certain
$\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{M}))$
pour un certain
![]() $\beta $
. En comparant les complexes de de Rham surconvergeant, on obtient la bijectivité de
$\beta $
. En comparant les complexes de de Rham surconvergeant, on obtient la bijectivité de
 $$\begin{align*}\varinjlim_{\beta < 1}\ \mathrm{H}^{*}_{\mathrm{dR}} ( \pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{M})))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J\backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda})))\end{align*}$$
$$\begin{align*}\varinjlim_{\beta < 1}\ \mathrm{H}^{*}_{\mathrm{dR}} ( \pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{M})))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J\backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda})))\end{align*}$$
puis celle de
 $$\begin{align*}\varinjlim_{\beta < 1}\ \mathrm{H}^{*}_{\mathrm{dR}} ( \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J\backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda})))\end{align*}$$
$$\begin{align*}\varinjlim_{\beta < 1}\ \mathrm{H}^{*}_{\mathrm{dR}} ( \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(]Y_J\backslash Y_I[_{\mathcal{X}} (\frac{J}{\lambda})))\end{align*}$$
grâce à la suite spectrale de Cech.
Il suffit donc d’établir l’isomorphisme suivant pour tout
![]() $\beta $
$\beta $
 $$ \begin{align} \mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda})))\xrightarrow[]{\sim}\mathrm{ H}^{*}_{\mathrm{dR}} ( \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace}}))) \end{align} $$
$$ \begin{align} \mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda})))\xrightarrow[]{\sim}\mathrm{ H}^{*}_{\mathrm{dR}} ( \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace}}))) \end{align} $$
en montrant que cela découle de la condition imposée dans l’énoncé.
On a un recouvrement admissible à deux termes
 $$ \begin{align*}\pi^{-1}({\mathcal{X}}_\eta(\frac{J}{\lambda}))=\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta})) \cup \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta(\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}).\end{align*} $$
$$ \begin{align*}\pi^{-1}({\mathcal{X}}_\eta(\frac{J}{\lambda}))=\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta})) \cup \pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta(\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})}).\end{align*} $$
En utilisant la suite exacte de Mayer-Vietoris qui en découle, il suffit d’établirFootnote 11
 $$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta})))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta}) \cap \bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta(\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})})).\end{align*}$$
$$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta})))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta}) \cap \bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta(\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})})).\end{align*}$$
On réécrit
 $$ \begin{align*}\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta}) \cap \bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})})=\pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace}, \frac{J^c}{\beta}))}).\end{align*} $$
$$ \begin{align*}\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta}) \cap \bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace})})=\pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace}, \frac{J^c}{\beta}))}).\end{align*} $$
Pour établir l’isomorphisme ci-dessus, comparons les deux espaces considérés avec
![]() $\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda }, (\frac {J^c}{\beta })^{\pm 1}))$
ie. prouvons la bijectivité des deux flèches
$\pi ^{-1}({\mathcal {X}}_\eta (\frac {J}{\lambda }, (\frac {J^c}{\beta })^{\pm 1}))$
ie. prouvons la bijectivité des deux flèches
 $$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta})))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, (\frac{J^c}{\beta})^{\pm 1}))),\\\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace}, \frac{J^c}{\beta}))}))\xrightarrow[]{\sim}\mathrm{ H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, (\frac{J^c}{\beta})^{\pm 1}))). \end{align*}$$
$$\begin{align*}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, \frac{J^c}{\beta})))\xrightarrow[]{\sim}\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, (\frac{J^c}{\beta})^{\pm 1}))),\\\mathrm{H}^{*}_{\mathrm{dR}} (\pi^{-1}(\bigcup\limits_{{\substack{i\in J^c}}}^{}{{\mathcal{X}}_\eta (\frac{J}{\lambda},\frac{\beta}{\left\lbrace i \right\rbrace}, \frac{J^c}{\beta}))}))\xrightarrow[]{\sim}\mathrm{ H}^{*}_{\mathrm{dR}} (\pi^{-1}({\mathcal{X}}_\eta (\frac{J}{\lambda}, (\frac{J^c}{\beta})^{\pm 1}))). \end{align*}$$
Pour la première, cela revient à comparer les deux couronnes de l’énoncé du lemme 5.14 pour la partition
![]() $I=J\cup \emptyset \cup J^c$
. D’après la suite spectrale de Cech pour le recouvrement
$I=J\cup \emptyset \cup J^c$
. D’après la suite spectrale de Cech pour le recouvrement
![]() $({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{\left \lbrace i \right \rbrace }, \frac {J^c}{\beta }))_{i\in J^c}$
, on se ramène pour la deuxième à
$({\mathcal {X}}_\eta (\frac {J}{\lambda },\frac {\beta }{\left \lbrace i \right \rbrace }, \frac {J^c}{\beta }))_{i\in J^c}$
, on se ramène pour la deuxième à
pour tout
![]() $M\subset J^c$
. Là encore, cela revient à établir la condition suffisante du lemme pour la partition
$M\subset J^c$
. Là encore, cela revient à établir la condition suffisante du lemme pour la partition
![]() $I=J\cup M\cup (I\backslash (J\cup M))$
$I=J\cup M\cup (I\backslash (J\cup M))$
5.7 Fin de la preuve du théorème 5.1
Fixons une partition ![]() et reprenons les notations introduites dans le lemme 5.14. Dans toute la suite, nous appellerons par abus
et reprenons les notations introduites dans le lemme 5.14. Dans toute la suite, nous appellerons par abus
![]() ${\mathcal {T}}$
le revêtement sur
${\mathcal {T}}$
le revêtement sur
![]() $\tilde {C}$
et
$\tilde {C}$
et
![]() ${\mathcal {T}}'$
celui sur
${\mathcal {T}}'$
celui sur
![]() $\tilde {C}'$
. Nous devons comparer les cohomologies de de Rham de
$\tilde {C}'$
. Nous devons comparer les cohomologies de de Rham de
![]() ${\mathcal {T}}$
et de
${\mathcal {T}}$
et de
![]() ${\mathcal {T}}'$
. Pour cela, on considère les inclusions
${\mathcal {T}}'$
. Pour cela, on considère les inclusions
![]() $\tilde {C}' \to \tilde {C} \to ]Y_I[_{\mathcal {X}} =\left \lbrace s \in {\mathcal {X}}_\eta , \forall i\in I, |x_i^{*}(s)|<1\right \rbrace $
. Nous allons commencer par une description plus simple de
$\tilde {C}' \to \tilde {C} \to ]Y_I[_{\mathcal {X}} =\left \lbrace s \in {\mathcal {X}}_\eta , \forall i\in I, |x_i^{*}(s)|<1\right \rbrace $
. Nous allons commencer par une description plus simple de
![]() $ ]Y_I[_{\mathcal {X}}$
, fournie par:
$ ]Y_I[_{\mathcal {X}}$
, fournie par:
Lemme 5.15. Il existe une
![]() ${\mathcal {O}}_L$
-algèbre
${\mathcal {O}}_L$
-algèbre
![]() $\varpi $
-adiquement complète et formellement lisse
$\varpi $
-adiquement complète et formellement lisse
![]() $\hat {B}$
et un isomorphisme
$\hat {B}$
et un isomorphisme
envoyant
![]() $Z_i$
sur
$Z_i$
sur
![]() $x_i^{*}$
.
$x_i^{*}$
.
Démonstration. Le morphisme étale
![]() ${\mathcal {O}}_L\langle X_1,...,X_d\rangle / (X_1^{\alpha _1}... X_r^{\alpha _r}- \varpi ) \rightarrow A$
induit, en complétant
${\mathcal {O}}_L\langle X_1,...,X_d\rangle / (X_1^{\alpha _1}... X_r^{\alpha _r}- \varpi ) \rightarrow A$
induit, en complétant
![]() $(X_1,...,X_r)$
-adiquement, un morphisme étale
$(X_1,...,X_r)$
-adiquement, un morphisme étale
D’après [Reference Berthelot2, (0.2.7)PROPOSITION],
![]() $]Y_I[_{\mathcal {X}}=\operatorname {\mathrm {Spf}}(\hat {A})^{rig}$
. Considérons le diagramme commutatif suivant,
$]Y_I[_{\mathcal {X}}=\operatorname {\mathrm {Spf}}(\hat {A})^{rig}$
. Considérons le diagramme commutatif suivant,

dans lequel
![]() $\theta $
est la projection modulo
$\theta $
est la projection modulo
![]() $J=(X_1,...,X_r )$
et
$J=(X_1,...,X_r )$
et
Observons que l’inclusion canonique
![]() $\iota : {\mathbb {F}}[X_{r+1},..., X_d]\hookrightarrow R/\varpi $
est une section de
$\iota : {\mathbb {F}}[X_{r+1},..., X_d]\hookrightarrow R/\varpi $
est une section de
![]() $\theta $
. Comme
$\theta $
. Comme
![]() $R\rightarrow \hat {A}$
est étale, la section
$R\rightarrow \hat {A}$
est étale, la section
![]() $\iota $
se relève en une section
$\iota $
se relève en une section
![]() $s: \overline {B}\rightarrow \hat {A}/\varpi $
. En effet,
$s: \overline {B}\rightarrow \hat {A}/\varpi $
. En effet,
![]() $\overline {B}$
est lisse sur
$\overline {B}$
est lisse sur
![]() ${\mathbb {F}}$
car étale sur
${\mathbb {F}}$
car étale sur
![]() ${\mathbb {F}}[X_{r+1},...,X_d]$
par changement de base de
${\mathbb {F}}[X_{r+1},...,X_d]$
par changement de base de
![]() $R/\varpi \to \hat {A}/\varpi $
. Ainsi, le morphisme naturel
$R/\varpi \to \hat {A}/\varpi $
. Ainsi, le morphisme naturel
![]() $\overline {B}\stackrel {\sim }{\rightarrow } \hat {A}/(\varpi \hat {A}+J\hat {A})$
se relève en un morphisme
$\overline {B}\stackrel {\sim }{\rightarrow } \hat {A}/(\varpi \hat {A}+J\hat {A})$
se relève en un morphisme
![]() $\overline {B}\to \hat {A}/\varpi $
car
$\overline {B}\to \hat {A}/\varpi $
car
![]() $\hat {A}/\varpi $
est complet pour la topologie J-adique. Pour vérifier que l’on obtient bien la section recherchée, il suffit de montrer que ce morphisme est compatible à
$\hat {A}/\varpi $
est complet pour la topologie J-adique. Pour vérifier que l’on obtient bien la section recherchée, il suffit de montrer que ce morphisme est compatible à
![]() $\iota $
en le réduisant modulo J ce qui est vrai par construction.
$\iota $
en le réduisant modulo J ce qui est vrai par construction.
Par le théorème d’Elkik [Reference Elkik16, THÉORÈME fin section II p568], on peut relever
![]() $\overline {B}$
en une
$\overline {B}$
en une
![]() ${\mathcal {O}}_K$
-algèbre lisse B. Ainsi, en reprenant les arguments de la construction de s, on voit que
${\mathcal {O}}_K$
-algèbre lisse B. Ainsi, en reprenant les arguments de la construction de s, on voit que
![]() $B \to \hat {A}/ \varpi $
se relève en un morphisme
$B \to \hat {A}/ \varpi $
se relève en un morphisme
![]() $B \rightarrow \hat {A} $
puis en
$B \rightarrow \hat {A} $
puis en
![]() $\hat {B} \rightarrow \hat {A} $
, où
$\hat {B} \rightarrow \hat {A} $
, où
![]() $\hat {B}$
est la complétion
$\hat {B}$
est la complétion
![]() $\varpi $
-adique de B. Le diagramme commutatif
$\varpi $
-adique de B. Le diagramme commutatif

fournit un morphisme ![]() envoyant
envoyant
![]() $Z_i$
sur
$Z_i$
sur
![]() $x_i^{*}$
. Par Nakayama topologique,
$x_i^{*}$
. Par Nakayama topologique,
![]() $\beta $
est un isomorphisme car il l’est modulo
$\beta $
est un isomorphisme car il l’est modulo
![]() $(Z_1,...,Z_r,\varpi )$
par construction. On conclut en passant à la fibre génerique.
$(Z_1,...,Z_r,\varpi )$
par construction. On conclut en passant à la fibre génerique.
Notons
![]() $S=\operatorname {\mathrm {Sp}}(\hat {B} \otimes _{{\mathcal {O}}_L} L)$
et
$S=\operatorname {\mathrm {Sp}}(\hat {B} \otimes _{{\mathcal {O}}_L} L)$
et
![]() $X=\{Z=(Z_1,\cdots , Z_r)\in \mathring {{\mathbb {B}}}^{r}_L :Z^{\alpha }=\varpi \} $
. Le lemme ci-dessus fournit un diagramme commutatif
$X=\{Z=(Z_1,\cdots , Z_r)\in \mathring {{\mathbb {B}}}^{r}_L :Z^{\alpha }=\varpi \} $
. Le lemme ci-dessus fournit un diagramme commutatif

où C et
![]() $C'$
sont les espaces par
$C'$
sont les espaces par
 $$\begin{align*}C&=\left\lbrace s\in X |\, |Z_{j_1} (s)|\leq \lambda, |Z_{j_2} (s)|=\beta, |Z_{j_3} (s)|\leq\beta,\, \forall j_k\in J_k\right\rbrace ,\\C'&=\left\lbrace s\in X|\, |Z_{j_1} (s)|\leq \lambda, |Z_{j_2} (s)|=\beta, |Z_{j_3} (s)|=\beta,\, \forall j_k\in J_k\right\rbrace.\end{align*}$$
$$\begin{align*}C&=\left\lbrace s\in X |\, |Z_{j_1} (s)|\leq \lambda, |Z_{j_2} (s)|=\beta, |Z_{j_3} (s)|\leq\beta,\, \forall j_k\in J_k\right\rbrace ,\\C'&=\left\lbrace s\in X|\, |Z_{j_1} (s)|\leq \lambda, |Z_{j_2} (s)|=\beta, |Z_{j_3} (s)|=\beta,\, \forall j_k\in J_k\right\rbrace.\end{align*}$$
On se place maintenant dans le cas où
![]() ${\mathcal {X}}$
est semi-stable ie.
${\mathcal {X}}$
est semi-stable ie.
![]() $\forall i\in I, \alpha _i=1$
. Alors, en exprimant
$\forall i\in I, \alpha _i=1$
. Alors, en exprimant
![]() $Z_1$
en fonction des variables
$Z_1$
en fonction des variables
![]() $Z_2, \cdots , Z_{r}$
, nous pourrons voir les espaces C,
$Z_2, \cdots , Z_{r}$
, nous pourrons voir les espaces C,
![]() $C'$
comme des tores monomiaux géométriquement connexes. Comme on peut raisonner sur chaque composante de S, on suppose de même S connexe. Enfin, quitte à étendre les scalaires, on suppose le corps de base L complet algébriquement clos.
$C'$
comme des tores monomiaux géométriquement connexes. Comme on peut raisonner sur chaque composante de S, on suppose de même S connexe. Enfin, quitte à étendre les scalaires, on suppose le corps de base L complet algébriquement clos.
Lemme 5.16. Les torseurs
![]() $[{\mathcal {T}}]$
et
$[{\mathcal {T}}]$
et
![]() $[{\mathcal {T}}']$
admettent des décompositions en sommes
$[{\mathcal {T}}']$
admettent des décompositions en sommes
![]() $[{\mathcal {T}}_1\times C]+[S\times {\mathcal {T}}_2]$
et
$[{\mathcal {T}}_1\times C]+[S\times {\mathcal {T}}_2]$
et
![]() $[{\mathcal {T}}_1'\times C']+[S\times {\mathcal {T}}_2']$
où
$[{\mathcal {T}}_1'\times C']+[S\times {\mathcal {T}}_2']$
où
![]() ${\mathcal {T}}_1={\mathcal {T}}_1'$
(resp.
${\mathcal {T}}_1={\mathcal {T}}_1'$
(resp.
![]() ${\mathcal {T}}_2$
,
${\mathcal {T}}_2$
,
![]() ${\mathcal {T}}_2'$
) est un
${\mathcal {T}}_2'$
) est un
![]() $\mu _n$
-torseur sur S (resp. C,
$\mu _n$
-torseur sur S (resp. C,
![]() $C'$
).
$C'$
).
Démonstration. On raisonne sur C, l’argument sera le même pour
![]() $C'$
. Introduisons le diagramme
$C'$
. Introduisons le diagramme

On se donne
![]() $c_0 \in C$
un point géométrique et on note
$c_0 \in C$
un point géométrique et on note
![]() $\iota : c_0 \times S \to C \times S$
. D’après la suite spectrale de Leray, on a une suite exacte:
$\iota : c_0 \times S \to C \times S$
. D’après la suite spectrale de Leray, on a une suite exacte:
Les morphismes induits
![]() $\operatorname {\mathrm {R}}^1 \iota ^{*}$
et
$\operatorname {\mathrm {R}}^1 \iota ^{*}$
et
![]() $\operatorname {\mathrm {R}}^2 \iota ^{*}$
fournissent des inverses à droite de
$\operatorname {\mathrm {R}}^2 \iota ^{*}$
fournissent des inverses à droite de
![]() $\operatorname {\mathrm {R}}^1pr_{1}^{*}$
et
$\operatorname {\mathrm {R}}^1pr_{1}^{*}$
et
![]() $\operatorname {\mathrm {R}}^2 pr_{1}^{*}$
, d’où une suite exacte de faisceaux scindée:
$\operatorname {\mathrm {R}}^2 pr_{1}^{*}$
, d’où une suite exacte de faisceaux scindée:
et une identification
![]() $\varphi _* \operatorname {\mathrm {R}}^1 pr_{1,*}\mu _{n,S \times C} \cong \ker (\operatorname {\mathrm {R}}^1 \iota ^{*})$
.
$\varphi _* \operatorname {\mathrm {R}}^1 pr_{1,*}\mu _{n,S \times C} \cong \ker (\operatorname {\mathrm {R}}^1 \iota ^{*})$
.
Les flèches naturelles compatibles
![]() $\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)\to \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(U\times C, \mu _n)$
induisent un morphisme entre le préfaisceau constant
$\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)\to \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(U\times C, \mu _n)$
induisent un morphisme entre le préfaisceau constant
![]() $\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)|_S$
et le préfaisceau
$\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)|_S$
et le préfaisceau
![]() $U\mapsto \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(U\times C, \mu _n)$
. En passant au faisceau associé, on obtient un morphisme naturel
$U\mapsto \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(U\times C, \mu _n)$
. En passant au faisceau associé, on obtient un morphisme naturel
![]() $\delta :\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)|_S\to \operatorname {\mathrm {R}}^1 pr_{1,*}\mu _{n,S \times C}$
. Le faisceau
$\delta :\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)|_S\to \operatorname {\mathrm {R}}^1 pr_{1,*}\mu _{n,S \times C}$
. Le faisceau
![]() $pr_{1,*} \mu _{n,S \times C}$
est surconvergent en tant qu’image directe d’un faisceau constant (à quelques twists à la Tate près), on a d’après [Reference de Jong and van der Put9, Th. 3.7.3]
$pr_{1,*} \mu _{n,S \times C}$
est surconvergent en tant qu’image directe d’un faisceau constant (à quelques twists à la Tate près), on a d’après [Reference de Jong and van der Put9, Th. 3.7.3]
![]() $(\operatorname {\mathrm {R}}^1 pr_{1,*}\mu _{n,S \times C})_s{\kern-1pt}\cong{\kern-1pt} \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)$
pour tout point
$(\operatorname {\mathrm {R}}^1 pr_{1,*}\mu _{n,S \times C})_s{\kern-1pt}\cong{\kern-1pt} \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)$
pour tout point
![]() $s\in S$
et
$s\in S$
et
![]() $\delta $
est un isomorphisme.
$\delta $
est un isomorphisme.
Comme S et C sont connexes, on a, en prenant les sections globales, une suite exacte scindée
avec
![]() $\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n) \stackrel {\sim }{\rightarrow } \ker (\iota ^{*})$
. Mais, on a un morphisme injectif
$\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n) \stackrel {\sim }{\rightarrow } \ker (\iota ^{*})$
. Mais, on a un morphisme injectif
![]() $\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n) \to \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(S \times C, \mu _n)$
induit par
$\mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n) \to \mathrm {H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(S \times C, \mu _n)$
induit par
![]() $pr_{2}^{*}$
. Il reste à prouver que
$pr_{2}^{*}$
. Il reste à prouver que
![]() $\ker (\iota ^{*})= \mathrm {im}(pr_{2}^{*})$
. Le morphisme
$\ker (\iota ^{*})= \mathrm {im}(pr_{2}^{*})$
. Le morphisme
![]() $pr_2^{*}$
envoie un revêtement
$pr_2^{*}$
envoie un revêtement
![]() ${\mathcal {T}}$
sur
${\mathcal {T}}$
sur
![]() $S \times {\mathcal {T}}$
et
$S \times {\mathcal {T}}$
et
![]() $\iota ^{*}$
envoie
$\iota ^{*}$
envoie
![]() ${\mathcal {T}}'$
sur
${\mathcal {T}}'$
sur
![]() $S \times C$
vers sa restriction à
$S \times C$
vers sa restriction à
![]() $S \times c_0 \cong S$
. Il est aisé de voir que
$S \times c_0 \cong S$
. Il est aisé de voir que
![]() $\iota ^{*} \circ pr_2^{*}=0$
(i.e.,
$\iota ^{*} \circ pr_2^{*}=0$
(i.e.,
![]() $\mathrm { im}(pr_{2}^{*})\subset \ker (\iota ^{*})$
). Mais ces deux groupes ont tous deux pour ordre
$\mathrm { im}(pr_{2}^{*})\subset \ker (\iota ^{*})$
). Mais ces deux groupes ont tous deux pour ordre
![]() $|\mathrm { H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)|<\infty $
(cf 5.6 et 5.7), ils sont donc confondus. On a donc la décomposition
$|\mathrm { H}^{1}_{\acute {\mathrm {e}}\mathrm {t}}(C, \mu _n)|<\infty $
(cf 5.6 et 5.7), ils sont donc confondus. On a donc la décomposition
L’énoncé est une traduction en termes de torseurs de cette égalité.
L’espace
![]() ${\mathcal {T}}_1\times _L{\mathcal {T}}_2$
est un revêtement de
${\mathcal {T}}_1\times _L{\mathcal {T}}_2$
est un revêtement de
![]() ${\mathcal {T}}$
de groupe de Galois
${\mathcal {T}}$
de groupe de Galois
![]() $H=\{(g,g^{-1}) : g\in \mu _n\}$
et un revêtement de
$H=\{(g,g^{-1}) : g\in \mu _n\}$
et un revêtement de
![]() $S\times C$
de groupe de Galois
$S\times C$
de groupe de Galois
![]() $\mu _n^2$
. On obtient l’égalité par Künneth:
$\mu _n^2$
. On obtient l’égalité par Künneth:
 $$ \begin{align*} \mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}) = \mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}_1\times_L{\mathcal{T}}_2)^H &= ( \bigoplus\limits_{{\substack{\chi_1, \chi_2\in \mu_n^\lor }}}^{}{\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}}_1\times {\mathcal{T}}_2)[ \chi_1, \chi_2] }))^H\\ &=\bigoplus\limits_{{\substack{ q_1 +q_2=q}}}^{}{\bigoplus\limits_{{\substack{\chi\in \mu_n^\lor }}}^{}{\mathrm{ H}^{q_1}_{\mathrm{dR}} ({\mathcal{T}}_1)[ \chi]\otimes \mathrm{H}^{q_2}_{\mathrm{dR}} ({\mathcal{T}}_2)[ \chi]. }} \end{align*} $$
$$ \begin{align*} \mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}) = \mathrm{H}^{q}_{\mathrm{dR}}({\mathcal{T}}_1\times_L{\mathcal{T}}_2)^H &= ( \bigoplus\limits_{{\substack{\chi_1, \chi_2\in \mu_n^\lor }}}^{}{\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}}_1\times {\mathcal{T}}_2)[ \chi_1, \chi_2] }))^H\\ &=\bigoplus\limits_{{\substack{ q_1 +q_2=q}}}^{}{\bigoplus\limits_{{\substack{\chi\in \mu_n^\lor }}}^{}{\mathrm{ H}^{q_1}_{\mathrm{dR}} ({\mathcal{T}}_1)[ \chi]\otimes \mathrm{H}^{q_2}_{\mathrm{dR}} ({\mathcal{T}}_2)[ \chi]. }} \end{align*} $$
De même pour
![]() ${\mathcal {T}}_1\times _L{\mathcal {T}}_2'$
par rapport à
${\mathcal {T}}_1\times _L{\mathcal {T}}_2'$
par rapport à
![]() ${\mathcal {T}}'$
et
${\mathcal {T}}'$
et
![]() $S\times C'$
, on a
$S\times C'$
, on a
 $$ \begin{align*}\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}}') = \bigoplus\limits_{{\substack{ q_1 +q_2=q}}}^{}{\bigoplus\limits_{{\substack{\chi\in \mu_n^\lor }}}^{}{\mathrm{H}^{q_1}_{\mathrm{dR}} ({\mathcal{T}}_1)[ \chi]\otimes \mathrm{H}^{q_2}_{\mathrm{dR}} ({\mathcal{T}}_2')[ \chi] }}.\end{align*} $$
$$ \begin{align*}\mathrm{H}^{q}_{\mathrm{dR}} ({\mathcal{T}}') = \bigoplus\limits_{{\substack{ q_1 +q_2=q}}}^{}{\bigoplus\limits_{{\substack{\chi\in \mu_n^\lor }}}^{}{\mathrm{H}^{q_1}_{\mathrm{dR}} ({\mathcal{T}}_1)[ \chi]\otimes \mathrm{H}^{q_2}_{\mathrm{dR}} ({\mathcal{T}}_2')[ \chi] }}.\end{align*} $$
On en déduit le diagramme commutatif

Mais d’après 5.10, la flèche
![]() $\iota ^{*}$
est un isomorphisme et les deux flèches verticales sont des bijections. On peut alors appliquer 5.14 pour prouver le théorème 5.1.
$\iota ^{*}$
est un isomorphisme et les deux flèches verticales sont des bijections. On peut alors appliquer 5.14 pour prouver le théorème 5.1.
Supposons maintenant
![]() ${\mathcal {X}}$
semi-stable généralisé et
${\mathcal {X}}$
semi-stable généralisé et
![]() $\pi =\mathrm {Id}$
. On considère le tore monomial
$\pi =\mathrm {Id}$
. On considère le tore monomial
 $$\begin{align*}Y=\{\tilde{Z}=(T, Z_1,\cdots, Z_d): T\prod_{i=0}^d Z_i^{\alpha_i}=\varpi \text{ et } |T|\le \lambda^{1/\alpha_0}, |Z_{j_1} (s)|\leq \lambda, |Z_{j_2} (s)|=\beta, |Z_{j_3} (s)|\leq\beta\, \forall j_k\in J_k\}\end{align*}$$
$$\begin{align*}Y=\{\tilde{Z}=(T, Z_1,\cdots, Z_d): T\prod_{i=0}^d Z_i^{\alpha_i}=\varpi \text{ et } |T|\le \lambda^{1/\alpha_0}, |Z_{j_1} (s)|\leq \lambda, |Z_{j_2} (s)|=\beta, |Z_{j_3} (s)|\leq\beta\, \forall j_k\in J_k\}\end{align*}$$
et on peut écrire
![]() $C=Y(T^{1/\alpha _0})$
. En raisonnant de même sur
$C=Y(T^{1/\alpha _0})$
. En raisonnant de même sur
![]() $C'$
, on observe l’isomorphisme
$C'$
, on observe l’isomorphisme
![]() $\mathrm {H}^{*}_{\mathrm {dR}}(C)\cong \mathrm {H}^{*}_{\mathrm {dR}}(C')$
d’après 5.10 et on en déduit
$\mathrm {H}^{*}_{\mathrm {dR}}(C)\cong \mathrm {H}^{*}_{\mathrm {dR}}(C')$
d’après 5.10 et on en déduit
![]() $\mathrm {H}^{*}_{\mathrm {dR}}(S\times C)\cong \mathrm {H}^{*}_{\mathrm {dR}}(S\times C')$
par Künneth.
$\mathrm {H}^{*}_{\mathrm {dR}}(S\times C)\cong \mathrm {H}^{*}_{\mathrm {dR}}(S\times C')$
par Künneth.
6 Cohomologie de de Rham du premier revêtement de la tour de Drinfeld
Le but de ce chapitre est de calculer la ‘partie cuspidale’ de la cohomologie de de Rham de
![]() $\Sigma ^1$
. Cela utilise tous les résultats obtenus jusqu’à présent. Dans tout ce chapitre nous noterons
$\Sigma ^1$
. Cela utilise tous les résultats obtenus jusqu’à présent. Dans tout ce chapitre nous noterons
Théorème 6.1. Soit
![]() $\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to \breve {K}_N^{*}$
un caractère primitif. Il existe un isomorphisme n
$\theta : {\mathbb {F}}_{q^{d+1}}^{*}\to \breve {K}_N^{*}$
un caractère primitif. Il existe un isomorphisme n
et
![]() $\mathrm {H}^{r}_{\mathrm {dR},c}(\Sigma ^1_{\breve {K}_N})[\theta ]=0$
pour
$\mathrm {H}^{r}_{\mathrm {dR},c}(\Sigma ^1_{\breve {K}_N})[\theta ]=0$
pour
![]() $r\ne d$
.
$r\ne d$
.
Pour démontrer le théorème, on étudie la suite spectrale de Cech associée au recouvrement par les tubes (dans
![]() $\Sigma ^1$
) au-dessus des composantes irréductibles de la fibre spéciale de
$\Sigma ^1$
) au-dessus des composantes irréductibles de la fibre spéciale de
![]() ${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d $
(i.e., au recouvrement par la famille d’ouverts
${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d $
(i.e., au recouvrement par la famille d’ouverts
![]() $(\Sigma ^1_{ \operatorname {\mathrm {Ost}}(s)})_{s\in {\mathcal {B}}{\mathcal {T}}_0}$
):
$(\Sigma ^1_{ \operatorname {\mathrm {Ost}}(s)})_{s\in {\mathcal {B}}{\mathcal {T}}_0}$
):
Par dualité de Poincaré 2.2, on se ramène à étudier
![]() $\mathrm {H}^{r}_{\mathrm {dR}}(\Sigma ^1_{\operatorname {\mathrm {Ost}}(\sigma )})$
. Nous montrerons (cf. paragraphe 6.1) que, pour
$\mathrm {H}^{r}_{\mathrm {dR}}(\Sigma ^1_{\operatorname {\mathrm {Ost}}(\sigma )})$
. Nous montrerons (cf. paragraphe 6.1) que, pour
![]() $s\in {\mathcal {B}}{\mathcal {T}}_0$
, on a un isomorphisme n
$s\in {\mathcal {B}}{\mathcal {T}}_0$
, on a un isomorphisme n
 $$ \begin{align*}\mathrm{H}^{r}_{\mathrm{dR},c}(\Sigma^1_{\breve{K}_N, \operatorname{\mathrm{Ost}}(s)})[\theta] = \begin{cases} \mathrm{ H}^{d}_{\mathrm{rig},c}(\operatorname{\mathrm{DL}}_{{\mathbb{F}}}^d/\breve{K}_N )[\theta] & \text{si } r=d \\ 0 & \text{sinon} \end{cases}\end{align*} $$
$$ \begin{align*}\mathrm{H}^{r}_{\mathrm{dR},c}(\Sigma^1_{\breve{K}_N, \operatorname{\mathrm{Ost}}(s)})[\theta] = \begin{cases} \mathrm{ H}^{d}_{\mathrm{rig},c}(\operatorname{\mathrm{DL}}_{{\mathbb{F}}}^d/\breve{K}_N )[\theta] & \text{si } r=d \\ 0 & \text{sinon} \end{cases}\end{align*} $$
et (cf. paragraphe 6.2) que
![]() $\mathrm {H}^{r}_{\mathrm { dR},c}(\Sigma ^1_{\operatorname {\mathrm {Ost}}(\sigma )})[\theta ] =0$
pour
$\mathrm {H}^{r}_{\mathrm { dR},c}(\Sigma ^1_{\operatorname {\mathrm {Ost}}(\sigma )})[\theta ] =0$
pour
![]() $\mathrm {dim}(\sigma ) \ge 1$
. Ces deux résultats, dont la preuve utilise de manière cruciale le théorème 5.1, montrent la dégénérescence de la suite spectrale et permettent de conclure la preuve du théorème 6.1.
$\mathrm {dim}(\sigma ) \ge 1$
. Ces deux résultats, dont la preuve utilise de manière cruciale le théorème 5.1, montrent la dégénérescence de la suite spectrale et permettent de conclure la preuve du théorème 6.1.
6.1 Le tube au-dessus d’une composante irréductible
Le but de ce paragraphe est de calculer la cohomologie de de Rham du tube au-dessus d’une composante irréductible (i.e.,
![]() $\mathrm {H}^{r}_{\mathrm {dR}}(\Sigma ^1_{ \operatorname {\mathrm {Ost}}(s)})$
, plus précisément de démontrer le résultat suivant):
$\mathrm {H}^{r}_{\mathrm {dR}}(\Sigma ^1_{ \operatorname {\mathrm {Ost}}(s)})$
, plus précisément de démontrer le résultat suivant):
Proposition 6.2. Si
![]() $s\in {\mathcal {B}}{\mathcal {T}}_0$
est un sommet, il existe un isomorphisme n
$s\in {\mathcal {B}}{\mathcal {T}}_0$
est un sommet, il existe un isomorphisme n
 $$ \begin{align*}\mathrm{ H}^{r}_{\mathrm{dR},c}(\Sigma^1_{\breve{K}_N, \operatorname{\mathrm{Ost}}(s)})[\theta] = \begin{cases} \mathrm{ H}^{d}_{\mathrm{rig},c}(\operatorname{\mathrm{DL}}_{{\mathbb{F}}}^d/\breve{K}_N )[\theta] & \text{si } r=d \\ 0 & \text{sinon} \end{cases}.\end{align*} $$
$$ \begin{align*}\mathrm{ H}^{r}_{\mathrm{dR},c}(\Sigma^1_{\breve{K}_N, \operatorname{\mathrm{Ost}}(s)})[\theta] = \begin{cases} \mathrm{ H}^{d}_{\mathrm{rig},c}(\operatorname{\mathrm{DL}}_{{\mathbb{F}}}^d/\breve{K}_N )[\theta] & \text{si } r=d \\ 0 & \text{sinon} \end{cases}.\end{align*} $$
D’après le théorème 5.1 et la discussion dans le paragraphe précédent on a un isomorphisme naturel (induit par la restriction)
Pour étudier
![]() $ \mathrm {H}^{r}_{\mathrm {dR}}(\Sigma ^1_{ s})$
, nous devons rendre explicite le lien entre
$ \mathrm {H}^{r}_{\mathrm {dR}}(\Sigma ^1_{ s})$
, nous devons rendre explicite le lien entre
![]() $\Sigma ^1_s$
et la variété de Deligne-Lusztig
$\Sigma ^1_s$
et la variété de Deligne-Lusztig
![]() $\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d$
. Ce lien est établi dans [Reference Wang32, 2.3.8], mais nous allons donner l’argument pour le confort du lecteur.
$\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d$
. Ce lien est établi dans [Reference Wang32, 2.3.8], mais nous allons donner l’argument pour le confort du lecteur.
Lemme 6.3. La restriction
![]() $\Sigma ^1_{\breve {K}_N, s}$
du premier revêtement au-dessus d’un sommet admet un modèle entier lisse
$\Sigma ^1_{\breve {K}_N, s}$
du premier revêtement au-dessus d’un sommet admet un modèle entier lisse
![]() $\widehat {\Sigma }_s^{1}$
dont la fibre spéciale
$\widehat {\Sigma }_s^{1}$
dont la fibre spéciale
![]() $\overline {\Sigma }_s^1$
est isomorphe à la variété de Deligne-Lusztig
$\overline {\Sigma }_s^1$
est isomorphe à la variété de Deligne-Lusztig
![]() $\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d$
.
$\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d$
.
De plus, l’isomorphisme ci-dessus est
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)\times {\mathbb {F}}_{q^{d+1}}^{*}$
-équivariant.
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)\times {\mathbb {F}}_{q^{d+1}}^{*}$
-équivariant.
Grâce au lemme précédent et à 2.3 on obtient des isomorphismes
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)\times {\mathcal {O}}_D^{*}/ (1+ \Pi _D {\mathcal {O}}_D)$
-équivariants
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)\times {\mathcal {O}}_D^{*}/ (1+ \Pi _D {\mathcal {O}}_D)$
-équivariants
ce qui termine la preuve de la proposition 6.2.
Démonstration. On peut supposer que s est le sommet standard. L’énoncé du théorème 3.5 introduit une fonction inversible
![]() $u_1$
sur
$u_1$
sur
![]() ${\mathbb {H}}_{\breve {K}_N,s}^d$
voire même sur
${\mathbb {H}}_{\breve {K}_N,s}^d$
voire même sur
![]() ${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}_N},s}^d$
telle que
${\mathbb {H}}_{{\mathcal {O}}_{\breve {K}_N},s}^d$
telle que
![]() $\Sigma ^1_{\breve {K}_N,s}= {\mathbb {H}}_{\breve {K}_N,s}^d(u_1^{\frac {1}{N}})$
. La normalisation de
$\Sigma ^1_{\breve {K}_N,s}= {\mathbb {H}}_{\breve {K}_N,s}^d(u_1^{\frac {1}{N}})$
. La normalisation de
![]() ${\mathbb {H}}^d_{{\mathcal {O}}_{\breve {K}},s}$
dans
${\mathbb {H}}^d_{{\mathcal {O}}_{\breve {K}},s}$
dans
![]() $\Sigma ^1_{\breve {K}_N,s}$
fournit un modèle entier
$\Sigma ^1_{\breve {K}_N,s}$
fournit un modèle entier
![]() $\widehat {\Sigma }_{s}^{1}={\mathbb {H}}_{{\mathcal {O}}_{\breve {K}_N},s}^d(u_1^{\frac {1}{N}})$
de fibre spéciale
$\widehat {\Sigma }_{s}^{1}={\mathbb {H}}_{{\mathcal {O}}_{\breve {K}_N},s}^d(u_1^{\frac {1}{N}})$
de fibre spéciale
D’après 4.1, le revêtement de type Kummer
![]() $ {\mathbb {H}}_{\overline {{\mathbb {F}}},s}^d(u_1^{\frac {1}{N}})$
admet un isomorphisme
$ {\mathbb {H}}_{\overline {{\mathbb {F}}},s}^d(u_1^{\frac {1}{N}})$
admet un isomorphisme
![]() ${\mathbb {F}}_{q^{d+1}}^{*}$
-équivariant vers
${\mathbb {F}}_{q^{d+1}}^{*}$
-équivariant vers
![]() $\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d$
. Le reste de la preuve consiste à montrer qu’il est de plus
$\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d$
. Le reste de la preuve consiste à montrer qu’il est de plus
![]() $G^{\circ }:=\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)$
-équivariant.
$G^{\circ }:=\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K)$
-équivariant.
Rappelons que toutes les actions possibles de
![]() $G^{\circ }$
sur
$G^{\circ }$
sur
![]() $ \overline {\Sigma }^1_s$
ou sur
$ \overline {\Sigma }^1_s$
ou sur
![]() ${\Sigma }^1_s$
commutant avec le revêtement se déduisent l’une de l’autre en tordant par un caractère
${\Sigma }^1_s$
commutant avec le revêtement se déduisent l’une de l’autre en tordant par un caractère
d’après [Reference Junger26, Remarque 4.12]. Plus précisément, pour T une racine N-ième de
![]() $u_1$
dans
$u_1$
dans
![]() ${\mathscr {O}}(\overline {\Sigma }^1_s )={\mathscr {O}}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d )$
ou dans
${\mathscr {O}}(\overline {\Sigma }^1_s )={\mathscr {O}}(\operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d )$
ou dans
![]() ${\mathscr {O}}({\Sigma }^1_s )$
, le caractère
${\mathscr {O}}({\Sigma }^1_s )$
, le caractère
![]() $\chi $
associé à deux actions de
$\chi $
associé à deux actions de
![]() $G^{\circ }$
notées
$G^{\circ }$
notées
![]() $g\mapsto [g]_1$
et
$g\mapsto [g]_1$
et
![]() $g\mapsto [g]_2$
est donné par
$g\mapsto [g]_2$
est donné par
![]() $\chi (g)=[g]_1\cdot T / [g]_2 \cdot T $
. On en déduit aussi que l’on a une bijection entre les actions de
$\chi (g)=[g]_1\cdot T / [g]_2 \cdot T $
. On en déduit aussi que l’on a une bijection entre les actions de
![]() $G^{\circ }$
sur
$G^{\circ }$
sur
![]() $ \overline {\Sigma }^1_s$
et celles sur
$ \overline {\Sigma }^1_s$
et celles sur
![]() ${\Sigma }^1_s$
qui préserve les caractères
${\Sigma }^1_s$
qui préserve les caractères
![]() $\chi $
.
$\chi $
.
Nous étudions maintenant le cas où
![]() $g\mapsto [g]_1$
(resp.
$g\mapsto [g]_1$
(resp.
![]() $g\mapsto [g]_2$
) est l’action provenant de
$g\mapsto [g]_2$
) est l’action provenant de
![]() $\Sigma ^1$
(resp. de
$\Sigma ^1$
(resp. de
![]() $\operatorname {\mathrm {DL}}_{{\mathbb {F}}}^d$
). Il s’agit de prouver que le caractère obtenu est trivial. On voit aisément que ce dernier se factorise via la flèche
$\operatorname {\mathrm {DL}}_{{\mathbb {F}}}^d$
). Il s’agit de prouver que le caractère obtenu est trivial. On voit aisément que ce dernier se factorise via la flèche
![]() $G^{\circ } \xrightarrow []{\det } {\mathcal {O}}_{K}^{*} \to {\mathbb {F}}^{*}$
car
$G^{\circ } \xrightarrow []{\det } {\mathcal {O}}_{K}^{*} \to {\mathbb {F}}^{*}$
car
![]() $1+\varpi {\mathcal {O}}_K$
est N-divisible. Comme
$1+\varpi {\mathcal {O}}_K$
est N-divisible. Comme
![]() ${\mathbb {F}}^{*}$
est cyclique, il suffit de raisonner sur une matrice
${\mathbb {F}}^{*}$
est cyclique, il suffit de raisonner sur une matrice
![]() $g\in G^{\circ }$
telle que
$g\in G^{\circ }$
telle que
![]() $\det g$
engendre
$\det g$
engendre
![]() ${\mathbb {F}}^{*}$
et sur la fibre d’un point
${\mathbb {F}}^{*}$
et sur la fibre d’un point
![]() $y\in {\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d( {\mathcal {O}}_{\breve {K}})$
fixé par g.
$y\in {\mathbb {H}}_{{\mathcal {O}}_{\breve {K}}}^d( {\mathcal {O}}_{\breve {K}})$
fixé par g.
Expliquons comment choisir cette matrice. Observons que la norme
![]() $N: {\mathbb {F}}_{q^{d+1}}^{*}\to {\mathbb {F}}^{*}$
est surjectiveFootnote
12
. On se donne
$N: {\mathbb {F}}_{q^{d+1}}^{*}\to {\mathbb {F}}^{*}$
est surjectiveFootnote
12
. On se donne
![]() $\lambda \in {\mathbb {F}}_{q^{d+1}}$
un élément dont la norme engendre
$\lambda \in {\mathbb {F}}_{q^{d+1}}$
un élément dont la norme engendre
![]() ${\mathbb {F}}^{*}$
si bien que
${\mathbb {F}}^{*}$
si bien que
![]() ${\mathbb {F}}_{q^{d+1}}= {\mathbb {F}}[\lambda ] $
et le polynôme minimal sur
${\mathbb {F}}_{q^{d+1}}= {\mathbb {F}}[\lambda ] $
et le polynôme minimal sur
![]() ${\mathbb {F}}$
de
${\mathbb {F}}$
de
![]() $\lambda $
est de degré
$\lambda $
est de degré
![]() $d+1$
. De plus, n’importe quel relevé unitaire P sur
$d+1$
. De plus, n’importe quel relevé unitaire P sur
![]() ${\mathcal {O}}_{K}$
est encore irréductible de degré
${\mathcal {O}}_{K}$
est encore irréductible de degré
![]() $d+1$
. Donnons-nous une matrice
$d+1$
. Donnons-nous une matrice
![]() $g\in \operatorname {\mathrm {M}}_{d+1}({\mathcal {O}}_K)$
de polynôme caractéristique P (par exemple la matrice compagnon associée). Ainsi, g est dans
$g\in \operatorname {\mathrm {M}}_{d+1}({\mathcal {O}}_K)$
de polynôme caractéristique P (par exemple la matrice compagnon associée). Ainsi, g est dans
![]() $G^{\circ }$
, régulière elliptique et son déterminant engendre
$G^{\circ }$
, régulière elliptique et son déterminant engendre
![]() ${\mathbb {F}}^{*}$
.
${\mathbb {F}}^{*}$
.
L’élément g admet
![]() $d+1$
points fixes distincts dans
$d+1$
points fixes distincts dans
![]() ${\mathbb {P}}^{d}({\mathcal {O}}_{C})$
qui correspondent aux droites propres de g dans
${\mathbb {P}}^{d}({\mathcal {O}}_{C})$
qui correspondent aux droites propres de g dans
![]() $C^{d+1}$
. Montrons qu’elles sont toutes dans
$C^{d+1}$
. Montrons qu’elles sont toutes dans
![]() ${\mathbb {H}}^d_{K,s}(C)$
. Pour cela, pour tout vecteur propre
${\mathbb {H}}^d_{K,s}(C)$
. Pour cela, pour tout vecteur propre
![]() $v\in C^{d+1}$
que l’on suppose unimodulaire à normalisation près, nous devons prouver que les coordonnées de v modulo
$v\in C^{d+1}$
que l’on suppose unimodulaire à normalisation près, nous devons prouver que les coordonnées de v modulo
![]() $\varpi $
sont libres sur
$\varpi $
sont libres sur
![]() ${\mathbb {F}}$
. Supposons que ce ne soit pas le cas et prenons
${\mathbb {F}}$
. Supposons que ce ne soit pas le cas et prenons
![]() $a\in {\mathbb {F}}^{d+1}\backslash \{0\}$
tel que
$a\in {\mathbb {F}}^{d+1}\backslash \{0\}$
tel que
![]() $\langle a, v \rangle =0$
. Ainsi
$\langle a, v \rangle =0$
. Ainsi
et
![]() $v^{\perp }\cap {\mathbb {F}}^{d+1}$
est stable sous l’action de
$v^{\perp }\cap {\mathbb {F}}^{d+1}$
est stable sous l’action de
![]() $g^t$
. Comme le polynôme caractéristique P de
$g^t$
. Comme le polynôme caractéristique P de
![]() $g^t$
est irréductible surFootnote
13
$g^t$
est irréductible surFootnote
13
![]() ${\mathbb {F}}$
,
${\mathbb {F}}$
,
![]() $v^{\perp } \cap {\mathbb {F}}^{d+1}= {\mathbb {F}}^{d+1}$
ie.
$v^{\perp } \cap {\mathbb {F}}^{d+1}= {\mathbb {F}}^{d+1}$
ie.
![]() $v=0$
, d’où une contradiction.
$v=0$
, d’où une contradiction.
Prenons
![]() $y\in {\mathbb {H}}^d_{{\mathcal {O}}_{\breve {K}},s}({\mathcal {O}}_{C}) $
le point fixe de g correspondant à la valeur propre
$y\in {\mathbb {H}}^d_{{\mathcal {O}}_{\breve {K}},s}({\mathcal {O}}_{C}) $
le point fixe de g correspondant à la valeur propre
![]() $\lambda $
et
$\lambda $
et
![]() $\overline {y}\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}},s }(\overline {{\mathbb {F}}})$
sa spécialisation. D’après 4.1, un point
$\overline {y}\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}},s }(\overline {{\mathbb {F}}})$
sa spécialisation. D’après 4.1, un point
![]() $x\in \operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d (\overline {{\mathbb {F}}})$
corresponds à un vecteur
$x\in \operatorname {\mathrm {DL}}_{\overline {{\mathbb {F}}}}^d (\overline {{\mathbb {F}}})$
corresponds à un vecteur
![]() $x=(x_0,\ldots , x_d)$
dans
$x=(x_0,\ldots , x_d)$
dans
![]() $\overline {{\mathbb {F}}}^{d+1}$
tel que
$\overline {{\mathbb {F}}}^{d+1}$
tel que
![]() $\tilde {u}_1(x)=1$
. De plus, x est dans la fibre
$\tilde {u}_1(x)=1$
. De plus, x est dans la fibre
![]() $ \pi ^{-1}(\overline {y})$
, si x engendre la droite
$ \pi ^{-1}(\overline {y})$
, si x engendre la droite
![]() $\overline {y}$
. Dans ce cas,
$\overline {y}$
. Dans ce cas,
![]() $[g]_2\cdot x = \lambda x$
. Mais d’après la description de l’isomorphisme
$[g]_2\cdot x = \lambda x$
. Mais d’après la description de l’isomorphisme
![]() $\operatorname {\mathrm {DL}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}}) \stackrel {\sim }{\rightarrow } {\mathbb {H}}_{\overline {{\mathbb {F}}},s}^d(u_1^{\frac {1}{N}})$
donnée dans 4.2, on a
$\operatorname {\mathrm {DL}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}}) \stackrel {\sim }{\rightarrow } {\mathbb {H}}_{\overline {{\mathbb {F}}},s}^d(u_1^{\frac {1}{N}})$
donnée dans 4.2, on a
![]() $T=\frac {1}{x_0}$
et donc
$T=\frac {1}{x_0}$
et donc
![]() $[g]_2\cdot T= \lambda ^{-1}T$
sur
$[g]_2\cdot T= \lambda ^{-1}T$
sur
![]() $ \pi ^{-1}(\overline {y})$
.
$ \pi ^{-1}(\overline {y})$
.
Decrivons maintenant l’action provenant du premier revêtement
![]() $\Sigma ^1$
. D’aprèsFootnote
14
[Reference Junger26, Corollaire 3.10], la restriction
$\Sigma ^1$
. D’aprèsFootnote
14
[Reference Junger26, Corollaire 3.10], la restriction
![]() ${\mathfrak {X}}[\Pi _D]_s$
des points de torsion du module universel
${\mathfrak {X}}[\Pi _D]_s$
des points de torsion du module universel
![]() ${\mathfrak {X}}[\Pi _D]$
au dessus du sommet s est affine de sections
${\mathfrak {X}}[\Pi _D]$
au dessus du sommet s est affine de sections
Rappelons que
![]() ${\mathscr {O}}({\Sigma }_s^1)={\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)[1/\tilde {T}, 1/\varpi ]$
et
${\mathscr {O}}({\Sigma }_s^1)={\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)[1/\tilde {T}, 1/\varpi ]$
et
![]() $\tilde {T}=\varpi _N T$
dans
$\tilde {T}=\varpi _N T$
dans
![]() ${\mathscr {O}}({\Sigma }_s^1)\otimes \breve {K}_N$
. Ainsi, calculer
${\mathscr {O}}({\Sigma }_s^1)\otimes \breve {K}_N$
. Ainsi, calculer
![]() $[g]_1 \cdot \tilde {T}$
dans
$[g]_1 \cdot \tilde {T}$
dans
![]() ${\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)$
revient à déterminer
${\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)$
revient à déterminer
![]() $[g]_1 \cdot T$
dans
$[g]_1 \cdot T$
dans
![]() ${\mathscr {O}}({\Sigma }_s^1)$
ou dans
${\mathscr {O}}({\Sigma }_s^1)$
ou dans
![]() ${\mathscr {O}}(\overline {\Sigma }_s^1)$
. Plaçons-nous donc sur
${\mathscr {O}}(\overline {\Sigma }_s^1)$
. Plaçons-nous donc sur
![]() ${\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)$
et plus précisément sur l’idéal d’augmentation
${\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)$
et plus précisément sur l’idéal d’augmentation
![]() ${\mathcal {I}}=\bigoplus _{i = 1}^{N} \tilde {T}^i {\mathscr {O}}({\mathbb {H}}^d_{{\mathcal {O}}_{\breve {K}},s})$
de
${\mathcal {I}}=\bigoplus _{i = 1}^{N} \tilde {T}^i {\mathscr {O}}({\mathbb {H}}^d_{{\mathcal {O}}_{\breve {K}},s})$
de
![]() ${\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)$
. La description précédente de l’idéal d’augmentation est en fait la décomposition en partie isotypique pour l’action de
${\mathscr {O}}({\mathfrak {X}}[\Pi _D]_s)$
. La description précédente de l’idéal d’augmentation est en fait la décomposition en partie isotypique pour l’action de
![]() ${\mathcal {O}}_{(d+1)}^{*}(\subset {\mathcal {O}}_{D}^{*})$
. Le cotangent de
${\mathcal {O}}_{(d+1)}^{*}(\subset {\mathcal {O}}_{D}^{*})$
. Le cotangent de
![]() ${\mathfrak {X}}[\Pi _D]_s$
s'écrit:
${\mathfrak {X}}[\Pi _D]_s$
s'écrit:
Mais, on a aussi
il suffit donc de montrer que de comprendre l'action de la matrice g fixée sur la partie isotypique
![]() $(\mathrm{Lie} \mathfrak{X}_s )_d|_{\bar{y}}$
correspondante.
$(\mathrm{Lie} \mathfrak{X}_s )_d|_{\bar{y}}$
correspondante.
Utilisons la théorie de Cartier pour décrire le plan tangent. D’après 3.3, un point fermé
![]() $z\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}})$
correspond à un coupleFootnote
15
$z\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}})$
correspond à un coupleFootnote
15
![]() $(X,\rho )$
où X est un
$(X,\rho )$
où X est un
![]() ${\mathcal {O}}_D$
-module formel spécial sur
${\mathcal {O}}_D$
-module formel spécial sur
![]() $\overline {{\mathbb {F}}}$
et
$\overline {{\mathbb {F}}}$
et
![]() $\rho $
une quasi-isogénie
$\rho $
une quasi-isogénie
![]() $ \Phi \rightarrow X$
de hauteur
$ \Phi \rightarrow X$
de hauteur
![]() $0$
. Aux modules X et
$0$
. Aux modules X et
![]() $\Phi $
correspondent des modules de Cartier
$\Phi $
correspondent des modules de Cartier
![]() $M_X $
et
$M_X $
et
![]() $M_{\Phi } $
surFootnote
16
$M_{\Phi } $
surFootnote
16
![]() ${\mathcal {O}}_{\breve {K}}\langle F, V \rangle $
(ainsi qu’un opérateur
${\mathcal {O}}_{\breve {K}}\langle F, V \rangle $
(ainsi qu’un opérateur
![]() $\Pi $
qui commute à F, V) qui sont libres de rang
$\Pi $
qui commute à F, V) qui sont libres de rang
![]() $4$
sur
$4$
sur
![]() ${\mathcal {O}}_{\breve {K}}$
et la quasi-isogénie
${\mathcal {O}}_{\breve {K}}$
et la quasi-isogénie
![]() $\rho $
induit un isomorphisme
$\rho $
induit un isomorphisme
![]() $M_{X}[\frac {1}{p}] \stackrel {\sim }{\rightarrow } M_{\Phi } [\frac {1}{p}]$
. Nous allons chercher à déterminer dans la suite les couples
$M_{X}[\frac {1}{p}] \stackrel {\sim }{\rightarrow } M_{\Phi } [\frac {1}{p}]$
. Nous allons chercher à déterminer dans la suite les couples
![]() $(M_X,\rho )$
qui correspondent aux points de
$(M_X,\rho )$
qui correspondent aux points de
![]() ${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})\subset {\mathbb {H}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}})$
. Pour cela, nous aurons besoin de quelques résultats classiques sur les modules de Cartier spéciaux.
${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})\subset {\mathbb {H}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}})$
. Pour cela, nous aurons besoin de quelques résultats classiques sur les modules de Cartier spéciaux.
L’action de
![]() ${\mathcal {O}}_{(d+1)}$
sur
${\mathcal {O}}_{(d+1)}$
sur
![]() $M_X$
et
$M_X$
et
![]() $M_{\Phi }$
induit des
$M_{\Phi }$
induit des
![]() $\mathbb{Z}/(d+1)\mathbb{Z}$
-graduations
$\mathbb{Z}/(d+1)\mathbb{Z}$
-graduations
![]() $M_X= \sum _{i\in {\mathbb {Z}}/(d+1){\mathbb {Z}}} M_{X,i}$
(de même pour
$M_X= \sum _{i\in {\mathbb {Z}}/(d+1){\mathbb {Z}}} M_{X,i}$
(de même pour
![]() $M_{\Phi }$
) suivant les plongements de
$M_{\Phi }$
) suivant les plongements de
![]() ${\mathcal {O}}_{(d+1)}$
dans
${\mathcal {O}}_{(d+1)}$
dans
![]() ${\mathcal {O}}_{\breve {K}}$
. Les opérateurs V,
${\mathcal {O}}_{\breve {K}}$
. Les opérateurs V,
![]() $\Pi $
sont de degré
$\Pi $
sont de degré
![]() $1$
et F est de degré
$1$
et F est de degré
![]() $-1$
. On a le résultat classique suivant:
$-1$
. On a le résultat classique suivant:
Lemme 6.4. Soit
![]() $X/\overline {{\mathbb {F}}}$
un
$X/\overline {{\mathbb {F}}}$
un
![]() ${\mathcal {O}}_D$
-module formel spécial de dimension
${\mathcal {O}}_D$
-module formel spécial de dimension
![]() $(d+1)$
et de hauteur
$(d+1)$
et de hauteur
![]() $(d+1)^2$
et
$(d+1)^2$
et
![]() $M_X$
le module de Cartier associé. On a les points suivants:
$M_X$
le module de Cartier associé. On a les points suivants:
-
1. On a une identification
 $\operatorname {\mathrm {Lie}} X \cong M_X/VM_X$
et les parties isotypiques sont de la forme
$\operatorname {\mathrm {Lie}} X \cong M_X/VM_X$
et les parties isotypiques sont de la forme
 $(\operatorname {\mathrm {Lie}} X)_i=M_{X,i}/VM_{X,i-1}$
.
$(\operatorname {\mathrm {Lie}} X)_i=M_{X,i}/VM_{X,i-1}$
. -
2. Pour tout
 $i\in {\mathbb {Z}}/(d+1){\mathbb {Z}}$
, on a
$i\in {\mathbb {Z}}/(d+1){\mathbb {Z}}$
, on a
 $[M_{X,i},VM_{X,i-1}]=[M_{X,i},\Pi M_{X,i-1}]=1$
et
$[M_{X,i},VM_{X,i-1}]=[M_{X,i},\Pi M_{X,i-1}]=1$
et
 $[M_{X,i},FM_{X,i+1}]=d$
.
$[M_{X,i},FM_{X,i+1}]=d$
. -
3. Soit
 $i\in {\mathbb {Z}}/(d+1){\mathbb {Z}}$
, les points suivants sont équivalents :
$i\in {\mathbb {Z}}/(d+1){\mathbb {Z}}$
, les points suivants sont équivalents :-
(a)
 $\Pi :(\operatorname {\mathrm {Lie}} X)_i\to (\operatorname {\mathrm {Lie}} X)_{i+1}$
est nulle,
$\Pi :(\operatorname {\mathrm {Lie}} X)_i\to (\operatorname {\mathrm {Lie}} X)_{i+1}$
est nulle, -
(b)
 $\Pi M_{X,i}\subset VM_{X,i}$
,
$\Pi M_{X,i}\subset VM_{X,i}$
, -
(c)
 $\Pi M_{X,i}=VM_{X,i}$
,
$\Pi M_{X,i}=VM_{X,i}$
, -
(d)
 $M_{X,i+1}\neq \Pi M_{X,i} +VM_{X,i}$
,
$M_{X,i+1}\neq \Pi M_{X,i} +VM_{X,i}$
, -
(e)
 $M_{X,i}=M_{X,i}^{V^{-1}\Pi }\otimes _{{\mathcal {O}}_K}{\mathcal {O}}_{\breve {K}}$
où
$M_{X,i}=M_{X,i}^{V^{-1}\Pi }\otimes _{{\mathcal {O}}_K}{\mathcal {O}}_{\breve {K}}$
où
 $M_{X,i}^{V^{-1}\Pi }=\{m\in M_{X,i} : V m=\Pi m \}$
.
$M_{X,i}^{V^{-1}\Pi }=\{m\in M_{X,i} : V m=\Pi m \}$
.
Lorsque ces hypothèses sont vérifiées, on dit que i est un indice critique.
-
-
4. Il existe au moins un indice critique.
Démonstration. Pour
![]() $1.$
, la deuxième assertion découle de la première qui est prouvée dans [Reference Zink36, Th. 4.23]. Le reste a été prouvé dans [Reference Boutot and Carayol4, §II.5] quand
$1.$
, la deuxième assertion découle de la première qui est prouvée dans [Reference Zink36, Th. 4.23]. Le reste a été prouvé dans [Reference Boutot and Carayol4, §II.5] quand
![]() $d=1$
. La traduction de ces arguments en dimension quelconque est transparente, mais nous en donnons quelques explications succinctes. Pour
$d=1$
. La traduction de ces arguments en dimension quelconque est transparente, mais nous en donnons quelques explications succinctes. Pour
![]() $2.$
l’égalité
$2.$
l’égalité
![]() $[M_{X,i},VM_{X,i-1}]=1$
provient du caractère spécial. Le reste se déduit du fait que
$[M_{X,i},VM_{X,i-1}]=1$
provient du caractère spécial. Le reste se déduit du fait que
![]() $\Pi $
, V, F commutent entre eux, et des identités
$\Pi $
, V, F commutent entre eux, et des identités
![]() $[M_{X},\varpi M_{X}]=(d+1)^2$
(la hauteur de X) et
$[M_{X},\varpi M_{X}]=(d+1)^2$
(la hauteur de X) et
![]() $FV=\Pi ^{d+1}=\varpi $
. Pour
$FV=\Pi ^{d+1}=\varpi $
. Pour
![]() $3.$
,
$3.$
,
![]() $(a)$
et
$(a)$
et
![]() $(b)$
sont équivalents d’après
$(b)$
sont équivalents d’après
![]() $1$
. Le point
$1$
. Le point
![]() $2.$
fournit le sens non-trivial de l’équivalence de
$2.$
fournit le sens non-trivial de l’équivalence de
![]() $(c)$
avec
$(c)$
avec
![]() $(a)$
,
$(a)$
,
![]() $(b)$
(idem pour
$(b)$
(idem pour
![]() $(d)\Leftrightarrow (c)$
). Pour
$(d)\Leftrightarrow (c)$
). Pour
![]() $(c)\Rightarrow (e)$
, on applique la classification de Dieudonné-Manin à l’isocrystal
$(c)\Rightarrow (e)$
, on applique la classification de Dieudonné-Manin à l’isocrystal
![]() $(M_{X,i}[1/p],V^{-1}\Pi )$
(l’autre sens est clair). Pour
$(M_{X,i}[1/p],V^{-1}\Pi )$
(l’autre sens est clair). Pour
![]() $4.$
, on observe que la flèche
$4.$
, on observe que la flèche
![]() $\Pi ^{d+1}=\varpi : M_X/VM_X \to M_X/VM_X$
est nulle.
$\Pi ^{d+1}=\varpi : M_X/VM_X \to M_X/VM_X$
est nulle.
Pour simplifier, nous supposerons que tous les indices de
![]() $M_{\Phi }$
sont critiques. Dans ce cas, un couple
$M_{\Phi }$
sont critiques. Dans ce cas, un couple
![]() $(M_X,\rho )$
est dans
$(M_X,\rho )$
est dans
![]() ${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})$
si et seulement si
${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})$
si et seulement si
![]() $\rho M_{X,d}=M_{\Phi ,d}$
et d est le seul indice critique de
$\rho M_{X,d}=M_{\Phi ,d}$
et d est le seul indice critique de
![]() $M_X$
. Pour un tel couple, on a une suite d’inclusion
$M_X$
. Pour un tel couple, on a une suite d’inclusion
qui définit une droite (d’après le point 4. et 2. de 6.4)
![]() $D:=\Pi ^d M_{X,0}/ \varpi M_{X,d}$
dans
$D:=\Pi ^d M_{X,0}/ \varpi M_{X,d}$
dans
![]() $M_{X,d}/ \varpi M_{X,d}$
et donc une flèche
$M_{X,d}/ \varpi M_{X,d}$
et donc une flèche
Grâce au point 3. (e) de 6.4, on peut identifier
 $$\begin{align*} \mathbb{P}(M_{X,d}^{V^{-1}\Pi}/\varpi )\cong\mathbb{P}(\mathbb{F}), \ \ \ \mathbb{P}(M_{X,d}/\varpi )\backslash \bigcup_{H\in \mathbb{P}(M_{X,d}^{V^{-1}\Pi}/\varpi )}H\cong\mathbb{P}^d(\bar{\mathbb{F}})\backslash \bigcup_{H\in \mathbb{P}^d(\mathbb{F})}H \end{align*}$$
$$\begin{align*} \mathbb{P}(M_{X,d}^{V^{-1}\Pi}/\varpi )\cong\mathbb{P}(\mathbb{F}), \ \ \ \mathbb{P}(M_{X,d}/\varpi )\backslash \bigcup_{H\in \mathbb{P}(M_{X,d}^{V^{-1}\Pi}/\varpi )}H\cong\mathbb{P}^d(\bar{\mathbb{F}})\backslash \bigcup_{H\in \mathbb{P}^d(\mathbb{F})}H \end{align*}$$
et
![]() $\mathrm{GL}_{d+1}(\mathbb{F})\cong \mathrm{GL}((M_{X,d}^{V^{-1}\Pi}/\varpi)$
. On en déduit une action de
$\mathrm{GL}_{d+1}(\mathbb{F})\cong \mathrm{GL}((M_{X,d}^{V^{-1}\Pi}/\varpi)$
. On en déduit une action de
![]() $G^{\circ}$
par inflation
$G^{\circ}$
par inflation
![]() $\mathbb{P}^d(\bar{\mathbb{F}})\backslash \bigcup_{H\in \mathbb{P}^d(\mathbb{F})}H$
. Grâce à ces constructions, on peut décrire explicitement la restriction de l’isomorphisme dans 3.3 sur les points géométriques de
$\mathbb{P}^d(\bar{\mathbb{F}})\backslash \bigcup_{H\in \mathbb{P}^d(\mathbb{F})}H$
. Grâce à ces constructions, on peut décrire explicitement la restriction de l’isomorphisme dans 3.3 sur les points géométriques de
![]() ${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}$
.
${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}$
.
Lemme 6.5. L’application
![]() $\psi $
définie précédemment induit une bijection
$\psi $
définie précédemment induit une bijection
![]() $G^{\circ }$
-équivariante:
$G^{\circ }$
-équivariante:
 $$\begin{align*}{\mathbb{H}}^d_{\overline{{\mathbb{F}}},s}(\overline{{\mathbb{F}}}) \stackrel{\sim}{\rightarrow} {\mathbb{P}}^d(\overline{{\mathbb{F}}})\backslash \bigcup_{H\in {\mathbb{P}}^d({\mathbb{F}})}H.\end{align*}$$
$$\begin{align*}{\mathbb{H}}^d_{\overline{{\mathbb{F}}},s}(\overline{{\mathbb{F}}}) \stackrel{\sim}{\rightarrow} {\mathbb{P}}^d(\overline{{\mathbb{F}}})\backslash \bigcup_{H\in {\mathbb{P}}^d({\mathbb{F}})}H.\end{align*}$$
Démonstration. Notons qu’un couple
![]() $(M_X,\rho )$
dans
$(M_X,\rho )$
dans
![]() ${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})$
est déterminé par la donnée des inclusions
${\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})$
est déterminé par la donnée des inclusions
![]() $\rho M_{X,i}\subset M_{\Phi } [\frac {1}{p}]$
. Par hypothèse, il suffit d’étudier les cas
$\rho M_{X,i}\subset M_{\Phi } [\frac {1}{p}]$
. Par hypothèse, il suffit d’étudier les cas
![]() $i\neq d$
. Comme aucun de ces indices ne sont critiques, on a les identités (cf 3. (d) dans 6.4)
$i\neq d$
. Comme aucun de ces indices ne sont critiques, on a les identités (cf 3. (d) dans 6.4)
et le sous-module
![]() $M_{X,0}$
détermine
$M_{X,0}$
détermine
![]() $M_{X,1}, \dots , M_{X,d-1}$
. Revenons à
$M_{X,1}, \dots , M_{X,d-1}$
. Revenons à
![]() $\psi $
, la droite
$\psi $
, la droite
![]() $\Pi ^d M_{X,0}/ \varpi M_{X,d}\subset M_{X,d}/ \varpi M_{X,d}$
détermine
$\Pi ^d M_{X,0}/ \varpi M_{X,d}\subset M_{X,d}/ \varpi M_{X,d}$
détermine
![]() $\rho \Pi ^d M_{X,0}$
(car
$\rho \Pi ^d M_{X,0}$
(car
![]() $\rho M_{X,d}$
et
$\rho M_{X,d}$
et
![]() $\rho \varpi M_{X,d}$
sont fixés) et donc le module
$\rho \varpi M_{X,d}$
sont fixés) et donc le module
![]() $\rho M_{X,0}$
par injectivité de la multiplication par
$\rho M_{X,0}$
par injectivité de la multiplication par
![]() $\Pi $
. Dit autrement, l’application
$\Pi $
. Dit autrement, l’application
![]() $\psi $
est injective.
$\psi $
est injective.
Il reste à prouver que l’image de cette flèche est l’ouvert décrit dans l’énoncé. Prenons un couple
![]() $(M_X,\rho )\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}})$
tel que
$(M_X,\rho )\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}}}(\overline {{\mathbb {F}}})$
tel que
![]() $\rho M_{X, d}=M_{\Phi ,d}$
et on fixe
$\rho M_{X, d}=M_{\Phi ,d}$
et on fixe
![]() $m_0\in M_{X,0}\backslash V M_{X,d}$
. En particulier,
$m_0\in M_{X,0}\backslash V M_{X,d}$
. En particulier,
![]() $m_0$
engendre
$m_0$
engendre
![]() $\operatorname {\mathrm {Lie}} (X)_0$
. Le point crucial est d’observer l’équivalence suivante: d est le seul indice critique si et seulement si
$\operatorname {\mathrm {Lie}} (X)_0$
. Le point crucial est d’observer l’équivalence suivante: d est le seul indice critique si et seulement si
![]() $(\Pi ^i V^{d-i} m_0)_i$
est une
$(\Pi ^i V^{d-i} m_0)_i$
est une
![]() $\overline {{\mathbb {F}}}$
-base de
$\overline {{\mathbb {F}}}$
-base de
![]() $M_{X,d}/\varpi M_{X,d}$
. Supposons le deuxième hypothèse, le module suivant est contenue dans
$M_{X,d}/\varpi M_{X,d}$
. Supposons le deuxième hypothèse, le module suivant est contenue dans
![]() $V M_{X,d-1}$
et est d’indice
$V M_{X,d-1}$
et est d’indice
![]() $1$
dans
$1$
dans
![]() $M_{X,d}$
$M_{X,d}$
Il est donc confondu avec
![]() $VM_{X,d-1}$
d’après le point 2. de 6.4. Ainsi,
$VM_{X,d-1}$
d’après le point 2. de 6.4. Ainsi,
![]() $\Pi ^d m_0$
engendre
$\Pi ^d m_0$
engendre
![]() $\operatorname {\mathrm {Lie}} (X)_d$
et la flèche
$\operatorname {\mathrm {Lie}} (X)_d$
et la flèche
![]() $\Pi ^{ d} :\operatorname {\mathrm {Lie}} (X)_0\to \operatorname {\mathrm {Lie}} (X)_d$
est non nulle ce qui montre que d est le seul indice critique. Réciproquement, supposons les indices
$\Pi ^{ d} :\operatorname {\mathrm {Lie}} (X)_0\to \operatorname {\mathrm {Lie}} (X)_d$
est non nulle ce qui montre que d est le seul indice critique. Réciproquement, supposons les indices
![]() $0,\dots , d-1$
non critiques et établissons d’abord par récurrence sur
$0,\dots , d-1$
non critiques et établissons d’abord par récurrence sur
![]() $0\le k\le d$
:
$0\le k\le d$
:
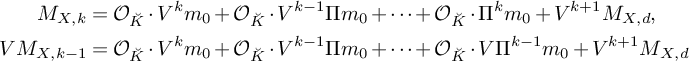 $$\begin{align*}M_{X,k}&= {\mathcal{O}}_{\breve{K}}\cdot V^k m_0 +{\mathcal{O}}_{\breve{K}}\cdot V^{k-1}\Pi m_0+\cdots +{\mathcal{O}}_{\breve{K}}\cdot\Pi^k m_0 +V^{k+1} M_{X,d},\\V M_{X,k-1}&={\mathcal{O}}_{\breve{K}}\cdot V^k m_0 + {\mathcal{O}}_{\breve{K}}\cdot V^{k-1}\Pi m_0+\cdots +{\mathcal{O}}_{\breve{K}}\cdot V\Pi^{k-1} m_0 +V^{k+1} M_{X,d} \end{align*}$$
$$\begin{align*}M_{X,k}&= {\mathcal{O}}_{\breve{K}}\cdot V^k m_0 +{\mathcal{O}}_{\breve{K}}\cdot V^{k-1}\Pi m_0+\cdots +{\mathcal{O}}_{\breve{K}}\cdot\Pi^k m_0 +V^{k+1} M_{X,d},\\V M_{X,k-1}&={\mathcal{O}}_{\breve{K}}\cdot V^k m_0 + {\mathcal{O}}_{\breve{K}}\cdot V^{k-1}\Pi m_0+\cdots +{\mathcal{O}}_{\breve{K}}\cdot V\Pi^{k-1} m_0 +V^{k+1} M_{X,d} \end{align*}$$
Le cas
![]() $k=0$
est une conséquence directe de la définition de
$k=0$
est une conséquence directe de la définition de
![]() $m_0$
. Pour l’hérédité, cela découle de la relation
$m_0$
. Pour l’hérédité, cela découle de la relation
![]() $M_{X,k+1}=\Pi M_{X,k}+V M_{X,k}$
pour
$M_{X,k+1}=\Pi M_{X,k}+V M_{X,k}$
pour
![]() $k\neq d$
. Quand k vaut d, on en déduit que la famille
$k\neq d$
. Quand k vaut d, on en déduit que la famille
![]() $(\Pi ^i V^{d-i} m_0)_i$
engendre
$(\Pi ^i V^{d-i} m_0)_i$
engendre
et est donc une base par argument de dimension.
Pour terminer la preuve, écrivons
![]() $\Pi ^d m_0=\sum _i a_i x_i$
dans une base
$\Pi ^d m_0=\sum _i a_i x_i$
dans une base
![]() $(x_i)_i$
de
$(x_i)_i$
de
![]() $M_{X,d}$
par des éléments de
$M_{X,d}$
par des éléments de
![]() $M_{X,d}^{V^{-1}\Pi }$
. On obtient alors dans
$M_{X,d}^{V^{-1}\Pi }$
. On obtient alors dans
![]() $M_{X,d}/\varpi M_{X,d}$
:
$M_{X,d}/\varpi M_{X,d}$
:
Le même argument que dans la preuve de 4.1 montre que
![]() $(\Pi ^i V^{d-i} m_0)_i$
est une
$(\Pi ^i V^{d-i} m_0)_i$
est une
![]() $\overline {{\mathbb {F}}}$
-base de
$\overline {{\mathbb {F}}}$
-base de
![]() $M_{X,d}/\varpi M_{X,d}$
si et seulement si
$M_{X,d}/\varpi M_{X,d}$
si et seulement si
![]() $\overline {{\mathbb {F}}}\cdot V^d m_0 \in {\mathbb {P}}^d(\overline {{\mathbb {F}}})\backslash \bigcup _{H\in {\mathbb {P}}^d({\mathbb {F}})}H$
si et seulement si
$\overline {{\mathbb {F}}}\cdot V^d m_0 \in {\mathbb {P}}^d(\overline {{\mathbb {F}}})\backslash \bigcup _{H\in {\mathbb {P}}^d({\mathbb {F}})}H$
si et seulement si
![]() $\overline {{\mathbb {F}}} \cdot \Pi ^d m_0 \in {\mathbb {P}}^d(\overline {{\mathbb {F}}})\backslash \bigcup _{H\in {\mathbb {P}}^d({\mathbb {F}})}H$
.
$\overline {{\mathbb {F}}} \cdot \Pi ^d m_0 \in {\mathbb {P}}^d(\overline {{\mathbb {F}}})\backslash \bigcup _{H\in {\mathbb {P}}^d({\mathbb {F}})}H$
.
Nous appellerons l’isomorphisme précédent morphisme des périodes. Nous pouvons maintenant terminer la preuve du résultat. Reprenons la matrice g construite précédemment ainsi que la droite propre
![]() $\overline {y}\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})$
associée à la valeur propre
$\overline {y}\in {\mathbb {H}}^d_{\overline {{\mathbb {F}}},s}(\overline {{\mathbb {F}}})$
associée à la valeur propre
![]() $\lambda $
. Via l’application des périodes, cette droite détermine un couple
$\lambda $
. Via l’application des périodes, cette droite détermine un couple
![]() $(M_X,\rho )$
pour lequel g agit par multiplication par
$(M_X,\rho )$
pour lequel g agit par multiplication par
![]() $\lambda $
sur
$\lambda $
sur
![]() $D:=\Pi ^d M_{X,0}/ \varpi M_{X,d}$
. En reprenant les arguments de la preuve du lemme précédent, les générateurs de D engendrent
$D:=\Pi ^d M_{X,0}/ \varpi M_{X,d}$
. En reprenant les arguments de la preuve du lemme précédent, les générateurs de D engendrent
![]() $\operatorname {\mathrm {Lie}} (X)_d$
où g agit donc par multiplication par
$\operatorname {\mathrm {Lie}} (X)_d$
où g agit donc par multiplication par
![]() $\lambda $
sur
$\lambda $
sur
![]() $\operatorname {\mathrm {Lie}} (X)_d$
. Comme l’indice d est critique, on a
$\operatorname {\mathrm {Lie}} (X)_d$
. Comme l’indice d est critique, on a
![]() $\operatorname {\mathrm {Lie}} (X)_d =\ker (\Pi : \operatorname {\mathrm {Lie}} (X)_d\to \operatorname {\mathrm {Lie}} (X)_0)$
d’où
$\operatorname {\mathrm {Lie}} (X)_d =\ker (\Pi : \operatorname {\mathrm {Lie}} (X)_d\to \operatorname {\mathrm {Lie}} (X)_0)$
d’où
![]() $[g]_1\cdot T=\lambda ^{-1} T$
sur
$[g]_1\cdot T=\lambda ^{-1} T$
sur
![]() $\pi ^{-1} (\overline {y})$
par dualité. Le résultat s’en déduit.
$\pi ^{-1} (\overline {y})$
par dualité. Le résultat s’en déduit.
6.2 Le tube au-dessus d’une intersection de composantes irréductibles
Le but de ce paragraphe est de démontrer le résultat suivant:
Proposition 6.6. Si
![]() $\sigma $
est un simplexe de dimension non nulle, alors
$\sigma $
est un simplexe de dimension non nulle, alors
![]() ${\mathrm {H}^{j}_{\mathrm { dR},c}(\Sigma ^1_{\operatorname {\mathrm {Ost}}(\sigma )})[\theta ] {\kern-1pt}={\kern-1pt}0}$
pour tout j et tout caractère primitif
${\mathrm {H}^{j}_{\mathrm { dR},c}(\Sigma ^1_{\operatorname {\mathrm {Ost}}(\sigma )})[\theta ] {\kern-1pt}={\kern-1pt}0}$
pour tout j et tout caractère primitif
![]() $\theta $
.
$\theta $
.
En utilisant l’action de G, on peut supposer que
![]() $\sigma $
est un simplexe standard (en particulier, on a
$\sigma $
est un simplexe standard (en particulier, on a
![]() $\sigma =\{[M_i]\}_i$
avec
$\sigma =\{[M_i]\}_i$
avec
![]() $M_0={\mathcal {O}}_K^{d+1}$
), de dimension
$M_0={\mathcal {O}}_K^{d+1}$
), de dimension
![]() $k\geq 1$
et de type
$k\geq 1$
et de type
![]() $(e_0,...,e_k)$
. D’après le théorème 5.1, on dispose d’un isomorphisme naturel
$(e_0,...,e_k)$
. D’après le théorème 5.1, on dispose d’un isomorphisme naturel
 $$\begin{align*}\mathrm{H}^{j}_{\mathrm{dR}} (\Sigma^1_{ \operatorname{\mathrm{Ost}}(\sigma)})[\theta] \cong \mathrm{H}^{j}_{\mathrm{dR}} (\Sigma^1_{ \operatorname{\mathrm{Ost}}(\sigma)} \backslash (\bigcup_{s \notin \sigma} \Sigma^1_{ \operatorname{\mathrm{Ost}}(s)} ))[\theta] \cong \mathrm{H}^{j}_{\mathrm{ dR}} (\Sigma^1_{ \mathring{\sigma}})[\theta]. \end{align*}$$
$$\begin{align*}\mathrm{H}^{j}_{\mathrm{dR}} (\Sigma^1_{ \operatorname{\mathrm{Ost}}(\sigma)})[\theta] \cong \mathrm{H}^{j}_{\mathrm{dR}} (\Sigma^1_{ \operatorname{\mathrm{Ost}}(\sigma)} \backslash (\bigcup_{s \notin \sigma} \Sigma^1_{ \operatorname{\mathrm{Ost}}(s)} ))[\theta] \cong \mathrm{H}^{j}_{\mathrm{ dR}} (\Sigma^1_{ \mathring{\sigma}})[\theta]. \end{align*}$$
On a, d’après le théorème 3.5
avec
![]() $u_1= (-1)^{d}\prod _{a \in ({\mathbb {F}}_q)^{d+1} \backslash \{ 0 \}}\frac {a_0z_0 +\cdots +a_d z_d}{z_d}$
avec
$u_1= (-1)^{d}\prod _{a \in ({\mathbb {F}}_q)^{d+1} \backslash \{ 0 \}}\frac {a_0z_0 +\cdots +a_d z_d}{z_d}$
avec
![]() $z=[z_0,\cdots ,z_d]$
un système de variable sur l’espace projectif
$z=[z_0,\cdots ,z_d]$
un système de variable sur l’espace projectif
![]() ${\mathbb {P}}^d_K$
adapté à
${\mathbb {P}}^d_K$
adapté à
![]() $\sigma $
. Nous souhaitons restreindre le torseur
$\sigma $
. Nous souhaitons restreindre le torseur
![]() $\kappa (\varpi u_1)$
à
$\kappa (\varpi u_1)$
à
![]() ${\mathbb {H}}_{\breve {K}, \mathring {\sigma }}^d$
car
${\mathbb {H}}_{\breve {K}, \mathring {\sigma }}^d$
car
![]() $\Sigma ^1_{ \mathring {\sigma }}\subset \Sigma ^1_{ \operatorname {\mathrm {Ost}}(s)}$
. On rappelle [Reference De Shalit10, 6.4] que cet espace admet une décomposition
$\Sigma ^1_{ \mathring {\sigma }}\subset \Sigma ^1_{ \operatorname {\mathrm {Ost}}(s)}$
. On rappelle [Reference De Shalit10, 6.4] que cet espace admet une décomposition
 $$\begin{align*}{\mathbb{H}}_{\breve{K}, \mathring{\sigma}}^d \cong A_k \times \prod_{i=0}^k C_{e_i-1}\cong A_k \times C_{\sigma}, \end{align*}$$
$$\begin{align*}{\mathbb{H}}_{\breve{K}, \mathring{\sigma}}^d \cong A_k \times \prod_{i=0}^k C_{e_i-1}\cong A_k \times C_{\sigma}, \end{align*}$$
où
![]() $A_k$
et
$A_k$
et
![]() $C_{e_i-1}, C_{\sigma }$
sont les espaces introduits dans le paragraphe 3.3. Nous allons exhiber une décomposition similaire pour les torseurs. Introduisons avant quelques notations. Pour a unimodulaire ie.
$C_{e_i-1}, C_{\sigma }$
sont les espaces introduits dans le paragraphe 3.3. Nous allons exhiber une décomposition similaire pour les torseurs. Introduisons avant quelques notations. Pour a unimodulaire ie.
![]() $a\in M_0\backslash \varpi M_0$
,
$a\in M_0\backslash \varpi M_0$
,
![]() $i(a)$
sera l’unique entier tel que
$i(a)$
sera l’unique entier tel que
![]() $a \in M_{i(a)} \backslash M_{i(a)-1}$
.
$a \in M_{i(a)} \backslash M_{i(a)-1}$
.
Lemme 6.7. Soient S un ensemble fini de vecteur unimodulaire et
![]() $(\alpha _a)_{a\in S}$
des entiers de somme nulleFootnote
17
et soit
$(\alpha _a)_{a\in S}$
des entiers de somme nulleFootnote
17
et soit
![]() $Q=\prod _{a\in S} l_a^{\alpha _a}$
. Notons
$Q=\prod _{a\in S} l_a^{\alpha _a}$
. Notons
Il existe des sections
![]() $Q_{C_{e_i-1}}\in {\mathscr {O}}^{*}(C_{e_i-1})$
, chacune étant un produit homogène de degré
$Q_{C_{e_i-1}}\in {\mathscr {O}}^{*}(C_{e_i-1})$
, chacune étant un produit homogène de degré
![]() $0$
de formes linéaire tel que
$0$
de formes linéaire tel que
avec
![]() $Q_{C_{\sigma }}=Q_{C_{e_0-1}} \dots Q_{C_{e_k-1}} \in {\mathscr {O}}^{*}(C_{\sigma })$
$Q_{C_{\sigma }}=Q_{C_{e_0-1}} \dots Q_{C_{e_k-1}} \in {\mathscr {O}}^{*}(C_{\sigma })$
Démonstration. Il suffit de montrer le résultat pour les fractions de la forme
![]() $\frac {l_a}{z_{d}}$
. On rappelle que l’on a introduit des sous-modules
$\frac {l_a}{z_{d}}$
. On rappelle que l’on a introduit des sous-modules
![]() $N_i\subset M_i$
tels que:
$N_i\subset M_i$
tels que:
 $$\begin{align*}M_k&=N_0\oplus \cdots\oplus N_k\\M_i&=N_0\oplus \cdots\oplus N_i\oplus \varpi N_{i+1}\oplus \cdots\oplus\varpi N_k.\end{align*}$$
$$\begin{align*}M_k&=N_0\oplus \cdots\oplus N_k\\M_i&=N_0\oplus \cdots\oplus N_i\oplus \varpi N_{i+1}\oplus \cdots\oplus\varpi N_k.\end{align*}$$
On peut alors décomposer
![]() $a = a_1 +a_2$
avec
$a = a_1 +a_2$
avec
![]() $a_1$
dans
$a_1$
dans
![]() $N_{i(a)}$
unimodulaire,
$N_{i(a)}$
unimodulaire,
![]() $a_2$
dans
$a_2$
dans
![]() $M_{i(a)-1}$
. On a
$M_{i(a)-1}$
. On a
 $$\begin{align*}\frac{l_a}{z_{d}}= \frac{z_{d_{i(a)}}}{z_{d}} \frac{l_{a_1}+ l_{a_2}}{z_{d_{i(a)}}}=\frac{z_{d_{i(a)}}}{z_{d}} \frac{l_{a_1}}{z_{d_{i(a)}}} (1+ \frac{l_{a_2}}{l_{a_1}}). \end{align*}$$
$$\begin{align*}\frac{l_a}{z_{d}}= \frac{z_{d_{i(a)}}}{z_{d}} \frac{l_{a_1}+ l_{a_2}}{z_{d_{i(a)}}}=\frac{z_{d_{i(a)}}}{z_{d}} \frac{l_{a_1}}{z_{d_{i(a)}}} (1+ \frac{l_{a_2}}{l_{a_1}}). \end{align*}$$
Le terme
![]() $\frac {z_{d_{i(a)}}}{z_{d}}$
est dans
$\frac {z_{d_{i(a)}}}{z_{d}}$
est dans
![]() ${\mathscr {O}}^{*}(A_k)$
, la fraction
${\mathscr {O}}^{*}(A_k)$
, la fraction
![]() $\frac {l_{a_1}}{z_{d_{i(a)}}}$
dans
$\frac {l_{a_1}}{z_{d_{i(a)}}}$
dans
![]() ${\mathscr {O}}^{*}(C_{e_{i}-1})$
(cf 3.1) et
${\mathscr {O}}^{*}(C_{e_{i}-1})$
(cf 3.1) et
![]() $\frac {l_{a_2}}{l_{a_1}}$
dans
$\frac {l_{a_2}}{l_{a_1}}$
dans
![]() ${\mathscr {O}}^{++}({\mathbb {H}}_{\breve {K},\mathring {\sigma }}^d)$
par définition de
${\mathscr {O}}^{++}({\mathbb {H}}_{\breve {K},\mathring {\sigma }}^d)$
par définition de
![]() ${\mathbb {H}}_{\breve {K},\mathring {\sigma }}^d$
. De plus, la fraction
${\mathbb {H}}_{\breve {K},\mathring {\sigma }}^d$
. De plus, la fraction
![]() $Q_{A_k}=\frac {z_{d_{i(a)}}}{z_{d}}$
a la forme voulue ce qui conclut la preuve de l’énoncé.
$Q_{A_k}=\frac {z_{d_{i(a)}}}{z_{d}}$
a la forme voulue ce qui conclut la preuve de l’énoncé.
D’après ce qui précède (et en utilisant le fait que N est premier à p, donc toute fonction f telle que
![]() $|f-1|<1$
est une puissance N-ième), on peut décomposer
$|f-1|<1$
est une puissance N-ième), on peut décomposer
![]() $u_1=u_{A_k}u_{C_{\sigma }} \pmod {{\mathscr {O}}^{*}({\mathbb {H}}_{\breve {K},\mathring {\sigma }}^d)^N}$
. Introduisons les
$u_1=u_{A_k}u_{C_{\sigma }} \pmod {{\mathscr {O}}^{*}({\mathbb {H}}_{\breve {K},\mathring {\sigma }}^d)^N}$
. Introduisons les
![]() $\mu _N$
-revêtements
$\mu _N$
-revêtements
Soit H l’antidiagonale de
![]() $\mu _N^{2}$
. On a
$\mu _N^{2}$
. On a
Lemme 6.8. L’espace
![]() ${\mathcal {T}}_{A_{k}}$
a
${\mathcal {T}}_{A_{k}}$
a
![]() $q^m-1$
composantes géométriques avec
$q^m-1$
composantes géométriques avec
![]() $m=\mathrm { PGCD}(d+1,e_0,\cdots ,e_k)$
.
$m=\mathrm { PGCD}(d+1,e_0,\cdots ,e_k)$
.
Démonstration. Notons que
![]() $A_k$
est un tore monômial semi-ouvert. En effet,
$A_k$
est un tore monômial semi-ouvert. En effet,
et on réalise le changement de variable
![]() $x_0=\frac {y_0}{y_1}$
,
$x_0=\frac {y_0}{y_1}$
,
![]() $x_1=\frac {y_1}{y_2}, \cdots , x_{k-1}={y_{k-1}}$
pour obtenirFootnote
18
$x_1=\frac {y_1}{y_2}, \cdots , x_{k-1}={y_{k-1}}$
pour obtenirFootnote
18
De plus, on a (cf 6.7)
 $$\begin{align*}u_{A_k}=\prod\limits_{{\substack{i=0}}}^{k-1}{(\frac{z_{d_i}}{z_{d}})^{\beta_i}}=\prod\limits_{{\substack{i=0}}}^{k-1}{y_i^{\beta_i}}=\prod\limits_{{\substack{i=0}}}^{k-1}{x_i^{\beta_i+\cdots +\beta_{k-1}}}\end{align*}$$
$$\begin{align*}u_{A_k}=\prod\limits_{{\substack{i=0}}}^{k-1}{(\frac{z_{d_i}}{z_{d}})^{\beta_i}}=\prod\limits_{{\substack{i=0}}}^{k-1}{y_i^{\beta_i}}=\prod\limits_{{\substack{i=0}}}^{k-1}{x_i^{\beta_i+\cdots +\beta_{k-1}}}\end{align*}$$
où
![]() $\beta _i =|(M_i/\varpi M_0)\backslash (M_{i+1}/\varpi M_0)|=q^{d+1-d_{i+1}}(q^{e_i}-1)$
.
$\beta _i =|(M_i/\varpi M_0)\backslash (M_{i+1}/\varpi M_0)|=q^{d+1-d_{i+1}}(q^{e_i}-1)$
.
Le nombre de composantes connexes géométriques
![]() $\pi _0$
de
$\pi _0$
de
![]() ${\mathcal {T}}_{A_{k}}$
est (cf [Reference Junger26, Proposition 4.1.])
${\mathcal {T}}_{A_{k}}$
est (cf [Reference Junger26, Proposition 4.1.])
La partie isotypique en
![]() $\theta $
est donnée par:
$\theta $
est donnée par:
On voit
![]() $\theta $
comme un élément de
$\theta $
comme un élément de
![]() ${\mathbb {Z}}/N{\mathbb {Z}}$
. Le nombre de composantes connexes géométriques de
${\mathbb {Z}}/N{\mathbb {Z}}$
. Le nombre de composantes connexes géométriques de
![]() ${\mathcal {T}}_{A_{k}}$
est de la forme
${\mathcal {T}}_{A_{k}}$
est de la forme
![]() $q^m-1$
et par primitivité de
$q^m-1$
et par primitivité de
![]() $\theta $
,
$\theta $
,
![]() $N/(q^m-1)$
ne divise pas
$N/(q^m-1)$
ne divise pas
![]() $\theta $
dans
$\theta $
dans
![]() ${\mathbb {Z}}/N{\mathbb {Z}}$
. On a alors
${\mathbb {Z}}/N{\mathbb {Z}}$
. On a alors
![]() $\mathrm {H}^{j}_{\mathrm { dR}}({\mathcal {T}}_{A_{k}}) [ \theta ]=0$
d’après 5.11. Ainsi,
$\mathrm {H}^{j}_{\mathrm { dR}}({\mathcal {T}}_{A_{k}}) [ \theta ]=0$
d’après 5.11. Ainsi,
Ce qui conclut la preuve de la proposition 6.6.
6.3 Réalisation de la correspondance de Langlands locale
Dans cette partie, nous allons décrire la cohomologie des espaces
![]() ${\mathcal {M}}_{Dr}^1$
et montrer qu’elle réalise la correspondance de Jacquet-Langlands. On étendra les scalaires à C pour tous les espaces considérés en fibre générique.
${\mathcal {M}}_{Dr}^1$
et montrer qu’elle réalise la correspondance de Jacquet-Langlands. On étendra les scalaires à C pour tous les espaces considérés en fibre générique.
On pourra simplifier le produit
![]() $G \times D^{*} $
en
$G \times D^{*} $
en
![]() $GD$
. On a une ‘valuation’ sur
$GD$
. On a une ‘valuation’ sur
![]() $GD$
:
$GD$
:
On introduit alors pour
![]() $i=0$
ou
$i=0$
ou
![]() $i=d+1$
,
$i=d+1$
,
![]() $[GD]_{i}=v_{GD}^{-1}(i{\mathbb {Z}})$
et
$[GD]_{i}=v_{GD}^{-1}(i{\mathbb {Z}})$
et
![]() $[G]_{i}=G\cap [GD]_{i}$
,
$[G]_{i}=G\cap [GD]_{i}$
,
![]() $[D]_{i}=D^{*}\cap [GD]_{i}$
. Ainsi, on a des inclusions de
$[D]_{i}=D^{*}\cap [GD]_{i}$
. Ainsi, on a des inclusions de
![]() ${\mathcal {O}}_D^{*}$
, G dans
${\mathcal {O}}_D^{*}$
, G dans
![]() $[GD]_0$
$[GD]_0$
 $$\begin{align*}b\in {\mathcal{O}}_D^{*} &\mapsto (Id,b)\in [GD]_0\\g\in G&\mapsto (g, \Pi_D^{- \det(g)})\in [GD]_0 \end{align*}$$
$$\begin{align*}b\in {\mathcal{O}}_D^{*} &\mapsto (Id,b)\in [GD]_0\\g\in G&\mapsto (g, \Pi_D^{- \det(g)})\in [GD]_0 \end{align*}$$
mais les deux sous-groupes ne commutent pas entre eux.
Passons aux représentations qui vont nous intéresser. Nous définissons d’abord des représentations sur
![]() $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}\times {\mathcal {O}}_D^{*} \varpi ^{{\mathbb {Z}}}$
que nous étendrons à
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}\times {\mathcal {O}}_D^{*} \varpi ^{{\mathbb {Z}}}$
que nous étendrons à
![]() $GD$
par induction. Fixons
$GD$
par induction. Fixons
![]() $\theta $
un caractère primitif de
$\theta $
un caractère primitif de
![]() ${\mathbb {F}}_{q^{d+1}}^{*}$
et des isomorphismes
${\mathbb {F}}_{q^{d+1}}^{*}$
et des isomorphismes
![]() $\mathcal{O}_D^*/1+ \Pi_D \mathcal{O}_D \cong \mathbb{F}_{q^{d+1}}^*$
:
$\mathcal{O}_D^*/1+ \Pi_D \mathcal{O}_D \cong \mathbb{F}_{q^{d+1}}^*$
:
-
•
 $\theta $
sera vu comme une
$\theta $
sera vu comme une
 $[D]_{d+1}$
-représentation via
$[D]_{d+1}$
-représentation via
 ${\mathcal {O}}_D^{*} \varpi ^{{\mathbb {Z}}} \to {\mathcal {O}}_D^{*} \to {\mathbb {F}}_{q^{d+1}}^{*}$
,
${\mathcal {O}}_D^{*} \varpi ^{{\mathbb {Z}}} \to {\mathcal {O}}_D^{*} \to {\mathbb {F}}_{q^{d+1}}^{*}$
, -
•
 $\overline {\pi }_{\theta }$
sera la représentation associée à
$\overline {\pi }_{\theta }$
sera la représentation associée à
 $\theta $
sur
$\theta $
sur
 $\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}}_q)$
via la correspondance de Deligne-Lusztig. On la voit comme une
$\operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}}_q)$
via la correspondance de Deligne-Lusztig. On la voit comme une
 $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}$
-représentation via
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}$
-représentation via
 $\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}} \to \operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}}_q)$
.
$\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}} \to \operatorname {\mathrm {GL}}_{d+1}({\mathbb {F}}_q)$
.
Par induction, on obtient:
-
• une représentation
 $\pi (\theta )$
de G, où
$\pi (\theta )$
de G, où
 $\pi (\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}}^G \overline {\pi }_{\theta }$
. Il pourra être utile de considérer
$\pi (\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}}^G \overline {\pi }_{\theta }$
. Il pourra être utile de considérer
 $\tilde {\pi }(\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}}^{[G]_{d+1}} \overline {\pi }_{\theta }$
et d’écrire
$\tilde {\pi }(\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}}^{[G]_{d+1}} \overline {\pi }_{\theta }$
et d’écrire
 $\pi (\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{[G]_{d+1}}^G \tilde {\pi }(\theta )$
,
$\pi (\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{[G]_{d+1}}^G \tilde {\pi }(\theta )$
, -
• une
 $D^{*}$
-représentation
$D^{*}$
-représentation
 $\rho (\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{[D]_{d+1}}^{D^{*}} \theta $
.
$\rho (\theta )= \operatorname {\mathrm {c}-\mathrm {ind}}_{[D]_{d+1}}^{D^{*}} \theta $
.
Nous avons défini une action de
![]() $GD$
sur
$GD$
sur
![]() ${\mathcal {M}}_{Dr}^1$
qui s’identifie non canoniquement à
${\mathcal {M}}_{Dr}^1$
qui s’identifie non canoniquement à
![]() $\Sigma ^1 \times {\mathbb {Z}}$
. Si on confond
$\Sigma ^1 \times {\mathbb {Z}}$
. Si on confond
![]() $\Sigma ^1$
avec
$\Sigma ^1$
avec
![]() $\Sigma ^1 \times \{0 \}\subset {\mathcal {M}}_{Dr}^1/\varpi ^{\mathbb {Z}} \cong \Sigma ^1 \times {\mathbb {Z}}/(d+1){\mathbb {Z}}$
, on obtient une action sur
$\Sigma ^1 \times \{0 \}\subset {\mathcal {M}}_{Dr}^1/\varpi ^{\mathbb {Z}} \cong \Sigma ^1 \times {\mathbb {Z}}/(d+1){\mathbb {Z}}$
, on obtient une action sur
![]() $\Sigma^1$
de son stabilisateur
$\Sigma^1$
de son stabilisateur
![]() $[GD]_{d+1}$
.
$[GD]_{d+1}$
.
Pour énoncer la correspondance de Langlands, nous aurons besoin de la cohomologie de
![]() ${\mathcal {M}}_{Dr}^1$
. On a la relation:
${\mathcal {M}}_{Dr}^1$
. On a la relation:
Nous allons montrer:
Théorème 6.9. Soit
![]() $\theta $
un caractère primitif, on a un isomorphisme G-équivariant:
$\theta $
un caractère primitif, on a un isomorphisme G-équivariant:
 $$\begin{align*}\operatorname{\mathrm{Hom}}_{D^{*}}(\rho(\theta), \mathrm{H}^{i}_{\mathrm{dR},c}(( {\mathcal{M}}_{Dr}^1/ \varpi^{{\mathbb{Z}}})/C)) \underset{G}{\cong} \begin{cases} \pi(\theta)^{d+1} &\text{ si } i=d, \\ 0 &\text{ sinon.} \end{cases} \end{align*}$$
$$\begin{align*}\operatorname{\mathrm{Hom}}_{D^{*}}(\rho(\theta), \mathrm{H}^{i}_{\mathrm{dR},c}(( {\mathcal{M}}_{Dr}^1/ \varpi^{{\mathbb{Z}}})/C)) \underset{G}{\cong} \begin{cases} \pi(\theta)^{d+1} &\text{ si } i=d, \\ 0 &\text{ sinon.} \end{cases} \end{align*}$$
Démonstration. Si
![]() $i \neq d$
, nous avons déjà prouvé l’annulation de la cohomologie. Posons dorénavant
$i \neq d$
, nous avons déjà prouvé l’annulation de la cohomologie. Posons dorénavant
![]() $i=d$
, on a:
$i=d$
, on a:
 $$ \begin{align} \operatorname{\mathrm{Hom}}_{D^{*}}(\rho(\theta), \mathrm{H}^{d}_{\mathrm{dR},c}(( {\mathcal{M}}_{Dr}^1/ \varpi^{{\mathbb{Z}}})/C)) & = \operatorname{\mathrm{Hom}}_{D^{*}} (\operatorname{\mathrm{c}-\mathrm {ind}}_{[D]_{d+1}}^D \theta, \operatorname{\mathrm{c}-\mathrm {ind}}_{[GD]_{d+1}}^{GD} \mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C})) \nonumber\\& = \operatorname{\mathrm{Hom}}_{[D]_{d+1}}(\theta, \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^{G}\mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C}))\nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^{G} \operatorname{\mathrm{Hom}}_{{\mathbb{F}}_{q^{d+1}}^{*}}(\theta, \mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C}))\nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^{G} \mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C}))[\theta]\nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G \pi(\theta) |_{[G]_{d+1}} \\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G \mathrm{res}_{[G]_{d+1}} ( \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G \tilde{\pi}(\theta)) \nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G (\bigoplus_{x \in G/ [G]_{d+1}} c_x(\tilde{\pi}(\theta))) \nonumber\\& = \bigoplus_{x \in G/ [G]_{d+1}}\operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G c_x(\tilde{\pi}(\theta)) \nonumber\\& = \pi(\theta)^{| G / [G]_{d+1} |}= \pi(\theta)^{d+1}.\nonumber \end{align} $$
$$ \begin{align} \operatorname{\mathrm{Hom}}_{D^{*}}(\rho(\theta), \mathrm{H}^{d}_{\mathrm{dR},c}(( {\mathcal{M}}_{Dr}^1/ \varpi^{{\mathbb{Z}}})/C)) & = \operatorname{\mathrm{Hom}}_{D^{*}} (\operatorname{\mathrm{c}-\mathrm {ind}}_{[D]_{d+1}}^D \theta, \operatorname{\mathrm{c}-\mathrm {ind}}_{[GD]_{d+1}}^{GD} \mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C})) \nonumber\\& = \operatorname{\mathrm{Hom}}_{[D]_{d+1}}(\theta, \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^{G}\mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C}))\nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^{G} \operatorname{\mathrm{Hom}}_{{\mathbb{F}}_{q^{d+1}}^{*}}(\theta, \mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C}))\nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^{G} \mathrm{H}^{d}_{\mathrm{dR},c}(\Sigma^1_{C}))[\theta]\nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G \pi(\theta) |_{[G]_{d+1}} \\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G \mathrm{res}_{[G]_{d+1}} ( \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G \tilde{\pi}(\theta)) \nonumber\\& = \operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G (\bigoplus_{x \in G/ [G]_{d+1}} c_x(\tilde{\pi}(\theta))) \nonumber\\& = \bigoplus_{x \in G/ [G]_{d+1}}\operatorname{\mathrm{c}-\mathrm {ind}}_{[G]_{d+1}}^G c_x(\tilde{\pi}(\theta)) \nonumber\\& = \pi(\theta)^{| G / [G]_{d+1} |}= \pi(\theta)^{d+1}.\nonumber \end{align} $$
On rappelle que
![]() $\tilde {\pi }(\theta ) = \operatorname {\mathrm {c}-\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}}^{[G]_{d+1}} \overline {\pi }_{\theta }$
. On a noté
$\tilde {\pi }(\theta ) = \operatorname {\mathrm {c}-\mathrm {ind}}_{\operatorname {\mathrm {GL}}_{d+1}({\mathcal {O}}_K) \varpi ^{{\mathbb {Z}}}}^{[G]_{d+1}} \overline {\pi }_{\theta }$
. On a noté
![]() $c_x(\tilde {\pi }(\theta ))$
la représentation
$c_x(\tilde {\pi }(\theta ))$
la représentation
![]() $ g \mapsto \tilde {\pi }(\theta )(x^{-1}gx)$
. Pour l’avant-dernière égalité, on a utilisé la formule de Mackey
$ g \mapsto \tilde {\pi }(\theta )(x^{-1}gx)$
. Pour l’avant-dernière égalité, on a utilisé la formule de Mackey
![]() $\operatorname {\mathrm {c}-\mathrm {ind}}_{[G]_{d+1}}^G c_x(\tilde {\pi }(\theta ))=\pi (\theta )$
.
$\operatorname {\mathrm {c}-\mathrm {ind}}_{[G]_{d+1}}^G c_x(\tilde {\pi }(\theta ))=\pi (\theta )$
.