Hostname: page-component-f554764f5-c4bhq Total loading time: 0 Render date: 2025-04-10T11:30:01.812Z Has data issue: false hasContentIssue false
  • English
  • Français

BREUIL–KISIN–FARGUES MODULES WITH COMPLEX MULTIPLICATION

Part of: Arithmetic rings and other special rings (Co)homology theory

Published online by Cambridge University Press:  21 January 2020

Johannes Anschütz Open the ORCID record for Johannes Anschütz [Opens in a new window]
Johannes Anschütz*
Affiliation:
Rheinische Friedrich-Wilhelms Universität Bonn, Mathematisches Institut, Bonn, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the category of (rigidified) Breuil–Kisin–Fargues modules up to isogeny is Tannakian. We then introduce and classify Breuil–Kisin–Fargues modules with complex multiplication mimicking the classical theory for rational Hodge structures. In particular, we compute an avatar of a ‘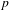$p$-adic Serre group’.

Keywords

p-adic Hodge theorycomplex multiplicationTannakian categorieslocal Galois representations

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology 13F35: Witt vectors and related rings
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 20 , Issue 6 , November 2021 , pp. 1855 - 1904
Check for updates
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abdulali, S., Hodge structures of CM-type, J. Ramunajan Math. Soc. 20 (2006), 155–162.Google Scholar
Anschütz, J., Reductive group schemes over the Fargues–Fontaine curve, Math. Ann. 374(3–4) (2019), 1219–1260.CrossRefGoogle Scholar
Bhatt, B., Morrow, M. and Scholze, P., Integral p-adic Hodge theory, Publ. Math. Inst. Hautes Études Sci. 128 (2018), 219–397.CrossRefGoogle Scholar
Colmez, P. and Fontaine, J.-M., Construction des représentations p-adiques semi-stables, Invent. Math. 140(1) (2000), 1–43.CrossRefGoogle Scholar
Deligne, P., Catégories tannakiennes, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, Volume 87, pp. 111–195 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar
Fargues, L., Motives and automorphic forms: the (potentially) abelian case. Preprint on webpage at https://webusers.imj-prg.fr/∼laurent.fargues/Motifs_abeliens.pdf.Google Scholar
Fargues, L., Quelques résultats et conjectures concernant la courbe, Astérisque 369 (2015), 325–374.Google Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibrés vectoriels en théorie de hodge $p$ -adique. Preprint on webpage at https://webusers.imj-prg.fr/~laurent.fargues/Prepublications.html.Google Scholar
Fargues, L. and Fontaine, J.-M., Courbes et fibrés vectoriels en théorie de Hodge p-adique, Astérisque 406 (2018), xiii+382. With a preface by Pierre Colmez.Google Scholar
Fontaine, J.-M., Modules galoisiens, modules filtrés et anneaux de Barsotti–Tate, in Journées de Géométrie Algébrique de Rennes. (Rennes, 1978), Vol. III, Astérisque, Volume 65, pp. 3–80 (Soc. Math. France, Paris, 1979).Google Scholar
Griffiths, P., Mumford–Tate groups. Preprint on webpage at http://publications.ias.edu/pg/section/155.Google Scholar
Kashiwara, M. and Schapira, P., Categories and Sheaves, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], Volume 332 (Springer, Berlin, 2006).10.1007/3-540-27950-4CrossRefGoogle Scholar
Kisin, M., Crystalline representations and F-crystals, in Algebraic Geometry and Number Theory, Progress in Mathematics, Volume 253, pp. 459–496 (Birkhäuser Boston, Boston, MA, 2006).CrossRefGoogle Scholar
Mocz, L., A new northcott property for faltings height, PhD thesis, Princeton University, ProQuest LLC, Ann Arbor, MI (2018), p. 127.Google Scholar
Saavedra Rivano, N., Catégories Tannakiennes, Lecture Notes in Mathematics, Volume 265 (Springer, Berlin–New York, 1972).Google Scholar
Scholze, P. and Weinstein, J., Lecture notes on $p$ -adic geometry. Available at http://math.bu.edu/people/jsweinst/.Google Scholar
Serre, J.-P., Groupes algébriques associés aux modules de Hodge–Tate, in Journées de Géométrie Algébrique de Rennes. (Rennes, 1978), Vol. III, Astérisque, Volume 65, pp. 155–188 (Soc. Math. France, Paris, 1979).Google Scholar
The Stacks Project Authors, Stacks project. http://stacks.math.columbia.edu, 2017.Google Scholar
Wintenberger, J.-P., Une extension de la théorie de la multiplication complexe, J. Reine Angew. Math. 552 (2002), 1–14.Google Scholar
Wintenberger, J.-P., Propriétés du groupe tannakien des structures de Hodge p-adiques et torseur entre cohomologies cristalline et étale, Ann. Inst. Fourier (Grenoble) 47(5) (1997), 1289–1334.CrossRefGoogle Scholar
Ziegler, P., Graded and filtered fiber functors on Tannakian categories, J. Inst. Math. Jussieu 14(1) (2015), 87–130.CrossRefGoogle Scholar