Article contents
Box splines and the equivariant index theorem
Published online by Cambridge University Press: 01 June 2012
Abstract
In this article, we begin by recalling the inversion formula for the convolution with the box spline. The equivariant cohomology and the equivariant 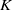 $K$-theory with respect to a compact torus
$K$-theory with respect to a compact torus 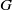 $G$ of various spaces associated to a linear action of
$G$ of various spaces associated to a linear action of 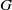 $G$ in a vector space
$G$ in a vector space 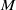 $M$ can both be described using some vector spaces of distributions, on the dual of the group
$M$ can both be described using some vector spaces of distributions, on the dual of the group 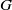 $G$ or on the dual of its Lie algebra
$G$ or on the dual of its Lie algebra 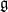 $\mathfrak{g}$. The morphism from
$\mathfrak{g}$. The morphism from 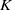 $K$-theory to cohomology is analyzed, and multiplication by the Todd class is shown to correspond to the operator (deconvolution) inverting the semi-discrete convolution with a box spline. Finally, the multiplicities of the index of a
$K$-theory to cohomology is analyzed, and multiplication by the Todd class is shown to correspond to the operator (deconvolution) inverting the semi-discrete convolution with a box spline. Finally, the multiplicities of the index of a 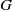 $G$-transversally elliptic operator on
$G$-transversally elliptic operator on 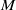 $M$ are determined using the infinitesimal index of the symbol.
$M$ are determined using the infinitesimal index of the symbol.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 3 , July 2013 , pp. 503 - 544
- Copyright
- ©Cambridge University Press 2012
References
- 10
- Cited by


