Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T02:09:43.187Z Has data issue: false hasContentIssue false
  • English
  • Français

A BOUND FOR THE INDEX OF A QUADRATIC FORM AFTER SCALAR EXTENSION TO THE FUNCTION FIELD OF A QUADRIC

Part of: Birational geometry Forms and linear algebraic groups Basic linear algebra

Published online by Cambridge University Press:  16 April 2018

Stephen Scully
Stephen Scully*
Affiliation:
Department of Mathematical and Statistical Sciences, University of Alberta, Edmonton AB T6G 2G1, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $q$ be an anisotropic quadratic form defined over a general field $F$. In this article, we formulate a new upper bound for the isotropy index of $q$ after scalar extension to the function field of an arbitrary quadric. On the one hand, this bound offers a refinement of an important bound established in earlier work of Karpenko–Merkurjev and Totaro; on the other hand, it is a direct generalization of Karpenko’s theorem on the possible values of the first higher isotropy index. We prove its validity in two key cases: (i) the case where 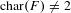$\text{char}(F)\neq 2$, and (ii) the case where 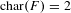$\text{char}(F)=2$ and $q$ is quasilinear (i.e., diagonalizable). The two cases are treated separately using completely different approaches, the first being algebraic–geometric, and the second being purely algebraic.

Keywords

quadratic formsisotropy indicesquadrics and quadratic Grassmanniansrational maps between quadratic Grassmannians

MSC classification

Primary: 11E04: Quadratic forms over general fields 14E05: Rational and birational maps 15A03: Vector spaces, linear dependence, rank
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 421 - 450
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Elman, R., Karpenko, N. and Merkurjev, A., The Algebraic and Geometric Theory of Quadratic Forms, AMS Colloquium Publications, Volume 56 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Fitzgerald, R. W., Function fields of quadratic forms, Math. Z. 178(1) (1981), 63–76.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique (rédigés avec la collaboration de Jean Dieudonné): IV. Étude locale des schémas et des morphismes des schémas, Quatrième partie, Publ. Math. Inst. Hautes Études Sci. 32 (1967), 5–361.Google Scholar
Haution, O., On the first Steenrod square for Chow groups, Amer. J. Math. 135 (2013), 53–63.Google Scholar
Haution, O., Detection by regular schemes in degree two, Algebr. Geom. 2(1) (2015), 44–61.Google Scholar
Hoffmann, D. W., Isotropy of quadratic forms over the function field of a quadric, Math. Z. 220(3) (1995), 461–476.Google Scholar
Hoffmann, D. W., Diagonal forms of degree p in characteristic p, in Algebraic and Arithmetic Theory of Quadratic Forms, Contemporary Mathematics, Volume 344, pp. 135–183 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Hoffmann, D. W. and Laghribi, A., Quadratic forms and Pfister neighbors in characteristic 2, Trans. Amer. Math. Soc. 356(10) (2004), 4019–4053.Google Scholar
Hoffmann, D. W. and Laghribi, A., Isotropy of quadratic forms over the function field of a quadric in characteristic 2, J. Algebra 295(2) (2006), 362–386.Google Scholar
Izhboldin, O., Virtual Pfister neighbors and first Witt index. With an introduction by Nikita Karpenko, in Geometric Methods in the Algebraic Theory of Quadratic Forms, Lecture Notes in Mathematics, Volume 1835, pp. 131–142 (Springer, Berlin, 2004).Google Scholar
Kahn, B., Formes quadratiques sur un corps, Cours Spécialisés, Volume 15 (Société Mathématique de France, Paris, 2008).Google Scholar
Karpenko, N. A., On the first Witt index of quadratic forms, Invent. Math. 153(2) (2003), 455–462.Google Scholar
Karpenko, N. A., Canonical dimension, in Proceedings of the International Congress of Mathematicians, Volume II, pp. 146–161 (Hindustan Book Agency, New Delhi, 2010).Google Scholar
Karpenko, N. A., Upper motives of algebraic groups and incompressibility of Severi–Brauer varieties, J. Reine Angew. Math. 677 (2013), 179–198.Google Scholar
Karpenko, N. and Merkurjev, A., Essential dimension of quadrics, Invent. Math. 153(2) (2003), 361–372.Google Scholar
Knebusch, M., Generic splitting of quadratic forms. I, Proc. Lond. Math. Soc. (3) 33(1) (1976), 65–93.Google Scholar
Knebusch, M., Generic splitting of quadratic forms. II, Proc. Lond. Math. Soc. (3) 34(1) (1977), 1–31.Google Scholar
Laghribi, A., Quasi-hyperbolicity of totally singular quadratic forms, in Algebraic and Arithmetic Theory of Quadratic Forms, Contemporary Mathematics, Volume 344, pp. 237–248 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Rost, M., Some new results on the Chow groups of quadrics. Preprint (1990).Google Scholar
Scully, S., Rational maps between quasilinear hypersurfaces, Compos. Math. 149(3) (2013), 333–355.Google Scholar
Scully, S., On the splitting of quasilinear p-forms, J. Reine Angew. Math. 713 (2016), 49–83.Google Scholar
Scully, S., Hoffmann’s conjecture for totally singular forms of prime degree, Algebra Number Theory 10(5) (2016), 1091–1132.Google Scholar
Scully, S., Hyperbolicity and near hyperbolicity of quadratic forms over function fields of quadrics, Preprint, 2017, arXiv:1609.07100v2, 18 pages.Google Scholar
Totaro, B., Birational geometry of quadrics in characteristic 2, J. Algebraic Geom. 17(3) (2008), 577–597.Google Scholar
Vishik, A., Integral motives of quadrics, MPIM Preprint, 1998-13.Google Scholar
Vishik, A., Direct summands in the motives of quadrics, Preprint, 1999, https://www.maths.nottingham.ac.uk/personal/av/papers.html.Google Scholar
Vishik, A., Motives of quadrics with applications to the theory of quadratic forms, in Geometric Methods in the Algebraic Theory of Quadratic Forms, Lecture Notes in Mathematics, Volume 1835, pp. 25–101 (Springer, Berlin, 2004).Google Scholar
Vishik, A., Excellent connections in the motives of quadrics, Ann. Sci. Éc. Norm. Supér. (4) 44(1) (2011), 183–195.Google Scholar