Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T09:40:46.986Z Has data issue: false hasContentIssue false
  • English
  • Français

BEYOND ENDOSCOPY FOR THE RELATIVE TRACE FORMULA II: GLOBAL THEORY

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  24 April 2017

Yiannis Sakellaridis
Yiannis Sakellaridis*
Affiliation:
Department of Mathematics and Computer Science, Rutgers University at Newark, 101 Warren Street, Smith Hall 216, Newark, NJ 07102, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For the group 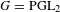$G=\operatorname{PGL}_{2}$ we perform a comparison between two relative trace formulas: on the one hand, the relative trace formula of Jacquet for the quotient 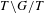$T\backslash G/T$, where $T$ is a nontrivial torus, and on the other the Kuznetsov trace formula (involving Whittaker periods), applied to nonstandard test functions. This gives a new proof of the celebrated result of Waldspurger on toric periods, and suggests a new way of comparing trace formulas, with some analogies to Langlands’ ‘Beyond Endoscopy’ program.

Keywords

relative trace formulabeyond endoscopyperiodsL-functionsWaldspurger’s formula

MSC classification

Primary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 2 , March 2019 , pp. 347 - 447
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altuğ, S. A., Beyond endoscopy via the trace formula: 1. Poisson summation and isolation of special representations, Compos. Math. 151(10) (2015), 1791–1820. doi:10.1112/S0010437X15007320.Google Scholar
Aubert, A.-M. and Plymen, R., Plancherel measure for GL(n, F) and GL(m, D): explicit formulas and Bernstein decomposition, J. Number Theory 112(1) (2005), 26–66. doi:10.1016/j.jnt.2005.01.005.Google Scholar
Bernstein, J. N., On the support of Plancherel measure, J. Geom. Phys. 5(4) (1988), 663–710. doi:10.1016/0393-0440(88)90024-1.Google Scholar
Bernstein, J. and Krötz, B., Smooth Fréchet globalizations of Harish-Chandra modules, Israel J. Math. 199(1) (2014), 45–111. doi:10.1007/s11856-013-0056-1.Google Scholar
Frenkel, E., Langlands, R. and Châu Ngô, B., Formule des traces et fonctorialité: le début d’un programme, Ann. Sci. Math. Québec 34(2) (2010), 199–243.Google Scholar
Gaitsgory, D. and Nadler, D., Spherical varieties and Langlands duality, Mosc. Math. J. 10(1) (2010), 65–137, 271.Google Scholar
Gan, W. T., Gross, B. H. and Prasad, D., Symplectic local root numbers, central critical L values, and restriction problems in the representation theory of classical groups, Astérisque 346 (2012), 1–109. Sur les conjectures de Gross et Prasad. I.Google Scholar
Herman, P. E., Beyond endoscopy for the Rankin-Selberg L-function, J. Number Theory 131(9) (2011), 1691–1722. doi:10.1016/j.jnt.2011.01.019.Google Scholar
Herman, P. E., The functional equation and beyond endoscopy, Pacific J. Math. 260(2) (2012), 497–513. doi:10.2140/pjm.2012.260.497.Google Scholar
Hiraga, K., Ichino, A. and Ikeda, T., Formal degrees and adjoint 𝛾-factors, J. Amer. Math. Soc. 21(1) (2008), 283–304. doi:10.1090/S0894-0347-07-00567-X.Google Scholar
Ichino, A. and Ikeda, T., On the periods of automorphic forms on special orthogonal groups and the Gross–Prasad conjecture, Geom. Funct. Anal. 19(5) (2010), 1378–1425. doi:10.1007/s00039-009-0040-4.Google Scholar
Jacquet, H., Sur un résultat de Waldspurger, Ann. Sci. Éc. Norm. Supér (4) 19(2) (1986), 185–229. URL: http://www.numdam.org/item?id=ASENS_1986_4_19_2_185_0.Google Scholar
Jacquet, H., Sur un résultat de Waldspurger. II, Compos. Math. 63(3) (1987), 315–389. URL: http://www.numdam.org/item?id=CM_1987__63_3_315_0.Google Scholar
Jacquet, H. and Langlands, R. P., Automorphic Forms on GL(2), Lecture Notes in Mathematics, Volume 114 (Springer, Berlin, 1970).Google Scholar
Kottwitz, R. E., Stable trace formula: cuspidal tempered terms, Duke Math. J. 51(3) (1984), 611–650. doi:10.1215/S0012-7094-84-05129-9.Google Scholar
Langlands, R. P., Beyond endoscopy, in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 611–697 (Johns Hopkins University Press, Baltimore, MD, 2004).Google Scholar
Lapid, E. and Mao, Z., A conjecture on Whittaker-Fourier coefficients of cusp forms, J. Number Theory 146 (2015), 448–505. doi:10.1016/j.jnt.2013.10.003.Google Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral Decomposition and Eisenstein Series, Cambridge Tracts in Mathematics, Volume 113 (Cambridge University Press, Cambridge, 1995). Une paraphrase de l’Écriture [A paraphrase of Scripture]. doi:10.1017/CBO9780511470905.Google Scholar
Ono, T., On the Tamagawa number of algebraic tori, Ann. of Math. (2) 78 (1963), 47–73.Google Scholar
Prasad, D., Relating invariant linear form and local epsilon factors via global methods, Duke Math. J. 138(2) (2007), 233–261. With an appendix by Hiroshi Saito. doi:10.1215/S0012-7094-07-13823-7.Google Scholar
Rudnick, Z., Poincaré series, PhD thesis, Yale University (1990).Google Scholar
Saito, H., On Tunnell’s formula for characters of GL(2), Compos. Math. 85(1) (1993), 99–108. URL: http://www.numdam.org/item?id=CM_1993__85_1_99_0.Google Scholar
Sakellaridis, Y., Beyond endoscopy for the relative trace formula I: local theory, in Automorphic Representations and L-functions, Tata Institute of Fundamental Research Studies in Mathematics, Volume 22, pp. 521–590 (Tata Institute of Fundamental Research, Mumbai, 2013).Google Scholar
Sakellaridis, Y., Spherical functions on spherical varieties, Amer. J. Math. 135(5) (2013), 1291–1381. doi:10.1353/ajm.2013.0046.Google Scholar
Sakellaridis, Y., The Schwartz space of a smooth semi-algebraic stack, Selecta Math. (N.S.) 22(4) (2016), 2401–2490. doi:10.1007/s00029-016-0285-3.Google Scholar
Sakellaridis, Y. and Venkatesh, Akshay, Periods and harmonic analysis on spherical varieties. Astérisque, 291pp, to appear, arXiv:1203.0039.Google Scholar
Tunnell, J. B., Local 𝜖-factors and characters of GL(2), Amer. J. Math. 105(6) (1983), 1277–1307. doi:10.2307/2374441.Google Scholar
Venkatesh, A., ‘Beyond endoscopy’ and special forms on GL(2), J. Reine Angew. Math. 577 (2004), 23–80. doi:10.1515/crll.2004.2004.577.23.Google Scholar
Vogan, D. A. Jr., The local Langlands conjecture, in Representation Theory of Groups and Algebras, Contemporary Mathematics, Volume 145, pp. 305–379 (American Mathematical Society, Providence, RI, 1993).Google Scholar
Waldspurger, J.-L., Sur les valeurs de certaines fonctions L automorphes en leur centre de symétrie, Compos. Math. 54(2) (1985), 173–242. URL: http://www.numdam.org/item?id=CM_1985__54_2_173_0.Google Scholar
White, P.-J., The base change L-function for modular forms and Beyond Endoscopy, J. Number Theory 140 (2014), 13–37. doi:10.1016/j.jnt.2014.01.006.Google Scholar
Zhang, W., Automorphic period and the central value of Rankin–Selberg L-function, J. Amer. Math. Soc. 27(2) (2014), 541–612. doi:10.1090/S0894-0347-2014-00784-0.Google Scholar