Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-08T23:19:16.423Z Has data issue: false hasContentIssue false
  • English
  • Français

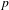BETTI NUMBER ESTIMATES IN $p$-ADIC COHOMOLOGY

Part of: (Co)homology theory

Published online by Cambridge University Press:  07 August 2017

Daniel Caro
Daniel Caro*
Affiliation:
Laboratoire de MathĂ©matiques Nicolas Oresme, UniversitĂ© de Caen Campus 2, 14032 Caen Cedex, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In the framework of Berthelot’s theory of arithmetic 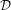${\mathcal{D}}$-modules, we prove the 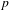$p$-adic analogue of Betti number estimates and we give some standard applications.

Keywords

algebraic geometryp-adic cohomologiesBetti numbersarithmetic 𝓓-modules

MSC classification

Primary: 14F30: $p$-adic cohomology, crystalline cohomology 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 5 , September 2019 , pp. 957 - 991
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, T., Explicit calculation of Frobenius isomorphisms and PoincarĂ© duality in the theory of arithmetic 𝓓-modules, Rend. Semin. Mat. Univ. Padova 131 (2014), 89–149.Google Scholar
Abe, T. and Caro, D., On Beilinson’s equivalence for $p$ -adic cohomology. 09 2013.Google Scholar
Abe, T. and Caro, D., Theory of weights in $p$ -adic cohomology. 03 2013.Google Scholar
Abe, T. and Marmora, A., Product formula for p-adic epsilon factors, J. Inst. Math. Jussieu 14(2) (2015), 275–377.Google Scholar
BeÄ­linson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, in Analysis and Topology on Singular Spaces, I (Luminy 1981), AstĂ©risque, Volume 100, pp. 5–171 (Soc. Math. France, Paris, 1982).Google Scholar
Berthelot, P., Cohomologie rigide et thĂ©orie de Dwork: le cas des sommes exponentielles, AstĂ©risque, (119–120) 3 (1984), 17–49. $p$ -adic cohomology.Google Scholar
Berthelot, P., Cohomologie rigide et thĂ©orie des 𝓓-modules, in p-adic Analysis (Trento, 1989), pp. 80–124 (Springer, Berlin, 1990).Google Scholar
Berthelot, P., AltĂ©rations de variĂ©tĂ©s algĂ©briques (d’aprĂšs A. J. de Jong), AstĂ©risque, (241), Exp. No. 815 5 (1997), 273–311. SĂ©minaire Bourbaki, Vol. 1995/96.Google Scholar
Berthelot, P., 𝓓-modules arithmĂ©tiques. II. Descente par Frobenius, MĂ©m. Soc. Math. Fr. (N.S.) 81 (2000), vi+136.Google Scholar
Berthelot, P., Introduction Ă  la thĂ©orie arithmĂ©tique des 𝓓-modules, AstĂ©risque 279 (2002), 1–80. Cohomologies $p$ -adiques et applications arithmĂ©tiques, II.Google Scholar
Caro, D., Lagrangianity for log extendable overconvergent F-isocrystals, Math. Z. , available online in December 2016, 15 pages.Google Scholar
Caro, D., DĂ©vissages des F-complexes de 𝓓-modules arithmĂ©tiques en F-isocristaux surconvergents, Invent. Math. 166(2) (2006), 397–456.Google Scholar
Caro, D., Fonctions L associĂ©es aux 𝓓-modules arithmĂ©tiques. Cas des courbes, Compos. Math. 142(01) (2006), 169–206.Google Scholar
Caro, D., Overconvergent F-isocrystals and differential overcoherence, Invent. Math. 170(3) (2007), 507–539.Google Scholar
Caro, D. and Tsuzuki, N., Overholonomicity of overconvergent F-isocrystals over smooth varieties, Ann. of Math. (2) 176(2) (2012), 747–813.Google Scholar
Christol, G. and Mebkhout, Z., Sur le thĂ©orĂšme de l’indice des Ă©quations diffĂ©rentielles p-adiques. IV, Invent. Math. 143(3) (2001), 629–672.Google Scholar
Christol, G. and Mebkhout, Z., Sur le thĂ©orĂšme de l’indice des Ă©quations diffĂ©rentielles p-adiques. IV, Invent. Math. 143(3) (2001), 629–672.Google Scholar
Christol, G. and Mebkhout, Z., Équations diffĂ©rentielles p-adiques et coefficients p-adiques sur les courbes, AstĂ©risque 279 (2002), 125–183. Cohomologies $p$ -adiques et applications arithmĂ©tiques, II.Google Scholar
Crew, R., Finiteness theorems for the cohomology of an overconvergent isocrystal on a curve, Ann. Sci. Éc. Norm. SupĂ©r. (4) 31(6) (1998), 717–763.Google Scholar
de Jong, A. J., Smoothness, semi-stability and alterations, Inst. Hautes Études Sci. Publ. Math. 83 (1996), 51–93.Google Scholar
Deligne, P., La conjecture de Weil. II, Inst. Hautes Études Sci. Publ. Math. 52 (1980), 137–252.Google Scholar
Fulton, W., Intersection Theory, second edition, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics], Volume 2 (Springer, Berlin, 1998).Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. I. Le langage des schĂ©mas, Inst. Hautes Études Sci. Publ. Math. 4 (1960), 228.Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. II. Étude globale Ă©lĂ©mentaire de quelques classes de morphismes, Inst. Hautes Études Sci. Publ. Math. 8 (1961), 222.Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. IV. Étude locale des schĂ©mas et des morphismes de schĂ©mas. I, Inst. Hautes Études Sci. Publ. Math. 20 (1964), 259.Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. IV. Étude locale des schĂ©mas et des morphismes de schĂ©mas. II, Inst. Hautes Études Sci. Publ. Math. (24) (1965), 231.Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. IV. Étude locale des schĂ©mas et des morphismes de schĂ©mas. III, Inst. Hautes Études Sci. Publ. Math. (28) (1966), 255.Google Scholar
Grothendieck, A., ÉlĂ©ments de gĂ©omĂ©trie algĂ©brique. IV. Étude locale des schĂ©mas et des morphismes de schĂ©mas IV, Inst. Hautes Études Sci. Publ. Math. (32) (1967), 361.Google Scholar
Katz, N. M. and Laumon, G., Transformation de Fourier et majoration de sommes exponentielles, Inst. Hautes Études Sci. Publ. Math. 62 (1985), 361–418.Google Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals on a curve, Math. Res. Lett. 10(2–3) (2003), 151–159.Google Scholar
Kedlaya, K. S., More Ă©tale covers of affine spaces in positive characteristic, J. Algebraic Geom. 14(1) (2005), 187–192.Google Scholar
Kedlaya, K. S., p-adic Differential Equations, Cambridge Studies in Advanced Mathematics, Volume 125 (Cambridge University Press, Cambridge, 2010).Google Scholar
Kedlaya, K. S., Semistable reduction for overconvergent F-isocrystals, IV: local semistable reduction at nonmonomial valuations, Compos. Math. 147(2) (2011), 467–523.Google Scholar
Lang, S., Algebra, third edition, Graduate Texts in Mathematics, Volume 211 (Springer, New York, 2002).Google Scholar
Laumon, G., Transformations canoniques et spĂ©cialisation pour les rD-modules filtrĂ©s, AstĂ©risque (130) (1985), 56–129. Differential systems and singularities (Luminy, 1983).Google Scholar
Liu, Q., Algebraic Geometry and Arithmetic Curves, Oxford Graduate Texts in Mathematics, Volume 6 (Oxford University Press, Oxford, 2002). Translated from the French by Reinie Erné, Oxford Science Publications.Google Scholar
Monsky, P. and Washnitzer, G., Formal cohomology. I, Ann. of Math. (2) 88 (1968), 181–217.Google Scholar
Noot-Huyghe, C., Transformation de Fourier des 𝓓-modules arithmĂ©tiques. I, in Geometric Aspects of Dwork Theory. Vols I, II, pp. 857–907 (Walter de Gruyter GmbH & Co., KG, Berlin, 2004).Google Scholar
RevĂȘtements Ă©tales et groupe fondamental (SGA 1). Documents MathĂ©matiques (Paris) [Mathematical Documents (Paris)], 3. SociĂ©tĂ© MathĂ©matique de France, Paris, 2003. SĂ©minaire de gĂ©omĂ©trie algĂ©brique du Bois Marie 1960–1961. [Geometric Algebra Seminar of Bois Marie 1960–1961], Directed by A. Grothendieck, With two papers by M. Raynaud, Updated and annotated reprint of the 1971 original [Lecture Notes in Mathematics, 224, Springer, Berlin].Google Scholar
Virrion, A., DualitĂ© locale et holonomie pour les 𝓓-modules arithmĂ©tiques, Bull. Soc. Math. France 128(1) (2000), 1–68.Google Scholar