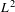Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-04T21:25:31.880Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATION OF $L^{2}$-ANALYTIC TORSION FOR ARITHMETIC QUOTIENTS OF THE SYMMETRIC SPACE 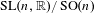$\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$

Part of: Partial differential equations on manifolds; differential operators Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  14 February 2018

Jasmin Matz  and
Werner Müller
Jasmin Matz
Affiliation:
The Hebrew University of Jerusalem, Einstein Institute of Mathematics, Givat Ram, Jerusalem 9190401, Israel ([email protected])
Werner Müller
Affiliation:
Universität Bonn, Mathematisches Institut, Endenicher Allee 60, D – 53115 Bonn, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In [31] we defined a regularized analytic torsion for quotients of the symmetric space 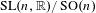$\operatorname{SL}(n,\mathbb{R})/\operatorname{SO}(n)$ by arithmetic lattices. In this paper we study the limiting behavior of the analytic torsion as the lattices run through sequences of congruence subgroups of a fixed arithmetic subgroup. Our main result states that for principal congruence subgroups and strongly acyclic flat bundles, the logarithm of the analytic torsion, divided by the index of the subgroup, converges to the 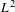$L^{2}$-analytic torsion.

Keywords

analytic torsionlocally symmetric spacestrace formula

MSC classification

Primary: 58J52: Determinants and determinant bundles, analytic torsion
Secondary: 11M36: Selberg zeta functions and regularized determinants; applications to spectral theory, Dirichlet series, Eisenstein series, etc. Explicit formulas
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 307 - 350
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arthur, J., A trace formula for reductive groups. I. Terms associated to classes in G (ℚ), Duke Math. J. 45(4) (1978), 911–952.Google Scholar
Arthur, J., Automorphic representations and number theory, in 1980 Seminar on Harmonic Analysis, Canadian Math. Soc., Conference Proceedings, Volume 1 (AMS, Providence, RI, 1981).Google Scholar
Arthur, J., The trace formula in invariant form, Ann. of Math. (2) 114(1) (1981), 1–74.Google Scholar
Arthur, J., On a family of distributions obtained from Eisenstein series. I. Application of the Paley-Wiener theorem, Amer. J. Math. 104(6) (1982), 1243–1288.Google Scholar
Arthur, J., On a family of distributions obtained from Eisenstein series. II. Explicit formulas, Amer. J. Math. 104(6) (1982), 1289–1336.Google Scholar
Arthur, J., A measure on the unipotent variety, Canad. J. Math. 37(6) (1985), 1237–1274.Google Scholar
Arthur, J., The local behavior of weighted orbital integrals, Duke Math. J. 56(2) (1988), 223–293.Google Scholar
Arthur, J., An introduction to the trace formula, Clay Math. Proc. 4 (2005), 1–263.Google Scholar
Ash, A., Gunnells, P., McConnell, M. and Yasaki, D., On the growth of torsion in the cohomology of arithmetic groups, Preprint, 2016, arXiv:1608.05858.Google Scholar
Barbasch, D. and Moscovici, H., L 2 -index and the trace formula, J. Funct. Anal. 53 (1983), 151–201.Google Scholar
Bergeron, N., Sengün, M. and Venkatesh, A., Torsion homology growth and cycle complexity of arithmetic manifolds, Duke Math. J. 165(9) (2016), 1629–1693.Google Scholar
Bergeron, N. and Venkatesh, A., The asymptotic growth of torsion homology for arithmetic groups, J. Inst. Math. Jussieu 12(2) (2013), 391–447.Google Scholar
Borel, A. and Garland, H., Laplacian and the discrete spectrum of an arithmetic group, Amer. J. Math. 105(2) (1983), 309–335.Google Scholar
Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups, Mathematical Surveys and Monographs, Second edition, Volume 67 (Amer. Math. Soc., Providence, RI, 2000).Google Scholar
Bridson, M. and Haefliger, A., Metric space of non-positive curvature, Grundlehren der Mathematischen Wissenschaften, Volume 319 (Springer, Berlin, 1999).Google Scholar
Clozel, L. and Delorme, P., Le théorème de Paley–Wiener invariant pour les groupes de Lie réductifs, Invent. Math. 77(3) (1984), 427–453.Google Scholar
Collingwood, D. H. and McGovern, W. M., Nilpotent Orbits in Semisimple Lie Algebra (CRC Press, 1993).Google Scholar
Donnelly, H., Stability theorems for the continuous spectrum of a negatively curved manifold, Trans. Amer. Math. Soc. 264(2) (1981), 431–448.Google Scholar
Finis, T. and Lapid, E., On the continuity of the geometric side of the trace formula, Acta Math. Vietnam. 41(3) (2016), 425–455.Google Scholar
Finis, T., Lapid, E. and Müller, W., On the spectral side of Arthur’s trace formula—absolute convergence, Ann. of Math. (2) 174(1) (2011), 173–195.Google Scholar
Finis, T., Lapid, E. and Müller, W., Limit multiplicities for principal congruence subgroups of GL(n) and SL(n), J. Inst. Math. Jussieu 14(3) (2015), 589–638.Google Scholar
Gradshteyn, I. S. and Ryzhik, M. I., Table of Integrals, Series, and Products (Elsevier, Amsterdam, 2007).Google Scholar
Helgason, S., Groups and geometric analysis, in Integral Geometry, Invariant Differential Operators, and Spherical Functions, Pure and Applied Mathematics, Volume 113 (Academic Press, Inc., Orlando, FL, 1984).Google Scholar
Knapp, A. W., Representation Theory of Semisimple Groups (Princeton University Press, Princeton and Oxford, 2001).Google Scholar
Lapid, E. and Müller, W., Spectral asymptotics for arithmetic quotients of SL(n, ℝ)/SO(n), Duke Math. J. 149(1) (2009), 117–155.Google Scholar
Lott, J., Heat kernels on covering spaces and topological invariants, J. Differential Geom. 35(2) (1992), 471–510.Google Scholar
Mathai, V., L 2 -analytic torsion, J. Funct. Anal. 107(2) (1992), 369–386.Google Scholar
Matsushima, Y. and Murakami, S., On vector bundle valued harmonic forms and automorphic forms on symmetric riemannian manifolds, Ann. of Math. (2) 78 (1963), 365–416.Google Scholar
Matz, J., Bounds for global coefficients in the fine geometric expansion of Arthur’s trace formula for GL(n), Israel J. Math. 205(1) (2015), 337–396.Google Scholar
Matz, J., Weyl’s law for Hecke operators on GL(n) over imaginary quadratic number fields, Amer. J. Math. 139(1) (2017), 57–145.Google Scholar
Matz, J. and Müller, W., Analytic torsion of arithmetic quotients of the symmetric space SL(n, ℝ)/SO(n), Geom. Funct. Anal. 27(6) (2017), 1378–1449.Google Scholar
Miatello, R. J., The Minakshisundaram–Pleijel coefficients for the vector-valued heat kernel on compact locally symmetric spaces of negative curvature, Trans. Amer. Math. Soc. 260(1) (1980), 1–33.Google Scholar
Müller, W., Weyl’s law for the cuspidal spectrum of SLn, Ann. of Math. (2) 165 (2007), 275–333.Google Scholar
Müller, W., On the spectral side of the Arthur trace formula, Geom. Funct. Anal. 12(4) (2002), 669–722.Google Scholar
Müller, W. and Pfaff, J., Analytic torsion and L 2 -torsion of compact locally symmetric manifolds, J. Differential Geom. 95(1) (2013), 71–119.Google Scholar
Müller, W. and Speh, B., Absolute convergence of the spectral side of the Arthur trace formula for GL(n), Geom. Funct. Anal. 14(1) (2004), 58–93.Google Scholar
Raimbault, J., Asymptotics of analytic torsion for hyperbolic three–manifolds, Preprint, 2012, arXiv:1212.3161.Google Scholar
Raimbault, J., Analytic, Reidemeister and homological torsion for congruence three–manifolds, Preprint, 2013, arXiv:1307.2845.Google Scholar
Ray, D. B. and Singer, I. M., R-torsion and the Laplacian on Riemannian manifolds, Adv. Math. 7 (1971), 145–210.Google Scholar
Renard, D., Reprśentations des groupes réductifs p-adiques, Cours Spécialisés, Volume 17 (Société Mathématique de France, Paris, 2010).Google Scholar
Shahidi, F., On certain L-functions, Amer. J. Math. 103(2) (1981), 297–355.Google Scholar
Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions, Ann. of Math. (2) 127(3) (1988), 547–584.Google Scholar
Shubin, M. A., Pseudodifferential Operators and Spectral Theory, Second edition (Springer, Berlin, 2001).Google Scholar