Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T01:14:54.697Z Has data issue: false hasContentIssue false
  • English
  • Français

AN EQUIDISTRIBUTION THEOREM FOR HOLOMORPHIC SIEGEL MODULAR FORMS FOR 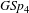$\mathit{GSp}_{4}$ AND ITS APPLICATIONS

Part of: Discontinuous groups and automorphic forms Algebraic number theory: global fields Lie groups

Published online by Cambridge University Press:  22 February 2018

Henry H. Kim ,
Satoshi Wakatsuki  and
Takuya Yamauchi
Henry H. Kim
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 2E4, Canada ([email protected]) Korea Institute for Advanced Study, Seoul, Korea
Satoshi Wakatsuki
Affiliation:
Faculty of Mathematics and Physics, Institute of Science and Engineering, Kanazawa University, Kakumamachi, Kanazawa, Ishikawa, 920-1192, Japan ([email protected])
Takuya Yamauchi
Affiliation:
Mathematical Inst. Tohoku Univ. 6-3, Aoba, Aramaki, Aoba-Ku, Sendai 980-8578, Japan ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove an equidistribution theorem for a family of holomorphic Siegel cusp forms for 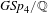$\mathit{GSp}_{4}/\mathbb{Q}$ in various aspects. A main tool is Arthur’s invariant trace formula. While Shin [Automorphic Plancherel density theorem, Israel J. Math.192(1) (2012), 83–120] and Shin–Templier [Sato–Tate theorem for families and low-lying zeros of automorphic $L$-functions, Invent. Math.203(1) (2016) 1–177] used Euler–Poincaré functions at infinity in the formula, we use a pseudo-coefficient of a holomorphic discrete series to extract holomorphic Siegel cusp forms. Then the non-semisimple contributions arise from the geometric side, and this provides new second main terms 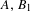$A,B_{1}$ in Theorem 1.1 which have not been studied and a mysterious second term 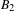$B_{2}$ also appears in the second main term coming from the semisimple elements. Furthermore our explicit study enables us to treat more general aspects in the weight. We also give several applications including the vertical Sato–Tate theorem, the unboundedness of Hecke fields and low-lying zeros for degree 4 spinor $L$-functions and degree 5 standard $L$-functions of holomorphic Siegel cusp forms.

Keywords

trace formulaHecke operatorsSiegel modular forms

MSC classification

Primary: 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms 11F70: Representation-theoretic methods; automorphic representations over local and global fields 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings 11R45: Density theorems
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 351 - 419
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is partially supported by NSERC. The second author is partially supported by JSPS Grant-in-Aid for Scientific Research (nos. 26800006, 25247001, 15K04795). The third author is partially supported by JSPS Grant-in-Aid for Scientific Research (C) no. 15K04787.

References

Arakawa, T., Vector-valued Siegel’s modular forms of degree two and the associated Andrianov L-functions, Manuscripta Math. 44(1–3) (1983), 155–185.Google Scholar
Arthur, J., The L 2 -Lefschetz numbers of Hecke operators, Invent. Math. 97 (1989), 257–290.Google Scholar
Arthur, J., An Introduction to the Trace Formula, Harmonic Analysis, the Trace Formula, and Shimura Varieties, Clay Mathematics Proceedings, Volume 4, pp. 1–263 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Arthur, J., On elliptic tempered characters, Acta Math. 171 (1993), 73–138.Google Scholar
Arthur, J., On the Fourier transforms of weighted orbital integrals, J. Reine Angew. Math. 452 (1994), 163–217.Google Scholar
Arthur, J., Automorphic representations of GSp (4), in Contributions to Automorphic Forms, Geometry, and Number Theory, pp. 65–81 (Johns Hopkins University Press, Baltimore, 2004).Google Scholar
Assem, M., Unipotent orbital integrals of spherical functions on p-adic 4 × 4 symplectic groups, J. Reine Angew. Math. 437 (1993), 181–216.Google Scholar
Borel, A. and Jacquet, H., Automorphic Forms and Automorphic Representations, Proceedings of Symposia in Pure Mathematics, Volume XXXIII, (Part 1) pp. 189–207 (American Mathematical Society, Providence, RI, 1977).Google Scholar
Borel, A. and Wallach, N., Continuous Cohomology, Discrete Subgroups, and Representations of Reductive Groups, second edition, Mathematical Surveys and Monographs, Volume 67 (American Mathematical Society, Providence, RI, 2000).Google Scholar
Bozicević, M., A limit formula for elliptic orbital integrals, Duke Math. J. 113 (2002), 331–353.Google Scholar
Bushnell, C. J. and Henniart, G., An upper bound on conductors for pairs, J. Number Theory 65(2) (1997), 183–196.Google Scholar
Calegari, F. and Gee, T., Irreducibility of automorphic Galois representations, Ann. Inst. Fourier 63(5) (2013), 1881–1912.Google Scholar
Chan, P.-S. and Gan, W. T., The local Langlands conjecture for GSp (4) III: Stability and twisted endoscopy, J. Number Theory 146 (2015), 69–133.Google Scholar
Cho, P. J. and Kim, H. H., Low lying zeros of Artin L-functions, Math. Z. 279 (2015), 669–688.Google Scholar
Cho, P. J. and Kim, H. H., n-level densities of Artin L-functions, Int. Math. Res. Not. IMRN (17) (2015), 7861–7883.Google Scholar
Clozel, L., On limit multiplicities of discrete series representations in spaces of automorphic forms, Invent. Math. 83 (1986), 265–284.Google Scholar
Clozel, L. and Delorme, P., Le theoreme de Paley–Wiener invariant pour les groupes de Lie reductifs II, Ann. Sci. Éc. Norm. Supér. (4) 23 (1990), 193–228.Google Scholar
Dickson, M., Local spectral equidistribution for degree two Siegel modular forms in level and weight aspects, Int. J. Number Theory 11 (2015), 341–396.Google Scholar
Evdokimov, S. A., Euler products for congruence subgroups of the Siegel group of genus 2, Math. USSR Sb. 28 (1976), 431–458.Google Scholar
Ferrari, A., Théorème de l’Indice et Formule des Traces, Manuscripta Math. 124 (2007), 363–390.Google Scholar
Fulton, W. and Harris, J., Representation Theory, A First Course (Springer-Verlag, New York, 1991).Google Scholar
Gan, W. T., The Saito–Kurokawa space of PGSp 4 and its transfer to inner forms, in Eisenstein Series and Applications, Progress in Mathematics, Volume 258, pp. 87–123 (Birkhäuser Boston, 2008).Google Scholar
Gan, W. T. and Takeda, S., The local Langlands conjecture for GSp (4), Ann. of Math. (2) 173(3) (2011), 1841–1882.Google Scholar
Gan, W. T. and Takeda, S., Theta correspondences for GSp(4), Represent. Theory 15 (2011), 670–718.Google Scholar
van der Geer, G., Siegel Modular Forms and their Applications, The 1-2-3 of modular forms, Universitext, pp. 181–245 (Springer, Berlin, 2008).Google Scholar
Hecht, H., The characters of some representations of Harish–Chandra, Math. Ann. 219 (1976), 213–226.Google Scholar
Hiraga, K., On the multiplicities of the discrete series of semisimple Lie groups, Duke Math. J. 85 (1996), 167–181.Google Scholar
Hirai, T., Explicit form of the characters of discrete series representations of semisimple Lie groups, in Harmonic Analysis on Homogeneous Spaces, Proceedings of Symposia in Pure Mathematics, Volume 26, pp. 281–288 (American Mathematical Society, Providence, RI, 1972).Google Scholar
Hoffmann, W. and Wakatsuki, S., On the geometric side of the Arthur trace formula for the symplectic group of rank 2, Mem. Amer. Math. Soc. (to appear).Google Scholar
Ibukiyama, T., Dimension formulas of Siegel modular forms of weight 3 and supersingular abelian varieties, in Proceedings of the 4th Spring Conference on Modular Forms and Related Topics, Siegel Modular Forms and Abelian Varieties (ed. Ibukiyama, T.), pp. 39–60. (2007).Google Scholar
Jiang, D. and Soudry, D., The multiplicity-one theorem for generic automorphic forms on GSp (4), Pacific J. Math. 229 (2007), 381–388.Google Scholar
Katz, N. and Sarnak, P., Random Matrices, Frobenius Eigenvalues and Monodromy, Amer. Math. Soc. Colloq. Publ., Volume 45, pp. 1–427 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Kim, H. H., Residual spectrum of odd orthogonal groups, Int. Math. Res. Not. IMRN (17) (2001), 873–906.Google Scholar
Kim, H. H. and Yamauchi, T., A conditional construction of Artin representations for real analytic Siegel cusp forms of weight (2, 1), in Advances in the Theory of Automorphic Forms and their L-Functions, Contemporary Mathematics, Volume 664, pp. 225–260 (American Mathematical Society, Providence, RI, 2016).Google Scholar
Knapp, A. W., Representation theory of semisimple groups, An overview based on examples, in Reprint of the 1986 original, Princeton Landmarks in Mathematics (Princeton University Press, Princeton, NJ, 2001).Google Scholar
Kowalski, E., Saha, A. and Tsimerman, J., Local spectral equidistribution for Siegel modular forms and applications, Compos. Math. 148 (2012), 335–384.Google Scholar
Langlands, R. P., The dimension of spaces of automorphic forms, Amer. J. Math. 85 (1963), 99–125.Google Scholar
Lansky, J. and Raghuram, A., On the correspondence of reps between GL (n) and division algebras, Proc. Amer. Math. Soc. 131 (2003), 1641–1648.Google Scholar
Laumon, G., Sur la cohomologie a supports compacts des varietes de Shimura pour GSp (4)ℚ, Compos. Math. 105(3) (1997), 267–359.Google Scholar
Laumon, G., Fonctions zetas des varietes de Siegel de dimension trois, Formes automorphes. II. Le cas du groupe GSp(4), Astérisque 302 (2005), 1–66.Google Scholar
Li, X., Upper bounds on L-functions at the edge of the critical strip, Int. Math. Res. Not. IMRN (4) (2010), 727–755.Google Scholar
Luo, W., Rudnick, Z. and Sarnak, P., On the Generalized Ramanujan Conjecture for GL (n), Proceedings of Symposia in Pure Mathematics, Volume 66, pp. 301–310 (American Mathematical Society, Providence, RI, 1999). Part 2.Google Scholar
Martens, S., The characters of the holomorphic discrete series, Proc. Natl. Acad. Sci. USA 72 (1975), 3275–3276.Google Scholar
Marshall, S., Endoscopy and cohomology growth on U (3), Compos. Math. 150 (2014), 903–910.Google Scholar
Miyauchi, M. and Yamauchi, T., An explicit computation of p-stabilized vectors, J. Théor. Nombres Bordeaux 26 (2014), 531–558.Google Scholar
Oda, T., Cohomology of Siegel modular varieties of genus 2 and corresponding automorphic forms, in Geometry and Analysis of Automorphic Forms of Several Variables, pp. 211–253 (World Sci. Publ., Hackensack, NJ, 2012).Google Scholar
Okazaki, T. and Yamauchi, T., On some Siegel threefold related to the tangent cone of the Fermat quartic surface, Adv. Theor. Math. Phys. 21(3) (2017), 585–630.Google Scholar
Piatetski-Shapiro, I. I., On the Saito–Kurokawa lifting, Invent. Math. 71 (1983), 309–338.Google Scholar
Pitale, A., Saha, A. and Schmidt, R., Lowest weight modules of $\mathit{Sp}_{4}(\mathbb{R})$ and nearly holomorphic Siegel modular forms, preprint, arXiv:1501.00524 (2015).Google Scholar
Roberts, B., Global L-packets for GSp (2) and theta lifts, Doc. Math. 6 (2001), 247–314.Google Scholar
Roberts, B. and Schmidt, R., Local Newforms for GSp (4), Lecture Notes in Math. 1918 (2007).Google Scholar
Roberts, B. and Schmidt, R., Some results on Bessel functionals for GSp (4), Doc. Math. 21 (2016), 467–553.Google Scholar
Rossmann, W., Nilpotent Orbital Integrals in a Real Semisimple Lie Algebra and Representations of Weyl Groups, Progress in Mathematics, Volume 92, pp. 263–287 (Birkhäuser, Boston, 1990).Google Scholar
Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory, Duke Math. J. 81 (1996), 269–322.Google Scholar
Salvati Manni, R. and Top, J., Cusp forms of weight 2 for the group 𝛤(4, 8), Amer. J. Math. 115 (1993), 455–486.Google Scholar
Saha, A., On ratios of Petersson norms for Yoshida lifts, Forum Math. 27 (2015), 2361–2412.Google Scholar
Sarnak, P., Statistical properties of eigenvalues of the Hecke operators, in Analytic Number Theory and Diophantine Problems (Stillwater, OK), 1984, Progress in Mathematics, Volume 70, pp. 321–331 (Birkhäuser Boston, Boston, MA, 1987).Google Scholar
Sarnak, P., Shin, S. W. and Templier, N., Families of L-functions and their symmetry, in Families of Automorphic Forms and the Trace Formula. Proceedings of the Simons Symposium, Puerto Rio, pp. 531–578 (Springer, 2016).Google Scholar
Sauvageot, F., Principe de densité pour les groupes réductifs à Solène, pour son premier sourire, Compos. Math. 108 (1997), 151–184.Google Scholar
Schmidt, R., The Saito–Kurokawa lifting and functoriality, Amer. J. Math. 127(1) (2005), 209–240.Google Scholar
Serre, J.-P., Répartition asymptotique des valeurs propres de l’opérateur de Hecke T p, J. Amer. Math. Soc. 10(1) (1997), 75–102.Google Scholar
Shin, S. W., Automorphic Plancherel density theorem, Israel J. Math. 192(1) (2012), 83–120.Google Scholar
Shin, S. W. and Templier, N., Sato-Tate theorem for families and low-lying zeros of automorphic L-functions, Invent. Math. 203(1) (2016), 1–177.Google Scholar
Shin, S. W. and Templier, N., On fields of rationality for automorphic representations, Compos. Math. 150(12) (2014), 2003–2053.Google Scholar
Sorensen, C. M., Galois representations attached to Hilbert–Siegel modular forms, Doc. Math. 15 (2010), 623–670.Google Scholar
Soudry, D., The CAP representations of GSp (4, 𝔸), J. Reine Angew. Math. 383 (1988), 87–108.Google Scholar
Takloo-Bighash, R., Some results on L-functions for the similitude symplectic group of order four GSp (4), in Siavash Shahshahani’s Sixtieth (ed. Lajevardi, K., Safari, P. and Tabesh, Y.), pp. 105–122. (2002).Google Scholar
Taylor, R., On congruences of modular forms, Thesis (1988).Google Scholar
Tsushima, R., An explicit dimension formula for the spaces of generalized automorphic forms with respect to Sp (2, ℤ), Proc. Japan Acad. Ser. A Math. Sci. 59(4) (1983), 139–142.Google Scholar
Wakatsuki, S., Dimension formulas for spaces of vector-valued Siegel cusp forms of degree two, J. Number Theory 132 (2012), 200–253.Google Scholar
Wakatsuki, S., Multiplicity formulas for discrete series representations in L 2(𝛤\Sp(2, ℝ)), J. Number Theory 133 (2013), 3394–3425.Google Scholar
Wallach, N. R., On the constant term of a square integrable automorphic form, Operator Algebras and Group Representations, Vol. II (Neptun, 1980), Monogr. Stud. Math., Volume 18, pp. 227–237 (Pitman, Boston, MA, 1984).Google Scholar
Wang, S., An effective version of the Grunwald–Wang theorem, Thesis at Caltech (2002).Google Scholar
Weissauer, R., On the cohomology of Siegel modular threefolds, in Arithmetic of Complex Manifolds, Lecture Notes in Mathematics, Volume 1399, pp. 155–171 (Springer, Berlin, 1989).Google Scholar
Weissauer, R., Modular forms of genus 2 and weight 1, Math. Z. 210 (1992), 91–96.Google Scholar