No CrossRef data available.
Published online by Cambridge University Press: 07 March 2024
For a real number 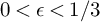 $0<\epsilon <1/3$, we show that the anti-canonical volume of an
$0<\epsilon <1/3$, we show that the anti-canonical volume of an  $\epsilon $-klt Fano
$\epsilon $-klt Fano 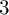 $3$-fold is at most
$3$-fold is at most 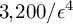 $3,200/\epsilon ^4$, and the order
$3,200/\epsilon ^4$, and the order 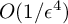 $O(1/\epsilon ^4)$ is sharp.
$O(1/\epsilon ^4)$ is sharp.