Article contents
Algebraic and analytic Dirac induction for graded affine Hecke algebras
Published online by Cambridge University Press: 13 March 2013
Abstract
We define the algebraic Dirac induction map 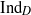 ${\mathrm{Ind} }_{D} $ for graded affine Hecke algebras. The map
${\mathrm{Ind} }_{D} $ for graded affine Hecke algebras. The map 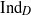 ${\mathrm{Ind} }_{D} $ is a Hecke algebra analog of the explicit realization of the
Baum–Connes assembly map in the
${\mathrm{Ind} }_{D} $ is a Hecke algebra analog of the explicit realization of the
Baum–Connes assembly map in the 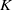 $K$-theory of the reduced
$K$-theory of the reduced 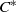 ${C}^{\ast } $-algebra of a real reductive group using Dirac operators. The
definition of
${C}^{\ast } $-algebra of a real reductive group using Dirac operators. The
definition of 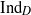 ${\mathrm{Ind} }_{D} $ is uniform over the parameter space of the graded affine Hecke
algebra. We show that the map
${\mathrm{Ind} }_{D} $ is uniform over the parameter space of the graded affine Hecke
algebra. We show that the map 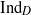 ${\mathrm{Ind} }_{D} $ defines an isometric isomorphism from the space of elliptic
characters of the Weyl group (relative to its reflection representation) to the space
of elliptic characters of the graded affine Hecke algebra. We also study a related
analytically defined global elliptic Dirac operator between unitary representations
of the graded affine Hecke algebra which are realized in the spaces of sections of
vector bundles associated to certain representations of the pin cover of the Weyl
group. In this way we realize all irreducible discrete series modules of the Hecke
algebra in the kernels (and indices) of such analytic Dirac operators. This can be
viewed as a graded affine Hecke algebra analog of the construction of the discrete
series representations of semisimple Lie groups due to Parthasarathy and to Atiyah
and Schmid.
${\mathrm{Ind} }_{D} $ defines an isometric isomorphism from the space of elliptic
characters of the Weyl group (relative to its reflection representation) to the space
of elliptic characters of the graded affine Hecke algebra. We also study a related
analytically defined global elliptic Dirac operator between unitary representations
of the graded affine Hecke algebra which are realized in the spaces of sections of
vector bundles associated to certain representations of the pin cover of the Weyl
group. In this way we realize all irreducible discrete series modules of the Hecke
algebra in the kernels (and indices) of such analytic Dirac operators. This can be
viewed as a graded affine Hecke algebra analog of the construction of the discrete
series representations of semisimple Lie groups due to Parthasarathy and to Atiyah
and Schmid.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 3 , July 2014 , pp. 447 - 486
- Copyright
- ©Cambridge University Press 2013
References
- 13
- Cited by


