Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T03:51:25.820Z Has data issue: false hasContentIssue false
  • English
  • Français

AFFINE GEOMETRY OF STRATA OF DIFFERENTIALS

Part of: Birational geometry Curves

Published online by Cambridge University Press:  26 October 2017

Dawei Chen
Dawei Chen*
Affiliation:
Department of Mathematics, Boston College, Chestnut Hill, MA 02467, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Affine varieties among all algebraic varieties have simple structures. For example, an affine variety does not contain any complete algebraic curve. In this paper, we study affine-related properties of strata of 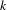$k$-differentials on smooth curves which parameterize sections of the 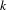$k$th power of the canonical line bundle with prescribed orders of zeros and poles. We show that if there is a prescribed pole of order at least 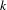$k$, then the corresponding stratum does not contain any complete curve. Moreover, we explore the amusing question whether affine invariant manifolds arising from Teichmüller dynamics are affine varieties, and confirm the answer for Teichmüller curves, Hurwitz spaces of torus coverings, hyperelliptic strata as well as some low genus strata.

Keywords

strata of differentialsmoduli space of curvescomplete curvesaffine varietiesaffine invariant manifolds

MSC classification

Primary: 14H10: Families, moduli (algebraic) 14H15: Families, moduli (analytic) 14E99: None of the above, but in this section
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 6 , November 2019 , pp. 1331 - 1340
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is partially supported by NSF CAREER Award DMS-1350396.

References

Arbarello, E. and Mondello, G., Two remarks on the Weierstrass flag, Contemp. Math. 564 (2012), 137–144.Google Scholar
Bainbridge, M., Chen, D., Gendron, Q., Grushevsky, S. and Möller, M., Compactification of strata of abelian differentials, preprint, 2016, arXiv:1604.08834.Google Scholar
Bainbridge, M., Chen, D., Gendron, Q., Grushevsky, S. and Möller, M., Strata of $k$ -differentials, preprint, 2016, arXiv:1610.09238.Google Scholar
Barros, I., Uniruledness of strata of holomorphic differentials in small genus, preprint, 2017, arXiv:1702.06716.Google Scholar
Chen, D., Teichmüller dynamics in the eyes of an algebraic geometer, preprint, 2016, arXiv:1602.02260.Google Scholar
Chen, D. and Coskun, I., Extremal effective divisors on 𝓜 1, n , Math. Ann. 359(3–4) (2014), 891–908.Google Scholar
Chen, D. and Möller, M., Nonvarying sums of Lyapunov exponents of Abelian differentials in low genus, Geom. Topol. 16(4) (2012), 2427–2479.Google Scholar
Chen, D. and Möller, M., Quadratic differentials in low genus: exceptional and non-varying strata, Ann. Sci. Éc. Norm. Supér. (4) 47(2) (2014), 309–369.Google Scholar
Diaz, S., A bound on the dimensions of complete subvarieties of 𝓜g , Duke Math. J. 51(2) (1984), 405–408.Google Scholar
Eskin, A., Kontsevich, M. and Zorich, A., Sum of Lyapunov exponents of the Hodge bundle with respect to the Teichmüller geodesic flow, Publ. Math. Inst. Hautes Études Sci. 120 (2014), 207–333.Google Scholar
Eskin, A. and Mirzakhani, M., Invariant and stationary measures for the $\text{SL}(2,\mathbb{R})$ action on Moduli space, preprint, 2013, arXiv:1302.3320.Google Scholar
Eskin, A., Mirzakhani, M. and Mohammadi, A., Isolation, equidistribution, and orbit closures for the SL(2, ℝ) action on moduli space, Ann. of Math. (2) 182(2) (2015), 673–721.Google Scholar
Farkas, G. and Pandharipande, R., The moduli space of twisted canonical divisors, with an appendix by F. Janda, R. Pandharipande, A. Pixton, and D. Zvonkine, J. Inst. Math. Jussieu (2016), 1–58, doi:10.1017/S1474748016000128.Google Scholar
Filip, S., Splitting mixed Hodge structures over affine invariant manifolds, Ann. of Math. (2) 183 (2016), 681–713.Google Scholar
Fontanari, C., Moduli of curves via algebraic geometry, Rend. Semin. Mat. Univ. Politec. Torino 59(2) (2001), 137–139.Google Scholar
Fontanari, C. and Looijenga, E., A perfect stratification of 𝓜g for g⩽5, Geom. Dedicata 136 (2008), 133–143.Google Scholar
Gendron, Q., The Deligne-Mumford and the incidence variety compactifications of the strata of $\unicode[STIX]{x1D6FA}{\mathcal{M}}_{g}$ , preprint, 2015, arXiv:1503.03338.Google Scholar
Grushevsky, S. and Krichever, I., The universal Whitham hierarchy and the geometry of the moduli space of pointed Riemann surfaces, Surv. Differ. Geom. 14 (2009), 111–129.Google Scholar
Harris, J., Families of smooth curves, Duke Math. J. 51(2) (1984), 409–419.Google Scholar
Harris, J. and Morrison, I., Moduli of curves, in Graduate Texts in Mathematics, Volume 187 (Springer, New York, 1998).Google Scholar
Hartshorne, R., Ample subvarieties of algebraic varieties, in Lecture Notes in Mathematics, Volume 156 (Springer, Berlin–New York, 1970).Google Scholar
Kontsevich, M. and Zorich, A., Connected components of the moduli spaces of abelian differentials with prescribed singularities, Invent. Math. 153(3) (2003), 631–678.Google Scholar
Looijenga, E., On the tautological ring of 𝓜g , Invent. Math. 121(2) (1995), 411–419.Google Scholar
Looijenga, E. and Mondello, G., The fine structure of the moduli space of abelian differentials in genus 3, Geom. Dedicata 169 (2014), 109–128.Google Scholar
McMullen, C., Mukamel, R. and Wright, A., Cubic curves and totally geodesic subvarieties of moduli space, Ann. Math. 185(3) (2017), 957–990.Google Scholar
Mondello, G., Stratifications of the moduli space of curves and related questions, Rend. Mat. Appl. (7) 35(3–4) (2014), 131–157.Google Scholar
Mumford, D., The red book of varieties and schemes, in Lecture Notes in Mathematics, Volume 1358 (Springer, Berlin, 1988).Google Scholar
Wright, A., Translation surfaces and their orbit closures: an introduction for a broad audience, EMS Surv. Math. Sci. 2 (2015), 63–108.Google Scholar
Zorich, A., Flat surfaces, in Frontiers in Number Theory, Physics, and Geometry I, pp. 437–583 (Springer, Berlin, 2006).Google Scholar