Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-04T19:03:03.808Z Has data issue: false hasContentIssue false
  • English
  • Français

ADJOINT FUNCTORS ON THE DERIVED CATEGORY OF MOTIVES

Part of: Cycles and subschemes (Co)homology theory Abelian categories

Published online by Cambridge University Press:  22 March 2016

Burt Totaro
Burt Totaro*
Affiliation:
UCLA Mathematics Department, Box 951555, Los Angeles, CA 90095-1555, USA ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that the subcategory of mixed Tate motives in Voevodsky’s derived category of motives is not closed under infinite products. In fact, the infinite product 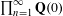$\prod _{n=1}^{\infty }\mathbf{Q}(0)$ is not mixed Tate. More generally, the inclusions of several subcategories of motives do not have left or right adjoints. The proofs use the failure of finite generation for Chow groups in various contexts. In the positive direction, we show that for any scheme of finite type over a field whose motive is mixed Tate, the Chow groups are finitely generated.

Keywords

derived category of motivesChow groupmotivic cohomologymixed Tate motiveadjoint functor

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 14C15: (Equivariant) Chow groups and rings; motives 18E30: Derived categories, triangulated categories
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 3 , June 2018 , pp. 489 - 507
Copyright
© Cambridge University Press 2016 

References

Auel, A., Colliot-Thélène, J.-L. and Parimala, R., Universal unramified cohomology of cubic fourfolds containing a plane, Brauer groups and obstruction problems (Palo Alto, 2013). to appear. arXiv:1310.6705.Google Scholar
Ayoub, J. and Barbieri-Viale, L., 1-motivic sheaves and the Albanese functor, J. Pure Appl. Algebra 213 (2009), 809–839.Google Scholar
Balmer, P., Dell’Ambrogio, I. and Sanders, B., Grothendieck-Neeman duality and the Wirthmüller isomorphism, Compos. Math. to appear.Google Scholar
Bökstedt, M. and Neeman, A., Homotopy limits in triangulated categories, Compos. Math. 86 (1993), 209–234.Google Scholar
Cisinski, D.-C. and Déglise, F., Local and stable homological algebra in Grothendieck abelian categories, Homology, Homotopy Appl. 11 (2009), 219–260.Google Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives. arXiv:0912.2110.Google Scholar
Cisinski, D.-C. and Déglise, F., Integral mixed motives in equal characteristic, (extra volume: Alexander S. Merkurjev’s sixtieth birthday), Doc. Math. (2015), 145–194.Google Scholar
Dugger, D. and Isaksen, D., Motivic cell structures, Algebr. Geom. Topol. 5 (2005), 615–652.Google Scholar
Frey, G. and Jarden, M., Approximation theory and the rank of abelian varieties over large algebraic fields, Proc. Lond. Math. Soc. 28 (1974), 112–128.Google Scholar
Geisser, T., Tate’s conjecture, algebraic cycles and rational K-theory in characteristic p , K-Theory 13 (1998), 109–122.Google Scholar
Huber, A., Slice filtration on motives and the Hodge conjecture (with an appendix by J. Ayoub), Math. Nachr. 281 (2008), 1764–1776.Google Scholar
Huber, A. and Kahn, B., The slice filtration and mixed Tate motives, Compos. Math. 142 (2006), 907–936.Google Scholar
Kelly, S., Triangulated categories of motives in positive characteristic. arXiv:1305.5349.Google Scholar
Neeman, A., The connection between the K-theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel, Ann. Sci. Éc. Norm. Supér. 25 (1992), 547–566.CrossRefGoogle Scholar
Neeman, A., The Grothendieck duality theorem via Bousfield’s techniques and Brown representability, J. Amer. Math. Soc. 9 (1996), 205–236.Google Scholar
Neeman, A., Triangulated categories, Annals of Mathematics Studies, Volume 148 (Princeton University Press, 2001).CrossRefGoogle Scholar
Quillen, D., On the cohomology and K-theory of the general linear groups over a finite field, Ann. of Math. (2) 96 (1972), 552–586.CrossRefGoogle Scholar
Röndigs, O. and Østvær, P., Modules over motivic cohomology, Adv. Math. 219 (2008), 689–727.Google Scholar
Rosenschon, A. and Srinivas, V., The Griffiths group of the generic abelian 3-fold, in Cycles, motives and Shimura varieties, pp. 449–467 (Tata Inst. Fund. Res., Mumbai, 2010).Google Scholar
Schoen, C., Complex multiplication cycles on elliptic modular threefolds, Duke Math. J. 53 (1986), 771–794.CrossRefGoogle Scholar
Schoen, C., Complex varieties for which the Chow group mod n is not finite, J. Algebraic Geom. 11 (2002), 41–100.CrossRefGoogle Scholar
Suslin, A., Algebraic K-theory of fields, Proceedings of the International Congress of Mathematicians (Berkeley, 1986), Volume 1, pp. 222–244 (Amer. Math. Soc., 1987).Google Scholar
Suslin, A., Higher Chow groups and motivic cohomology, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, Volume 143, pp. 239–254 (Princeton University Press, 2000).Google Scholar
Totaro, B., Chow groups, Chow cohomology, and linear varieties, Forum Math. Sigma 2 (2014), e17 (25 pages).Google Scholar
Totaro, B., The motive of a classifying space, Geom. Topol. to appear.Google Scholar
Totaro, B., Complex varieties with infinite Chow groups modulo 2, Ann. of Math. (2) 183 (2016), 363–375.Google Scholar
Voevodsky, V., Triangulated categories of motives over a field, in Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, Volume 143, pp. 188–238 (Princeton University Press, 2000).Google Scholar