Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-09T16:32:31.984Z Has data issue: false hasContentIssue false
  • English
  • Français

Solvable points on genus-one curves over local fields

Published online by Cambridge University Press:  16 May 2012

Ambrus Pál
Ambrus Pál*
Affiliation:
Department of Mathematics, 180 Queen’s Gate, Imperial College, London SW7 2AZ, UK([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 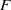be a field complete with respect to a discrete valuation whose residue field is perfect of characteristic 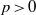. We prove that every smooth, projective, geometrically irreducible curve of genus one defined over 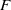with a non-zero divisor of degree a power of 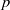has a solvable point over .

Keywords

solvable pointsgenus one curveslocal fields14G0511G07
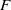Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 12 , Issue 1 , January 2013 , pp. 31 - 42
Copyright
Copyright © Cambridge University Press 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Çiperiani, M. and Wiles, A. , Solvable points on genus one curves, Duke Math. J. 142 (2008), 381–464.Google Scholar
2.Gorenstein, D. , Finite groups, 2nd edn (American Mathematical Society, Providence, Rhode Island, 2007).Google Scholar
3.Grothendieck, A. and Raynaud, M. , Modèles de Néron et monodromie, Groupes de monodromie en Géometrie Algebrique, I, II, Lecture Notes in Math., Volume 288. pp. 313–523 (Springer, 1972).Google Scholar
4.Károlyi, Gy. and Pál, A. , The cyclomatic number of connected graphs without solvable orbits, J. Ramanujan Math. Soc. (2012), in press.Google Scholar
5.Mazur, B. and Roberts, L. , Local Euler characteristics, Invent. Math. 9 (1970), 201–223.CrossRefGoogle Scholar
6.Milne, J. , Étale cohomology (Princeton University Press, Princeton, New Jersey, 1980).Google Scholar
7.Oort, F. and Tate, J. , Group schemes of prime order, Ann. Sci. Éc. Norm . Supér. (4) 3 (1970), 1–21.Google Scholar
8.Pál, A. , Solvable points on projective algebraic curves, Canad. J. Math. 56 (2004), 612–637.Google Scholar
9.Pál, A. , Curves which do not become semi-stable after any solvable extension, Rend. Semin. Mat. Univ. Padova (2012), in press.Google Scholar
10.Roberts, L. , The flat cohomology of group schemes of rank , Amer. J. Math. 95 (1973), 688–702.CrossRefGoogle Scholar
11.Serre, J.-P. , Local fields. GTM 67 (second corrected printing, 1995) (Springer-Verlag, New York–Berlin, 1979).Google Scholar
12.Tate, J. , Finite flat group schemes, Modular forms and Fermats last theorem (Boston, MA, 1995), pp. 121–154 (Springer-Verlag, Berlin–Heidelberg–New York, 1997).Google Scholar