Hostname: page-component-6bf8c574d5-mcfzb Total loading time: 0 Render date: 2025-03-07T13:10:15.787Z Has data issue: false hasContentIssue false
  • English
  • Français

THE PRO-p-IWAHORI HECKE ALGEBRA OF A REDUCTIVE p-ADIC GROUP III (SPHERICAL HECKE ALGEBRAS AND SUPERSINGULAR MODULES)

Part of: Representation theory of groups Lie groups

Published online by Cambridge University Press:  03 June 2015

Marie-France Vigneras
Marie-France Vigneras*
Affiliation:
UMR 7586, Institut de Mathematiques de Jussieu, 4 place Jussieu, Paris 75005, France ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

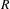Let $R$ be a large field of characteristic 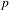$p$. We classify the supersingular simple modules of the pro-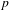$p$-Iwahori Hecke 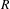$R$-algebra 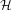${\mathcal{H}}$ of a general reductive 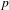$p$-adic group 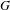$G$. We show that the functor of pro-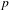$p$-Iwahori invariants behaves well when restricted to the representations compactly induced from an irreducible smooth 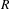$R$-representation $\unicode[STIX]{x1D70C}$ of a special parahoric subgroup 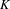$K$ of 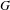$G$. We give an almost-isomorphism between the center of 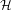${\mathcal{H}}$ and the center of the spherical Hecke algebra 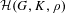${\mathcal{H}}(G,K,\unicode[STIX]{x1D70C})$, and a Satake-type isomorphism for 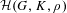${\mathcal{H}}(G,K,\unicode[STIX]{x1D70C})$. This generalizes results obtained by Ollivier for 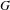$G$ split and 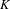$K$ hyperspecial to 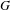$G$ general and 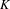$K$ special.

Keywords

group theory and generalizationsnumber theory

MSC classification

Primary: 20C08: Hecke algebras and their representations
Secondary: 22E50: Representations of Lie and linear algebraic groups over local fields
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 16 , Issue 3 , June 2017 , pp. 571 - 608
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N., Henniart, G., Herzig, F. and Vignéras, M.-F., A classification of admissible irreducible modulo $p$ representations of reductive $p$ -adic groups, preprint, 2014.Google Scholar
Cabanes, M., Irreducible modules and Levi supplements, J. Algebra 90 (1984), 84–97.Google Scholar
Cabanes, M., A criterion of complete reducibility and some applications, in Représentations linéeaires des groupes finis, (ed. Cabanes, M.), Astérisque, pp. 181–182. (1990) 93–112.Google Scholar
Cabanes, M. and Enguehard, M., Representation theory of finite reductive groups (Cambridge University Press, 2004).Google Scholar
Grosse-Klönne, E., From pro- $p$ -Iwahori Hecke modules to $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D6E4})$ -modules, preprint, 2013.Google Scholar
Henniart, G. and Vigneras, M.-F., Comparison of compact induction with parabolic induction, Pac. J. Math. 260(2) (2012), 457–495.Google Scholar
Henniart, G. and Vigneras, M.-F., A Satake isomorphism for representations modulo p of reductive groups over local fields, J. Reine Angew. Math. 701 (2015), 33–75.Google Scholar
Kumar, S., Kac–Moody groups, their flag varieties and representation theory, Progr. Math. 204 (2002).Google Scholar
Ollivier, R., Parabolic Induction and Hecke modules in characteristic p for p-adic GL n , ANT 4(6) (2010), 701–742.Google Scholar
Ollivier, R., An Inverse Satake isomorphism in characteristic $p$ , Selecta Math., preprint, 2012.Google Scholar
Ollivier, R., Compatibility between Satake and Bernstein isomorphisms in characteristic $p$ , preprint, 2013.Google Scholar
Schmidt, N. A., Generische pro-p-algebren (Dilpomarbeit, Berlin, 2009).Google Scholar
Vignéras, M.-F., On a numerical Langlands correspondence modulo p with the pro-p-Iwahori Hecke ring, Math. Ann. 331(3) 1432–1807. Erratum 333(3) (2005), 699–701.Google Scholar
Vignéras, M.-F., Algèbres de Hecke affines génériques, J. Represent. Theory 10 (2006), 1–20.CrossRefGoogle Scholar
Vignéras, M.-F., The pro- $p$ -Iwahori Hecke algebra of a reductive $p$ -adic group I, preprint, 2013.Google Scholar
Vignéras, M.-F., The pro-p-Iwahori Hecke algebra of a reductive p-adic group II, Muenster J. Math. 7 (2014), 363–379.Google Scholar