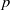Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-17T19:06:29.722Z Has data issue: false hasContentIssue false
  • English
  • Français

Pro-$\lowercase p$ Iwahori–Hecke algebras are Gorenstein

Part of: Representation theory of groups Homological methods

Published online by Cambridge University Press:  28 November 2013

Rachel Ollivier  and
Peter Schneider
Rachel Ollivier
Affiliation:
Columbia University, Department of Mathematics, 2990 Broadway, New York, NY 10027, USA ([email protected])
Peter Schneider
Affiliation:
Universität Münster, Mathematisches Institut, Einsteinstr. 62, 48291 Münster, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 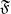$\mathfrak{F}$ be a locally compact nonarchimedean field with residue characteristic 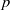$p$, and let 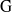$\mathrm{G} $ be the group of 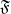$\mathfrak{F}$-rational points of a connected split reductive group over 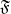$\mathfrak{F}$. For 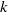$k$ an arbitrary field of any characteristic, we study the homological properties of the Iwahori–Hecke 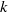$k$-algebra ${\mathrm{H} }^{\prime } $ and of the pro-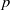$p$ Iwahori–Hecke 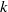$k$-algebra 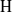$\mathrm{H} $ of 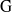$\mathrm{G} $. We prove that both of these algebras are Gorenstein rings with self-injective dimension bounded above by the rank of 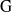$\mathrm{G} $. If 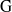$\mathrm{G} $ is semisimple, we also show that this upper bound is sharp, that both 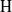$\mathrm{H} $ and 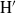${\mathrm{H} }^{\prime } $ are Auslander–Gorenstein, and that there is a duality functor on the finite length modules of 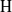$\mathrm{H} $ (respectively 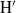${\mathrm{H} }^{\prime } $). We obtain the analogous Gorenstein and Auslander–Gorenstein properties for the graded rings associated to 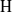$\mathrm{H} $ and 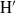${\mathrm{H} }^{\prime } $.

When 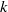$k$ has characteristic 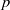$p$, we prove that in ‘most’ cases 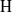$\mathrm{H} $ and 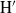${\mathrm{H} }^{\prime } $ have infinite global dimension. In particular, we deduce that the category of smooth 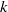$k$-representations of 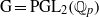$\mathrm{G} = {\mathrm{PGL} }_{2} ({ \mathbb{Q} }_{p} )$ generated by their invariant vectors under the pro-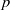$p$ Iwahori subgroup has infinite global dimension (at least if 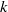$k$ is algebraically closed).

Keywords

pro-p Iwahori–Hecke algebra; Gorenstein ring; cohomological dimension; duality

MSC classification

Secondary: 20C08: Hecke algebras and their representations 16E65: Homological conditions on rings (generalizations of regular, Gorenstein, Cohen-Macaulay rings, etc.) 16E10: Homological dimension
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 13 , Issue 4 , October 2014 , pp. 753 - 809
Copyright
©Cambridge University Press 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajitabh, K., Smith, S. P. and Zhang, J. J., Auslander–Gorenstein rings, Comm. Algebra 26 (7) (1998), 2159–2180.Google Scholar
Auslander, M., On the dimension of modules and algebras. III. Global dimension, Nagoya Math. J. 9 (1955), 67–77.Google Scholar
Bell, A. and Farnsteiner, R., On the theory of Frobenius extensions and its application to Lie superalgebras, Trans. Amer. Math. Soc. 335 (1) (1993), 407–424.Google Scholar
Berg, C., Bergeron, N., Pon, S. and Zabrocki, M., Expansions of $k$-Schur functions in the affine nilCoxeter algebra, 2011 (arXiv:1111.3588v2 [math.CO]).Google Scholar
Bernstein, J. N., Le ‘centre’ de Bernstein, in Representations of reductive groups over a local field (ed. Deligne, P.), Travaux en Cours, pp. 1–32 (Hermann, Paris, 1984).Google Scholar
Borel, A., Admissible representations of a semisimple group with vectors fixed under an Iwahori subgroup, Invent. Math. 35 (1976), 233–259.CrossRefGoogle Scholar
Bornmann, M., Ganzzahlige affine Hecke Algebren. Diplomarbeit, Münster, 2009 (available at www.math.uni-muenster.de/u/schneider/publ/diplom/).Google Scholar
Bourbaki, N., Éléments de mathématiques, in Fascicule XXVII, Algèbre commutative (Hermann, Paris, 1961).Google Scholar
Bourbaki, N., Elements of mathematics, in Lie Groups and Lie Algebras. (Springer, Berlin-Heidelberg-New York, 2002), Chap. 4–6.Google Scholar
Breuil, C., Representations of Galois and of GL2 in characteristic $p$, Lectures at Columbia University, 2004 (available at www.ihes.fr/~breuil/).Google Scholar
Broussous, P., Acyclicity of Schneider and Stuhler’s coefficient systems: another approach on the level 0 case, J. Algebra 279 (2) (2004), 737–748.Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. I. Données radicielles valuées, Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–251.Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local. II. Schémas en groupes. Existence d’une donnée radicielle valuée, Publ. Math. Inst. Hautes Études Sci. 60 (1984), 5–184.CrossRefGoogle Scholar
Buchweitz, R.-O., Maximal Cohen–Macaulay modules and Tate-cohomology over Gorenstein rings, preprint, 1987.Google Scholar
Bushnell, C. J. and Kutzko, P. C., Smooth representations of reductive p-adic groups: structure theory via types, Proc. Lond. Math. Soc. 77 (1998), 582–634.CrossRefGoogle Scholar
Cabanes, M., Extension groups for modular Hecke algebras, J. Fac. Sci. Univ. Tokyo 36 (2) (1989), 347–362.Google Scholar
Carter, R., Finite groups of Lie type. (Wiley Interscience, 1985).Google Scholar
Cartier, P., Representations of $p$-adic groups: a survey, in Automorphic Forms, Representations, and L-Functions (ed. Borel, and Casselmann, ). Proceedings of Symposia in Pure Mathematics, Volume 33(1), pp. 29–69 (American Mathematical Society, 1979).Google Scholar
Chriss, N. and Ginzburg, V., Representation theory and complex geometry. (Birkhäuser Boston, Inc., Boston, MA, 1997).Google Scholar
Enochs, E. and Jenda, O., Relative homological algebra (De Gruyter, Berlin, 2000).Google Scholar
Fayers, M., 0-Hecke algebras of finite Coxeter groups, J. Pure Appl. Algebra 199 (2005), 27–41.CrossRefGoogle Scholar
Heiermann, V., Opérateurs d’entrelacement et algèbres de Hecke avec paramètres d’un groupe réductif $p$-adique: le cas des groupes classiques, Sel. Math. New Ser. 17 (2011), 713–756.Google Scholar
Kazhdan, D. and Lusztig, G., Proof of the Deligne–Langlands conjecture for Hecke algebras, Invent. Math. 87 (1) (1987), 153–215.CrossRefGoogle Scholar
Jantzen, J. C., On the Iwahori–Matsumoto involution and applications, Ann. Sci. Éc. Norm. Supér. 28 (1995), 527–547.Google Scholar
Jantzen, J. C., Representations of Algebraic groups, 2nd edn (American Mathematical Society, 2003).Google Scholar
Kempf, G., Knudson, F., Mumford, D. and Saint-Donat, B., Toroidal Embeddings I, Lecture Notes in Mathematics, Volume 339 (Springer, 1973).Google Scholar
Kirillov, A. and Maeno, T., Affine Nil–Hecke algebras and braided differential structure on affine Weyl groups, Publ. Res. Inst. Math. Sci. 48 (1) (2012), 215–228.CrossRefGoogle Scholar
Lam, T. Y., A first course in noncommutative rings (Springer, Berlin-Heidelberg-New York, 1991).Google Scholar
Lam, T. Y., Lectures on modules and rings (Springer, Berlin-Heidelberg-New York, 1999).CrossRefGoogle Scholar
Lam, T., Affine Stanley symmetric functions, Amer. J. Math. 128 (2006), 1553–1586.Google Scholar
Li, H. and van Oystaeyen, F., Zariskian filtrations (Kluwer, 1996).Google Scholar
Lusztig, G., Affine Hecke algebras and their graded version, J. AMS 2 (3) (1989), 599–635.Google Scholar
McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings. (Wiley-Interscience, 1987).Google Scholar
Ollivier, R., Parabolic Induction and Hecke modules in characteristic $p$ for $p$-adic ${\mathrm{GL} }_{n} $, ANT 4–6 (2010), 701–742.CrossRefGoogle Scholar
Ollivier, R., Le foncteur des invariants sous l’action du pro-$p$-Iwahori de ${\mathrm{GL} }_{2} ({ \mathbb{Q} }_{p} )$, J. Reine Angew. Math. 635 (2009), 149–185.Google Scholar
Ollivier, R. and Sécherre, V., Modules universels de ${\mathrm{GL} }_{3} $ sur un corps $p$-adique en caractéristique $p$, preprint, 2011 (arXiv:1105.2957) (available at www.math.columbia.edu/~ollivier).Google Scholar
Opdam, E. and Solleveld, M., Homological algebra for affine Hecke algebras, Adv. Math. 220 (5) (2009), 1549–1601.Google Scholar
Paškūnas, V., The image of Colmez’s Montréal functor, Publ. Math. IHES, to appear, doi: 10.1007/s10240-013-0049-y.CrossRefGoogle Scholar
Rainwater, J., Global dimension of fully bounded noetherian rings, Commun. Algebra 15 (10) (1987), 2143–2156.Google Scholar
Rogawski, J. D., On modules over the Hecke algebra of a p-adic group, Invent. Math 79 (1985), 443–465.Google Scholar
Sawada, H., Endomorphism rings of split $(B, N)$-pairs, Tokyo J. Math. 1 (1) (1978), 139–148.Google Scholar
Schneider, P., Ausgewählte Kapitel aus der nichtkommutativen Algebra. Lecture Notes, Münster, 2000 (available at www.math.uni-muenster.de/u/schneider/publ/lectnotes/).Google Scholar
Schneider, P. and Stuhler, U., Representation theory and sheaves on the Bruhat–Tits building, Publ. Math. Inst. Hautes Études Sci. 85 (1997), 97–191.Google Scholar
Serre, J.-P., Cohomologie Galoisienne, Lecture Notes in Mathematics, Volume 5 (Springer, 1973).Google Scholar
Stafford, J. T. and Zhang, J. J., Homological properties of (Graded) Noetherian PI Rings, J. Algebra 168 (1994), 988–1026.CrossRefGoogle Scholar
Steinberg, R., Lectures on Chevalley groups, Yale University Notes, 1967.Google Scholar
Tinberg, N. B., Modular representations of finite groups with unsaturated split $(B, N)$-pairs, Canad. J. Math. 32 (3) (1980), 714–733.CrossRefGoogle Scholar
Tits, J., Reductive groups over local fields, in Automorphic Forms, Representations, and L-Functions (ed. Borel, Casselmann) Proceedings of Symposia in Pure Mathematics, Volume 33(1), pp. 29–69 (American Mathematical Society, 1979).CrossRefGoogle Scholar
Vignéras, M.-F., On formal dimensions for reductive $p$-adic groups, in Festschrift in honor of I.I. Piatetski-Shapiro (ed. Gelbart, , Howe, and Sarnak, ) Israel Mathematical Conference Proceedings, Volume 2, pp. 225–266 (Weizmann Science Press, Jerusalem, 1990), Part I.Google Scholar
Vignéras, M.-F., Pro-$p$-Iwahori Hecke ring and supersingular ${ \overline{ \mathbb{F} } }_{p} $-representations, Math. Ann. 331 (2005), 523–556 (erratum: vol. 333(3), p. 699–701).Google Scholar
Vignéras, M.-F., Algèbres de Hecke affines génériques, Represent. Theory 10 (2006), 1–20.CrossRefGoogle Scholar