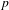 $p$-ADIC VARIATION OF HEEGNER POINTS
$p$-ADIC VARIATION OF HEEGNER POINTSPublished online by Cambridge University Press: 18 February 2019
In this paper, we prove an ‘explicit reciprocity law’ relating Howard’s system of big Heegner points to a two-variable 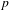 $p$-adic
$p$-adic  $L$-function (constructed here) interpolating the
$L$-function (constructed here) interpolating the 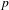 $p$-adic Rankin
$p$-adic Rankin  $L$-series of Bertolini–Darmon–Prasanna in Hida families. As applications, we obtain a direct relation between classical Heegner cycles and the higher weight specializations of big Heegner points, refining earlier work of the author, and prove the vanishing of Selmer groups of CM elliptic curves twisted by 2-dimensional Artin representations in cases predicted by the equivariant Birch and Swinnerton-Dyer conjecture.
$L$-series of Bertolini–Darmon–Prasanna in Hida families. As applications, we obtain a direct relation between classical Heegner cycles and the higher weight specializations of big Heegner points, refining earlier work of the author, and prove the vanishing of Selmer groups of CM elliptic curves twisted by 2-dimensional Artin representations in cases predicted by the equivariant Birch and Swinnerton-Dyer conjecture.
The author was supported in part by NSF grant DMS-1801385. This project received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 682152).