No CrossRef data available.
Article contents
ON THE 
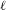$\ell$-ADIC COHOMOLOGY OF SOME 
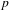$p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
Published online by Cambridge University Press: 01 December 2016
Abstract
We determine the Galois representations inside the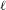 
$\ell$-adic cohomology of some unitary Shimura varieties at split places where they admit uniformization by finite products of Drinfeld upper half spaces. Our main results confirm Langlands–Kottwitz’s description of the cohomology of Shimura varieties in new cases.
MSC classification
Secondary:
14G35: Modular and Shimura varieties
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 5 , November 2018 , pp. 1197 - 1226
- Copyright
- © Cambridge University Press 2016
Footnotes
†
Current address: Morningside Center of Mathematics, No. 55, Zhongguancun East Road, Beijing 100190, China. E-mail: [email protected]
References
Arthur, J. and Clozel, L., Simple Algebras, Base Change, and the Advanced Theory of the Trace Formula, Annals of Mathematics Studies, 120 (Princetion University Press, 1989).Google Scholar
Aubert, A.-M., Baum, P., Plymen, R. and Solleveld, M., The local Langlands correspondence for inner forms of
$SL_{n}$
, preprint, 2013, arXiv:1305.2638.Google Scholar
$SL_{n}$
, preprint, 2013, arXiv:1305.2638.Google ScholarBadulescu, A.-I., Un résultat de transfert et un résultat d’intégrabilité locale des caractères en caractéristique non nulle, J. Reine Angew. Math.
565 (2003), 101–124.Google Scholar
Boutot, J.-F. and Carayol, H., Uniformisation p-adique des courbes de Shimura: Les Théorèmes de Čerednik et de Drinfeld, in Courbes Modulaires et Courbes de Shimura, Astérisque, 196–197, pp. 45–158 (1991).Google Scholar
Boutot, J.-F. and Zink, T., The
$p$
-adic uniformization of Shimura curves, preprint 95-107, Universität Bielefeld (1995), available at https://www.math.uni-bielefeld.de/∼zink/p-adicuni.ps.Google Scholar
$p$
-adic uniformization of Shimura curves, preprint 95-107, Universität Bielefeld (1995), available at https://www.math.uni-bielefeld.de/∼zink/p-adicuni.ps.Google ScholarBoyer, P., Monodromie du faisceau pervers des cycles évanescents de quelques variétés de Shimura simples, Invent. Math.
177 (2009), 239–280.Google Scholar
Carayol, H., Non-abelian Lubin–Tate theory, in Automorphic Forms, Shimura varieties, and L-Functions, Volume 2, Perspectives in Mathematics, 11, pp. 15–39 (Academic Press, 1990).Google Scholar
Dat, J.-F., Théorie de Lubin–Tate non-abélienne et représentations elliptiques, Invent. Math.
169(1) (2007), 75–152.Google Scholar
Deligne, P., Kazhdan, D. and Vignéras, M.-F., Représentations des algèbres centrales simples p-adiques, in Représentations des groupes réductifs sur un corps local, pp. 33–117 (Hermann, Paris, 1984).Google Scholar
Drinfeld, V. G., Coverings of p-adic symmetric domains, Funct. Anal. Appl.
10 (1976), 107–115.Google Scholar
Faltings, G., A relation between two moduli spaces studied by V. G. Drinfeld, in Algebraic Number Theory and Algebraic Geometry, Contemporary Mathematics, 300, pp. 115–129 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Fargues, L., Cohomologie des espaces de modules de groupes p-divisibles et correspondances de Langlands locales, in Variétés de Shimura, espaces de Rapoport–Zink de correspondances de Langlands locales, Astérisque, 291, pp. 1–199 (2004).Google Scholar
Fargues, L., L’isomorphisme entre les tours de Lubin–Tate et de Drinfeld et applications cohomologiques, in L’isomorphisme entre les tours de Lubin–Tate et de Drinfeld, Progress in Mathematics, 262, pp. 1–325 (Birkhäuser, Basel, 2008).Google Scholar
Haines, T. J., The stable Bernstein center and test functions for Shimura varieties, in Automorphic Forms and Galois Representations, Volume 2, London Mathematical Society Lecture Note Series, 415, pp. 118–186 (Cambridge University Press, 2014).Google Scholar
Harris, M., Supercuspidal representations in the cohomology of Drinfel’d upper half spaces; elaboration of Carayol’s program, Invent. Math.
129 (1997), 75–119.Google Scholar
Harris, M., The local Langlands conjecture for GL (n) over a p-adic field, n < p
, Invent. Math.
134(1) (1998), 177–210.Google Scholar
Harris, M., Galois properties of cohomological automorphic forms on GL (n), J. Math. Kyoto Univ.
39(1) (1999), 299–318.Google Scholar
Harris, M. and Taylor, R., The Geometry and Cohomology of Some Simple Shimura Varieties (Princeton University Press, 2001).Google Scholar
Hiraga, K. and Saito, H., On L-packets for inner forms of SL
n
, Mem. Amer. Math. Soc. 1013
215 (2012).Google Scholar
Ito, T., Weight-monodromy conjecture for p-adically uniformized varieties, Invent. Math.
159(3) (2005), 607–656.Google Scholar
Kottwitz, R. E., Rational conjugacy classes in reductive groups, Duke Math. J.
49(4) (1982), 785–806.Google Scholar
Kottwitz, R. E., Shimura varieties and twisted orbital integrals, Math. Ann.
269 (1984), 287–300.Google Scholar
Kottwitz, R. E., Shimura varieties and 𝜆-adic representations, in Automorphic Forms, Shimura Varieties, and L-functions, Volume 1, Perspectives in Mathematics, 10, pp. 161–209 (Academic Press, 1990).Google Scholar
Kottwitz, R. E., On the 𝜆-adic representations associated to some simple Shimura varieties, Invent. Math.
108(3) (1992), 653–665.Google Scholar
Kottwitz, R. E., Points on some Shimura varieties over finite fields, J. Amer. Math. Soc.
5 (1992), 373–444.Google Scholar
Kottwitz, R. E., Isocrystals with additional structure II, Compo. Math.
109(3) (1997), 255–339.Google Scholar
Mantovan, E., On the cohomology of certain PEL-type Shimura varieties, Duke Math.
129 (2005), 573–610.Google Scholar
Mieda, Y., Note on weight-monodromy conjecture for
$p$
-adically uniformized varieties, preprint, 2014, arXiv:1411.5959.Google Scholar
$p$
-adically uniformized varieties, preprint, 2014, arXiv:1411.5959.Google ScholarMilne, J. S., The points on a Shimura variety modulo a prime of good reduction, in The Zeta Functions of Picard Modular Surfaces (ed. Langlands, R. P. and Ramakrishnan, D.), pp. 151–253 (CRM, 1992).Google Scholar
Morel, S., On the Cohomology of Certain Non-compact Shimura Varieties, Annals of Mathematics Studies, 173 (Princeton University Press, 2010).Google Scholar
Rapoport, M., On the local zeta function of quaternionic Shimura varieties with bad reduction, Math. Ann.
279 (1988), 673–697.Google Scholar
Rapoport, M., On the bad reduction of Shimura varieties, in Automorphic Forms, Shimura varieties, and L-Functions, Volume 2, Perspectives in Mathematics, 11, pp. 77–160 (Academic Press, 1990).Google Scholar
Rapoport, M., A guide to reduction modulo p of Shimura varieties, Astérisique
298 (2005), 271–318.Google Scholar
Rapoport, M. and Zink, T., Period Spaces for p-divisible Groups, Annals of Mathematics Studies, 141 (Princetion University Press, 1996).Google Scholar
Reimann, H., The Semi-simple Zeta Function of Quaternionic Shimura Varieties, Lecture Notes in Mathematics, 1657 (Springer, Berlin, 1997).Google Scholar
Rogawski, J., Representations of GL (n) and division algebras over a p-adic field, Duke Math. J.
50 (1983), 161–169.Google Scholar
Scholze, P., The Langlands–Kottwitz approach for some simple Shimura varieties, Invent. Math.
192(3) (2013), 627–661.Google Scholar
Scholze, P., The local Langlands correspondence for GL
n
over p-adic fields, Invent. Math.
192(3) (2013), 663–715.Google Scholar
Scholze, P., The Langlands–Kottwitz method and deformation spaces of p-divisible groups, J. Amer. Math. Soc.
26(1) (2013), 227–259.Google Scholar
Scholze, P. and Shin, S.-W., On the cohomology of compact unitary group Shimura varieties at ramified split places, J. Amer. Math. Soc.
26(1) (2013), 261–294.Google Scholar
Shen, X., On the cohomology of some simple Shimura varieties with bad reduction, preprint, 2014, arXiv:1411.0245.Google Scholar
Shin, S.-W., On the cohomology of Rapoport–Zink spaces of EL type, Amer. J. Math.
134(2) (2012), 407–452.Google Scholar
Varshavsky, Y.,
P-adic uniformization of unitary Shimura varieties, Publ. Math. Inst. Hautes Études Sci.
87 (1998), 57–119.Google Scholar
Varshavsky, Y.,
P-adic uniformization of unitary Shimura varieties II, J. Differential Geom.
49(1) (1998), 75–113.Google Scholar
Varshavsky, Y., Lefschetz–Verdier trace formula and a generalization of a theorem of Fujiwara, Geom. Funct. Anal.
17(1) (2007), 271–319.Google Scholar
Zelevinsky, A., Induced representation of reductive p-adic groups. II. On irreducible representations of GL (n), Ann. Sci. Éc. Norm. Supér. (4)
13(2) (1980), 165–210.Google Scholar