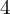Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chan, Stephanie
and
Milovic, Djordjo
2022.
Kuroda’s formula and arithmetic statistics.
Mathematische Zeitschrift,
Vol. 300,
Issue. 2,
p.
1509.
Fouvry, Étienne
Koymans, Peter
and
Pagano, Carlo
2022.
ON THE -RANK OF CLASS GROUPS OF DIRICHLET BIQUADRATIC FIELDS.
Journal of the Institute of Mathematics of Jussieu,
Vol. 21,
Issue. 5,
p.
1543.
Morgan, Adam
and
Paterson, Ross
2022.
On 2‐Selmer groups of twists after quadratic extension.
Journal of the London Mathematical Society,
Vol. 105,
Issue. 2,
p.
1110.
Fouvry, Étienne
and
Koymans, Peter
2023.
On Dirichlet biquadratic fields.
Journal de théorie des nombres de Bordeaux,
Vol. 34,
Issue. 3,
p.
637.
Chan, Stephanie
2024.
The 3-Isogeny Selmer Groups of the Elliptic Curves y2=x3+n2.
International Mathematics Research Notices,
Vol. 2024,
Issue. 9,
p.
7571.
Liu, Yuan
2024.
On the p-Rank of Class Groups of p-Extensions.
International Mathematics Research Notices,
Vol. 2024,
Issue. 6,
p.
5274.