Article contents
ON FORMAL DEGREES OF UNIPOTENT REPRESENTATIONS
Published online by Cambridge University Press: 19 March 2021
Abstract
Let G be a reductive p-adic group which splits over an unramified extension of the ground field. Hiraga, Ichino and Ikeda [24] conjectured that the formal degree of a square-integrable G-representation
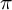 $\pi $
can be expressed in terms of the adjoint
$\pi $
can be expressed in terms of the adjoint
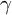 $\gamma $
-factor of the enhanced L-parameter of
$\gamma $
-factor of the enhanced L-parameter of
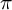 $\pi $
. A similar conjecture was posed for the Plancherel densities of tempered irreducible G-representations.
$\pi $
. A similar conjecture was posed for the Plancherel densities of tempered irreducible G-representations.
We prove these conjectures for unipotent G-representations. We also derive explicit formulas for the involved adjoint
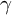 $\gamma $
-factors.
$\gamma $
-factors.
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 6 , November 2022 , pp. 1947 - 1999
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 4
- Cited by



