Published online by Cambridge University Press: 15 July 2022
We propose a conjectural list of Fano manifolds of Picard number 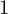 $1$ with pseudoeffective normalised tangent bundles, which we prove in various situations by relating it to the complete divisibility conjecture of Francesco Russo and Fyodor L. Zak on varieties with small codegree. Furthermore, the pseudoeffective thresholds and, hence, the pseudoeffective cones of the projectivised tangent bundles of rational homogeneous spaces of Picard number
$1$ with pseudoeffective normalised tangent bundles, which we prove in various situations by relating it to the complete divisibility conjecture of Francesco Russo and Fyodor L. Zak on varieties with small codegree. Furthermore, the pseudoeffective thresholds and, hence, the pseudoeffective cones of the projectivised tangent bundles of rational homogeneous spaces of Picard number 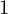 $1$ are explicitly determined by studying the total dual variety of minimal rational tangents (VMRTs) and the geometry of stratified Mukai flops. As a by-product, we obtain sharp vanishing theorems on the global twisted symmetric holomorphic vector fields on rational homogeneous spaces of Picard number
$1$ are explicitly determined by studying the total dual variety of minimal rational tangents (VMRTs) and the geometry of stratified Mukai flops. As a by-product, we obtain sharp vanishing theorems on the global twisted symmetric holomorphic vector fields on rational homogeneous spaces of Picard number 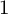 $1$.
$1$.