Published online by Cambridge University Press: 01 July 2015
We investigate questions of maximal symmetry in Banach spaces and the structure of certain bounded non-unitarisable groups on Hilbert space. In particular, we provide structural information about bounded groups with an essentially unique invariant complemented subspace. This is subsequently combined with rigidity results for the unitary representation of 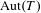 $\text{Aut}(T)$ on
$\text{Aut}(T)$ on 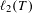 $\ell _{2}(T)$, where
$\ell _{2}(T)$, where  $T$ is the countably infinite regular tree, to describe the possible bounded subgroups of
$T$ is the countably infinite regular tree, to describe the possible bounded subgroups of 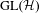 $\text{GL}({\mathcal{H}})$ extending a well-known non-unitarisable representation of
$\text{GL}({\mathcal{H}})$ extending a well-known non-unitarisable representation of 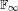 $\mathbb{F}_{\infty }$.
$\mathbb{F}_{\infty }$.
As a related result, we also show that a transitive norm on a separable Banach space must be strictly convex.