Published online by Cambridge University Press: 11 February 2021
We study the metric projection onto the closed convex cone in a real Hilbert space 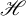 $\mathscr {H}$
generated by a sequence
$\mathscr {H}$
generated by a sequence 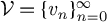 $\mathcal {V} = \{v_n\}_{n=0}^\infty $
. The first main result of this article provides a sufficient condition under which the closed convex cone generated by
$\mathcal {V} = \{v_n\}_{n=0}^\infty $
. The first main result of this article provides a sufficient condition under which the closed convex cone generated by 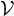 $\mathcal {V}$
coincides with the following set:
$\mathcal {V}$
coincides with the following set: 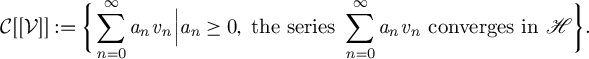
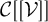 $\mathcal {C}[[\mathcal {V}]]$
. As an application, we obtain the best approximations of many concrete functions in
$\mathcal {C}[[\mathcal {V}]]$
. As an application, we obtain the best approximations of many concrete functions in 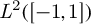 $L^2([-1,1])$
by polynomials with nonnegative coefficients.
$L^2([-1,1])$
by polynomials with nonnegative coefficients.