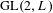Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-04T21:50:59.976Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCALLY ANALYTIC REPRESENTATIONS OF $\text{GL}(2,L)$ VIA SEMISTABLE MODELS OF 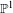$\mathbb{P}^{1}$

Part of: Differential algebra Lie groups Analytic spaces Linear algebraic groups and related topics

Published online by Cambridge University Press:  12 January 2017

Deepam Patel ,
Tobias Schmidt  and
Matthias Strauch
Deepam Patel
Affiliation:
Department of Mathematics, Purdue University, 150 N. University Street, West Lafayette, IN 47907, USA ([email protected])
Tobias Schmidt
Affiliation:
Institut de Recherche Mathématiques de Rennes, Campus Beaulieu, Universite de Rennes 1, 35042 Rennes Cedex, France ([email protected])
Matthias Strauch
Affiliation:
Department of Mathematics, Indiana University, Rawles Hall, Bloomington, IN 47405, USA ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study certain sheaves of 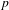$p$-adically complete rings of differential operators on semistable models of the projective line over the ring of integers in a finite extension $L$ of 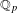$\mathbb{Q}_{p}$. The global sections of these sheaves can be identified with (central reductions of) analytic distribution algebras of wide open congruence subgroups. It is shown that the global sections functor furnishes an equivalence between the categories of coherent module sheaves and finitely presented modules over the distribution algebras. Using the work of M. Emerton, we then describe admissible representations of 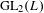$\text{GL}_{2}(L)$ in terms of sheaves on the projective limit of these formal schemes. As an application, we show that representations coming from certain equivariant line bundles on Drinfeld’s first étale covering of the 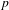$p$-adic upper half plane are admissible.

Keywords

representations of Lie and linear algebraic groups over local fieldsrepresentation theorysheaves of differential operators and their modulesD-modulesrings of differential operators and their modules

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields 20G05: Representation theory 32C38: Sheaves of differential operators and their modules, $D$-modules 13N10: Rings of differential operators and their modules
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 18 , Issue 1 , January 2019 , pp. 125 - 187
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

M. S. would like to acknowledge the support of the National Science Foundation (award DMS-1202303). T. S. would like to acknowledge support of the Heisenberg Programme of Deutsche Forschungsgemeinschaft.

References

Ardakov, K., D̂-modules on rigid analytic spaces, in Proceedings of International Congress of Mathematicians, 2014, Volume III, pp. 1–9 (Kyung Moon Sa co. Ltd., Seoul, Korea).Google Scholar
Ardakov, K. and Wadsley, S., On irreducible representations of compact p-adic analytic groups, Ann. of Math. (2) 178(2) (2013), 453–557.Google Scholar
Beĭlinson, A. and Bernstein, J., Localisation de g-modules, C. R. Acad. Sci. Paris I Math. 292(1) (1981), 15–18.Google Scholar
Berthelot, P., Cohomologie rigide et cohomologie rigide à supports propres (première partie), Preprint. Available at: http://perso.univ-rennes1.fr/pierre.berthelot/.Google Scholar
Berthelot, P., D-modules arithmétiques I. Opérateurs différentiels de niveau fini, Ann. Sci. Éc. Norm. Supér. (4) 29 (1996), 185–272.Google Scholar
Berthelot, P., Cohomologie rigide et théorie des D-modules, in p-Adic Analysis (Trento, 1989), Lecture Notes in Mathematics, Volume 1454, pp. 80–124 (Springer, Berlin, 1990).Google Scholar
Boutot, J.-F. and Carayol, H., Uniformisation p-adique des courbes de Shimura: les théorèmes de Čerednik et de Drinfeld, Astérisque 196–197 (1991), 45–158.Google Scholar
Caro, D., Fonctions L associées aux D-modules arithmétiques. Cas des courbes, Compos. Math. 142(1) (2006), 169–206.Google Scholar
Chiarellotto, B., Duality in rigid analysis, in p-Adic Analysis (Trento, 1989), Lecture Notes in Mathematics, Volume 1454, pp. 142–172 (Springer, Berlin, 1990).Google Scholar
Crew, R., Arithmetic D-modules on a formal curve, Math. Ann. 336(2) (2006), 439–448.Google Scholar
de Jong, A. J., Crystalline Dieudonné module theory via formal and rigid geometry, Publ. Math. Inst. Hautes Études Sci. 82 (1995), 5–96. (1996).Google Scholar
Deligne, P. and Lusztig, G., Representations of reductive groups over finite fields, Ann. of Math. (2) 103(1) (1976), 103–161.Google Scholar
Drinfel’d, V. G., Coverings of p-adic symmetric domains, Funkcional. Anal. i Priložen. 10(2) (1976), 29–40.Google Scholar
Emerton, M., Locally analytic vectors in representations of locally p-adic analytic groups, Mem. AMS. (to appear) Preprint.Google Scholar
Emerton, M., Jacquet modules of locally analytic representations of p-adic reductive groups. I. Construction and first properties, Ann. Sci. Éc. Norm. Supér. (4) 39(5) (2006), 775–839.Google Scholar
Faltings, G., The trace formula and Drinfel’d’s upper halfplane, Duke Math. J. 76(2) (1994), 467–481.Google Scholar
Fresnel, J. and van der Put, M., Rigid Analytic Geometry and its Applications, Progress in Mathematics, Volume 218 (Birkhäuser Boston Inc., Boston, MA, 2004).Google Scholar
Grosse-Klönne, E., On the crystalline cohomology of Deligne–Lusztig varieties, Finite Fields Appl. 13(4) (2007), 896–921.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes, Publ. Math. Inst. Hautes Études Sci. 8 (1961), 222.Google Scholar
Grothendieck, A., Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I, Publ. Math. Inst. Hautes Études Sci. 11 (1961), 167.Google Scholar
Hartshorne, R., Algebraic Geometry, Graduate Texts in Mathematics, Volume 52 (Springer, New York, 1977).Google Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-Modules, Perverse Sheaves, and Representation Theory, Progress in Mathematics, Volume 236, (Birkhäuser Boston Inc., Boston, MA, 2008). Translated from the 1995 Japanese edition by Takeuchi.Google Scholar
Huyghe, C., D† -affinité de l’espace projectif, Compositio Math. 108(3) (1997), 277–318. With an appendix by P. Berthelot.Google Scholar
Huyghe, C., Patel, D., Schmidt, T. and Strauch, M., $\mathscr{D}^{\dagger }$ -affinity of formal models of flag varieties, Preprint, 2015, arXiv:1501.05837.Google Scholar
Kato, K., Logarithmic structures of Fontaine–Illusie, in Algebraic Analysis, Geometry, and Number Theory (Baltimore, MD, 1988), pp. 191–224 (Johns Hopkins University Press, Baltimore, MD, 1989).Google Scholar
Montagnon, C., Généralisation de la théorie arithmétique des $\mathscr{D}$ -modules à la géométrie logarithmique. Thesis, Université de Rennes, 2002, available at: http://tel.archives-ouvertes.fr/tel-00002545/en/.Google Scholar
Noot-Huyghe, C. and Schmidt, T., $D$ -modules arithmétiques, distributions et localisation, Preprint, 2013.Google Scholar
Noot-Huyghe, C. and Trihan, F., Sur l’holonomie de D-modules arithmétiques associés à des F-isocristaux surconvergents sur des courbes lisses, Ann. Fac. Sci. Toulouse Math. (6) 16(3) (2007), 611–634.Google Scholar
Ogus, A., F-isocrystals and de Rham cohomology. II. Convergent isocrystals, Duke Math. J. 51(4) (1984), 765–850.Google Scholar
Ogus, A., The convergent topos in characteristic p , in The Grothendieck Festschrift, Vol. III, Progress in Mathematics, Volume 88, pp. 133–162 (Birkhäuser Boston, Boston, MA, 1990).Google Scholar
Orlik, S., Equivariant vector bundles on Drinfeld’s upper half space, Invent. Math. 172(3) (2008), 585–656.Google Scholar
Orlik, S. and Strauch, M., On Jordan–Hölder series of some locally analytic representations, J. Amer. Math. Soc. 28(1) (2015), 99–157.Google Scholar
Patel, D., Schmidt, T. and Strauch, M., Integral models of ℙ1 and analytic distribution algebras for GL(2), Münster J. Math. 7(1) (2014), 241–271.Google Scholar
Schmidt, T., On locally analytic Beilinson–Bernstein localization and the canonical dimension, Math. Z. 275(3–4) (2013), 793–833.Google Scholar
Schmidt, T. and Strauch, M., Dimensions of some locally analytic representations, Represent. Theory 20 (2016), 14–38.Google Scholar
Schneider, P., Nonarchimedean Functional Analysis, Springer Monographs in Mathematics (Springer, Berlin, 2002).Google Scholar
Schneider, P. and Teitelbaum, J., Locally analytic distributions and p-adic representation theory, with applications to GL2 , J. Amer. Math. Soc. 15(2) (2002), 443–468. (electronic).Google Scholar
Schneider, P. and Teitelbaum, J., Algebras of p-adic distributions and admissible representations, Invent. Math. 153(1) (2003), 145–196.Google Scholar
Shiho, A., Relative log convergent cohomology and relative rigid cohomology I, Preprint, 2008, arXiv:0707.1742.Google Scholar
Shiho, A., Crystalline fundamental groups. II. Log convergent cohomology and rigid cohomology, J. Math. Sci. Univ. Tokyo 9(1) (2002), 1–163.Google Scholar
Teitelbaum, J., On Drinfel’d’s universal formal group over the p-adic upper half plane, Math. Ann. 284(4) (1989), 647–674.Google Scholar
Teitelbaum, J., Geometry of an étale covering of the p-adic upper half plane, Ann. Inst. Fourier (Grenoble) 40(1) (1990), 68–78.Google Scholar
Tsuzuki, N., On base change theorem and coherence in rigid cohomology, Doc. Math. (Extra Vol.) (2003), 891–918. (electronic). Kazuya Kato’s fiftieth birthday.Google Scholar