Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-25T07:14:27.513Z Has data issue: false hasContentIssue false
  • English
  • Français

LIE ALGEBROIDS AS 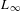$L_{\infty }$ SPACES

Part of: Families, fibrations Pseudogroups, differentiable groupoids and general structures on manifolds Symplectic geometry, contact geometry

Published online by Cambridge University Press:  13 February 2018

Ryan Grady Open the ORCID record for Ryan Grady [Opens in a new window]  and
Owen Gwilliam
Ryan Grady
Affiliation:
Department of Mathematical Sciences, Montana State University, Bozeman, MT 59717, USA ([email protected])
Owen Gwilliam
Affiliation:
Max Planck Institut für Mathematik, Vivatsgasse 7, 53111 Bonn, Germany ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we relate Lie algebroids to Costello’s version of derived geometry. For instance, we show that each Lie algebroid – and the natural generalization to dg Lie algebroids – provides an (essentially unique) 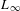$L_{\infty }$ space. More precisely, we construct a faithful functor from the category of Lie algebroids to the category of 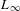$L_{\infty }$ spaces. Then we show that for each Lie algebroid $L$, there is a fully faithful functor from the category of representations up to homotopy of $L$ to the category of vector bundles over the associated 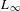$L_{\infty }$ space. Indeed, this functor sends the adjoint complex of $L$ to the tangent bundle of the 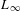$L_{\infty }$ space. Finally, we show that a shifted symplectic structure on a dg Lie algebroid produces a shifted symplectic structure on the associated 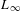$L_{\infty }$ space.

Keywords

dg Lie algebroidderived geometryshifted symplectic structure

MSC classification

Primary: 58H15: Deformations of structures 53D17: Poisson manifolds; Poisson groupoids and algebroids 14D23: Stacks and moduli problems
Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 19 , Issue 2 , March 2020 , pp. 487 - 535
Copyright
© Cambridge University Press 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partially supported by the National Science Foundation under Award DMS-1309118. The second author was partially supported as a postdoctoral fellow by the National Science Foundation under Award DMS-1204826.

References

Abad, C. A. and Crainic, M., The Weil algebra and the Van Est isomorphism, Ann. Inst. Fourier (Grenoble) 61(3) (2011), 927–970.Google Scholar
Abad, C. A. and Crainic, M., Representations up to homotopy of Lie algebroids, J. Reine Angew. Math. 663 (2012), 91–126.Google Scholar
Abad, C. A. and Crainic, M., Representations up to homotopy and Bott’s spectral sequence for Lie groupoids, Adv. Math. 248 (2013), 416–452.Google Scholar
Alexandrov, M., Schwarz, A., Zaboronsky, O. and Kontsevich, M., The geometry of the master equation and topological quantum field theory, Internat. J. Modern Phys. A 12(7) (1997), 1405–1429.Google Scholar
Ben-Bassat, O., Brav, C., Bussi, V. and Joyce, D., A ‘Darboux theorem’ for shifted symplectic structures on derived Artin stacks, with applications, Geom. Topol. 19(3) 1287–1359.Google Scholar
Berger, C. and Moerdijk, I., On the derived category of an algebra over an operad, Georgian Math. J. 16(1) (2009), 13–28.Google Scholar
Bonavolontà, G. and Poncin, N., On the category of Lie n-algebroids, J. Geom. Phys. 73 (2013), 70–90.Google Scholar
Bouaziz, E. and Grojnowski, I., A d-shifted Darboux theorem, Preprint, 2013,arXiv:1309.2197.Google Scholar
Calaque, D., Căldăraru, A. and Tu, J., On the Lie algebroid of a derived self-intersection, Adv. Math. 262 (2014), 751–783.Google Scholar
Calaque, D., Dolgushev, V. and Halbout, G., Formality theorems for Hochschild chains in the Lie algebroid setting, J. Reine Angew. Math. 612 (2007), 81–127.Google Scholar
Calaque, D., Pantev, T., Toën, B., Vaquié, M. and Vezzosi, G., Shifted Poisson structures and deformation quantization, J. Topol. 10(2) (2017), 483–584.Google Scholar
Calaque, D., Rossi, C. A. and van den Bergh, M., Hochschild (co)homology for Lie algebroids, Int. Math. Res. Not. IMRN 21 (2010), 4098–4136.Google Scholar
Cattaneo, A. S., Felder, G. and Tomassini, L., From local to global deformation quantization of Poisson manifolds, Duke Math. J. 115(2) (2002), 329–352.Google Scholar
Cattaneo, A. S. and Mnëv, P., Remarks on Chern–Simons invariants, Comm. Math. Phys. 293(3) (2010), 803–836.Google Scholar
Cattaneo, A. S. and Schätz, F., Introduction to supergeometry, Rev. Math. Phys. 23(6) (2011), 669–690.Google Scholar
Chan, K., Leung, N. C. and Li, Q., BV quantization of the Rozansky–Witten model, Comm. Math. Phys. 355(1) (2017), 97–144.Google Scholar
Costello, K., A geometric construction of the Witten genus, II, Preprint, 2011,arXiv:1112.0816.Google Scholar
Costello, K., Renormalization and Effective Field Theory, Mathematical Surveys and Monographs, Volume 170 (American Mathematical Society, Providence, RI, 2011).Google Scholar
Crainic, M. and Fernandes, R. L., Integrability of Lie brackets, Ann. of Math. (2) 157(2) (2003), 575–620.Google Scholar
Crainic, M. and Moerdijk, I., Deformations of Lie brackets: cohomological aspects, J. Eur. Math. Soc. (JEMS) 10(4) (2008), 1037–1059.Google Scholar
da Silva, A. C. and Weinstein, A., Geometric Models for Noncommutative Algebras, Berkeley Mathematics Lecture Notes, Volume 10 (American Mathematical Society, Providence, RI, 1999). Berkeley Center for Pure and Applied Mathematics, Berkeley, CA.Google Scholar
Evens, S., Lu, J.-H. and Weinstein, A., Transverse measures, the modular class and a cohomology pairing for Lie algebroids, Q. J. Math. Oxford Ser. (2) 50(200) (1999), 417–436.Google Scholar
Fedosov, B. V., A simple geometrical construction of deformation quantization, J. Differential Geom. 40(2) (1994), 213–238.Google Scholar
Fernandes, R. L., Lie algebroids, holonomy and characteristic classes, Adv. Math. 170(1) (2002), 119–179.Google Scholar
Friedan, D. H., Nonlinear models in 2+𝜀 dimensions, Ann. Physics 163(2) (1985), 318–419.Google Scholar
Gaitsgory, D. and Rozenblyum, N., A study in derived algebraic geometry, in Deformations, Lie Theory and Formal Geometry, Vol. II, Mathematical Surveys and Monographs, Volume 221 (American Mathematical Society, Providence, RI, 2017).Google Scholar
Gorbounov, V., Gwilliam, O. and Williams, B., Chiral differential operators via Batalin–Vilkovisky quantization, Preprint, 2016, arXiv:1610.09657.Google Scholar
Gracia-Saz, A. and Mehta, R. A., Lie algebroid structures on double vector bundles and representation theory of Lie algebroids, Adv. Math. 223(4) (2010), 1236–1275.Google Scholar
Grady, R. and Gwilliam, O., One-dimensional Chern–Simons theory and the  genus, Algebr. Geom. Topol. 14(4) (2014), 419–497.Google Scholar
Grady, R. and Gwilliam, O., L ∞ spaces and derived loop spaces, New York J. Math. 21 (2015), 231–272.Google Scholar
Grady, R., Gwilliam, O. and Williams, B., Topological mechanics on a twisted cotangent bundle, forthcoming, 2018.Google Scholar
Grady, R. E., Li, Q. and Li, S., Batalin–Vilkovisky quantization and the algebraic index, Adv. Math. 317 (2017), 575–639.Google Scholar
Grady, R. and Williams, B., Homotopy RG flow and the nonlinear $\unicode[STIX]{x1D70E}$-model, Preprint, 2017, arXiv:1710.05973.Google Scholar
Hennion, B., Tangent Lie algebra of derived Artin stacks, Crelle, doi:10.1515/crelle-2015-0065.Google Scholar
Hinich, V., DG coalgebras as formal stacks, J. Pure Appl. Algebra 162(2–3) (2001), 209–250.Google Scholar
Ikeda, N., Chern–Simons gauge theory coupled with BF theory, Internat. J. Modern Phys. A 18(15) (2003), 2689–2701.Google Scholar
Kalkman, J., BRST model for equivariant cohomology and representatives for the equivariant Thom class, Comm. Math. Phys. 153(3) (1993), 447–463.Google Scholar
Kapranov, M., Rozansky–Witten invariants via Atiyah classes, Compos. Math. 115(1) (1999), 71–113.Google Scholar
Kjeseth, L., Homotopy Rinehart cohomology of homotopy Lie–Rinehart pairs, Homology, Homotopy Appl. 3(1) (2001), 139–163.Google Scholar
Kotov, A. and Strobl, T., Generalizing geometry – algebroids and sigma models, in Handbook of Pseudo-Riemannian Geometry and Supersymmetry, IRMA Lectures in Mathematics and Theoretical Physics, Volume 16, pp. 209–262 (Eur. Math. Soc., Zürich, 2010).Google Scholar
Li, Q. and Li, S., On the B-twisted topological sigma model and Calabi–Yau geometry, J. Differential Geom. 102(3) (2016), 409–484.Google Scholar
Lurie, J., Derived Algebraic Geometry X: Formal Moduli Problems. 2011, author’s homepage, http://www.math.harvard.edu/∼lurie/.Google Scholar
Mackenzie, K. C. H., General theory of Lie groupoids and Lie algebroids, London Mathematical Society Lecture Note Series, Volume 213 (Cambridge University Press, Cambridge, 2005).Google Scholar
Mac Lane, S., Categories for the Working Mathematician, second edition, Graduate Texts in Mathematics, Volume 5 (Springer, New York, 1998).Google Scholar
Manetti, M., Differential graded Lie algebras and formal deformation theory, in Algebraic Geometry—Seattle 2005, Proceedings of Symposia in Pure Mathematics, Part 2, Volume 80, pp. 785–810 (American Mathematical Society, Providence, RI, 2009).Google Scholar
Mayer, C. and Strobl, T., Lie algebroid Yang–Mills with matter fields, J. Geom. Phys. 59(12) (2009), 1613–1623.Google Scholar
Mehta, R. A., Lie algebroid modules and representations up to homotopy, Indag. Math. (N.S.) 25(5) (2014), 1122–1134.Google Scholar
Nest, R. and Tsygan, B., Algebraic index theorem, Comm. Math. Phys. 172(2) (1995), 223–262.Google Scholar
Nguyen, T., Quantization of the nonlinear sigma model revisited, J. Math. Phys. 57(8) (2016), 082301. 40.Google Scholar
Oh, Y.-G. and Park, J.-S., Deformations of coisotropic submanifolds and strong homotopy Lie algebroids, Invent. Math. 161(2) (2005), 287–360.Google Scholar
Pantev, T., Toën, B., Vaquié, M. and Vezzosi, G., Shifted symplectic structures, Publ. Math. Inst. Hautes Études Sci. 117 (2013), 271–328.Google Scholar
Pym, B. and Safronov, P., Shifted symplectic Lie algebroids, Preprint, 2016,arXiv:1612.09446.Google Scholar
Rinehart, G. S., Differential forms on general commutative algebras, Trans. Amer. Math. Soc. 108 (1963), 195–222.Google Scholar
Roytenberg, D., On the structure of graded symplectic supermanifolds and Courant algebroids, in Quantization, Poisson Brackets and Beyond (Manchester, 2001), Contemporary Mathematics, Volume 315, pp. 169–185 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Roytenberg, D., AKSZ-BV formalism and Courant algebroid-induced topological field theories, Lett. Math. Phys. 79(2) (2007), 143–159.Google Scholar
Sati, H., Schreiber, U. and Stasheff, J., Twisted differential string and fivebrane structures, Comm. Math. Phys. 315(1) (2012), 169–213.Google Scholar
Ševera, P., Some title containing the words ‘homotopy’ and ‘symplectic’, e.g. this one, in Travaux mathématiques. Fasc. XVI, Travaux Mathématiques, Volume XVI, pp. 121–137 (Univ. Luxemb., Luxembourg, 2005).Google Scholar
Ševera, P. and Weinstein, A., Poisson geometry with a 3-form background, Progr. Theoret. Phys. Suppl. 144 (2001), 145–154. Noncommutative geometry and string theory (Yokohama, 2001).Google Scholar
Strobl, T., Algebroid Yang–Mills theories, Phys. Rev. Lett. 93(21) (2004), 211601. 4.Google Scholar
Vaĭntrob, A. Y., Lie algebroids and homological vector fields, Uspekhi Mat. Nauk 52(2(314)) (1997), 161–162.Google Scholar
Vezzosi, G., A model structure on relative dg-Lie algebroids, in Stacks and categories in geometry, topology, and algebra, Contemporary Mathematics, Volume 643, pp. 111–118 (American Mathematical Society, Providence, RI, 2015).Google Scholar
Vitagliano, L., Representations of homotopy Lie–Rinehart algebras, Math. Proc. Cambridge Philos. Soc. 158(1) (2015), 155–191.Google Scholar