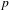 $p$-CLASS TOWERS OF REAL QUADRATIC FIELDS
$p$-CLASS TOWERS OF REAL QUADRATIC FIELDSPublished online by Cambridge University Press: 26 December 2019
Let 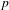 $p$ be an odd prime. For a number field
$p$ be an odd prime. For a number field 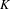 $K$, we let
$K$, we let 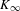 $K_{\infty }$ be the maximal unramified pro-
$K_{\infty }$ be the maximal unramified pro-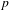 $p$ extension of
$p$ extension of 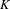 $K$; we call the group
$K$; we call the group 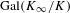 $\text{Gal}(K_{\infty }/K)$ the
$\text{Gal}(K_{\infty }/K)$ the 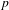 $p$-class tower group of
$p$-class tower group of 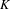 $K$. In a previous work, as a non-abelian generalization of the work of Cohen and Lenstra on ideal class groups, we studied how likely it is that a given finite
$K$. In a previous work, as a non-abelian generalization of the work of Cohen and Lenstra on ideal class groups, we studied how likely it is that a given finite 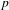 $p$-group occurs as the
$p$-group occurs as the 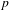 $p$-class tower group of an imaginary quadratic field. Here we do the same for an arbitrary real quadratic field
$p$-class tower group of an imaginary quadratic field. Here we do the same for an arbitrary real quadratic field 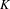 $K$ as base. As before, the action of
$K$ as base. As before, the action of 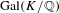 $\text{Gal}(K/\mathbb{Q})$ on the
$\text{Gal}(K/\mathbb{Q})$ on the 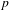 $p$-class tower group of
$p$-class tower group of 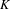 $K$ plays a crucial role; however, the presence of units of infinite order in the ground field significantly complicates the possibilities for the groups that can occur. We also sharpen our results in the imaginary quadratic field case by removing a certain hypothesis, using ideas of Boston and Wood. In the appendix, we show how the probabilities introduced for finite
$K$ plays a crucial role; however, the presence of units of infinite order in the ground field significantly complicates the possibilities for the groups that can occur. We also sharpen our results in the imaginary quadratic field case by removing a certain hypothesis, using ideas of Boston and Wood. In the appendix, we show how the probabilities introduced for finite 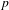 $p$-groups can be extended in a consistent way to the infinite pro-
$p$-groups can be extended in a consistent way to the infinite pro-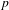 $p$ groups which can arise in both the real and imaginary quadratic settings.
$p$ groups which can arise in both the real and imaginary quadratic settings.
The research of NB is supported by Simons grant MSN179747. The work of MRB was partially supported by summer Lenfest Grants from Washington and Lee University.