Article contents
GYSIN TRIANGLES IN THE CATEGORY OF MOTIFS WITH MODULUS
Published online by Cambridge University Press: 06 January 2022
Abstract
In this article, we study a Gysin triangle in the category of motives with modulus (Theorem 1.2). We can understand this Gysin triangle as a motivic lift of the Gysin triangle of log-crystalline cohomology due to Nakkajima and Shiho. After that we compare motives with modulus and Voevodsky motives (Corollary 1.6). The corollary implies that an object in 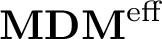 $\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$ decomposes into a p-torsion part and a Voevodsky motive part. We can understand the corollary as a motivic analogue of the relationship between rigid cohomology and log-crystalline cohomology.
$\operatorname {\mathbf {MDM}^{\operatorname {eff}}}$ decomposes into a p-torsion part and a Voevodsky motive part. We can understand the corollary as a motivic analogue of the relationship between rigid cohomology and log-crystalline cohomology.
Keywords
MSC classification
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 22 , Issue 5 , September 2023 , pp. 2131 - 2154
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by



