Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Charles, François
2014.
On the Picard number of K3 surfaces over number fields.
Algebra & Number Theory,
Vol. 8,
Issue. 1,
p.
1.
Ieronymou, Evis
and
Skorobogatov, Alexei N.
2015.
Odd order Brauer–Manin obstruction on diagonal quartic surfaces.
Advances in Mathematics,
Vol. 270,
Issue. ,
p.
181.
Creutz, Brendan
and
Viray, Bianca
2015.
On Brauer groups of double covers of ruled surfaces.
Mathematische Annalen,
Vol. 362,
Issue. 3-4,
p.
1169.
Várilly-Alvarado, Anthony
2017.
Geometry Over Nonclosed Fields.
p.
197.
Iliev, Atanas
Kapustka, Grzegorz
Kapustka, Michał
and
Ranestad, Kristian
2017.
Hyper-Kähler fourfolds and Kummer surfaces.
Proceedings of the London Mathematical Society,
Vol. 115,
Issue. 6,
p.
1276.
Cantoral‐Farfán, Victoria
Tang, Yunqing
Tanimoto, Sho
and
Visse, Erik
2018.
Effective bounds for Brauer groups of Kummer surfaces over number fields.
Journal of the London Mathematical Society,
Vol. 97,
Issue. 3,
p.
353.
Balestrieri, F.
2018.
Iterating the algebraic étale-Brauer set.
Journal of Number Theory,
Vol. 182,
Issue. ,
p.
284.
Corn, Patrick
and
Nakahara, Masahiro
2018.
Brauer–Manin obstructions on degree 2 K3 surfaces.
Research in Number Theory,
Vol. 4,
Issue. 3,
Hassett, Brendan
and
Tschinkel, Yuri
2019.
On stable rationality of Fano threefolds and del Pezzo fibrations.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2019,
Issue. 751,
p.
275.
Frei, Sarah
2020.
Moduli spaces of sheaves on K3 surfaces and Galois representations.
Selecta Mathematica,
Vol. 26,
Issue. 1,
Addington, Nicolas
Antieau, Benjamin
Honigs, Katrina
and
Frei, Sarah
2021.
Rational points and derived equivalence.
Compositio Mathematica,
Vol. 157,
Issue. 5,
p.
1036.
Hashimoto, Sachi
Honigs, Katrina
Lamarche, Alicia
Vogt, Isabel
and
Addington, Nicolas
2022.
A transcendental Brauer–Manin obstruction to weak approximation on a Calabi–Yau threefold.
Research in Number Theory,
Vol. 8,
Issue. 1,
Pagano, Margherita
2022.
An example of a Brauer–Manin obstruction to weak approximation at a prime with good reduction.
Research in Number Theory,
Vol. 8,
Issue. 3,
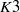 $K 3$ surfaces
$K 3$ surfaces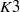 $K 3$ surface
$K 3$ surface 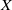 $X$ of degree
$X$ of degree 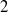 $2$ over
$2$ over 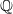 $ \mathbb{Q} $, together with a 2-torsion Brauer class
$ \mathbb{Q} $, together with a 2-torsion Brauer class  $\alpha $ that is unramified at every finite prime, but ramifies at real points of
$\alpha $ that is unramified at every finite prime, but ramifies at real points of 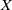 $X$. With motivation from Hodge theory, the pair
$X$. With motivation from Hodge theory, the pair 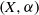 $(X, \alpha )$ is constructed from a double cover of
$(X, \alpha )$ is constructed from a double cover of 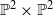 ${ \mathbb{P} }^{2} \times { \mathbb{P} }^{2} $ ramified over a hypersurface of bidegree
${ \mathbb{P} }^{2} \times { \mathbb{P} }^{2} $ ramified over a hypersurface of bidegree 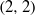 $(2, 2)$.
$(2, 2)$.